Сфера Пуанкаре

1. Энергетические характеристики

• Вектор Пойнтинга S - плотность потока энергии
электромагнитного поля (непрерывен на границе двух сред)
Закон
преобразования энергии
• Интенсивность I = <ISI> - усреднение по времени
• Плотность импульса p = S/c2 (давление света)
• Угловой момент r х S/c (для неплоских фронтов, кручение)
Используется для атомарных ловушек, манипуляции отдельными атомами,
получение сверхнизких температур.

2. Волновое уравнение (ещё один вариант)

Однородная среда
c- диэлектрическая восприимчивость
Неоднородная среда
e и c- зависят от координаты
1
n 2 r 2 E
n 2 r 2 E
2
2
E 2 n r E - 2 2 0 E - 2 2 0
c0
t
c0
t
n r
2
Приближение для медленных изменений n(r), незначительных на расстоянии порядка длины волны
Компоненты электрического и магнитного полей описываются одинаковыми
скалярными волновыми уравнениями

3. Комплексные амплитуды

Комплексный вектор Пойнтинга

4. Плоские волны

• E0, H0 – комплексные амплитуды (постоянные вектора)
• k– волновой вектор
• E и H – перпендикулярны направлению распространения
Поперечная электромагнитная волна (TEM) образует правую
тройку векторов (E0,H0, k)
Интенсивность 10 W/cm2 соответствует ~ 87 V/cm

5. Элементарные волны

Сферические волны
Волновой фронт сферический,
E, H – ортогональны друг другу
и радиальному направлению.
В общем случае амплитуда изменяется с углом
Параксиальное приближение
Излучение электрического диполя (волновая – дальняя зона)
E~
Решение уравнений Максвелла в сферической системе координат

6. Элементарные волны

Гауссов пучок

7. Поляризация

Поляризация света определяется направлением вектора
электрического поля E (r,t)
1.
В изотропной однородной среде вектор E лежит в плоскости
касательной к волновому фронту
2.
Для монохроматической волны любые ортогональные
компоненты E в тангенциальной плоскости изменяются
гармонически со временем
3.
Амплитуда и фаза этих составляющих определяет траекторию
движения вектора E (в общем случае эллипс)

8. Поляризация

Для плоской волны эта траектория не изменяется в
пространстве. Говорят об линейной, циркулярной или
эллиптической поляризации
Поляризация играет важную роль при взаимодействии света с
веществом:
Отражение и преломление
Поглощение
Анизотропия
1.

9. Поляризация

Эллиптическая поляризация
Параметрическое уравнение для компонент электрического поля
ax
r
ay
x - y
При фиксированном z вектор E вращается с
частотой w и разностью фаз
ax2 a y2
I
2

10. Поляризация

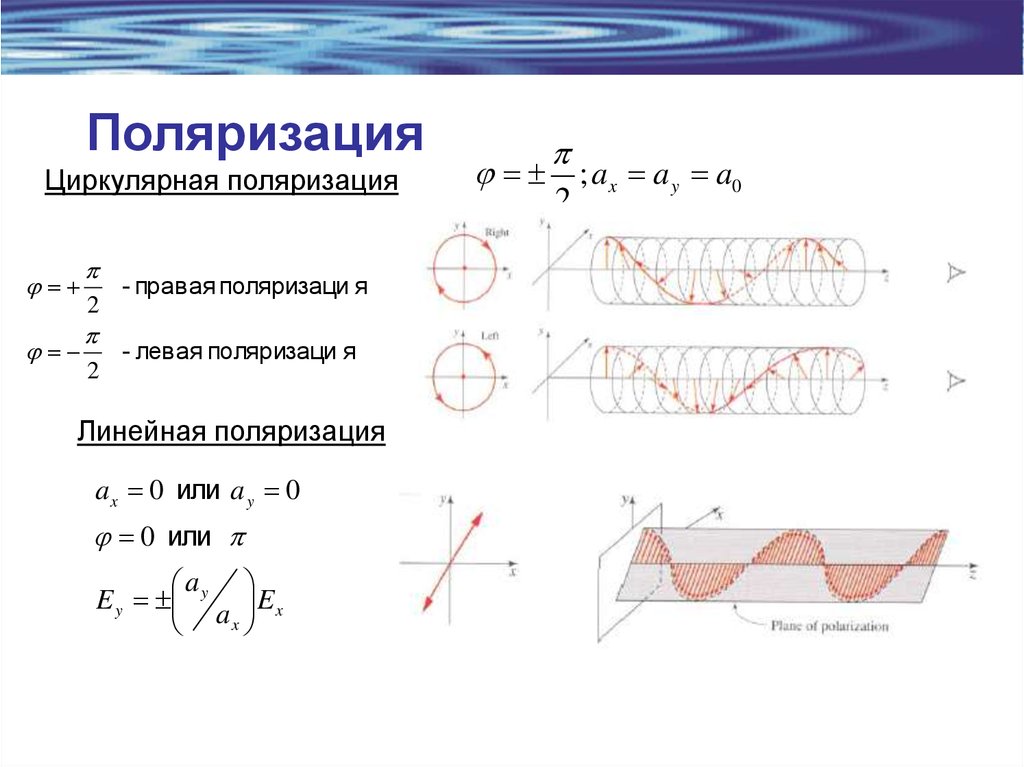
Циркулярная поляризация
-
2
2
- правая поляризаци я
- левая поляризаци я
Линейная поляризация
a x 0 или a y 0
0 или
a
E y y E x
ax
; a x a y a0
2

11. Поляризация математическое описание

Сфера Пуанкаре
Состоянию поляризации соответствует точка на поверхности сферы
(r=1, q=90o– 2c, f = 2Y)

12. Поляризация математическое описание

Параметры Стокса
(S0, S1, S2, S3)
S 0 a x2 ay2 I
( S1 , S 2 , S3 ) S 0 cos 2 c cos 2 , cos 2 c sin 2 , sin 2 c
- Декартовые координаты тточк на сфере
S 12 S 22 S 32 S 02 - 3 независимых параметра

13. Поляризация математическое описание

Матричное описание
Монохроматическая плоская волна может быть описана вектором
из двух компонент (Ax, Ay)
Вектор Джонса
Ортогональные поляризации:
Произвольная поляризация описывается как суперпозиция ортогональных
векторов (базиса)

14. Распространение поляризованного света через линейную оптическую систему

Поляризатор
Волновые пластики

15. Распространение поляризованного света через линейную оптическую систему

Волновые пластики

16. Сложная система

Иногда удобно сменить систему координат
Собственные вектора поляризации не меняются при распространении и
образуют базис для разложения произвольной поляризации
Для матрицы 2Х2 существуют две собственные моды

17. Неполяризованный свет

Строгое математическое описание поляризации дается
статистической теорией когерентности.
!!! Неполяризованный свет – случайные фазовые соотношения
между компонентами (не может быть описан вектором Джонса)
Степень поляризации