Similar presentations:
Числовая последовательность
1.
§4. Числоваяпоследовательность
п.1. Кванторы.
─ квантор существования («существует»)
─ квантор общности («для любого»)
2.
Окрестностью точки называется любойинтервал, содержащий эту точку.
x
- окрестностью точки a называется
интервал ( a ; a ).
a
a
a
x
3.
п.2. Основные понятия.Числовой последовательностью
называется правило, согласно которому
каждому натуральному числу n поставлено в
соответствие действительное число xn.
Обозначение:
{xn },
x n , n N.
4.
Примеры.1)
2, 4, 6, ?8, …
2)
xn ( 1) 2
n
n
x1 ( 1) 2 2
1
1
x2 ( 1) 2 4
x3 ? 8
2
2
5.
Последовательность { xn } называетсяограниченной, если
M 0 n N : | xn | M
Геометрическая интерпретация
M xn
x3
x1 x2
M
x
6.
Пример.2
xn 1
n
1
1
2
x4
M 1
1
3
0
x3 x2
x1 1?
x2 ?0
1
x3 ?
3
1
x4 ?
2
1
x1
Самостоятельно: привести еще 2 примера.
x
7.
Последовательность { xn } называетсянеограниченной, если
M 0 n N : | xn | M
Пример.
xn n
M 100
M 1000
2
n 11, x11 121
n 32, x32 1024
Самостоятельно: привести еще 2 примера.
8.
Последовательностьпостоянной, если
{xn } называется
n N : xn a, a const .
Пример.
xn 2
x1 2,
x2 2,...
9.
Последовательность { xn } называетсявозрастающей, если
n N :
n
Пример. xn
,
2
xn xn 1.
[x ] ─ целая часть x.
0,
0,1,1,2,2,3,3,…
0,1,1,?
0,1,?
Самостоятельно: привести еще 2 примера.
10.
Последовательностьубывающей, если
n N :
{xn } называется
xn xn 1.
100
Пример. xn
.
n
Самостоятельно: привести еще 2 примера.
Возрастающие
Убывающие
Монотонные последовательности
11.
Последовательность{xn } называется
строго возрастающей, если
n N :
Пример.
xn xn 1.
xn n .
2
Последовательность
{xn } называется
строго убывающей, если
n N :
xn xn 1.
Пример. xn n.
Самостоятельно: привести еще по 2 примера.
12.
Строго возрастающиеСтрого убывающие
Строго монотонные последовательности
Самостоятельно: привести 2 примера
последовательностей, не являющихся
монотонными.
13.
п.3. Предел числовой последовательности.n 1
Пример. xn
.
n
x1
x2
x3 x4
x
2 3
1
3 4
1
1
1
x1 1 1, x2 1 , x3 1 , x4 1 ,...
4
2
3
0
xn 1 ?0
1
2
xn 1?
14.
Число a называется пределомпоследовательности {xn }, если
для любого действительного числа
можно указать такое натуральное число N0,
что для всех элементов последовательности с
номерами большими, чем N0, будет
выполняться неравенство
xn a .
lim xn a 0 N 0 N : n N 0
n
xn a
15.
Примеры.n 1
lim
1;
n n
n 1
lim 2 n 2.
n
16.
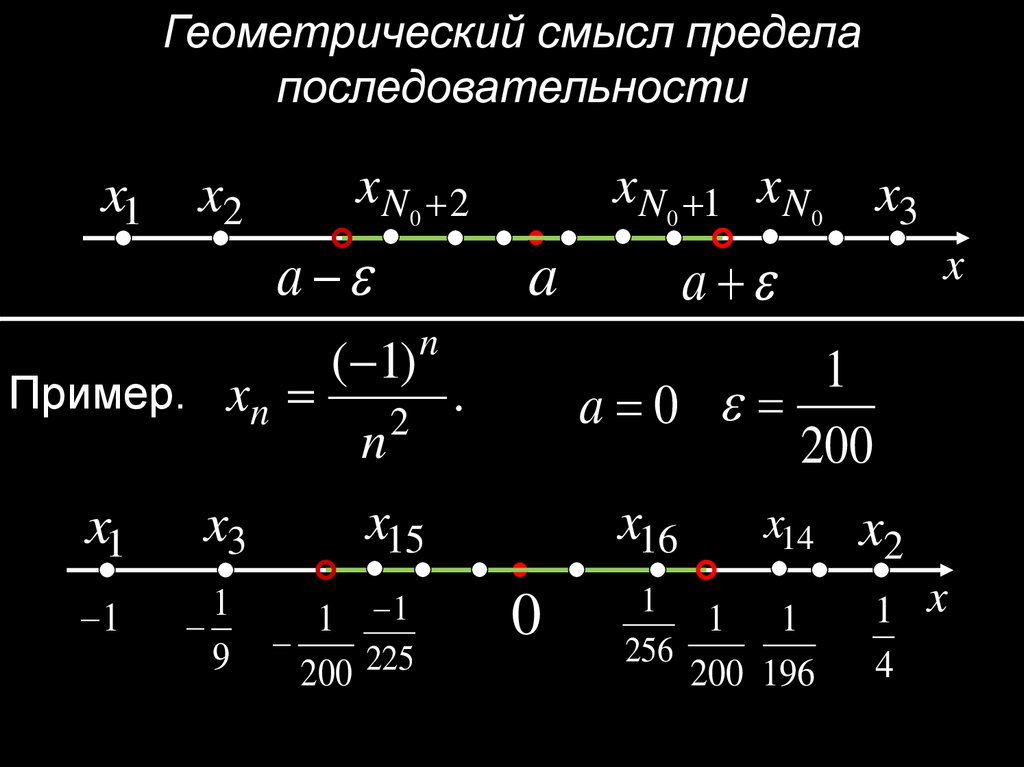
Геометрический смысл пределапоследовательности
x1
x2
xN0 2
a
Пример. xn
a
( 1)
n
x N0 1 x N 0 x3
n
2
x1
x3
x15
1
1
9
1 1
200 225
a
x
1
a 0
200
x14 x2
x16
.
0
1
1
256
1
200 196
1 x
4
17.
Последовательность{xn } называется
бесконечно малой (БМП), если
0 N 0 N : n N 0
lim xn 0
xn
n
1
Пример. xn .
n
Самостоятельно: привести еще 2 примера.
18.
Свойства БМП1. Сумма двух БМП есть БМП.
Доказательство.
{xn } ─ БМП
{ yn } ─ БМП
{ xn y n } ─ БМП ?
19.
0{xn } ─ БМП
2
0
N1 N : n N1
{ yn } ─ БМП
2
0
N 2 N : n N 2
xn
2
yn
2
20.
N 0 max{ N1 , N 2 }n N 0
xn y n xn y n
2 2
0 N 0 N : n N 0 xn yn
{ xn y n } ─ БМП
21.
2. БМП ─ ограниченная последовательность.3. Произведение двух БМП есть БМП.
4. Произведение БМП и ограниченной
последовательности есть БМП.
22.
Последовательность{xn } называется
бесконечно большой (ББП), если
A 0 N 0 N : n N 0
xn A
lim xn lim xn , lim xn
n
n
n
Примеры. xn ln n;
xn n .
Самостоятельно: привести еще 2 примера.
23.
Свойства ББП1.ББП ─ неограниченная последовательность.
2. Произведение двух ББП есть ББП.
3. Сумма ББП и ограниченной
последовательности есть ББП.
24.
Замечание 1. Сумма двух ББП не обязательноявляется ББП.
Пример.
x n n,
yn n.
xn y n 0.
25.
Связь между БМП и ББПТеорема 1. Если { xn } ─ ББП и n N xn 0,
1
то ─ БМП.
xn
Обратно, если { xn } ─ БМП и n N xn 0,
1
то ─ ББП.
xn
Самостоятельно: проиллюстрировать теорему
на двух примерах.
26.
Замечание 2.1) Если lim xn a , то говорят, что
n
{xn } сходится к числу a; {xn } ─ сходящаяся.
2) Если lim xn , то говорят, что
n
{xn } сходится к .
3) Если{ xn }не имеет предела, то говорят, что
{xn } расходится.
Пример. xn ( 1) : 1, 1, 1, 1, ....
n
27.
п.4. Свойства сходящихсяпоследовательностей.
1. Для того, чтобы последовательность { xn }
имела своим пределом число a, необходимо и
достаточно, чтобы последовательность { xбыла
n a}
БМП.
lim xn a {xn a} ─ БМП
n
Доказательство самостоятельно.
Самостоятельно: проиллюстрировать теорему
на двух примерах.
28.
2. Сходящаяся последовательность имееттолько один предел.
Доказательство самостоятельно.
3. Сходящаяся последовательность
ограниченна.
Самостоятельно: проиллюстрировать теорему
на двух примерах.
Замечание 3. Обратное не верно.
Пример.
xn ( 1)
n 1
.
29.
4. Алгебраические свойства сходящихсяпоследовательностей.
lim xn a
n
а)
б)
lim yn b
n
lim ( xn yn ) a b
n
lim ( xn y n ) a b
n
30.
в)г)
lim ( xn yn ) a b
n
xn a
lim
n y n
b
b 0
Доказать самостоятельно свойство а).
Самостоятельно: проиллюстрировать каждый
пункт на двух примерах.
31.
п.5. Предельный переход в неравенствах.Теорема 2. Если lim xn a, и, начиная с
n
некоторого номера xn b, то a b.
32.
Следствие.lim xn a
n
lim yn b
n
xn y n
a b
33.
Теорема 3 (Вейерштрасс).Монотонная ограниченная
последовательность сходится.
Пример.
1
xn 1
n
xn ─ возрастающая
2 xn 3
n
n
1
lim 1 e
n
n
e 2,71828 ...



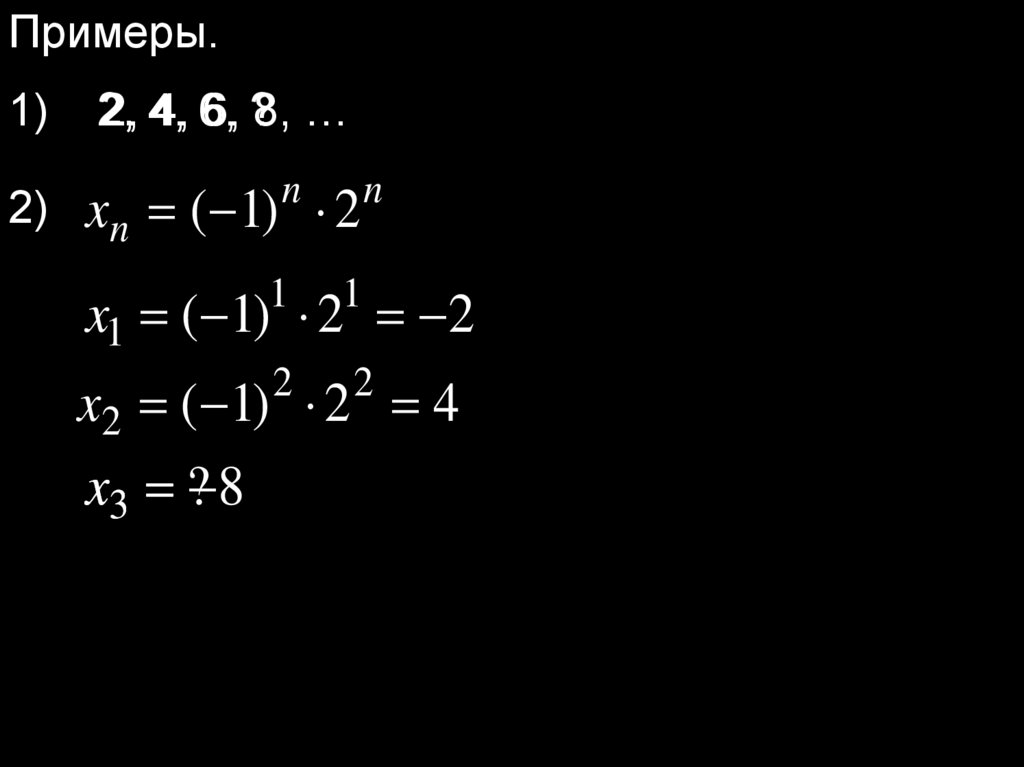


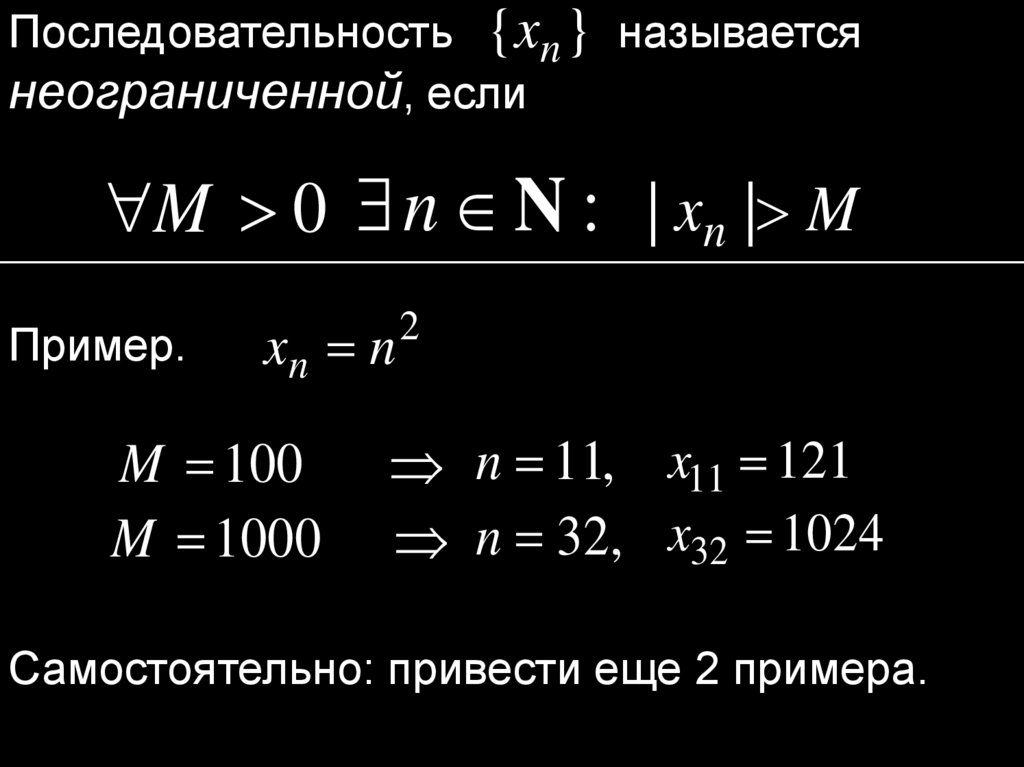







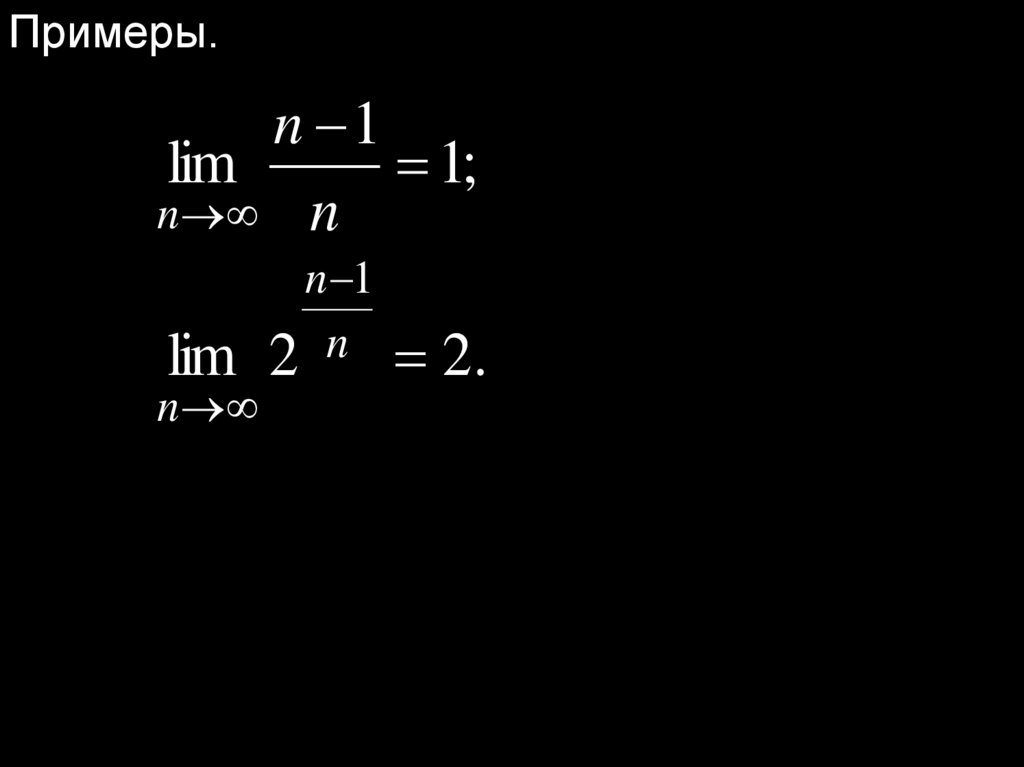


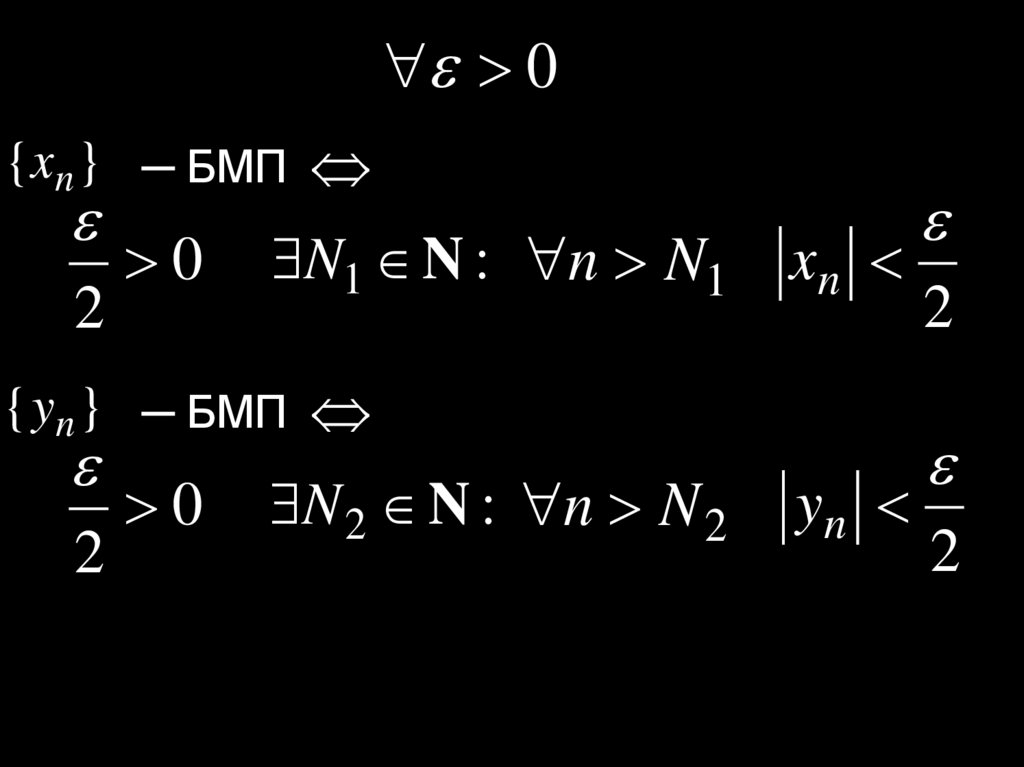
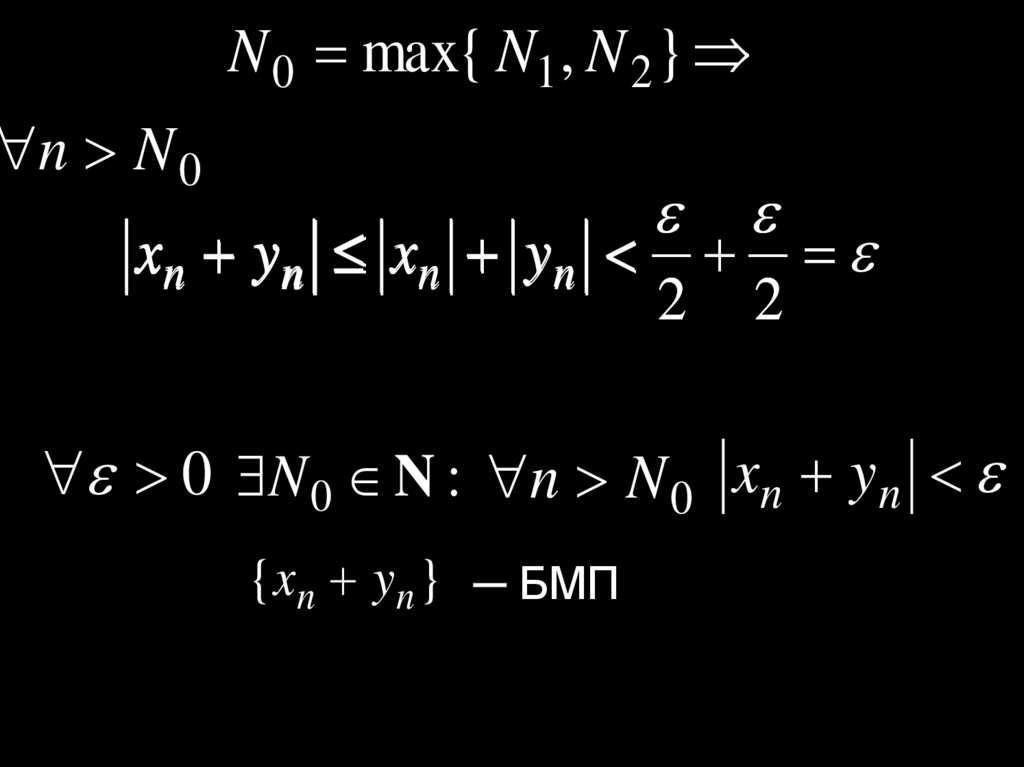













 mathematics
mathematics








