Similar presentations:
Предел числовой последовательности
1.
§15. Предел числовойпоследовательности
п.1. Кванторы.
─ квантор существования («существует»)
─ квантор общности («для любого»)
2.
Окрестностью точки называется любойинтервал, содержащий эту точку.
x
- окрестностью точки a называется
интервал (a ; a ).
a
a
a
x
3.
п.2. Основные понятия.Числовой последовательностью
называется правило, согласно которому
каждому натуральному числу n поставлено в
соответствие действительное число xn.
Обозначение:
{xn }, xn , n N.
4.
Примеры.1)
2, 4, 6, ?8, …
2)
xn ( 1) 2
n
n
x1 ( 1) 2 2
1
1
x2 ( 1) 2 4
x3 ? 8
2
2
5.
Последовательностьограниченной, если
{xn }
называется
M 0 n N : | xn | M
Геометрическая интерпретация
M xn
x3
x1 x2
M
x
6.
Пример.2
xn 1
n
1
1
2
x4
M 1
1
3
0
x3 x2
x1 1?
x2 ?0
1
x3 ?
3
1
x4 ?
2
1
x1
Самостоятельно: привести еще 2 примера.
x
7.
Последовательность {xn } называетсянеограниченной, если
M 0 n N : | xn | M
Пример.
xn n
M 100
M 1000
2
n 11, x11 121
n 32, x32 1024
Самостоятельно: привести еще 2 примера.
8.
Последовательностьпостоянной, если
{xn }
называется
n N : xn a, a const .
Пример.
xn 2
x1 2,
x2 2,...
9.
Последовательность {xn } называетсявозрастающей, если
n N :
n
Пример. xn
,
2
xn xn 1.
[x ] ─ целая часть x.
0,
0,1,1,2,2,3,3,…
0,1,1,?
0,1,?
Самостоятельно: привести еще 2 примера.
10.
Последовательностьубывающей, если
n N :
{xn }
называется
xn xn 1.
100
Пример. xn
.
n
Самостоятельно: привести еще 2 примера.
Возрастающие
Убывающие
Монотонные последовательности
11.
Последовательностьназывается
строго возрастающей, если
n N :
Пример.
{xn }
xn xn 1.
xn n .
2
Последовательность
{xn }
называется
строго убывающей, если
n N :
xn xn 1.
Пример. xn n.
Самостоятельно: привести еще по 2 примера.
12.
Строго возрастающиеСтрого убывающие
Строго монотонные последовательности
Самостоятельно: привести 2 примера
последовательностей, не являющихся
монотонными.
13.
п.3. Предел числовой последовательности.n 1
Пример. xn
.
n
x1
x2
0
1
2
x3 x4
2 3
3 4
1
x
1
1
1
x1 1 1, x2 1 , x3 1 , x4 1 ,...
4
2
3
xn 1 ?0
xn 1?
14.
Число a называется пределомпоследовательности {xn }, если
для любого действительного числа
можно указать такое натуральное число N0,
что для всех элементов последовательности с
номерами большими, чем N0, будет
выполняться неравенство
xn a .
lim xn a 0 N0 N : n N 0
n
xn a
15.
Примеры.n 1
lim
1;
n n
lim
n
n 1
2 n
2.
16.
Геометрический смысл пределапоследовательности
x1
x2
xN0 2
a
Пример. xn
x1
1
x3
1
9
a
( 1)
n
xN0 1 x N 0 x3
n
2
x
1
a 0
200
x14 x2
x16
.
x15
1 1
200 225
a
0
1
1
256
1
200 196
1 x
4
17.
Последовательностьназывается
бесконечно малой (БМП), если
{xn }
0 N0 N : n N 0
lim xn 0
xn
n
1
Пример. xn .
n
Самостоятельно: привести еще 2 примера.
18.
Свойства БМП1. Сумма двух БМП есть БМП.
Доказательство.
{xn } ─ БМП
{ yn } ─ БМП
{xn yn } ─ БМП ?
19.
0{xn } ─ БМП
2
0
N1 N : n N1
xn
{ yn } ─ БМП
2
0
N 2 N : n N 2
yn
2
2
20.
N0 max{ N1, N 2}n N 0
xn yn xn yn
2
2
0 N0 N : n N 0 xn yn
{xn yn } ─ БМП
21.
2. БМП ─ ограниченная последовательность.3. Произведение двух БМП есть БМП.
4. Произведение БМП и ограниченной
последовательности есть БМП.
5. Если
{xn } ─ постоянная и БМП, то
n N xn 0.
22.
Последовательностьназывается
бесконечно большой (ББП), если
{xn }
A 0 N0 N : n N 0
xn A
lim xn lim xn , lim xn
n
n
n
Примеры. xn ln n;
xn n.
Самостоятельно: привести еще 2 примера.
23.
Свойства ББП1.ББП ─ неограниченная последовательность.
2. Произведение двух ББП есть ББП.
3. Сумма ББП и ограниченной
последовательности есть ББП.
4. ББП не может являться постоянной
последовательностью.
24.
Замечание 1. Сумма двух ББП не обязательноявляется ББП.
Пример.
xn n,
yn n.
xn yn 0.
25.
Связь между БМП и ББПТеорема 1. Если {xn } ─ ББП и
n N xn 0,
1
то ─ БМП.
xn
Обратно, если {xn } ─ БМП и n N xn 0,
1
то ─ ББП.
xn
Самостоятельно: проиллюстрировать теорему
на двух примерах.
26.
Замечание 2.1) Если
{xn }
lim xn a, то говорят, что
n
сходится к числу
2) Если
a; {xn } ─ сходящаяся.
lim xn , то говорят, что
n
{xn } сходится к
.
3) Если{xn }не имеет предела, то говорят, что
{xn } расходится.
Пример. xn ( 1) : 1, 1, 1, 1, ....
n
27.
п.4. Свойства сходящихсяпоследовательностей.
1. Для того, чтобы последовательность {xn }
имела своим пределом число a, необходимо и
достаточно, чтобы последовательность {xбыла
n a}
БМП.
lim xn a {xn a}
n
─ БМП
Доказательство самостоятельно.
Самостоятельно: проиллюстрировать теорему
на двух примерах.
28.
2. Сходящаяся последовательность имееттолько один предел.
Доказательство самостоятельно.
3. Сходящаяся последовательность
ограниченна.
Самостоятельно: проиллюстрировать теорему
на двух примерах.
Замечание 3. Обратное не верно.
Пример.
xn ( 1)
n 1
.
29.
4. Алгебраические свойства сходящихсяпоследовательностей.
lim xn a
n
а)
б)
lim yn b
n
lim ( xn yn ) a b
n
lim ( xn yn ) a b
n
30.
в)г)
lim ( xn yn ) a b
n
xn a
lim
n yn
b
b 0
Доказать самостоятельно свойство а).
Самостоятельно: проиллюстрировать каждый
пункт на двух примерах.
31.
п.5. Предельный переход в неравенствах.Теорема 2. Если lim xn a, и, начиная с
n
некоторого номера xn b, то a b.
32.
Следствие.lim xn a
n
lim yn b
n
xn yn
a b
33.
Теорема 3 (Вейерштрасс).Монотонная ограниченная
последовательность сходится.
Пример.
xn
1
xn 1
n
─ возрастающая
2 xn 3
n
n
1
lim 1 e
n
n
e 2,71828...



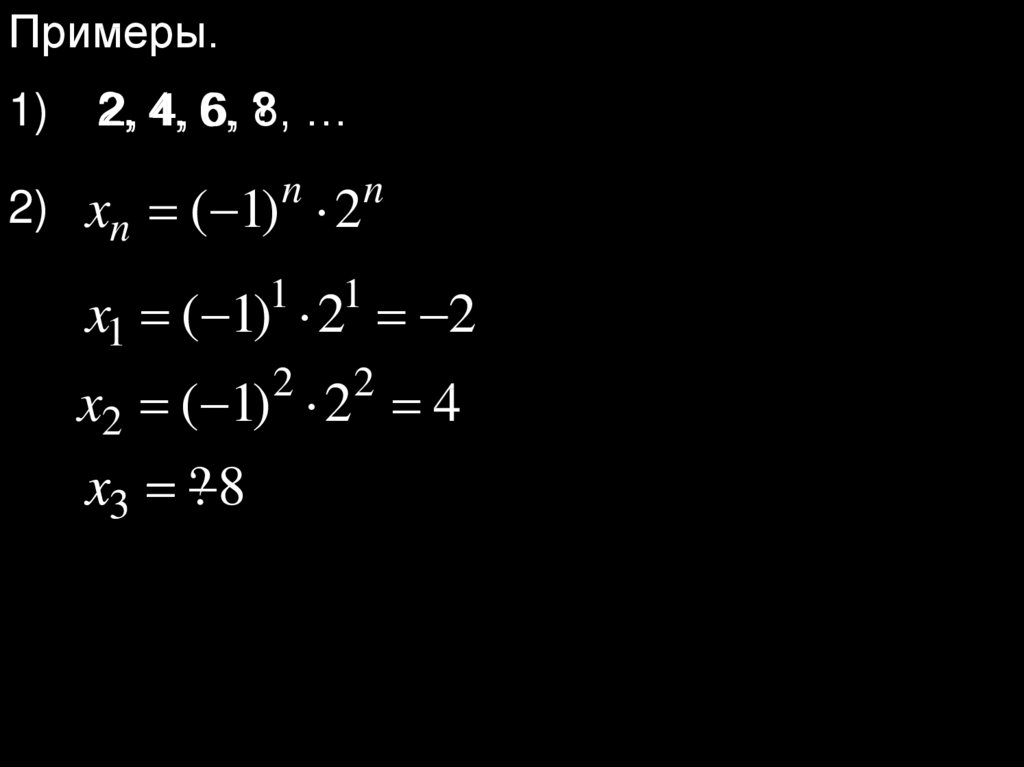


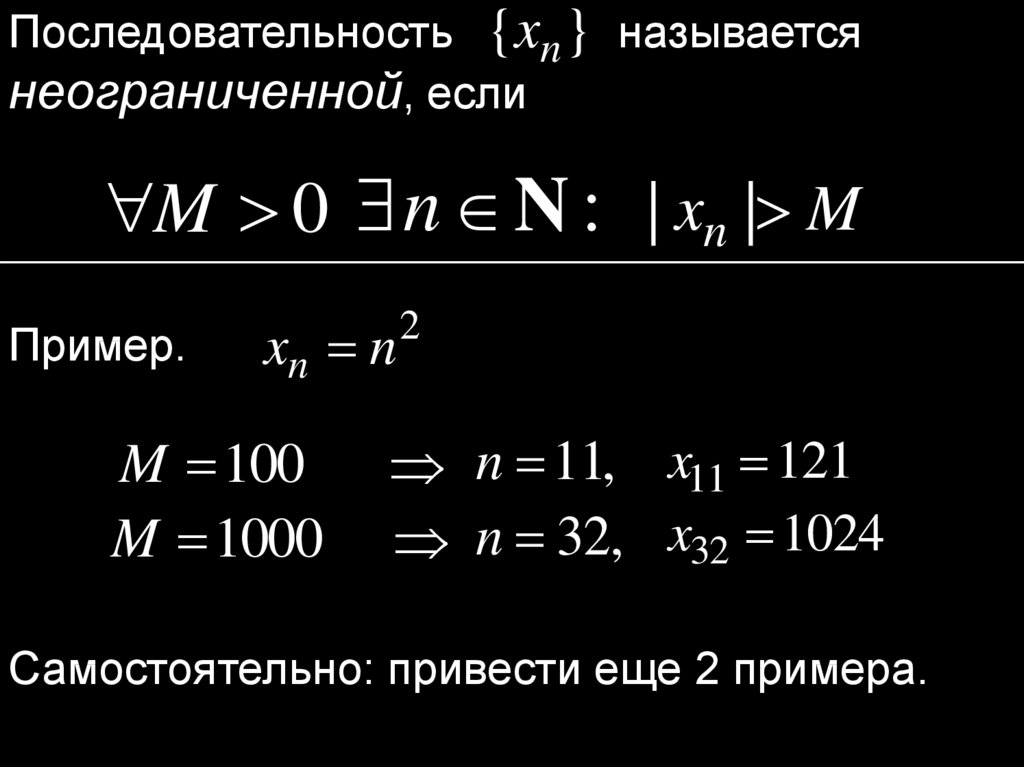











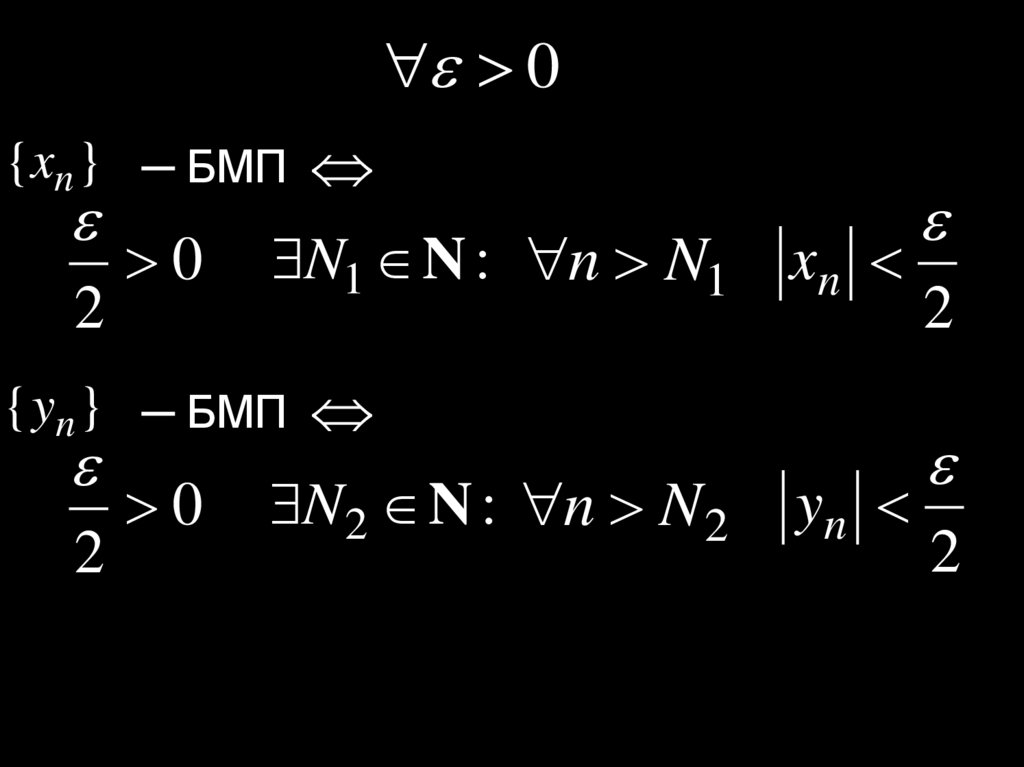
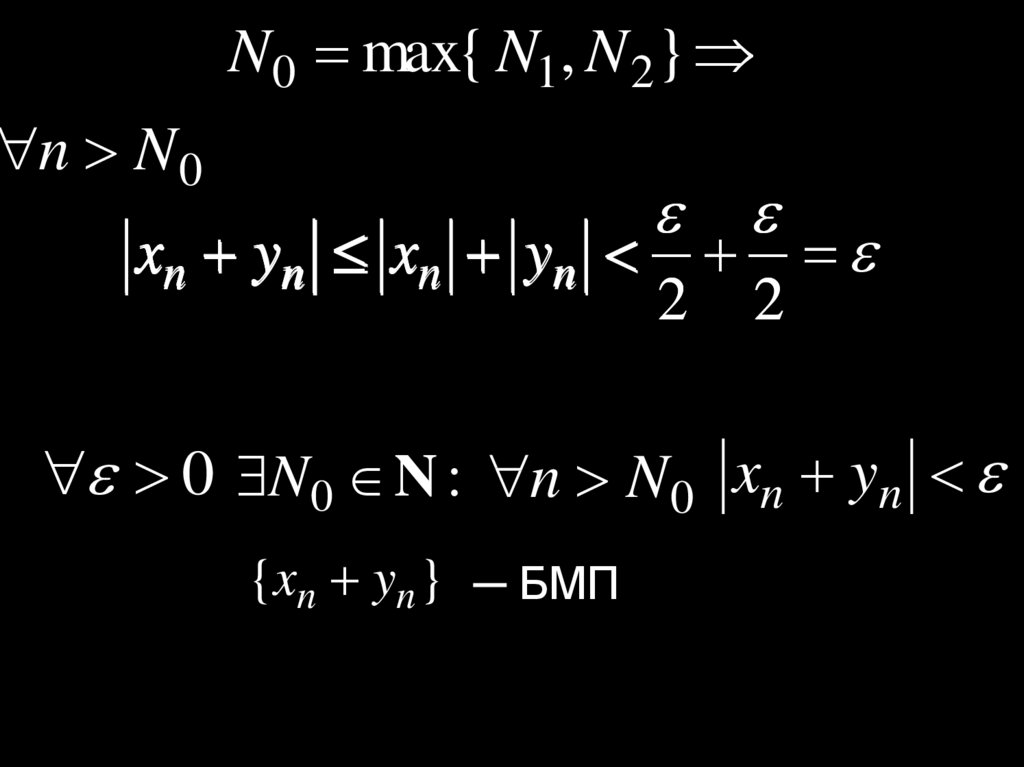













 mathematics
mathematics








