Угол между прямой и плоскостью. Угол между плоскостями

1.

Угол между прямой и плоскостью.
Угол между плоскостями

2.

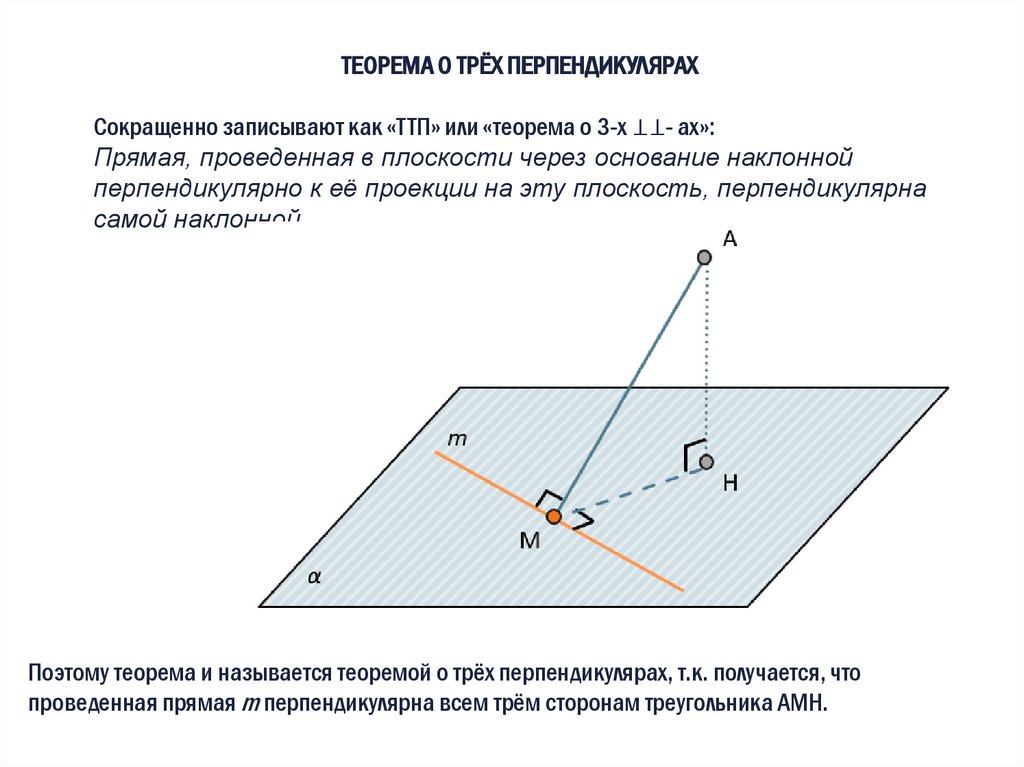
ТЕОРЕМА О ТРЁХ ПЕРПЕНДИКУЛЯРАХ
Сокращенно записывают как «ТТП» или «теорема о 3-х ⊥⊥- ах»:
Прямая, проведенная в плоскости через основание наклонной
перпендикулярно к её проекции на эту плоскость, перпендикулярна
самой наклонной.
Поэтому теорема и называется теоремой о трёх перпендикулярах, т.к. получается, что
проведенная прямая m перпендикулярна всем трём сторонам треугольника АМН.

3.

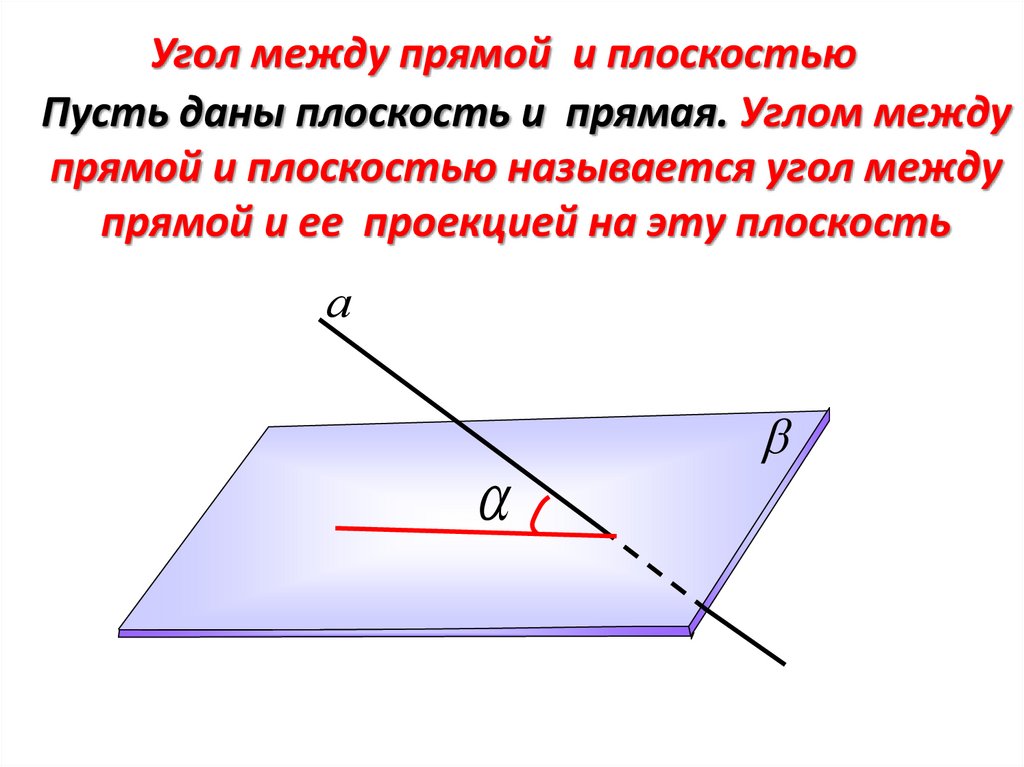
Угол между прямой и плоскостью
Пусть даны плоскость и прямая. Углом между
прямой и плоскостью называется угол между
прямой и ее проекцией на эту плоскость
а

4.

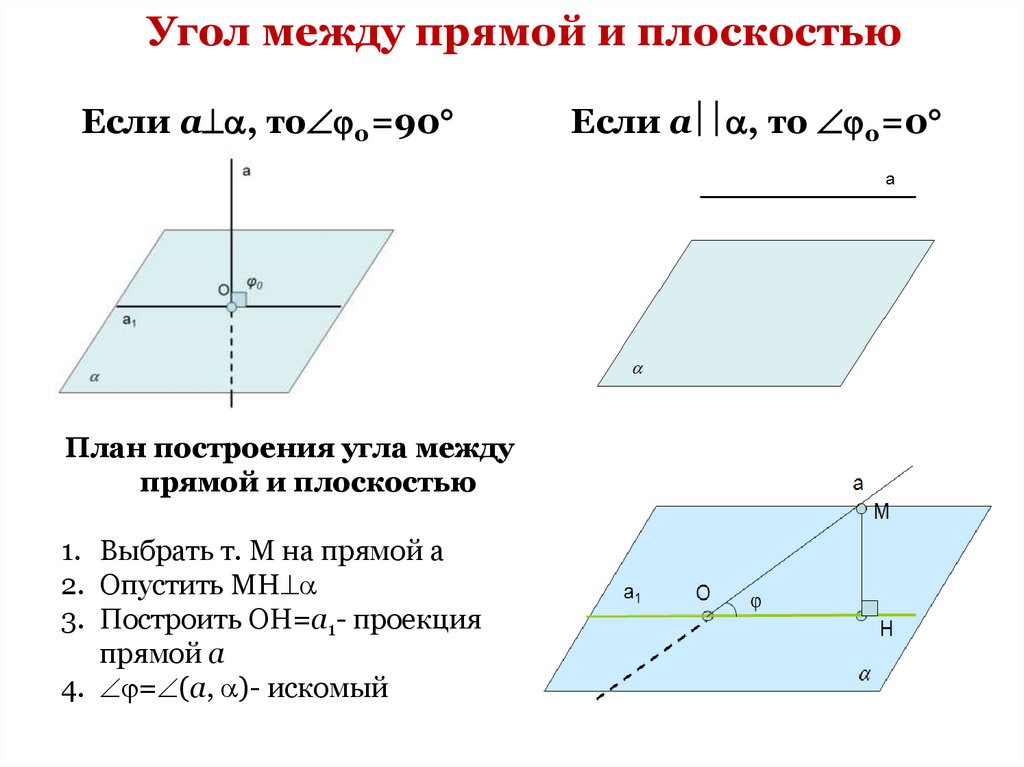
Если прямая параллельна плоскости, то угол
между ней и плоскостью считается равным
нулю.
Если прямая перпендикулярна плоскости, то
угол между ней и плоскостью прямой, т. е.
равен 90°.
а
а
0
90

5.

Угол между прямой и плоскостью
Если а , то 0=90
План построения угла между
прямой и плоскостью
1. Выбрать т. М на прямой а
2. Опустить МН
3. Построить ОН=а1- проекция
прямой а
4. = (а, )- искомый
Если а , то 0=0