Similar presentations:
Методы решения рациональных алгебраических уравнений
1.
Владетьматематическими
методами анализа
данных должны все –
инженеры, экономисты,
юристы, строители,
государственные
деятели.
Н.А.Назарбаев
2.
Как показывает мироваяпрактика, высокий уровень
математической подготовки
обеспечит качественный
рывок во всех отраслях.
Н.А.Назарбаев
3.
Тема урока:«Методы решения
рациональных
алгебраических
уравнений»
4. Уравнения со степенью больше 2
Для решения таких уравнений чаще всего применяютследующие методы:
разложение на множители;
введение новой переменной.
Метод разложения на множители
Путем группировки слагаемых и применяя
формулу сокращенного умножения, приводим
исходное уравнение к виду, когда слева записано
произведение нескольких множителей, а справа – нуль.
Затем приравниваем каждый из множителей.
7. Задание: Решите уравнение х³ - 3х + 2 = 0
5.
Решение: х³ - 3х + 2 = 0х³ - х – 2х + 2 = 0
х(х²- 1) – 2(х-1) = 0
х (х-1)(х+1) – 2(х-1) = 0
(х - 1)(х²+х – 2) = 0
1) х – 1 = 0
2) х² + х – 2 = 0
х= 1
х= -2 х= 1
Ответ: - 2; 1
6.
Методы введения новой переменнойИщем в уравнении некоторое повторяющееся выражение,
которое обозначаем за новую переменную, упрощая тем
самым вид уравнения.
11. Задание: (х² + х – 2)(х² + х – 3) = 12.
Решение:
Обозначим х² + х – 3 = а, тогда (а + 1)а = 12
а² + а – 12 = 0
а= -4, а= 3
1) х ² + х - 3 = - 4
2) х ² + х – 3 = 3
х²+х+1=0
х²+х–6=0
уравнение решений не имеет,
х= - 3, х= 2
Так как D < 0
Ответ: - 3; 2
7.
В более сложных случаях замена видна лишь после некоторыхпреобразований.
12. Задание: Решите уравнение
(х² + 2х)² - (х + 1)² = 55.
Решение: Переписав уравнение иначе, а именно:
(х² + 2х)² - (х² + 2х + 1) = 55
Мы сразу видим замену : х ² + 2х = а.
а² - а - 56 = 0
а= -7, а= 8
1) а = - 7
2) а = 8
х ² + 2х + 7 = 0
х ² + 2х - 8= 0
уравнение решений не имеет,
х= 2, х= -4
так как D < 0
Ответ: - 4; 2
8.
16. Задание: Решите уравнение(х - 4)(х - 5)(х - 6)(х - 7) = 1680.
Решение:
(х - 4)(х - 7)(х - 5)(х - 6) = 1680
(х² - 11х + 28)(х ² - 11х + 30) = 1680
Обозначим: х ² - 11х + 28 = а, тогда
а(а + 2) = 1680
а²+ 2а – 1680 = 0
а= - 42, а= 40
1) х² - 11х + 28 = - 42
2) х² - 11х + 28 = 40
х² - 11х + 70 = 0
х² - 11х - 12 = 0
уравнение решений не имеет,
х= 12, х= -1
так как D < 0
Ответ: -1; 12
9. Нестандартный подход
Общих формул нахождения корнейалгебраических уравнений высоких степеней нет,
и поэтому об их решениях говорят как об
искусстве решать пример нестандартно,
придумать «свой метод», догадаться что-то
прибавить и отнять, выделить полный квадрат,
на что-то разделить и умножить и т.д.
10. Домашнее задание:
11. Решение дробно – рациональных уравнений
При решении дробно – рациональных уравненийследует учесть, что областью определения уравнения
являются те значения переменной х, при которых
знаменатели дробей не обращаются в нуль.
При решении дробно – рациональных уравнений
целесообразно поступать следующим образом:
1) найти общий знаменатель дробей, входящих в
уравнение, если каждая дробь имеет смысл;
2) заменить данное уравнение целым, умножив обе
его части на общий знаменатель;
3) решить получившееся целое уравнение;
4) исключить из его корней те, которые обращают
в нуль общий знаменатель.




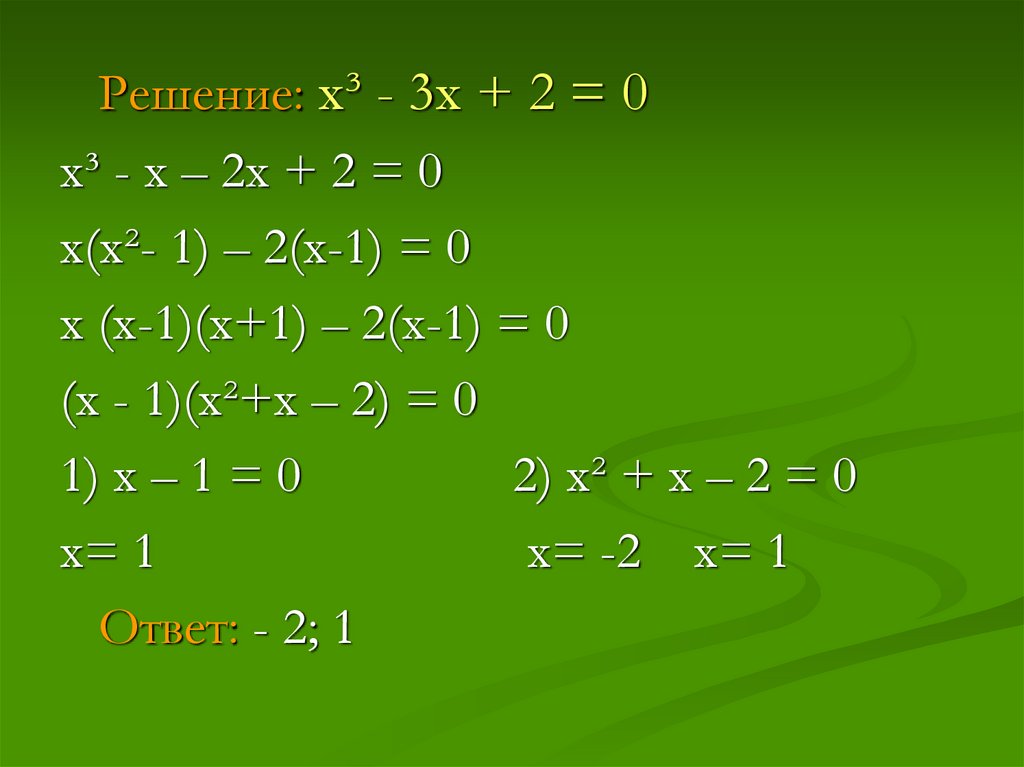







 mathematics
mathematics








