Similar presentations:
Теоретическая механика
1. Теоретическая механика
2. 8. Кинематика. Основные понятия кинематики.
3.
8.1.Основные кинематические параметрыа) Траектория
Линию, которую очерчивает материальная точка при
движении в пространстве, называют траекторией.
Траектория может быть прямой и кривой, плоской и
пространственной линией.
Уравнение траектории при плоском движении: у = f(x).
б) Пройденный путь
Путь измеряется вдоль траектории в направлении
движения. Обозначение — s, единицы измерения —
метры.
4.
в) Уравнение движения точкиУравнение, определяющее положение движущейся точки в
зависимости от времени, называется уравнением движения.
Положение точки в каждый момент времени можно определить по
расстоянию, пройденному вдоль траектории от некоторой
неподвижной точки,
рассматриваемой как начало отсчета (рис. 9.1).
Такой способ задания движения называется естественным.
5.
Таким образом, уравнение движения можно представить в видеS = f (t).
Положение точки можно также определить, если известны ее
координаты в зависимости от времени
(рис. 9.2). Тогда в случае движения на плоскости должны быть
заданы два уравнения:
В случае пространственного движения добавляется и третья
координата
z = f3(t)
Такой способ задания движения называют координатным.
6.
г) Скорость движенияВекторная величина, характеризующая в данный момент быстроту
и направление движения по траектории, называется
скоростью.
Скорость — вектор, в любой момент направленный по
касательной к траектории в сторону направления движения
(рис. 9.3).
Если точка за равные промежутки времени проходит равные
расстояния, то движение называют равномерным.
Рис.9.3. Скорость движения.
7.
Средняя скорость на пути AS определяется какгде ΔS — пройденный путь за время Δt;
Δt — промежуток времени.
Если точка за равные промежутки времени проходит неравные
"пути, то движение называют неравномерным.
В этом случае скорость — величина переменная и зависит от
времени v = f(t).
При рассмотрении малых промежутков времени (Δt → 0) средняя
скорость становится равной истинной скорости движения в
данный момент. Поэтому скорость в данный момент
определяют как производную по времени:
За единицу скорости принимают 1м/с. Иногда скорость измеряют в
км/ч,
8.
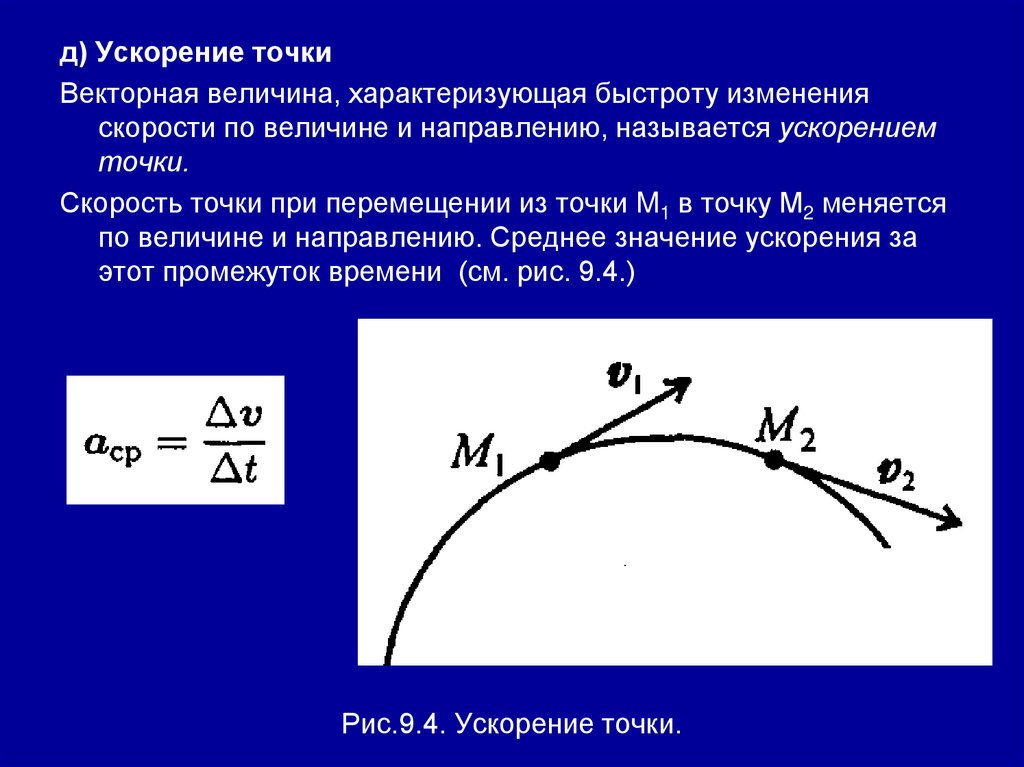
д) Ускорение точкиВекторная величина, характеризующая быстроту изменения
скорости по величине и направлению, называется ускорением
точки.
Скорость точки при перемещении из точки M1 в точку М2 меняется
по величине и направлению. Среднее значение ускорения за
этот промежуток времени (см. рис. 9.4.)
Рис.9.4. Ускорение точки.
9.
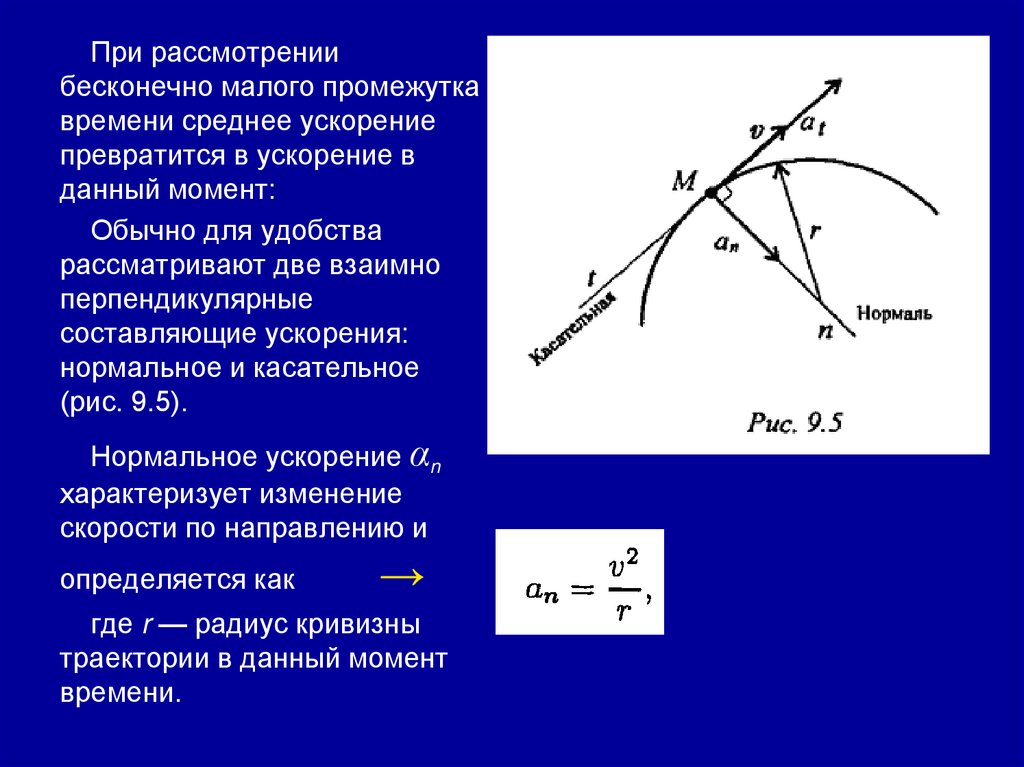
При рассмотрениибесконечно малого промежутка
времени среднее ускорение
превратится в ускорение в
данный момент:
Обычно для удобства
рассматривают две взаимно
перпендикулярные
составляющие ускорения:
нормальное и касательное
(рис. 9.5).
Нормальное ускорение αn
характеризует изменение
скорости по направлению и
определяется как
→
где r — радиус кривизны
траектории в данный момент
времени.
10.
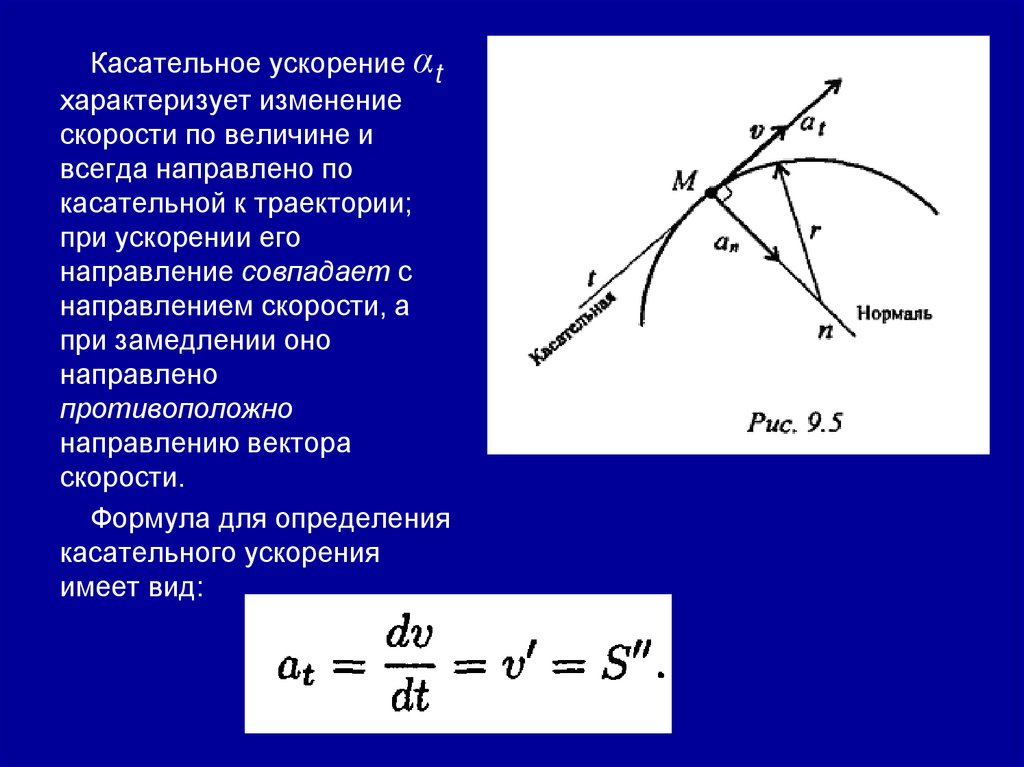
Касательное ускорение αtхарактеризует изменение
скорости по величине и
всегда направлено по
касательной к траектории;
при ускорении его
направление совпадает с
направлением скорости, а
при замедлении оно
направлено
противоположно
направлению вектора
скорости.
Формула для определения
касательного ускорения
имеет вид:
11.
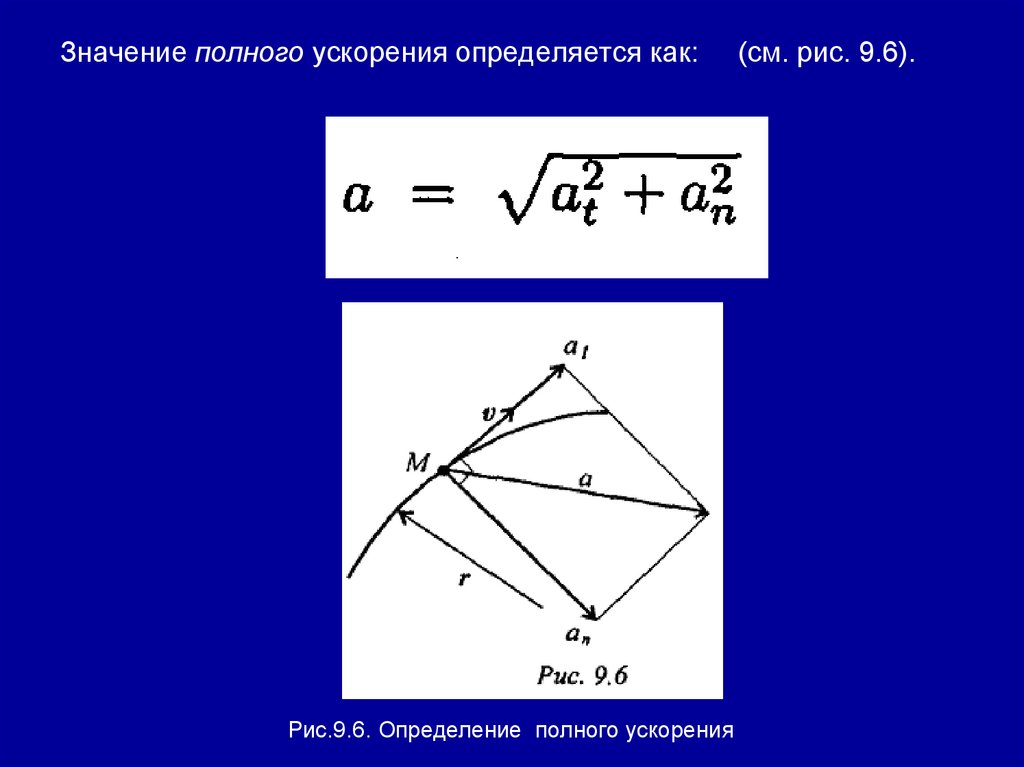
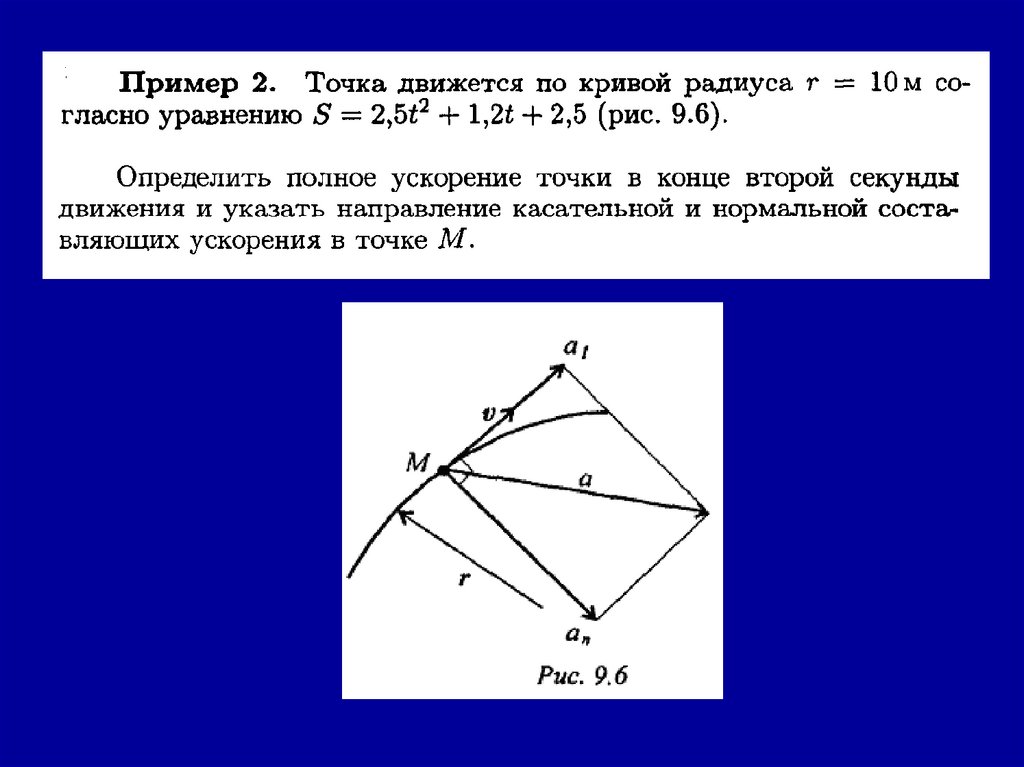
Значение полного ускорения определяется как:Рис.9.6. Определение полного ускорения
(см. рис. 9.6).
12.
13.
14.
15. 9.Кинематика точки.
16.
9.1. Анализ видов и кинетических параметров движенийа) Равномерное движение
Равномерное движение — это движение с постоянной скоростью:
v = const.
Для прямолинейного равномерного движения (рис. 10.1а)
Рис.10.1.
Полное ускорение движения точки равно нулю: а = 0.
17.
При криволинейном равномерном движении (рис. 10.1б)рис. 10.1б
Полное ускорение равно нормальному ускорению:
α = αn
Уравнение (закон) движения точки при равномерном движении
можно получить, проделав ряд несложных операций.
Так как v = const, закон равномерного движения в общем виде
является уравнением прямой:
S = So+vt,
где So — путь, пройденный до начала отсчета.
18.
б)Равнопеременное движениеРавнопеременное движение — это движение с постоянным
касательным ускорением:
at = const.
Для прямолинейного равнопеременного движения
Полное ускорение равно касательному ускорению.
Криволинейное равнопеременное движение (рис. 10.2):
рис. 10.2
19.
значение скорости при равнопеременном движениизакон равнопеременного движения в общем виде,
20.
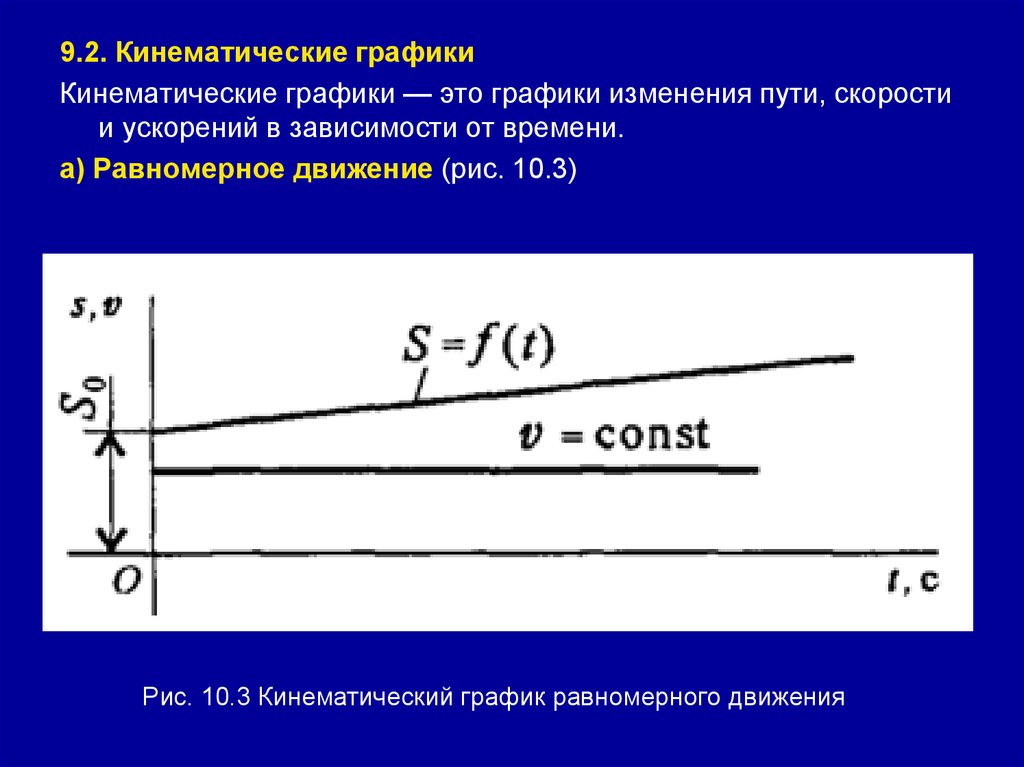
9.2. Кинематические графикиКинематические графики — это графики изменения пути, скорости
и ускорений в зависимости от времени.
а) Равномерное движение (рис. 10.3)
Рис. 10.3 Кинематический график равномерного движения
21.
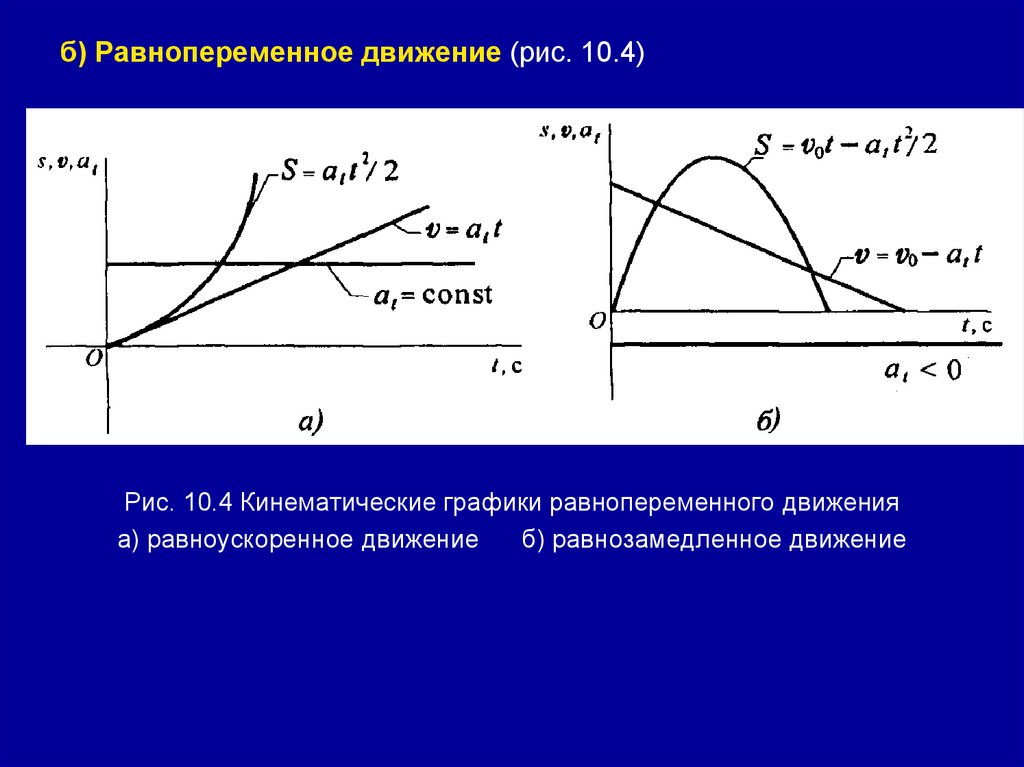
б) Равнопеременное движение (рис. 10.4)Рис. 10.4 Кинематические графики равнопеременного движения
а) равноускоренное движение
б) равнозамедленное движение
22.
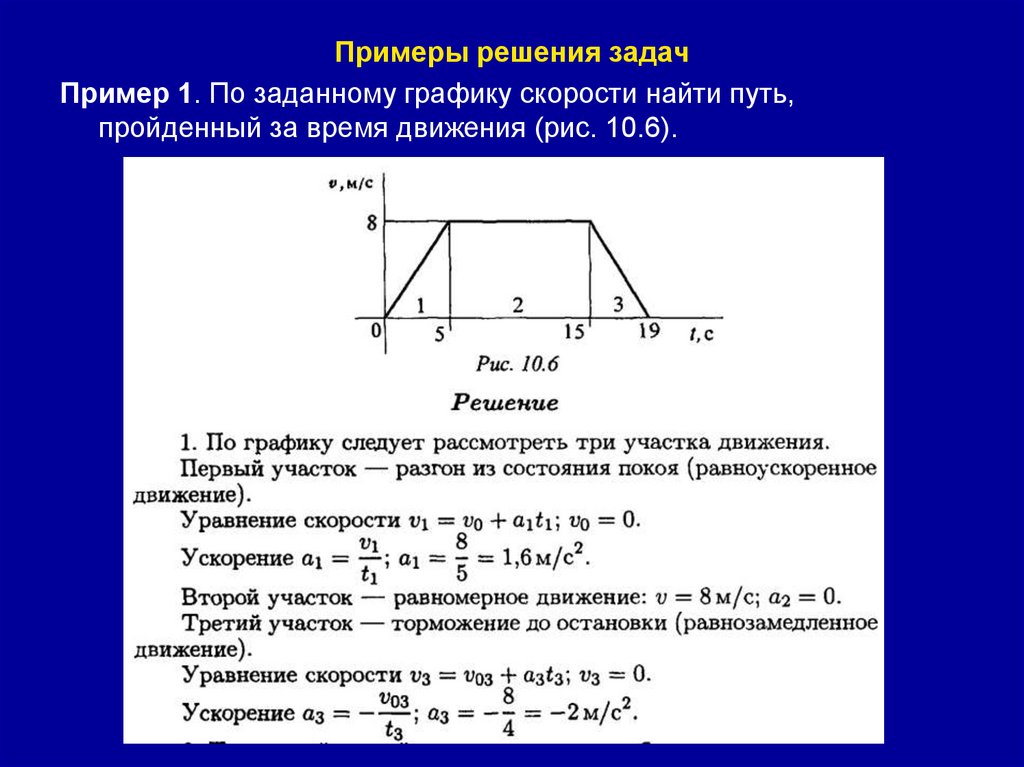
Примеры решения задачПример 1. По заданному графику скорости найти путь,
пройденный за время движения (рис. 10.6).
23.
24.
Пример 2. Тело, имевшее начальную скорость 36 км/ч, прошло50 м до остановки. Считая движение равнозамедленным,
определить время торможения.
25. 10.Простейшие движения твердого тела.
26.
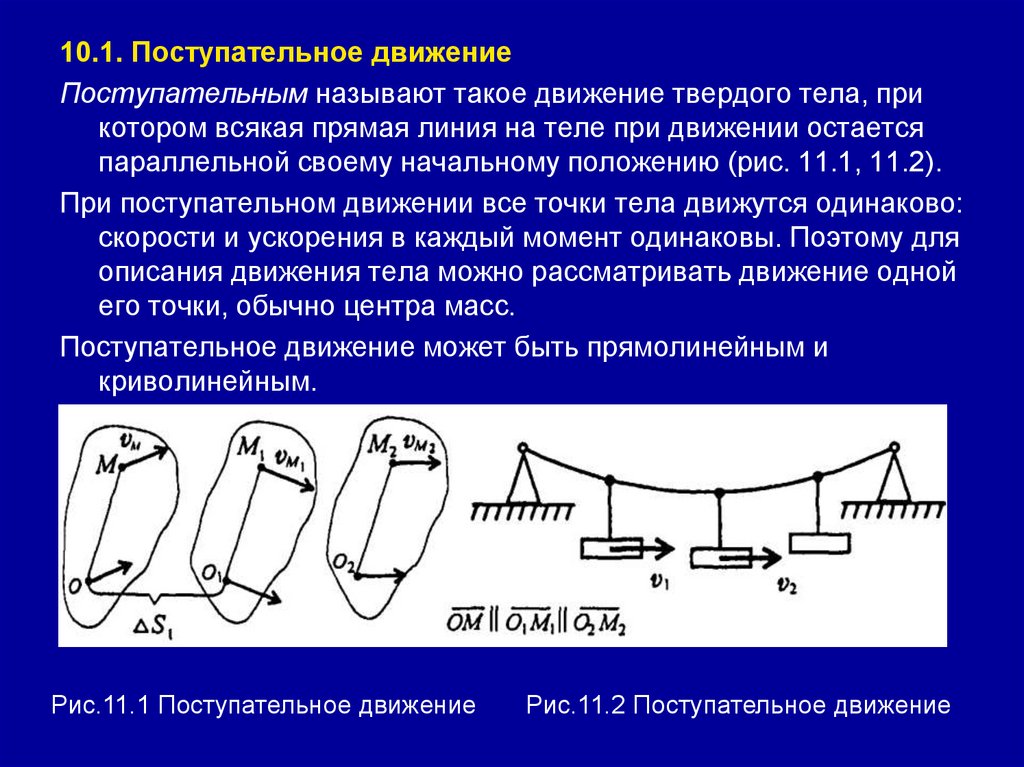
10.1. Поступательное движениеПоступательным называют такое движение твердого тела, при
котором всякая прямая линия на теле при движении остается
параллельной своему начальному положению (рис. 11.1, 11.2).
При поступательном движении все точки тела движутся одинаково:
скорости и ускорения в каждый момент одинаковы. Поэтому для
описания движения тела можно рассматривать движение одной
его точки, обычно центра масс.
Поступательное движение может быть прямолинейным и
криволинейным.
Рис.11.1 Поступательное движение
Рис.11.2 Поступательное движение
27.
10.2. Вращательное движениеПри вращательном движении
все точки тела описывают окружности вокруг общей неподвижной
оси.
Неподвижная ось, вокруг которой
вращаются все точки тела
называется осью вращения.
При этом каждая точка движется
по окружности, радиус которой
равен расстоянию точки до оси
вращения. Точки на оси вращения
не перемещаются.
Рис.11.3. Вращательное движение
Для описания вращательного
движения тела вокруг неподвижной
оси можно использовать только
φ — угол поворота тела, [φ]= рад;
угловые параметры (рис. 11.3):
ω — угловая скорость, определяет
изменение угла поворота в единицу
времени, [ω] = рад/с.
28.
Для определения положения тела в любой момент временииспользуется уравнение
φ = f(t).
Следовательно, для определения угловой скорости можно
пользоваться выражением:
Иногда для оценки быстроты вращения используют угловую
частоту вращения n, которая оценивается в оборотах в минуту.
Угловая скорость и частота вращения физически близкие
величины:
Изменение угловой скорости во времени определяется угловым
ускорением ε, [ε] = рад/с2;
29.
11.3. Частные случаи вращательного движенияа) Равномерное вращение (угловая скорость постоянна):
ω - const.
Уравнение (закон) равномерного вращения в данном случае имеет
вид:
где φ0 — угол поворота до начала отсчета.
Кинематические графики для этого вида движения изображены на
рис. 11.4.
Рис.11.4. Кинематические графики равномерного вращения
30.
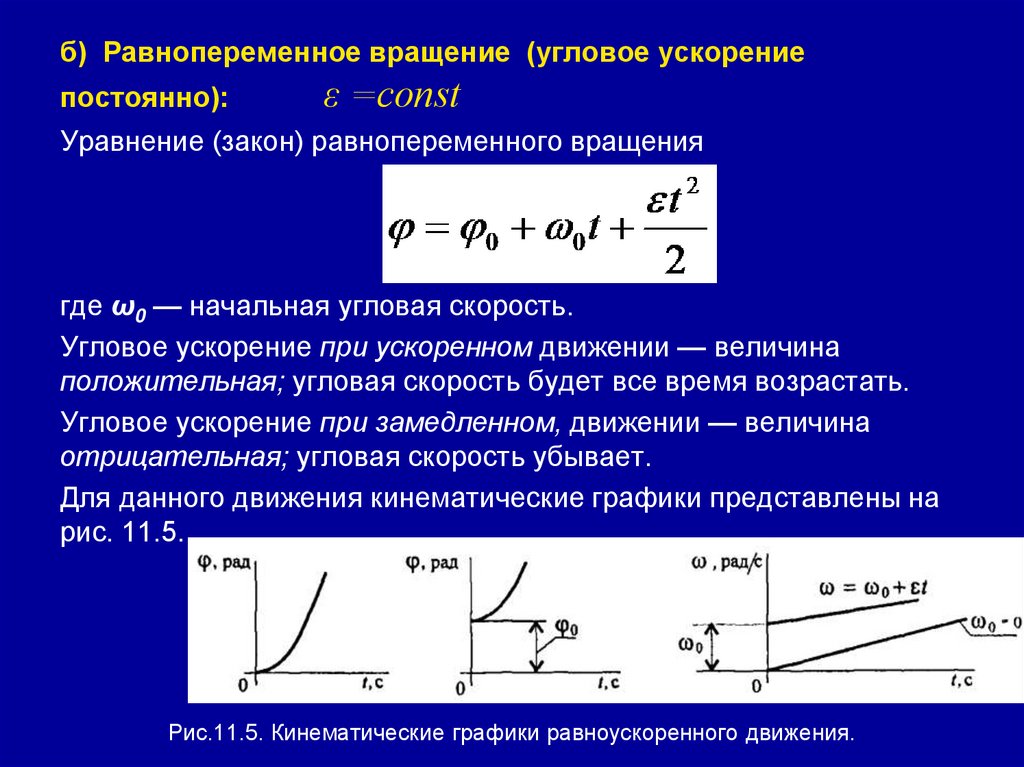
б) Равнопеременное вращение (угловое ускорениепостоянно):
ε =const
Уравнение (закон) равнопеременного вращения
где ω0 — начальная угловая скорость.
Угловое ускорение при ускоренном движении — величина
положительная; угловая скорость будет все время возрастать.
Угловое ускорение при замедленном, движении — величина
отрицательная; угловая скорость убывает.
Для данного движения кинематические графики представлены на
рис. 11.5.
Рис.11.5. Кинематические графики равноускоренного движения.
31.
в) Скорости и ускорения точек вращающегося тела.Тело вращается вокруг точки О. Определим параметры движения
точки А, расположенной на расстоянии rA от оси вращения (рис.
11.6, 11.7).
Путь точки A:
SA = ωrA
Линейная скорость точки A: vA = ωrA
Ускорения точки A: at A = εrA — касательное;
an A = ω2rA — нормальное,
где rA — радиус окружности, траектории точки А.
32.
Преобразование форм движенияВ движущихся элементах машин часто происходят
преобразования движений:
-преобразование одного вращательного движения в
другое;
-преобразование вращательного движения
в поступательное и наоборот.
33.
Преобразования эти происходят с помощью-зубчатых или фрикционных передач (а, в);
-ременных или цепных передач (б).
а),б)
в)
34.
Связи между скоростями двух различных движенийназываются кинематическими связями.
Кинематические связи устанавливаются из условия
отсутствия проскальзывания между взаимодействующими телами.
35.
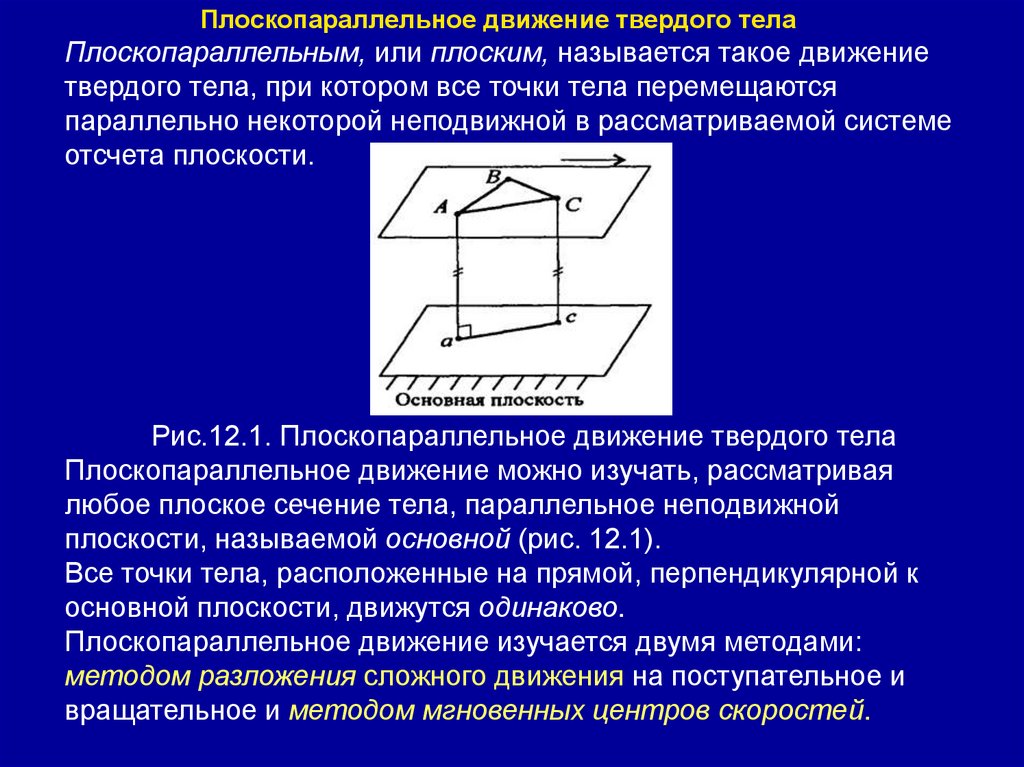
Плоскопараллельное движение твердого телаПлоскопараллельным, или плоским, называется такое движение
твердого тела, при котором все точки тела перемещаются
параллельно некоторой неподвижной в рассматриваемой системе
отсчета плоскости.
Рис.12.1. Плоскопараллельное движение твердого тела
Плоскопараллельное движение можно изучать, рассматривая
любое плоское сечение тела, параллельное неподвижной
плоскости, называемой основной (рис. 12.1).
Все точки тела, расположенные на прямой, перпендикулярной к
основной плоскости, движутся одинаково.
Плоскопараллельное движение изучается двумя методами:
методом разложения сложного движения на поступательное и
вращательное и методом мгновенных центров скоростей.
36.
т.С - полюсХс , ус - координаты полюса
Vс- скорость точки полюса
ас-ускорение точки полюса
- Уравнения плоскопараллельного движения
37.
38.
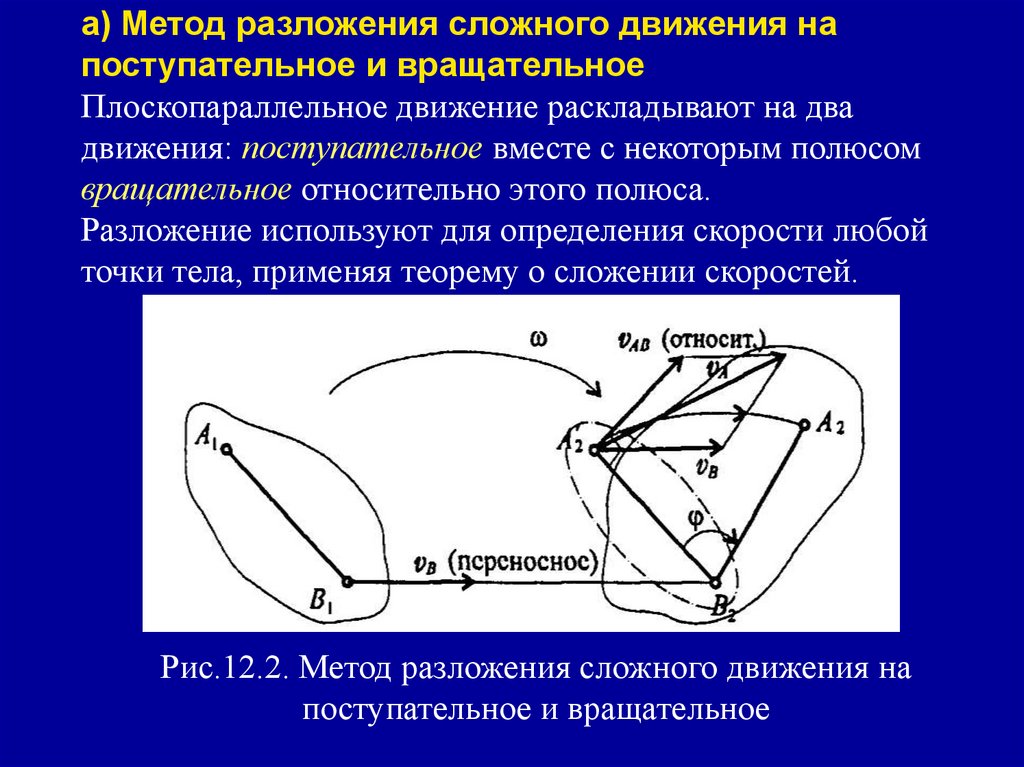
а) Метод разложения сложного движения напоступательное и вращательное
Плоскопараллельное движение раскладывают на два
движения: поступательное вместе с некоторым полюсом
вращательное относительно этого полюса.
Разложение используют для определения скорости любой
точки тела, применяя теорему о сложении скоростей.
Рис.12.2. Метод разложения сложного движения на
поступательное и вращательное
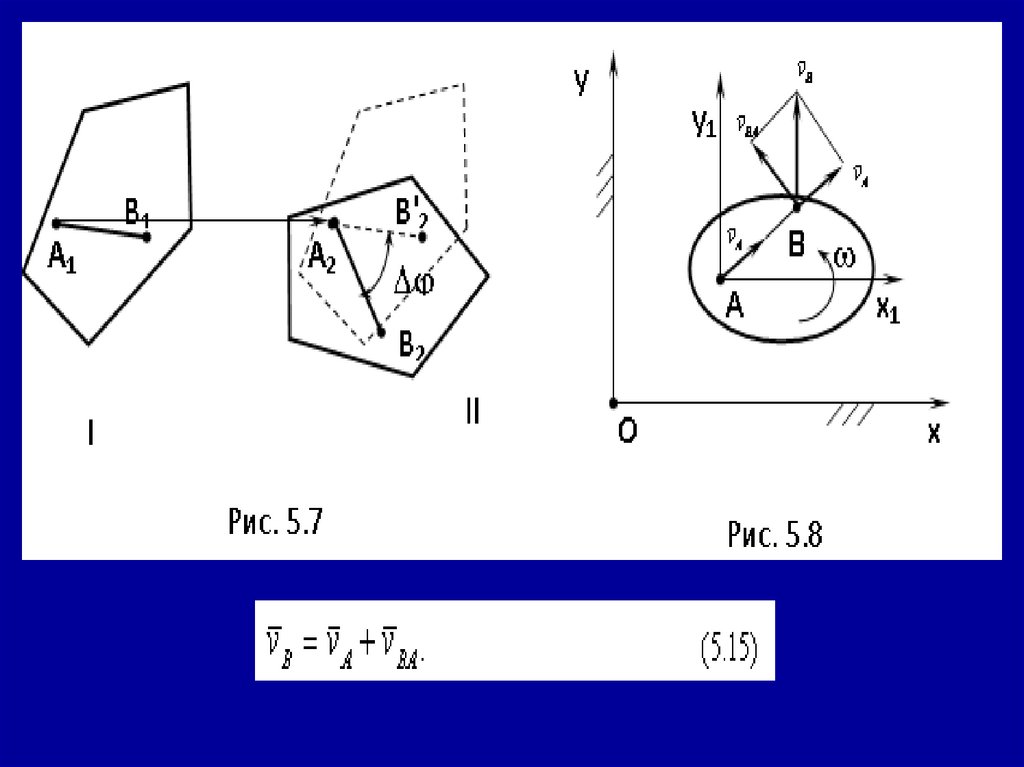
39.
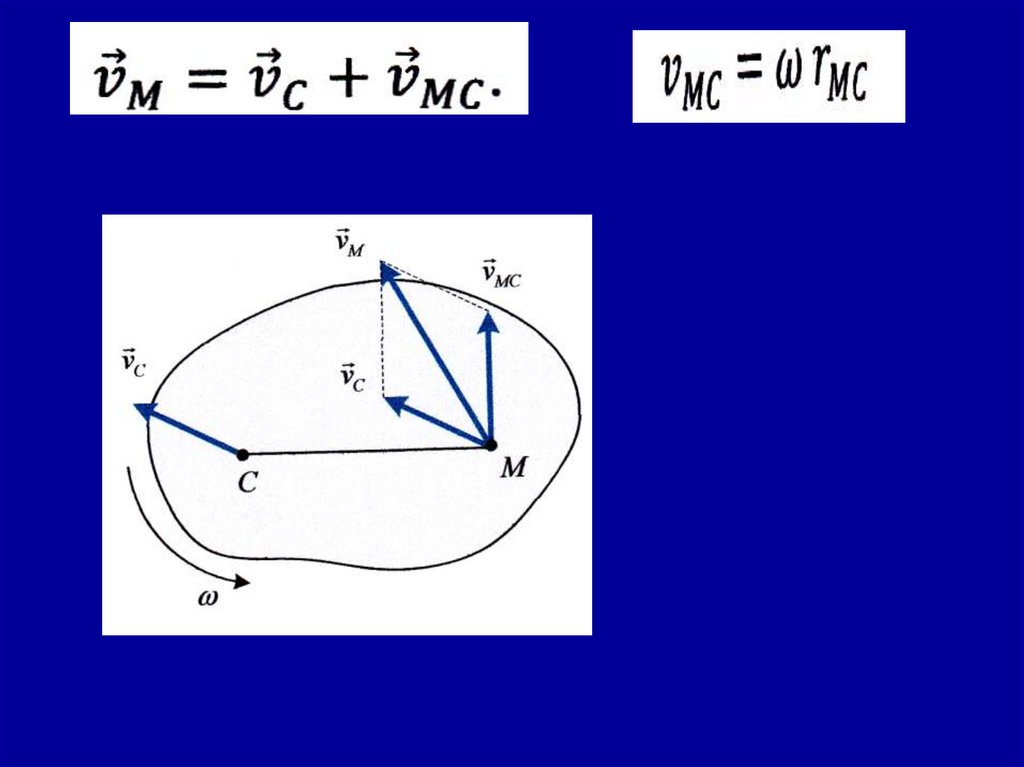
Теорема о сложении скоростей при плоскомдвижении
Скорость точки плоской фигуры равна векторной
сумме скорости полюса и скорости, которая эта точка
имеет в относительном вращении этой фигуры вокруг
полюса:
40.
41.
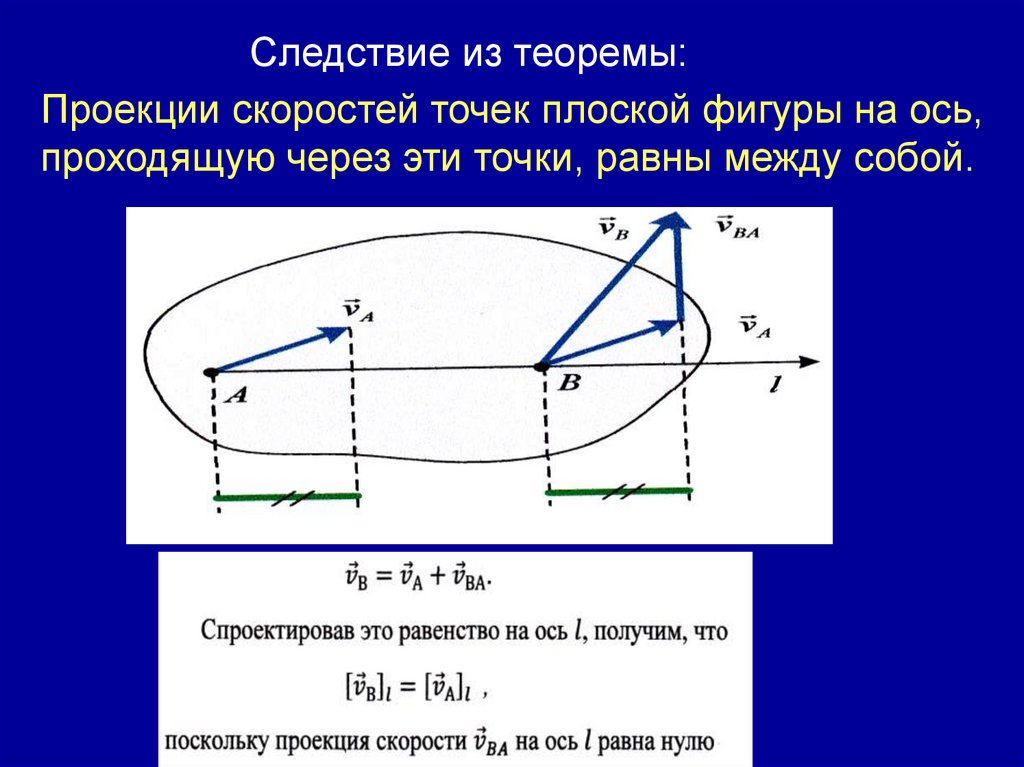
Следствие из теоремы:Проекции скоростей точек плоской фигуры на ось,
проходящую через эти точки, равны между собой.
42.
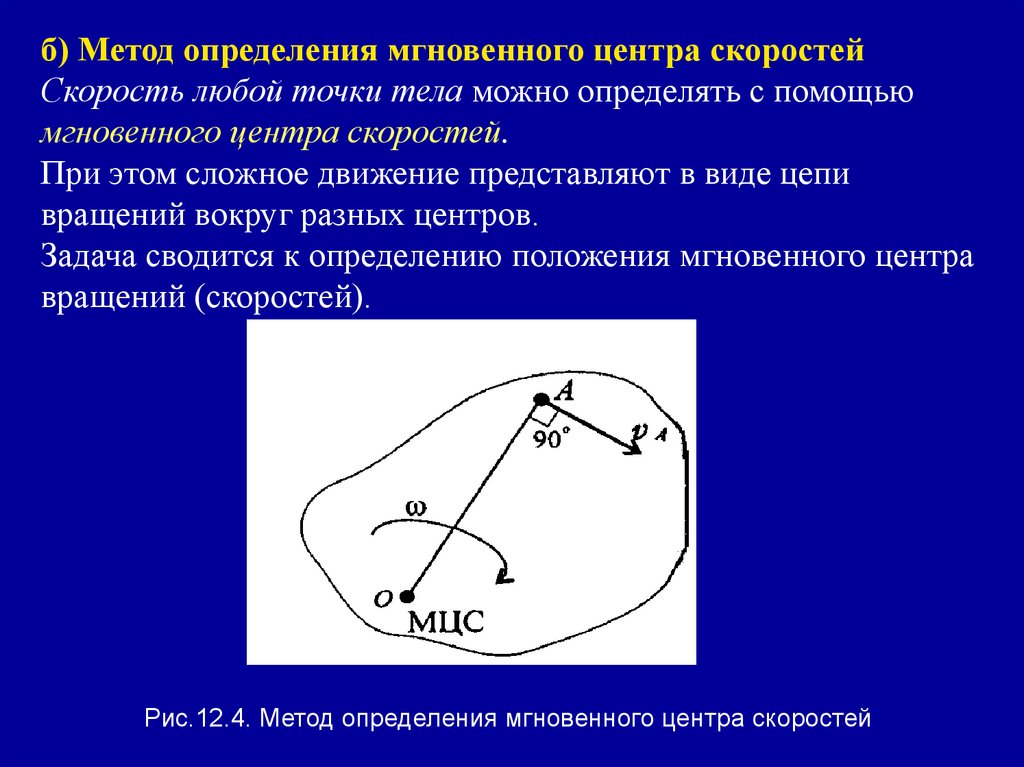
б) Метод определения мгновенного центра скоростейСкорость любой точки тела можно определять с помощью
мгновенного центра скоростей.
При этом сложное движение представляют в виде цепи
вращений вокруг разных центров.
Задача сводится к определению положения мгновенного центра
вращений (скоростей).
Рис.12.4. Метод определения мгновенного центра скоростей
43.
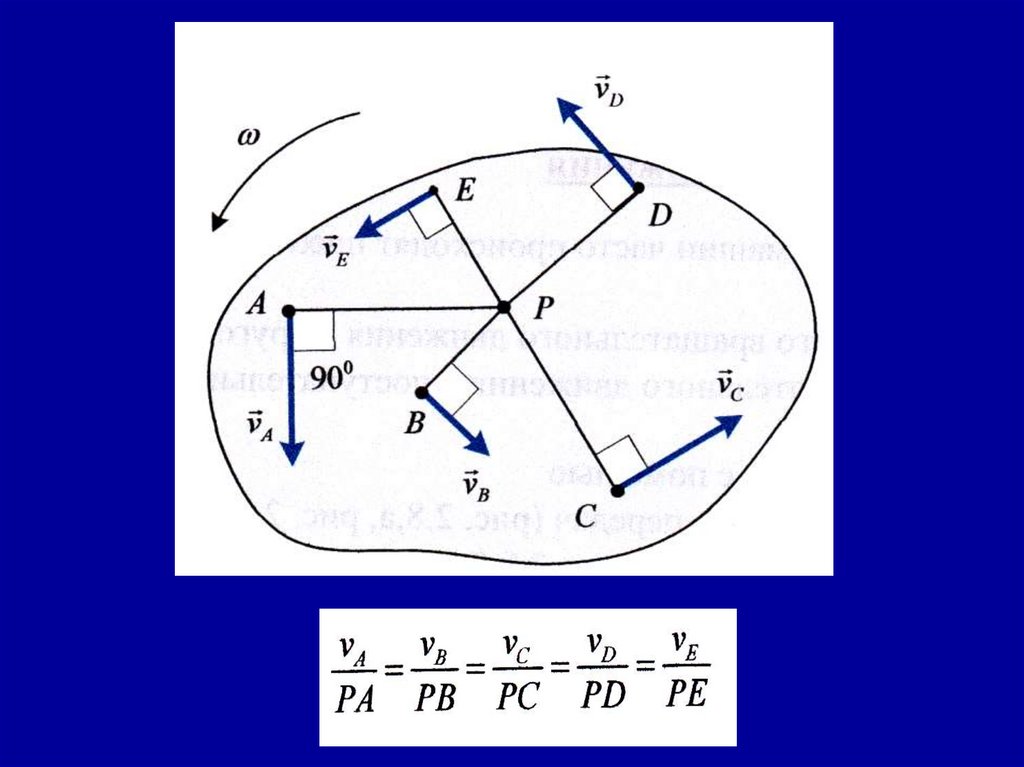
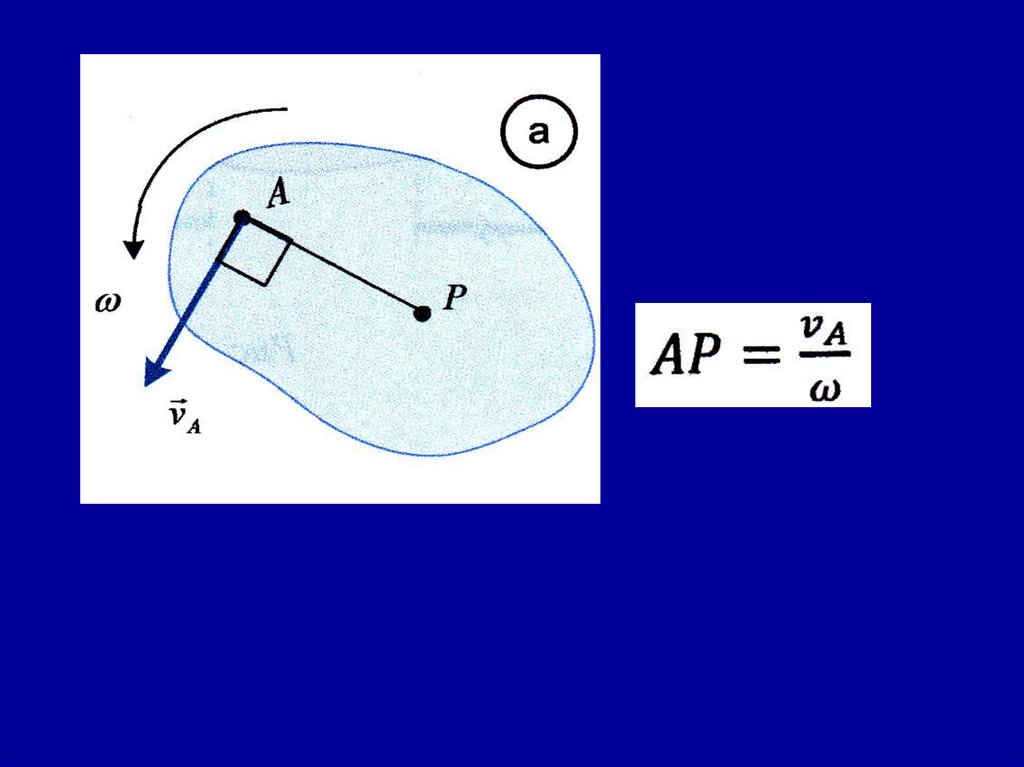
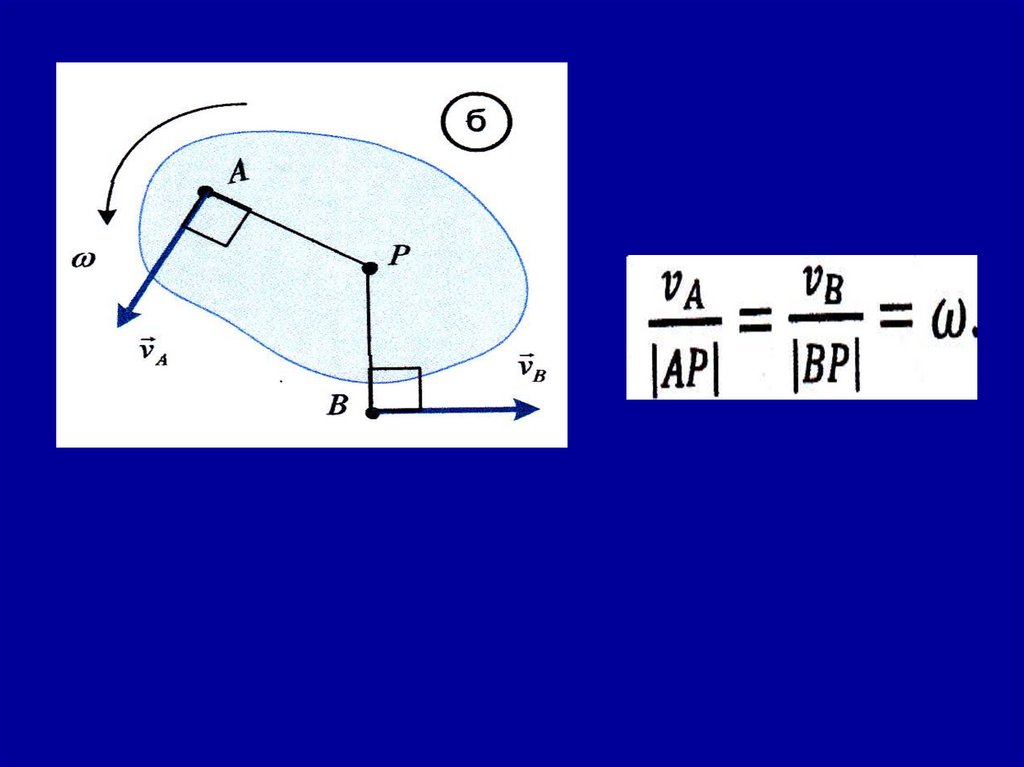
Мгновенным центром скоростей (МЦС) являетсяточка на плоскости, абсолютная скорость которой
в данный момент равна нулю.
Вокруг этой точки тело совершает поворот со
скоростью ω
Скорость точки А в данный момент равна
vA = ωОА,
т.к. vA — линейная скорость точки А,
вращающейся вокруг МЦС.
Существуют три способа определения положения
мгновенного центра скоростей.
44.
45.
46.
47.
48.
49.
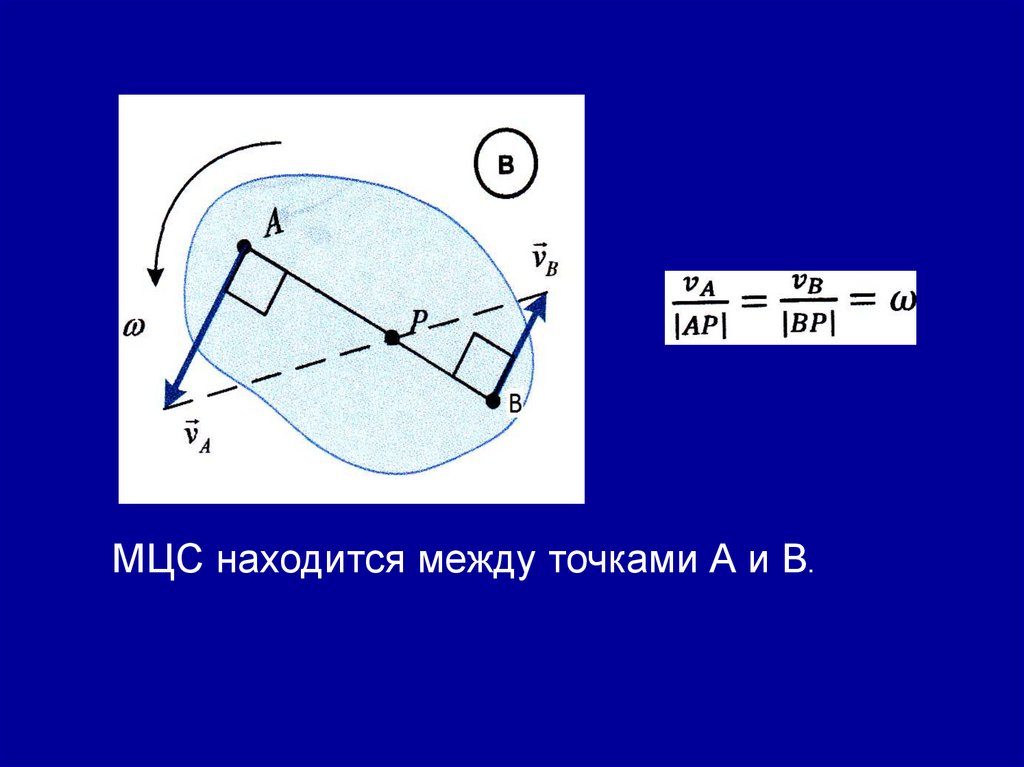
МЦС находится между точками А и В.50.
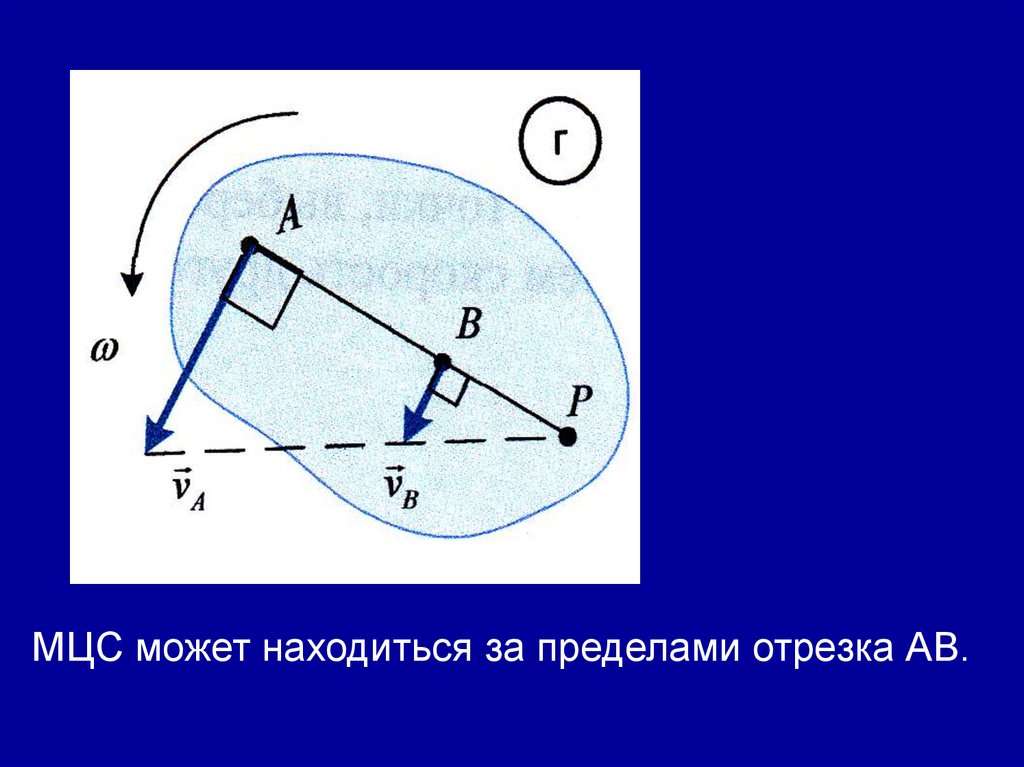
МЦС может находиться за пределами отрезка АВ.51.
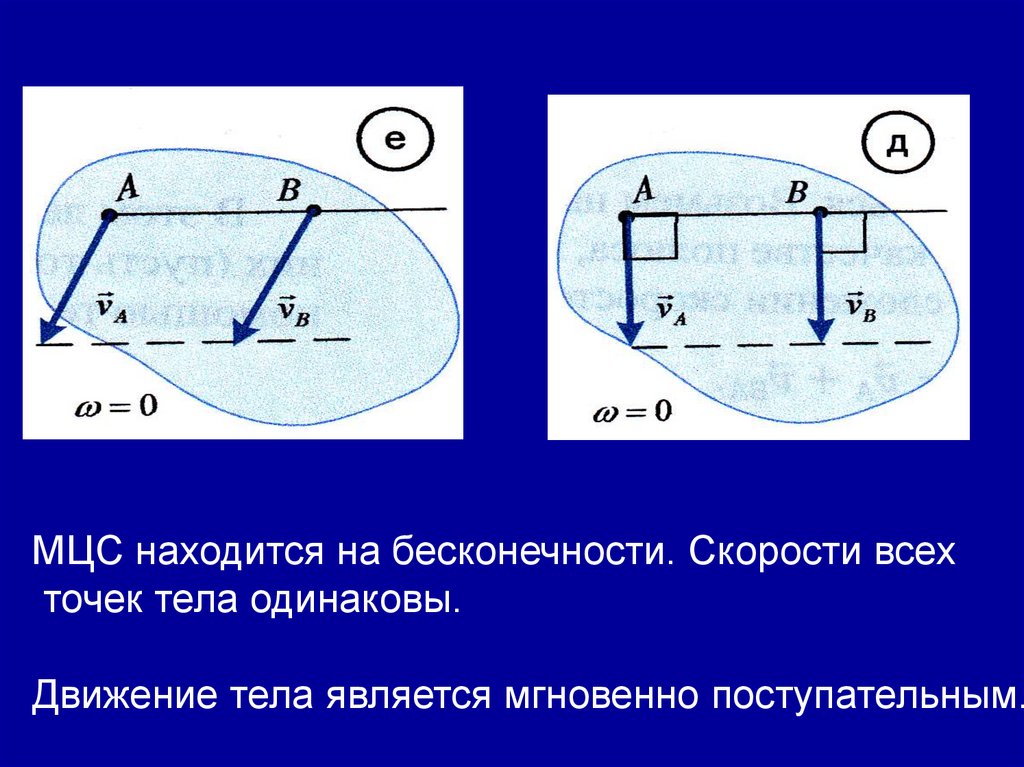
МЦС находится на бесконечности. Скорости всехточек тела одинаковы.
Движение тела является мгновенно поступательным.
52.
53.
54.
55.
56.
57.
58.
59.
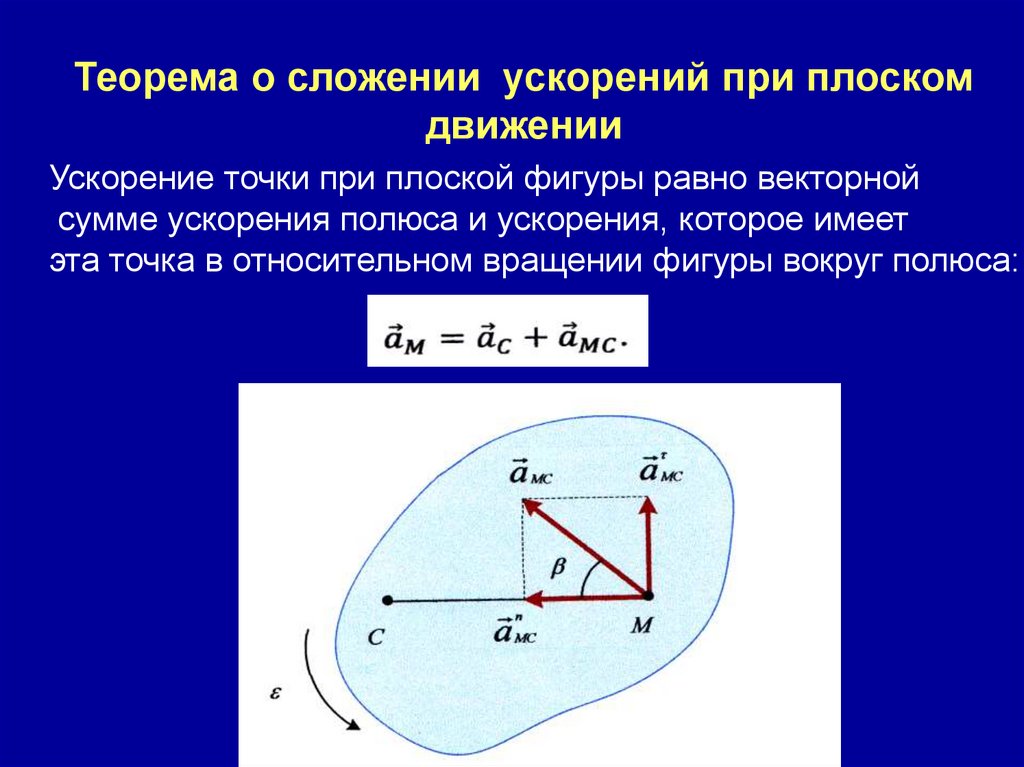
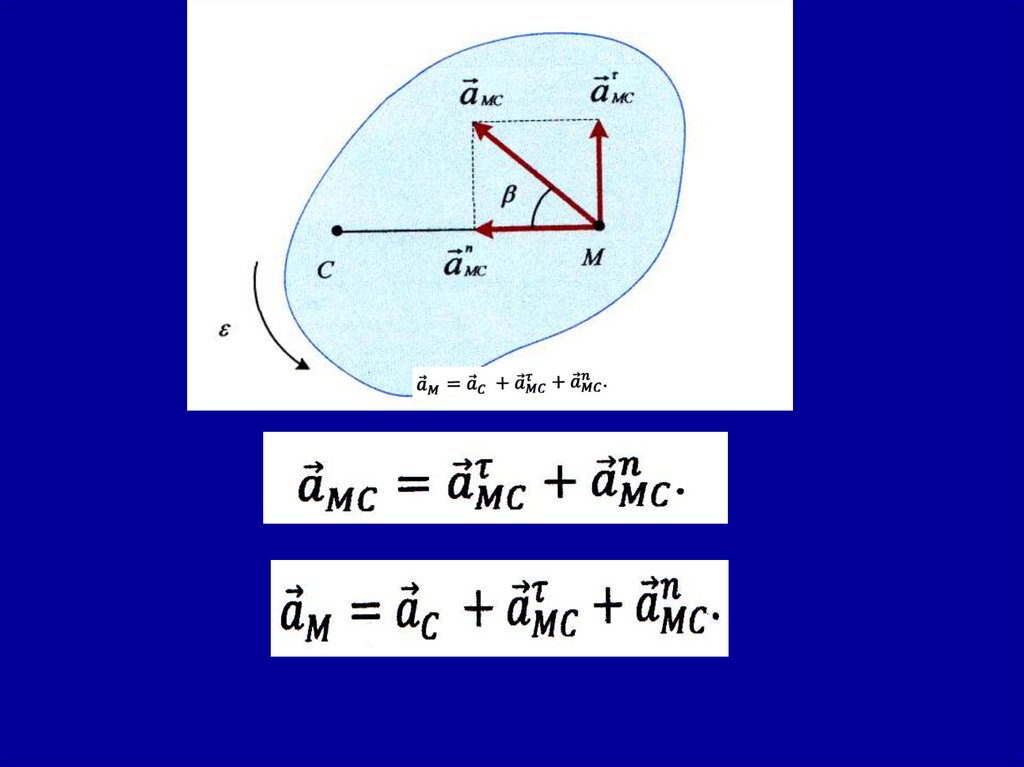
Теорема о сложении ускорений при плоскомдвижении
Ускорение точки при плоской фигуры равно векторной
сумме ускорения полюса и ускорения, которое имеет
эта точка в относительном вращении фигуры вокруг полюса:
60.
61.
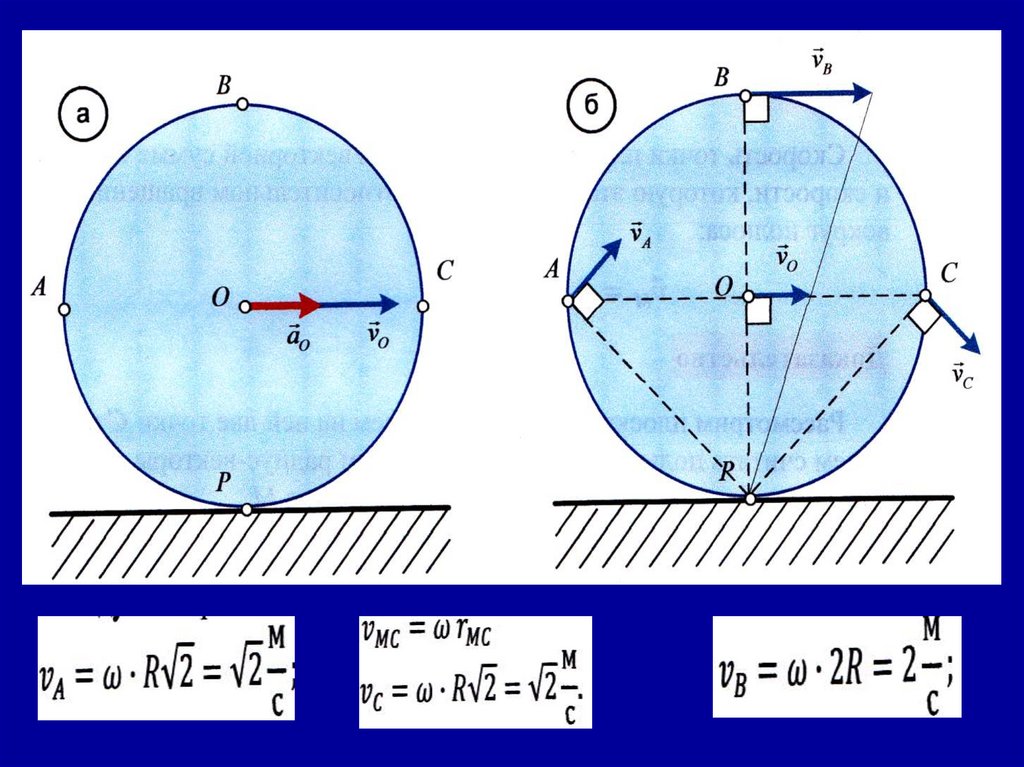
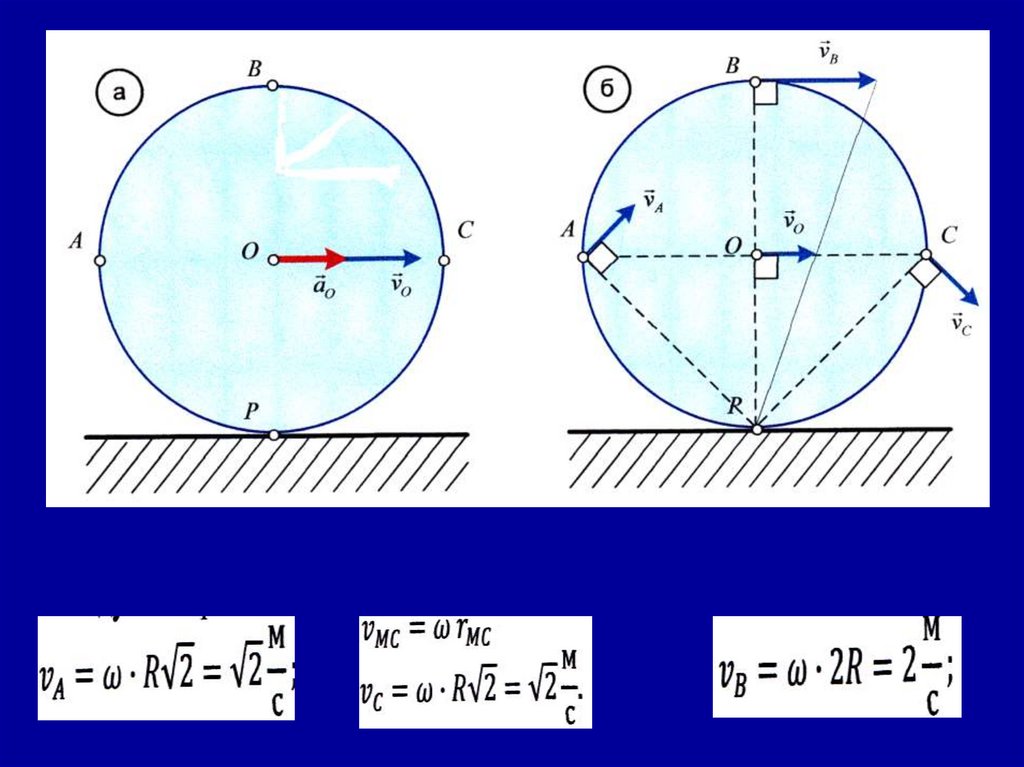
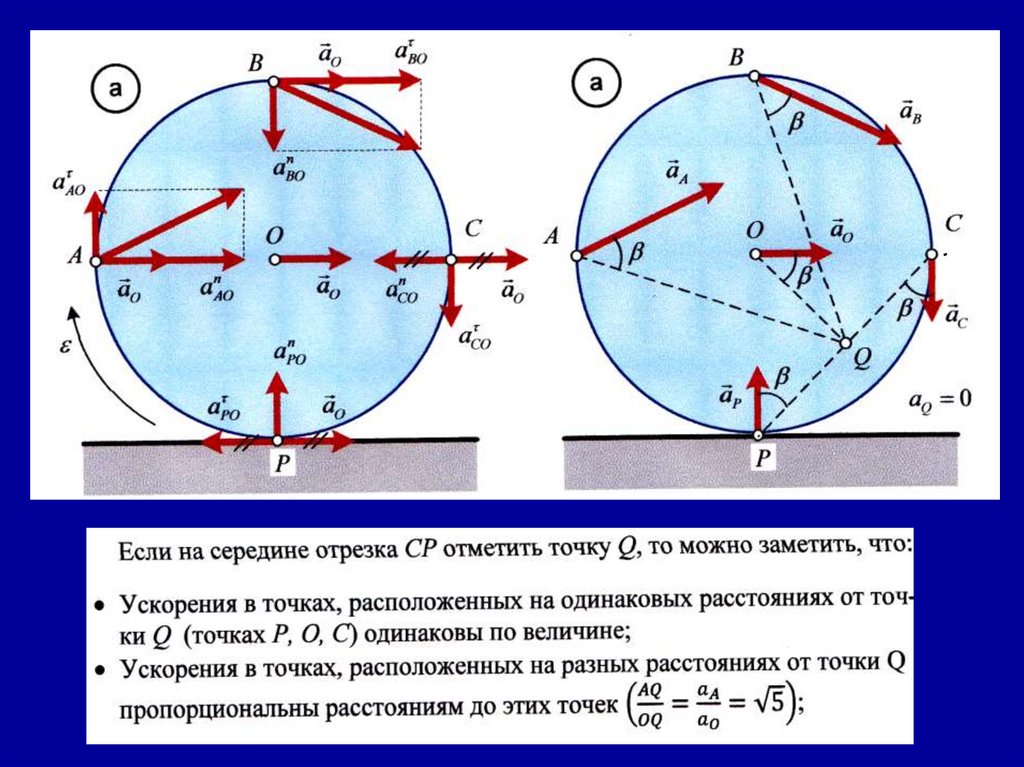
Пусть колесо радиусом R=1 м катится без скольжения по горизонтальной плоскости. Скорость центра ϑₒ=1 м/с, а ускорениецентра колеса по направлению совпадает со скоростью и равно
аₒ=1 v|c ²/.
Определить скорости и ускорения точек А,В,С,Р, расположенных
на ободе колеса.
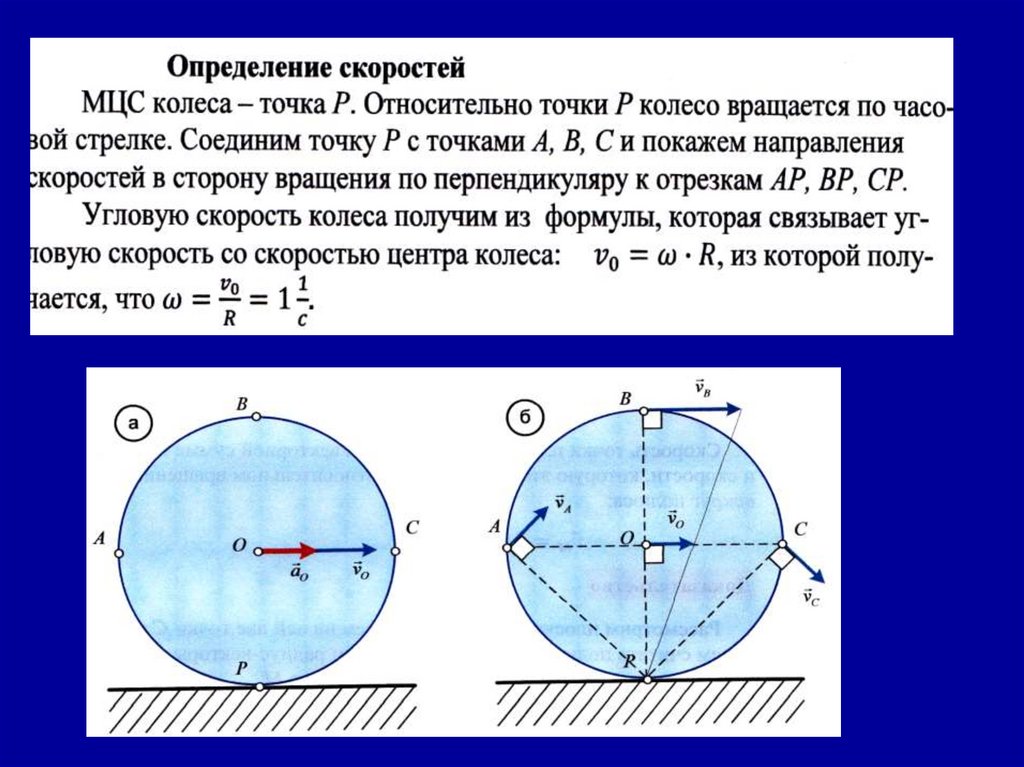
1.Определение скоростей
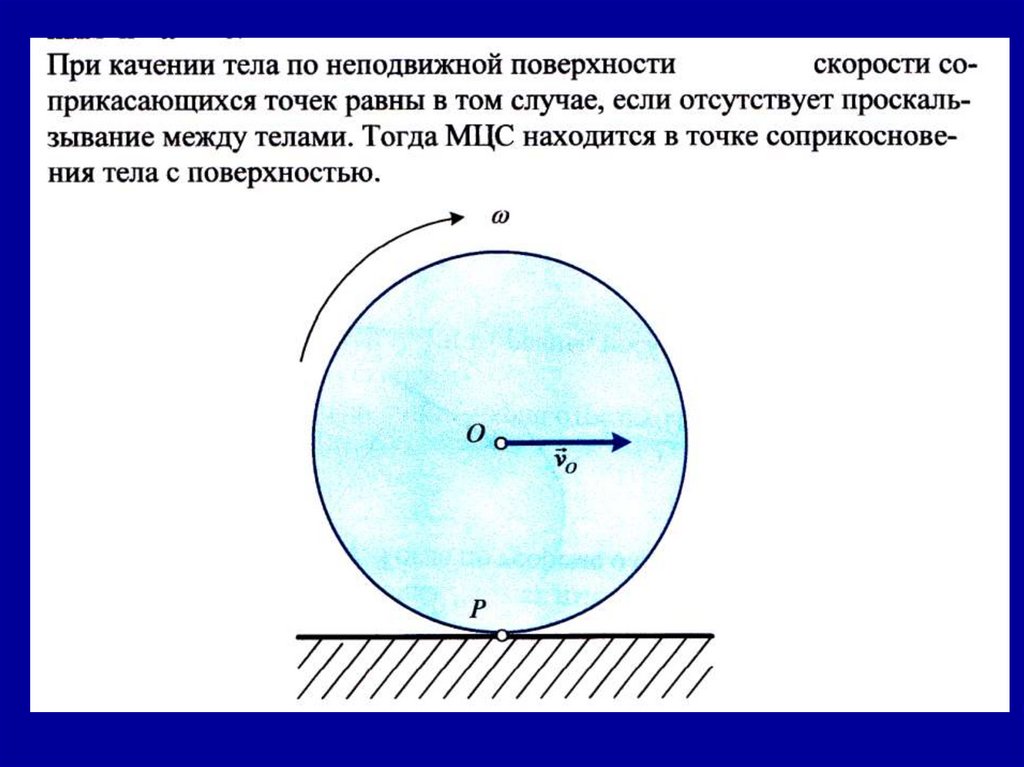
МЦС колеса –точка Р. Относительно точки Р колесо вращается по
часовой стрелке. Соединим точку Р с точками А, В, С и покажем
направления скоростей в сторону вращения по перпендикуляру
к отрезкам АР, ВР,СР.
Угловую скорость колеса получим из формулы, которая связывает
угловую скорость со скоростью центра колес: ϑ ₒ= ѡ ∙ R, из
которой получим ѡ = ϑₒ / R
62.
63.
64.
65.
66.
Ускорения в точках А,В,С,Р направлены таким образом,что составляют одинаковый угол β с отрезками,
соединяющими эти точки с точкой Q;
Ускорение в самой точке Q при этом равно нулю.
Точка тела Q, ускорение которой в данный момент равно нулю,
называется мгновенным центром ускорений.
Существуют правила, по которым всегда можно найти
положение мгновенного центра ускорений (МЦУ), после чего
определение ускорений других точек тела сильно упрощается.
67.
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИДвижение в механике всегда рассматривается по
отношению к какой-либо системе отсчёта. Однако в
некоторых случаях бывает целесообразно или даже
необходимо изучать движение материальной точки (МТ)
относительно двух различных систем отсчёта
одновременно.
Одну из этих систем отсчёта условно считают
неподвижной, базовой, а другую полагают движущейся
относительно первой. Тогда движение точки можно
рассматривать, как состоящее из двух движений: первое —
движение относительно движущейся системы отсчёта,
второе — движение вместе с движущейся системой
относительно неподвижной. Такое движение точки
называют сложным.
68.
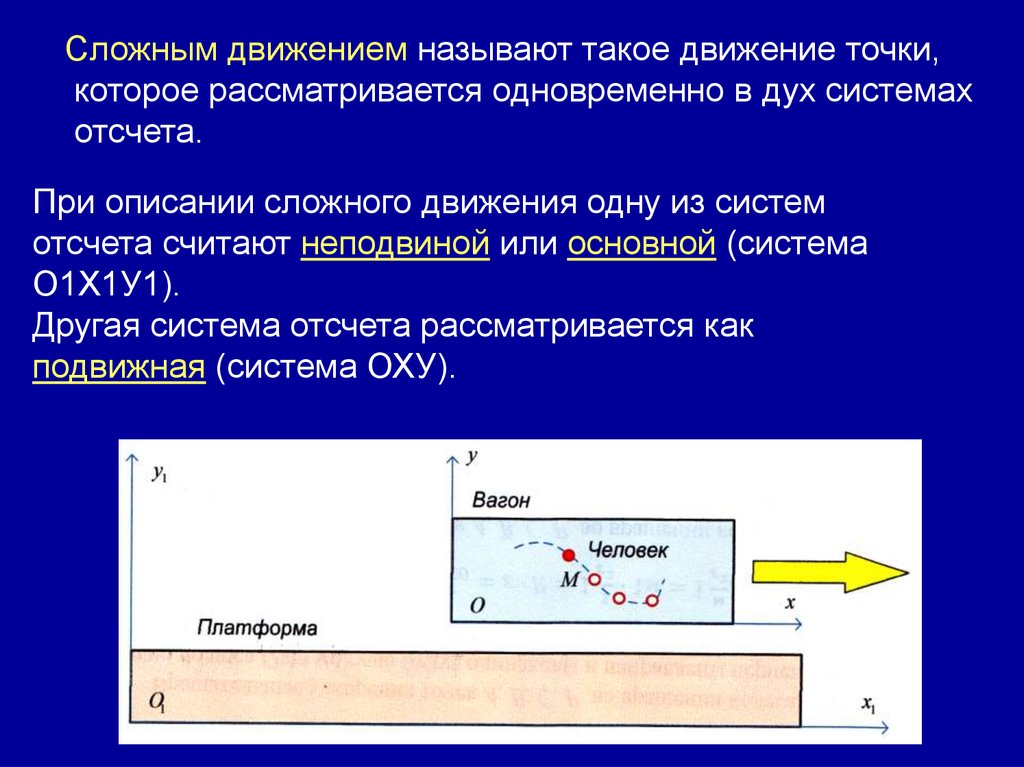
Сложным движением называют такое движение точки,которое рассматривается одновременно в дух системах
отсчета.
При описании сложного движения одну из систем
отсчета считают неподвиной или основной (система
О1Х1У1).
Другая система отсчета рассматривается как
подвижная (система ОХУ).
69.
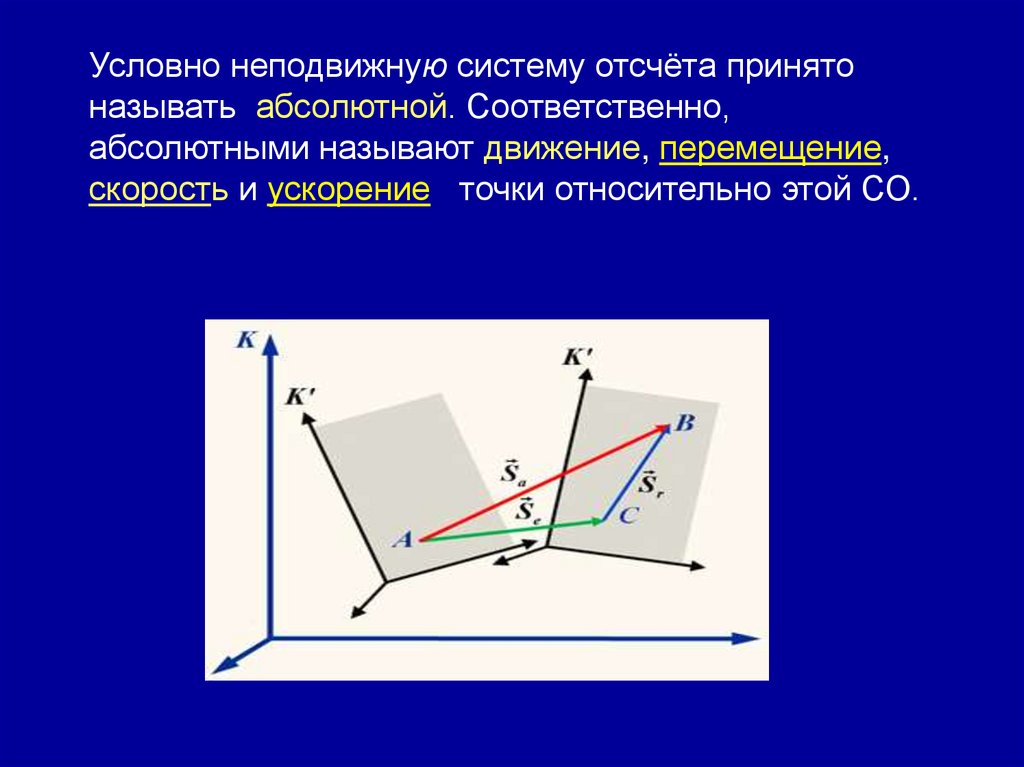
Условно неподвижную систему отсчёта принятоназывать абсолютной. Соответственно,
абсолютными называют движение, перемещение,
скорость и ускорение точки относительно этой СО.
70.
На рисунке система отсчёта K выбрана в качествеабсолютной. Условно подвижную систему отсчёта принято
называть относительной. Движение, перемещение,
скорость и ускорение точки относительно этой системы
также называют относительными.
Система K' на рисунке является относительной.
Движение, совершаемое подвижной системой K' и всеми
жёстко связанными с нею точками пространства относительно системы К, называют перено́сным.
71.
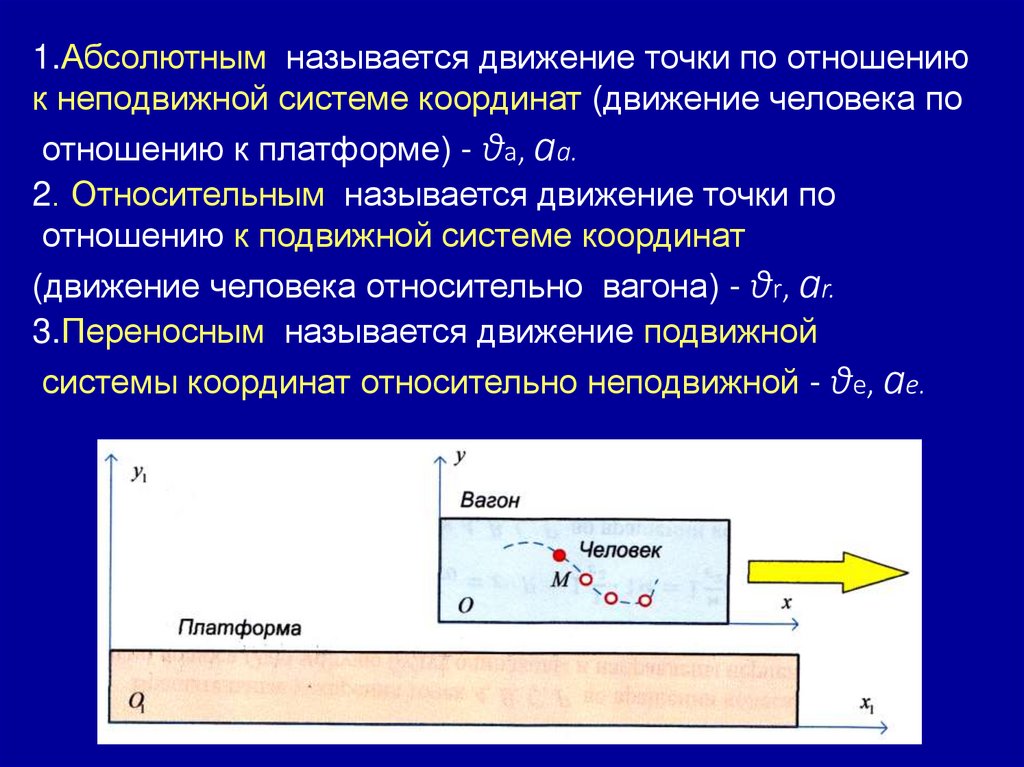
Примером является движение человекавнутри движущегося вагона, в то время как вагон
проезжает мимо неподвижной платформы. Движение
человека можно рассматривать в системе координат
связанной с вагоном, или в системе координат,
связанной с платформой (то есть с Землей).
72.
СЛОЖНОЕ ДВИЖЕНИЕАбсолютное
Переносное
Относительное
73.
1.Абсолютным называется движение точки по отношениюк неподвижной системе координат (движение человека по
отношению к платформе) - ϑа, аа.
2. Относительным называется движение точки по
отношению к подвижной системе координат
(движение человека относительно вагона) - ϑr, аr.
3.Переносным называется движение подвижной
системы координат относительно неподвижной - ϑe, аe.
74.
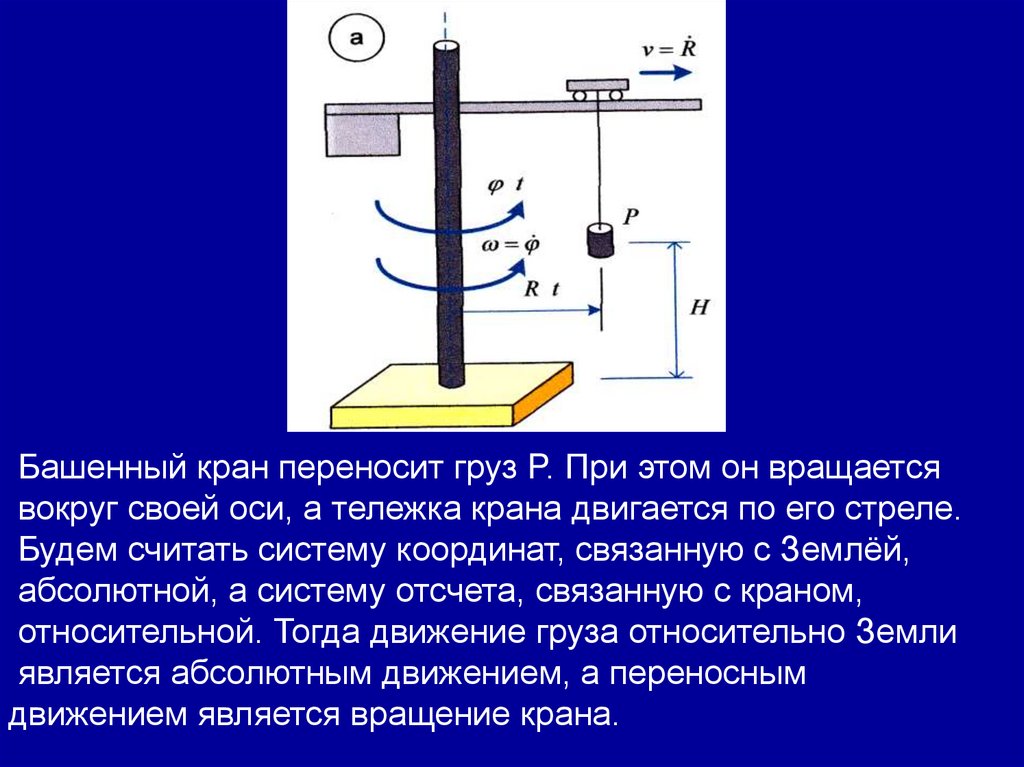
Башенный кран переносит груз P. При этом он вращаетсявокруг своей оси, а тележка крана двигается по его стреле.
Будем считать систему координат, связанную с Землёй,
абсолютной, а систему отсчета, связанную с краном,
относительной. Тогда движение груза относительно Земли
является абсолютным движением, а переносным
движением является вращение крана.
75.
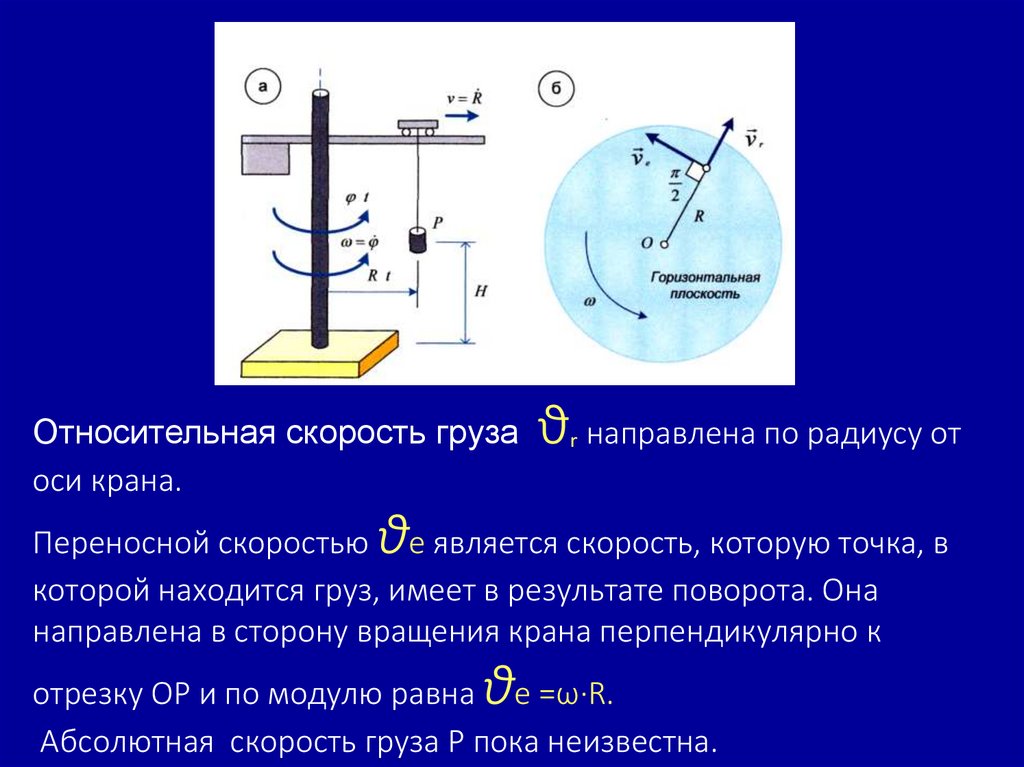
Относительная скорость грузаоси крана.
ϑᵣ направлена по радиусу от
ϑ
Переносной скоростью e является скорость, которую точка, в
которой находится груз, имеет в результате поворота. Она
направлена в сторону вращения крана перпендикулярно к
ϑ
отрезку ОР и по модулю равна e =ѡ∙R.
Абсолютная скорость груза Р пока неизвестна.
76.
СЛОЖЕНИЕ СКОРОСТЕЙ ВСЛОЖНОМ ДВИЖЕНИЙ
77.
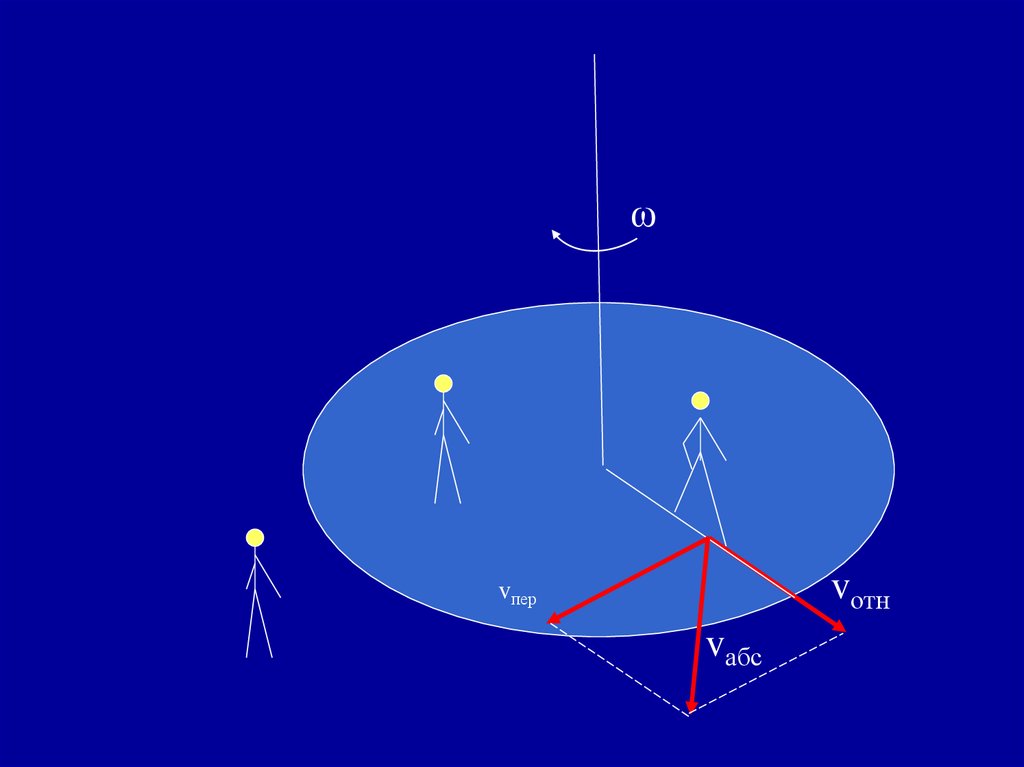
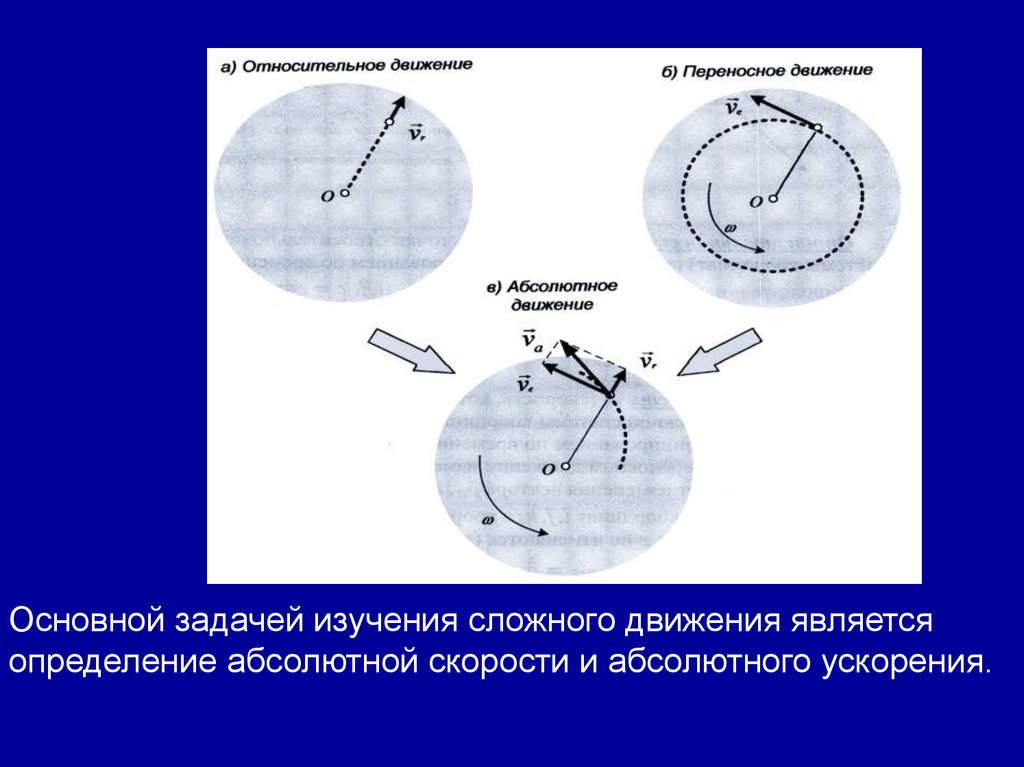
В примере о подъемном кране, траектория относительногодвижения груза есть прямая линия, траектория точки в
переносном движении есть окружность, а траектория
абсолютного движения есть расширяющая спираль.
Абсолютная скорость равна векторной сумме
относительной и переносной скоростей.
ϑ а = ϑr + ϑe
78.
ωvотн
vпер
vабс
79.
Основной задачей изучения сложного движения являетсяопределение абсолютной скорости и абсолютного ускорения.
80.
Гюстав Гаспар Кориолис(Coriolis G.G., 21.05.1792 – 19.09.1843)
Родился в Париже. В 1810 г. окончил
Политехническую школу, а в 1812 г. Школу
мостов и дорог. С 1816 г. начал преподавать
в Политехнической школе, где вскоре стал
профессором, а в 1831 г. – директором
учебной части школы. Преподавал также в
Центральной школе искусств и ремесел и в
Школе мостов и дорог. В 1836 г. был избран
в Парижскую академию наук
81.
Теорема Кориолиса о сложении ускорений.Относительное ускорение получается дифференцированием по
времени вектора относительной скорости.
Переносное ускорение получается дифференцированием по
времени вектора переносной скорости.
Абсолютное ускорение получается дифференцированием по
времени вектора абсолютной скорости.
82.
Абсолютное ускорение точкиравна векторной сумме
относительного переносного и
кориолисова ускорений.
Кориолисово ускорение равно
Удвоенному векторному произведению угловой с корости переносного движения на относительную
скорость точки.
Модуль кориолисово ускорения при этом равен
Из этой формулы видно, что кориолисово ускорение
может быть равно нулю в трех случаях:
83.
1. Когда переносное движение является поступательным(ѡе =0);
2. Когда отсутствует относительное движение (ϑᵣ=0);
3. Когда векторы
и
параллельны друг другу,
то есть когда точка движется вдоль оси.
n
n
aабс aпер
aпер
aотн
aотн
aкор
Направление ускорения Кориолиса определяется по
правилу Жуковского.
84.
Правило Н.Е. ЖуковскогоНикола́й Его́рович
Жуко́вский (5 (17) января
1847 с. Орехово, ныне
Владимирской области –
17 марта 1921, Москва)
85.
Чтобы найти направление кориолисова ускорениянеобходимо:
1. Спроектировать вектор относительной скорости на
плоскость, перпендикулярную оси вращения;
2. Повернуть полученную проекцию на 90° по ходу вращения.
86.
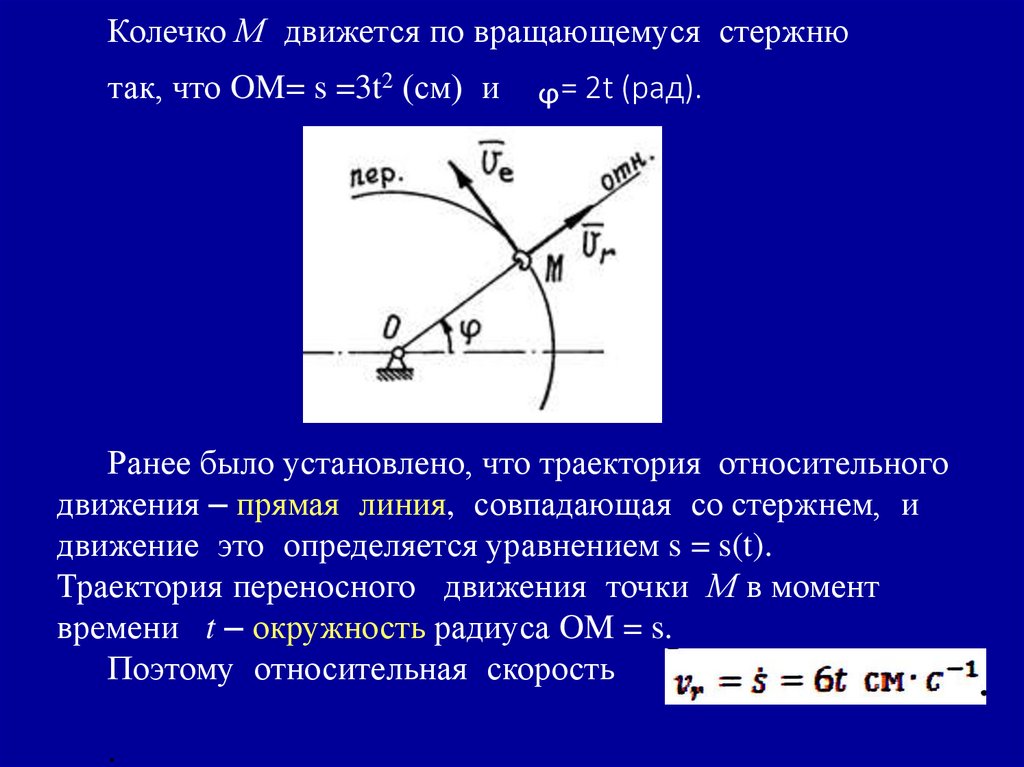
Колечко М движется по вращающемуся стержнютак, что OM= s =3t2 (см) и
ᵩ= 2t (рад).
Ранее было установлено, что траектория относительного
движения – прямая линия, совпадающая со стержнем, и
движение это определяется уравнением s = s(t).
Траектория переносного движения точки М в момент
времени t – окружность радиуса OM = s.
Поэтому относительная скорость
.
87.
И направлена по касательной к траектории вдоль стержня.Переносная скорость колечка, как при вращении вокруг оси,
Направлен вектор этой скорости по касательной к
траектории
переносного
движения,
перпендикулярно
стержню.
Абсолютная скорость колечка
Величина ее, т.к.
88.
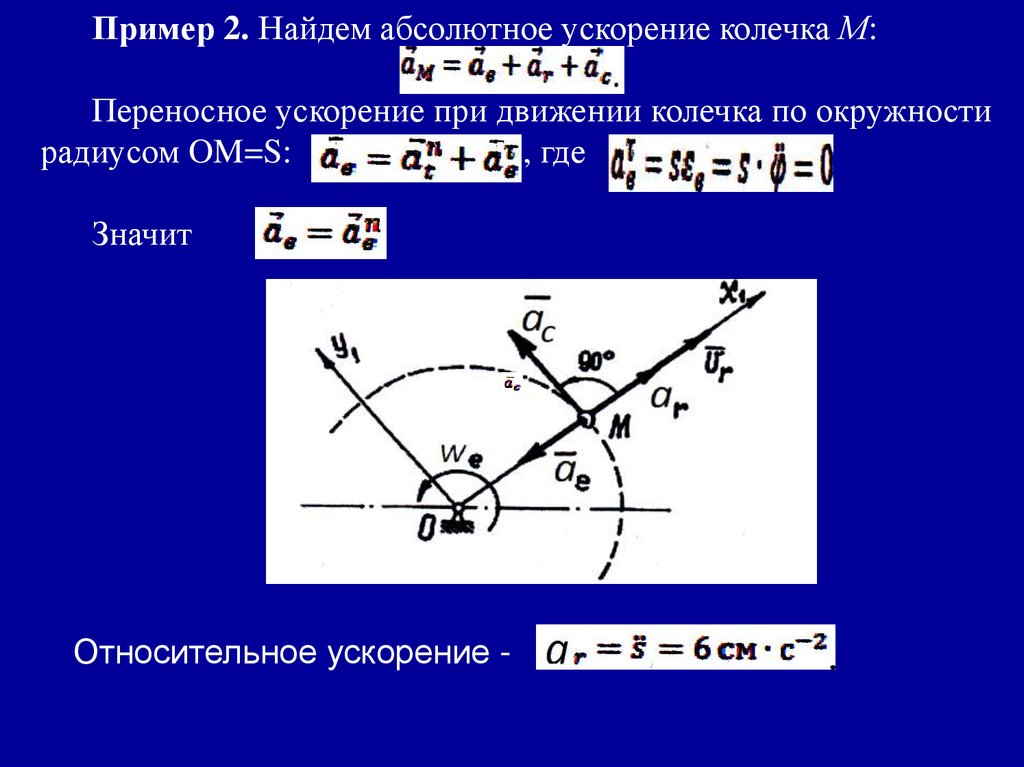
Пример 2. Найдем абсолютное ускорение колечка М:Переносное ускорение при движении колечка по окружности
радиусом OM=S:
, где
Значит
Относительное ускорение -
89.
Ускорение Кориолиса –Вектор
направлен перпендикулярно стержню в сторону
вращения ( по правилу Жуковского).
Величину абсолютного ускорения колечки М найдем с
помощью проекций на подвижные оси Х1 и У1 проектируя
равенство на оси, получим:
Тогда
90.
Примеры проявления Кориолисасилы и Кориолисова ускорения.
91.
Си́ла Кориоли́са — одна из сил инерции, существующаяв неинерциальной системе отсчёта из-за вращения и законов инерции,
проявляющаяся при движении в направлении под углом к оси вращения.
Названа по имени французского учёного Гюстава Гаспара Кориолиса,
Установлен эффект отклонения движущихся объектов во вращающихся
системах.
Причина появления силы Кориолиса — в кориолисовом (поворотном)
ускорении. В инерциальных системах отсчёта действует закон инерции,
то есть, каждое тело стремится двигаться по прямой и с
постоянной скоростью. Если рассмотреть движение тела, равномерное
вдоль некоторого вращающегося радиуса и направленное от центра, то
станет ясно, что чтобы оно осуществилось, требуется придавать
телу ускорение, так как чем дальше от центра, тем должна быть больше
касательная скорость вращения. Это значит, что с точки зрения
вращающейся системы отсчёта, некая сила будет пытаться сместить тело
с радиуса.
Если вращение происходит по часовой стрелке, то двигающееся от
центра вращения тело будет стремиться сойти с радиуса влево. Если
вращение происходит против часовой стрелки — то вправо.
92.
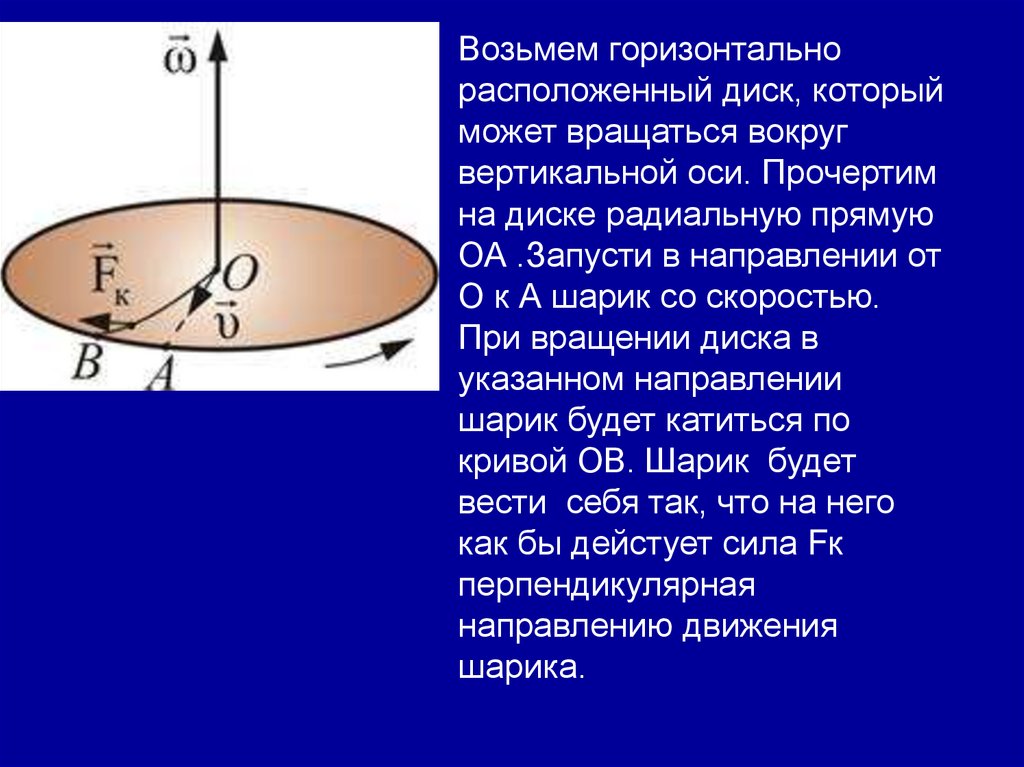
Возьмем горизонтальнорасположенный диск, который
может вращаться вокруг
вертикальной оси. Прочертим
на диске радиальную прямую
ОА .Запусти в направлении от
О к А шарик со скоростью.
При вращении диска в
указанном направлении
шарик будет катиться по
кривой ОВ. Шарик будет
вести себя так, что на него
как бы дейстует сила Fк
перпендикулярная
направлению движения
шарика.
93.
Кориолисово ускорение ощущаетбортпроводница, когда идёт по салону самолёта в
то время, когда он совершает разворот.
Сила Кориолиса, вызванная вращением Земли,
может быть замечена при наблюдении за
движением маятника Фуко.
94.
Кроме того, сила Кориолиса проявляется и вглобальных масштабах. В северном полушарии сила
Кориолиса направлена вправо от движения, поэтому
правые берега рек в Северном полушарии более
крутые — их подмывает вода под действием этой
силы (см. Закон Бэра) . В Южном полушарии всё
происходит наоборот. Сила Кориолиса ответственна
также и за вращение циклонов и антициклонов (см.
геострофический ветер) .
95.
При идеальных условиях сила Кориолиса определяет направлениезакручивания воды в водопроводе — например, при сливе в
раковине. Однако идеальные условия трудно достижимы и
поэтому как в Южном, так и в Северном полушарии воронка в
раковине может закручиваться как по часовой, так и против
часовой стрелки. Это связано с тем, что для данного явления
число России велико, то есть масштаб явления слишком мал,
чтобы на него в значительной степени повлияла сила Кориолиса.
Направление закручивания воды в раковине определяется формой
раковины и конфигурацией канализационной системы в большей
степени, чем силой Кориолиса. Однако, при должной
аккуратности и соответствующих приготовлениях, можно
наблюдать эффект закручивания, обусловленный только лишь
силой Кориолиса, и в домашних условиях - в Северном
полушарии такая воронка будет закручиваться против часовой
стрелки, а в Южном - по часовой.
96.
Таким образом, при выстреле пушки на север из любойточки на экваторе, снаряд падает восточнее своего
первоначально заданного направления. Это
отклонение объясняется тем фактом, что на экваторе
снаряд двигается к востоку быстрее, чем в любой точке
севернее. Аналогично, если стрелять со стороны
северного полюса, то снаряд должен падать правее по
отношению к своей прицельной точке. Так как в этом
случае за время полета цель успевает переместиться к
востоку дальше по причине своей большей, чем у
снаряда, восточной скорости. Аналогичные смещения
происходят при любом выстреле, если только
первоначальная скорость снаряда имеет ненулевую
проекцию на направление север — юг.
97.
Проявление Кориолиса силы при качениимаятника Фуко.
На Северном полюсе сила Кориолиса
направлена вправо по ходу маятника. В итоге
траектория движения маятника будет иметь вид
розетки.
98.
Устройство, наглядно демонстрирующее вращение Земли вокруг своейоси. Изобретение Жаном Фуко (1819
-1868).
Маятник Фуко
является математическим маятником,
плоскость колебаний которого
медленно поворачивается
относительно земной поверхности в
сторону, противоположную
направлению вращения Земли.
Представлена модель маятника Фуко, расположенного
в южном полушарии Земли. Изображенная на анимации
траектория движения соответствует случаю, когда маятник
приводится в движение коротким толчком из положения
равновесия.
99.
Самый простой пример использования силыКориолиса — это эффект ускорения кручения
танцоров. Чтобы ускорить свое вращение,
человек может начать крутиться с широко
разведёнными в стороны руками, а затем — уже
в процессе — резко прижать руки к туловищу, что
вызовет увеличение круговой скорости (согласно
закону сохранения момента импульса). Эффект
силы Кориолиса проявится в том, что для такого
движения руками придётся прикладывать усилия
не только по направлению к телу, но и в
направлении по вращению. При этом возникает
ощущение, что руки отталкиваются от чего-то,
при этом ещё больше ускоряясь.
100.
Траектории шарика придвижении по поверхности
вращающейся тарелки в
разных системах отсчета
(вверху — в инерциальной,
внизу — в неинерциальной,
вращающейся вместе с
тарелкой).
101.
Кориолисова ускорению подвержены движениявоздушных масс, морских течений, течения рек. Это
одна из гл. причин того, что у рек в Сев. полушарии
правый берег размывается интенсивней, он более
крутой, чем левый. Пример – р. Волга, на
значительном протяжении которой зап. берег крутой,
обрывистый, а левый невысокий, низменный.
Впервые объяснил закономерность подмыва берегов
К. М. Бэр, работавший в России в 19 в. (закон Бэра).
102.
Примеры действия Кориолисова ускорения всеверном полушарии:
-отклонение Гольфстрима и других течений,
-отклонение воздушных масс,
-закручивание против часовой стрелки циклонов,
-реки подмывают правый берег,
-правый рельс на железных дорогах изнашивается быстрее.
В южном полушарии Кориолисова ускорение имеет обратное
направление, поэтому перечисленные эффекты проявляются
зеркально по отношению к северному полушарию.
103.
При движении тела на север Кориолисова ускорение направленона запад.
При движении тела на юг Кориолисова ускорение направавлено
на восток.
При движении тела на восток Кориолисово ускорение направлено к
земной оси.
При движении тела на запад Кориолисова ускорение направлено
от земной оси.































































 physics
physics








