Сложение и умножение неравенств. Тема 4

1.

№ 50 (2, 4)
2)
2 ,3 a 4 , 6 / 2 ,3
a 2
4)
3
1
3
x / ( )
4
3
4
4
x
9
Проверка д/з

2.

№ 52 (2, 4, 6)
a b
2) a b / 0,19
0,19a 0,19b
1
)
4) a b / (
6
1
1
a
b
6
6
a
b
6
6
Проверка д/з
6) a b / 5,2
2
a 5,2 b 5,2 /
3
2
2
(a 5,2) (b 5,2)
3
3

3.

№ 54 (2, 4)
Проверка д/з
2) ( x 1 )( x 8 ) ( x 2 )( x 4 )
x2 x 8x 8 x2 2x 4x 8
x
2
x 8x x
2
2x 4x 8 8
5 x 0 / ( 5)
x 0
4) ( x 3 )( 3 x ) ( x 2 ) 2
x
2
9 x
2
4 x 4
x 2 x 2 4 x 9 4
4 x 13 / ( 4 )
13
x
4

4.

1. На основании какого свойства неравенств можно
утверждать, что если х < у , то:
15х < 15у , - 9х > - 9у,
х + 20 < у + 20 ?
2. Известно, что а > 5 . Следует ли из этого, что:
а) разность а - 5 – положительное число;
б) разность а - 6 – положительное число;
в) разность а - 4 – положительное число?
3. Расположите в порядке убывания числа:
1
1
11
2,6; 3,8; 2 ; 3 ; 2
3
7
12
-21
3
- 2,6
11
-2
12
-31
7
- 3,8

5.

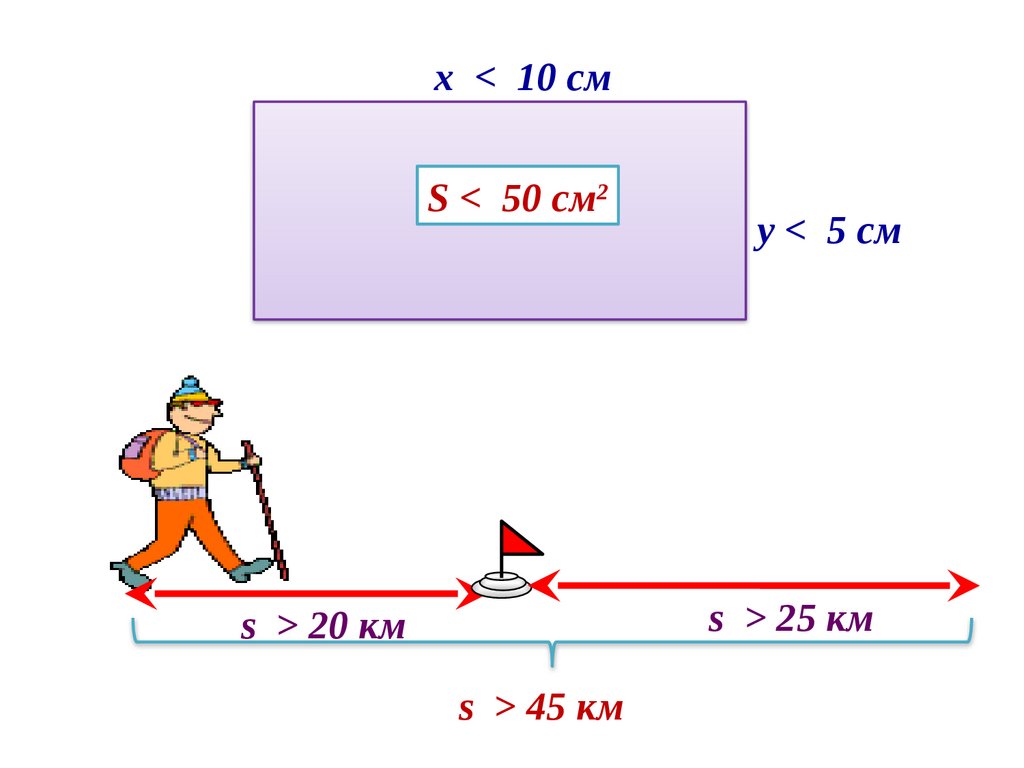
х < 10 см
S < 50 см2
у < 5 см
s > 25 км
s > 20 км
s > 45 км

6.

§4. СЛОЖЕНИЕ И УМНОЖЕНИЕ
НЕРАВЕНСТВ
Теорема 1. При сложении неравенств одинакового знака
получается неравенство того же знака:
если a > b и c > d , то a + c > b + d .
a>b
+ c>d
Пример:
a)
2 < 5,5
+
5<7
7 < 12,5
б)
- 3 > - 7,2
+
0,5 > 0
- 2,5 > - 7,2
a+c>b+d

7.

Теорема 2. При умножении неравенств одинакового
знака, у которых левые и правые части положительны,
получается неравенство того же знака:
если a > b и c > d и a , b, c, d – положительные числа,
то ас > bd .
Пример:
a)
2<3
х
5<7
б)
7,05 > 1,2
х
10 > 5
10 < 21
70,5 > 6
Пример: Доказать, что если а, b – положительные числа и
а > b, то а2 > b2.
а>b
х а>b
если а, b – положительные числа
п
п
и
а
>
b,
то
а
>
b
а2 > b2
при любом натуральном п
Из 5 > 3 следуют неравенства 56 > 36, 59 > 39 и т.д.

8.

В классе: № 59 (устно), 60, 61, 62 (1, 3, 5), 63,
65 (1, 3), 66 (1, 3, 5), 67
№ 62 (1; 3; 5)
а > 2, b > 5
1) 3а + 2b > 16 а > 2/*3
b > 5/*2
3а > 6
+
2b > 10
3а + 2b > 16
ч.т.д.
2
3) а2 + b2 > 29 а > 2/^2
а
+ 2 >4
b > 25
b > 5/^2
ч.т.д.
а2 + b2 > 29
а>2
а+b>7
5) (а + b) 2 > 35
+
х а+b>7
b>5
2
(а
+
b)
> 49 тем более > 35
а+b>7
ч.т.д.

9.

х < 7
3см
№ 63
у
<
1м
Р < 3 м?
15
см
х < 73см
+ у < 1м 15см
с < 1м 11см
х + у + с < 2м 99 см
Р < 2м 99 см , тем более < 3м
с < 1м 11см
№ 65 (1; 3)
а < 2, b > 3
а < 2, 3 < b
1) а + 3 < b + 2
а<2
+
3<b
а + 3 < b + 2 , ч.т.д.
3) b – 3 > а – 2
а – 2 < b – 3 , или b – 3 > а – 2 , ч.т.д.
В классе: № 59 (устно), 60, 61, 62 (1,3,5), 63, 65 (1,3), 66 (1,3,5), 67

10.

№ 66 (1; 3; 5) а > 2, b > 3, с > 1
а>2
+ b>3
с>1
1) а + b + с > 6
а + b + с > 6 , ч.т.д.
3) 2аb + 3аbс > 30
а>2
3а > 6
а>2
3а > 6
х b>3
с>1
3аbс > 18
2а > 4
2а > 4
х
b>3
2аb > 12
+
3аbс > 18
2аb > 12
2аb + 3аbс > 30 , ч.т.д.
В классе: № 59 (устно), 60, 61, 62 (1,3,5), 63, 65 (1,3), 66 (1,3,5), 67

11.

№ 66 (1; 3; 5) а > 2, b > 3, с > 1
5) а + аb + аbс 2 > 13
аb > 6
х 2
с >1
аbс2 > 6
а>2
а>2
х
b>3
аb > 6
с >1
с2 > 12
с2 > 1
+ аb > 6
аbс2 > 6
а + аb + аbс 2 > 14 , тем более > 13 , ч.т.д.
В классе: № 59 (устно), 60, 61, 62 (1,3,5), 63, 65 (1,3), 66 (1,3,5), 67

12.

в3р
№ 67
3х > 21 см
Р > 56 см
аза
бол
ьш
е
х > 7 см
Р = 2(3х + х) > 56
P = 8x > 56
3х > 21 см
+
х > 7 см
4х > 28 см | ∙ 2
8х > 56 см , ч.т.д.
В классе: № 59 (устно), 60, 61, 62 (1,3,5), 63, 65 (1,3), 66 (1,3,5), 67

13.

Домашнее задание:
§ 4, № 62 (2, 4, 6), 64,
65 (2, 4), 68