Similar presentations:
Свойство умножения
1.
Мало что-то изобрести – нужно ещёчтобы кто – нибудь оценил
изобретение…
(Кароль Ижиковский)
Критиковать автора легко, но трудно
его оценить.
(Люк де Клапье Вовенарг)
Каждому слову – своя оценка.
(Владимир Борисов)
2.
Свойствоумножения, Способ
Р
разложения
используемое
а
ж д е с Значение
т на
в о
прит омногочлена
ппеременной,
умножениемножители
рпри котором
одночлена на
е уравнение
Слагаемые,
многочлен
обращается
д
в
Равенство,
имеющие одну и
н о г о ч л е н верное
верноем при
р
л равенство
ту же буквенную
любых
у
и
часть
п
т
значениях
Выражение,
п
е
к о э ф ф и ц и е н
переменных
и
л
о
представляющее
Числовой
р
ь
р
собой
сумму
множитель
у
п о д о б н ы е
одночленов
одночленов
в
о
н
к
и
е
ь
т
3.
ас
2
0,6
2
7 х
2
n
3
2
3
3
2
3аb
а с
2
с 2
4 ху
а с
ас
х 36
6аk
а с
2ах
2
2
2
2
2
3
3
4.
72
0, 3
0,1
4 х
2
2
3
1
2
3а
2 3
3
2
1
3
2
5.
Представить в видекуба
квадрата
2
2
2m
4m ___
1
27
,3а
0,09а 0___
4
2 2
1
3
___
3
3
3
3
1 2 2
аb 2 0,008р ___
0
,
2
р
2 а b ___
2
4
5
х
125
х
___
11х у
121х у ____
6 8
3 4
2
6
2 3
6.
Замените * одночленом так,чтобы получившееся равенство
было тождеством
10
2
100 40m 4m
2a 2a 4a
x 4 x
2
2
9b
4 x 16
2
2
2m
3b
x3, 64
7. Формулы сокращённого умножения
Квадрат суммы и разностидвух выражений:
(а-b)2=a2-2ab+b2
(а+b)2=a2+2ab+b2
8. Формулы сокращённого умножения
Разность квадратов:2
2
a -b =(a-b)(a+b)
9. Формулы сокращённого умножения
Сумма и разность кубов:а3-b3=(a-b)(a2+ab+b2)
а3+b3=(a+b)(a2-ab+b2)
10.
Полезные формулыa b a b
а b b а
2
2
2
а b a b
2
2
2
11.
В М Н ДЕ Ф П У К
И О Л С Т
12. Упростите выражения и расшифруйте фамилию математика.
1) (xy-1)(xy+1)2) 16a2-24a+9
3) x2-4xy+4y2
4) 4x2-28xy+49y2
5) (3m-4n)(3m+4n)
6) 1-2b+b2
(Л) (2x-7y)2
(И) 9m2-16n2
(Д) (1-b)2
(Е) x2y2-1
(К) (x-2y)2
(В) (4a-3)2
13.
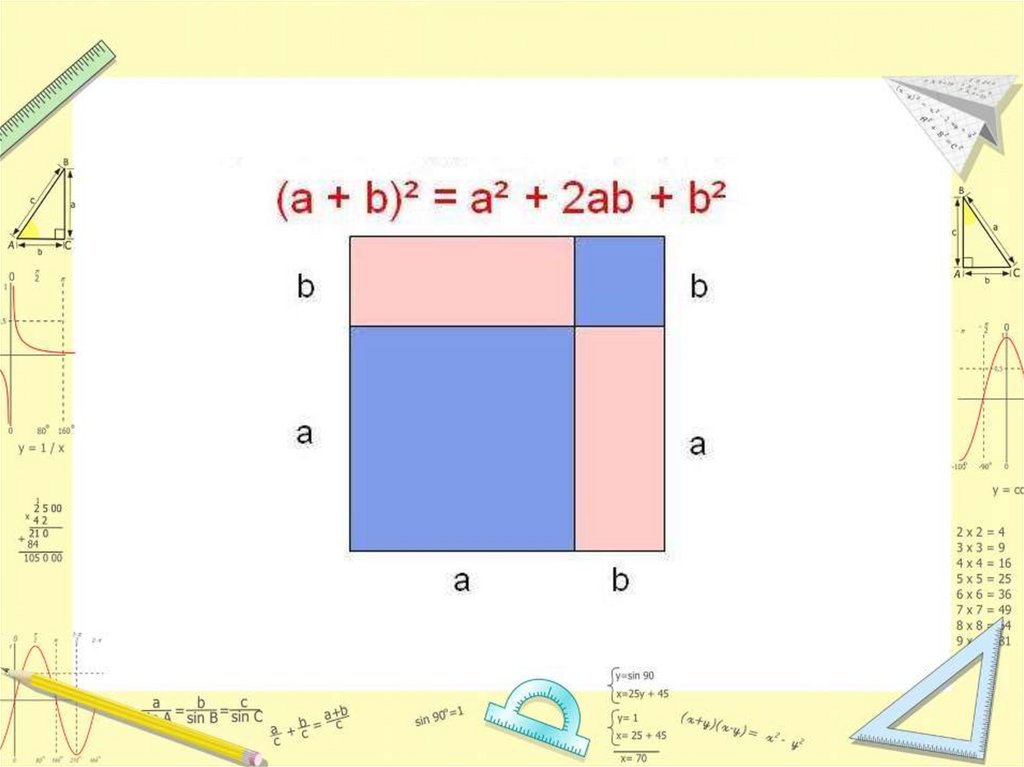
ЕВКЛИДдревнегреческий математик,
живший на рубеже IV-III вв. до н. э.
автор знаменитого трактата
«Начала», посвящённого
элементарной геометрии и теории
чисел. В «Началах» Евклид
геометрически доказал
справедливость равенства
(a + b)² = а² + 2аb +b2
при положительных
значениях а и b
14.
15.
16.
Мало что-то изобрести – нужно ещёчтобы кто – нибудь оценил
изобретение…
(Кароль Ижиковский)
Критиковать автора легко, но трудно
его оценить.
(Люк де Клапье Вовенарг)
Каждому слову – своя оценка.
(Владимир Борисов)
17. Цель урока: Научиться оценивать свою деятельность при решении задач с использованием формул сокращённого умножения. План урока:
1.Вспомним формулы сокращённого умножения;2.Потренируемся в решении задач на применение
этих формул;
3.Сконструируем собственные модели для решения
задач;
4.Будем учиться оценивать свою деятельность.
18. Я задумала два одночлена, нашла их сумму, нашла их разность, перемножила полученные выражения и получила результат: 4х2 – 9у2
ОтгадайтеЯ задумала два одночлена, нашла их сумму,
нашла их разность, перемножила полученные
выражения и получила результат:
2
4х
–
2
9у
Какие одночлены я задумала?
Как вы узнали?
Какую формулу вы использовали?
Сформулируй ее.
19.
ФИЗКУЛЬТМИНУТКА20. 1. Упражнения для улучшения мозгового кровообращения
«Наклоны головы»Вперед
– назад
Вправо
- влево
21. 2. Упражнение общего воздействия
«Бокс»22. 3. Упражнения для снятия утомления с плечевого пояса и рук
«Рывки руками»«Сжимание
кисти в кулак»
23. 4. Упражнение для снятия напряжения с мышц туловища
«Наклоны в сторону»24. «Вращение глазами»
5. Упражнения для глаз«Вращение глазами»
по часовой стрелке
против часовой стрелки
25. «Пальчик»
Приближайте иотводите палец
26. «Во все стороны»
Двигайте глазамивверх-вниз
вправо-влево
27. «Кто там?»
Зажмурьтесь посильнееШироко откройте глаза
28. «Моргание»
29. «Сон»
Закройте глаза30. Отгадывание задуманного числа.
• Задумайте число ;• Умножьте его на себя;
• Прибавьте к результату
задуманное число;
• К полученной сумме
прибавьте 1;
• К полученному числу
прибавьте задуманное
число.
• Решение:
x² + x + 1 + x =
=x² + 2x + 1 =
= (x + 1)²
• Например:
5·5 + 5 + 1 + 5 = 36
36=62
• Скажите мне число,
которое у
тогда
вас получилось и я
отгадаю,
x = 6 – 1 = 5.
какое число вы задумали.
31.
• Задача Пифагора:Докажите, что всякое нечетное число,
кроме единицы, есть разность двух
квадратов.
• 1 способ.
(n+1)2 – n2 = (n+1-n)(n+1+n) = 2n + 1
нечётное число.
• 2 способ.
(n+1)2 – n2 = n2 + 2n + 1 - n2 = 2n + 1
нечётное число.
32. Задача «Эрудит»
• Любое натуральноечисло, оканчивающееся
цифрой 5, можно
записать в виде 10а + 5.
• Например, 25 = 2·10 + 5.
• Доказать, что для
вычисления квадрата
такого числа можно к
произведению а(а + 1)
приписать справа 25.
• Например, 25² = 625,
т.к. 2 ·(2 + 1) = 6.
Доказательство:
(10а + 5)² =
=100a² + 100a + 25 =
=100a(a +1) + 25 =
=a (a +1) ·100 + 25.
Найдите по этому
правилу
45², 75², 115².
33. РЕФЛЕКСИЯ
• Что нового каждый из нас узнал на уроке?• Что каждый из нас делал сегодня на занятии?
• Что было главным? Каковы основные
результаты?
• Какая цель была нашего урока? Достигли ли
мы цели?
• Красный жетон – «5»
• Зелёный жетон – «4»
• Жёлтый жетон – «3»
34. Домашнее задание: 1.Составьте (или подберите из дополнительных источников) задачи, при решении которых используются формулы
сокращённого умножения.На «5» - три задачи
На «4» - две задачи
На «3» - одну задачу
2.Подумайте, какие составляющие вашей
деятельности необходимо изменить, чтобы улучшить
результат? Проработайте задания из классной
работы, при выполнении которых возникали
трудности или были ошибки.
Поставьте себе оценки за домашнее задание.
35.
Урок окончен!УДАЧИ ВАМ!


































 mathematics
mathematics








