Similar presentations:
Сложение и умножение числовых неравенств. Теоремы о почленном сложении и умножении неравенств
1. «Сложение и умножение числовых неравенств»
2. Цель урока:
1. Рассмотреть теоремы о почленномсложении и умножении неравенств
2. Научиться применять их при оценке
выражений
3.Закрепить свойства неравенств
3. План урока:
1. Устная работа2. Объяснение нового материала
3. Закрепление изученного
материала
4. Итоги урока
5. Задание на дом
4. Устная работа:
1) Сформулируйте теоремы,выражающие основные
свойства числовых
неравенств.
Приведите свои примеры.
5. Теорема 1:
Если a<b и b<c,то a<c
6. Теорема 2:
Если a<b и c – любое число,то a+c<b+c
Если к обеим частям верного
неравенства прибавить
одно и то же число, то
получится верное неравенство
7. Теорема 3(1):
Если a < b и c – положительноечисло, то ac<bc.
a < b x c >0
ac < bc
Если обе части верного неравенства
умножить или разделить на одно и то
же положительное число, то
получится верное неравенство
8. Теорема 3(2)
Если a<b и c – отрицательноечисло, то ac>bc
a<b xc<0
ac > bc
Если обе части верного неравенства
умножить или разделить на одно и то же
отрицательное число и изменить знак
неравенства на противоположный, то
получится верное неравенство.
9. Следствие из теорем
Если a и b – положительныечисла и a<b, то 1/a > 1/b
10.
2) Дано: a>bСравните: а) 2а и 2b;
б) -23а и -23b;
11. 3) Дано: 7 < x < 11
3) Дано: 7 < x < 11Оцените значение выражения:
А) 4х;
Б) -3х;
В) -х;
Г) 1/x.
12. Объяснение нового материала «Сложение и умножение числовых неравенств»
13.
Теорема 1Если сложить почленно верные числовые
неравенства одного знака, то получится
верное неравенство.
a>b
+ c>d
a+c > b+d
#1
+
-7<15
7<12
0<27 – верно
#2
-10>-13
+
7> 2
-3>-11 - верно
14.
Теорема 2Если перемножить почленно верные
неравенства одного знака, левые и
a>b
,
где
a>0,
b>0
правые части которых – положительные
+ числа, то получится верное
c>d , где c>0, d>0
неравенство.
ac >bd
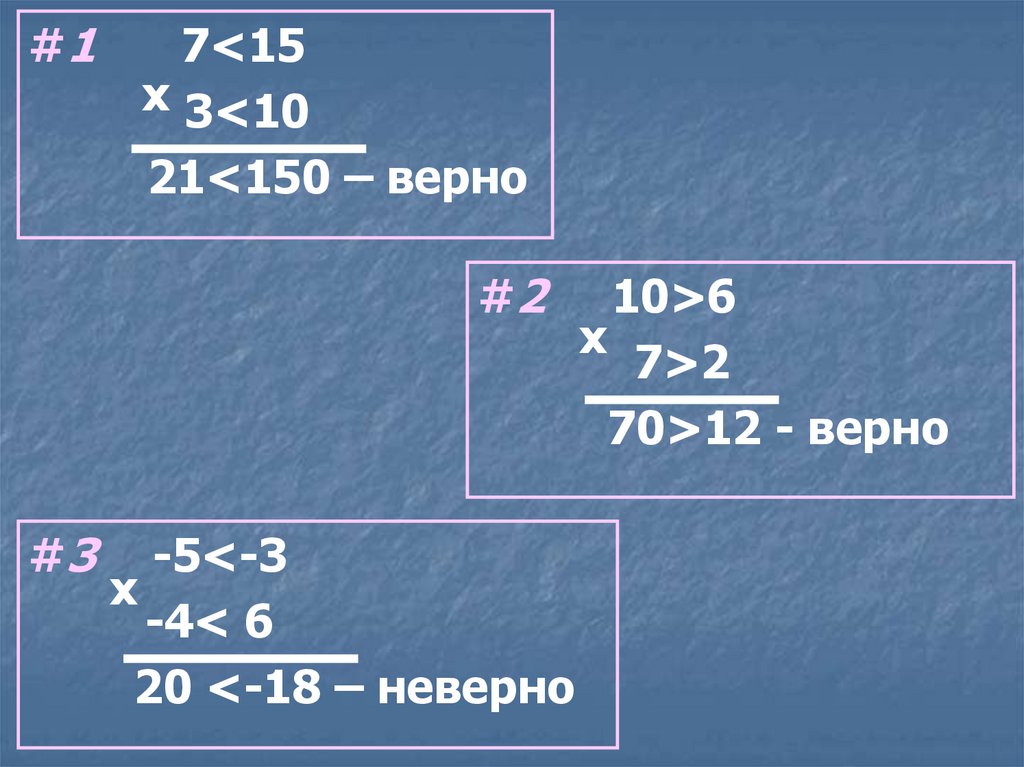
15.
#17<15
х 3<10
21<150 – верно
#2
#3
-5<-3
х
-4< 6
20 <-18 – неверно
10>6
х
7>2
70>12 - верно
16.
a<bСледствие:
n
Если числа a и bn- положительные
и
a
<
b
n
n
a<b, то a <b (n – натуральное число)
#
3>2
3 >2
2
2
9>4 - верно
17. 3. Закрепление изученного материала
Решить задания: № 765;766;
768;
770;
772
Дополнительно: № 774
18. 4. Итог урока
1. Сформулируйте теорему о почленномсложении неравенств
2. Сформулируйте теорему о почленном
умножении неравенств
19. 5. Задание на дом
П. 30( правила);№769;773;780;
781(а)



















 mathematics
mathematics








