Уравнения и неравенства (лекция 4)

1.

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«МИРЭА – Российский технологический университет»
РТУ МИРЭА
Колледж программирования и кибербезопасности
УЧЕБНАЯ ДИСЦИПЛИНА/ МЕЖДИСЦИПЛИНАРНЫЙ КУРС
ОУД.07 Математика (включая алгебру, начала математического
анализа и геометрию))_______________________________________
(код.полное название дисциплины, без сокращений)
ПЦК Общеобразовательных дисциплин_______________________
(полное наименование ПЦК)
ВИД УЧЕБНОГО
МАТЕРИАЛА лекционные материалы________________________
(в соответствии с п.п. 1-11)
ПРЕПОДАВАТЕЛЬ Добрынина Надежда Владимировна________
(фамилия, имя, отчество)
СЕМЕСТР 1 семестр 2024-2025 уч. Года________________________
(указать семестр обучения, учебный год)

2.

Уравнения и неравенства.
Лекция

3.

Что такое уравнение?
Что значит решить уравнение?

4.

Рациональные уравнения

5.

Что такое рациональное уравнение?

6.

Рациональные уравнения – это
уравнения, в которых и левая, и
правая части рациональные
выражения.

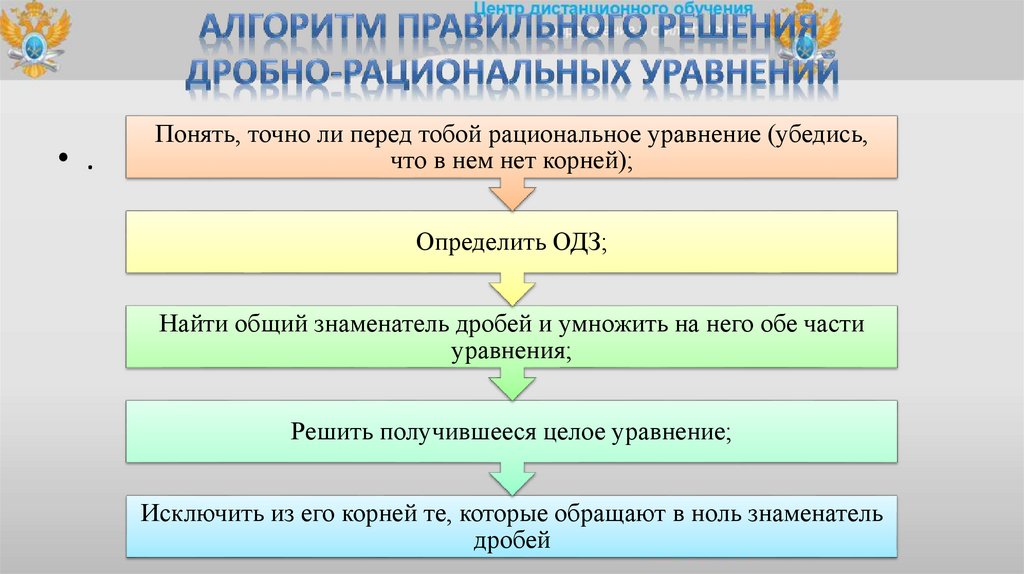
7.

• .
Понять, точно ли перед тобой рациональное уравнение (убедись,
что в нем нет корней);
Определить ОДЗ;
Найти общий знаменатель дробей и умножить на него обе части
уравнения;
Решить получившееся целое уравнение;
Исключить из его корней те, которые обращают в ноль знаменатель
дробей

8.

Примерa: Решите уравнение:
Решение.
1
Ответ: х=−3 3.

9.

Метод замены переменных

10.

Пример . Решить уравнение:
Решение. Введем замену:
тогда наше уравнение примет вид:
Введем обратную замену:
Корнями первого уравнения является пара чисел х=±2. Второе не имеет
корней.
Ответ: х=±2.

11.

1. Решите уравнение:
2. Решите уравнение:
3. Решите уравнение:
4. Решите уравнение:

12.

Ответы:
• 1) -1; -4
• 2) 2,8
• 3) -3 и 3
• 4) -0,5 и 0

13.

https://www.yaklass.ru/p/algebra/8klass/kvadratnye-uravneniia11021/ratcionalnye-uravneniia9118/re-1d0e092f-b0c0-44ee-81b47255e1d7cbfe

14.

Графический метод решения
уравнений и неравенств.

15.

Алгоритм решения уравнений графическим
способом.
1. Составить функции по левой и правой части
уравнения.
2. Составить таблицу значений каждой функции.
3. В одной системе координат построить графики этих
функций .
4. Найти точки пересечения 2-х графиков.
5. Опустить из найденных точек на ось абсцисс
перпендикуляры и найти значения (х).
6. Абсциссы точек пересечения – это корни уравнения.
Записать их в ответ, используя знак приближённого
равенства.

16.

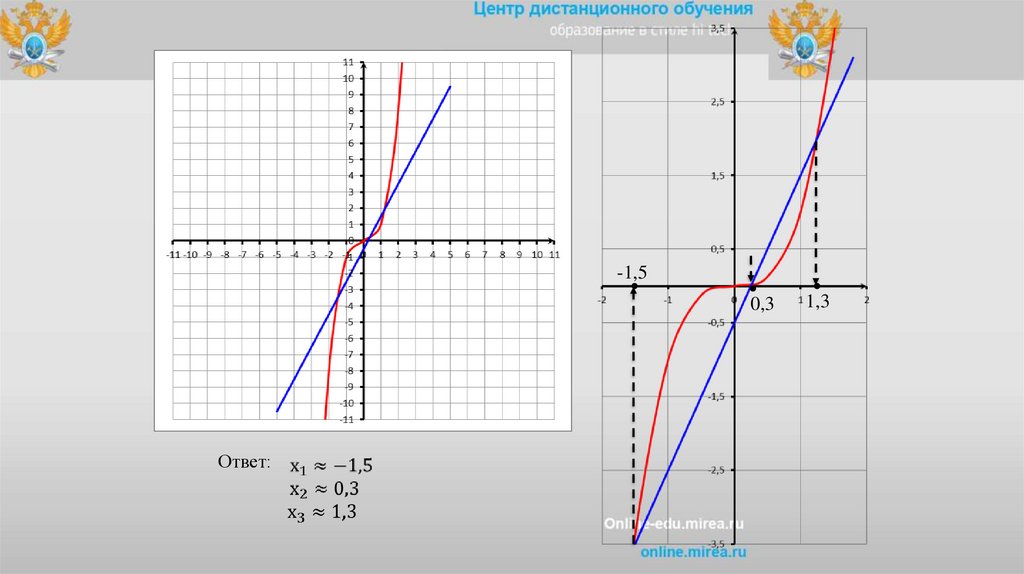
Решить уравнение
x 3 2 x 0,5 0
x 3 2 x 0,5
представим
построим в одной системе координат
y x3
x
y
-3 -2
-27 -8
-1
-1
0
0
y 2 x 0,5
1
1
2
8
3
27
x
y
0
1
-0,5 1,5

17.

-1,5
0,3
Ответ:
1,3

18.

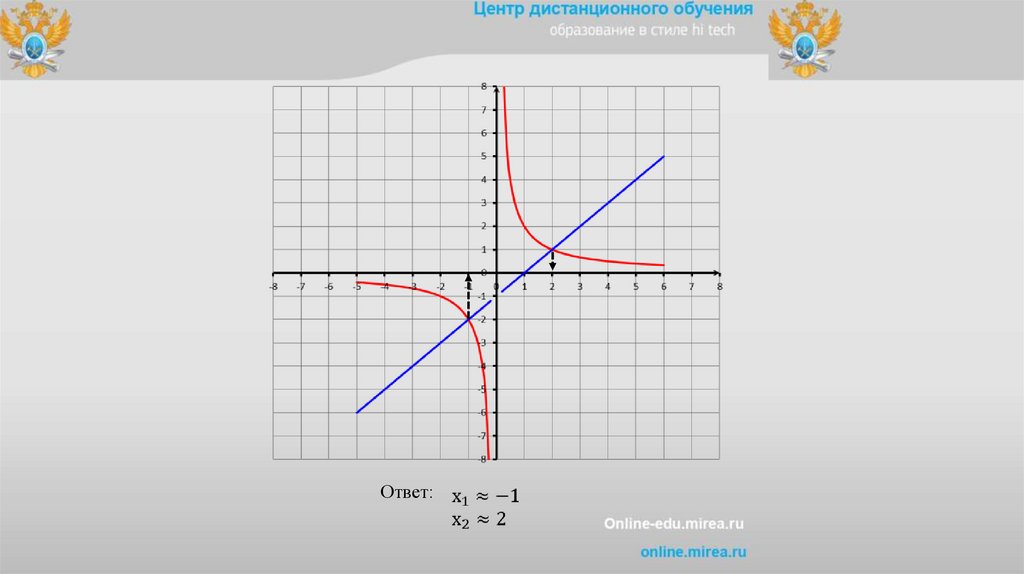
Решить 2уравнение
x 1 0
х
2
x 1
х
представим
построим в одной системе координат
2
y
х
y x 1
x
-4
-2
-1
1
2
4
x
0
1
y
-0,5 -1
-2
2
1
0,5
y
-1
0

19.

Ответ:

20.

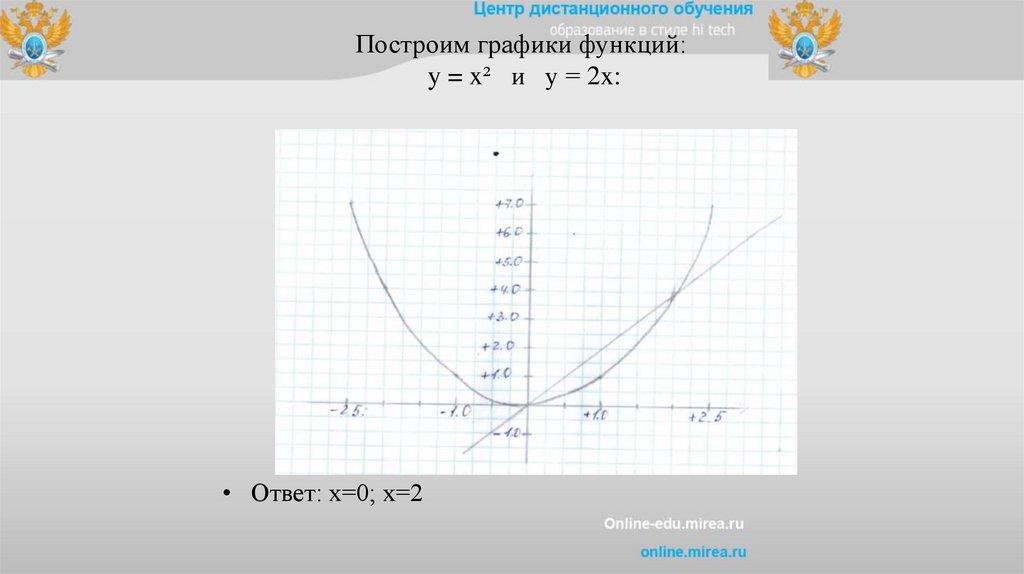
Задание:
Решить уравнение: x² - 2x=0
Решение:
Перепишем уравнение в виде:
x² = 2x

21.

Построим графики функций:
y = x² и y = 2x:
• Ответ: х=0; х=2

22.

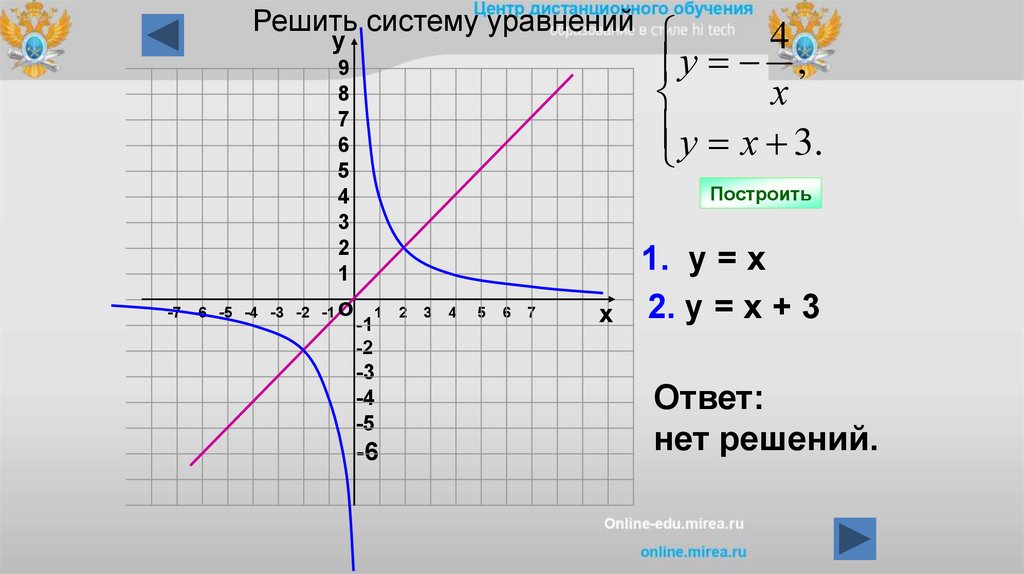
Решить систему уравнений
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
4
у ,
х
у х 3.
Построить
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
1. у = х
2. у = х + 3
Ответ:
нет решений.

23.

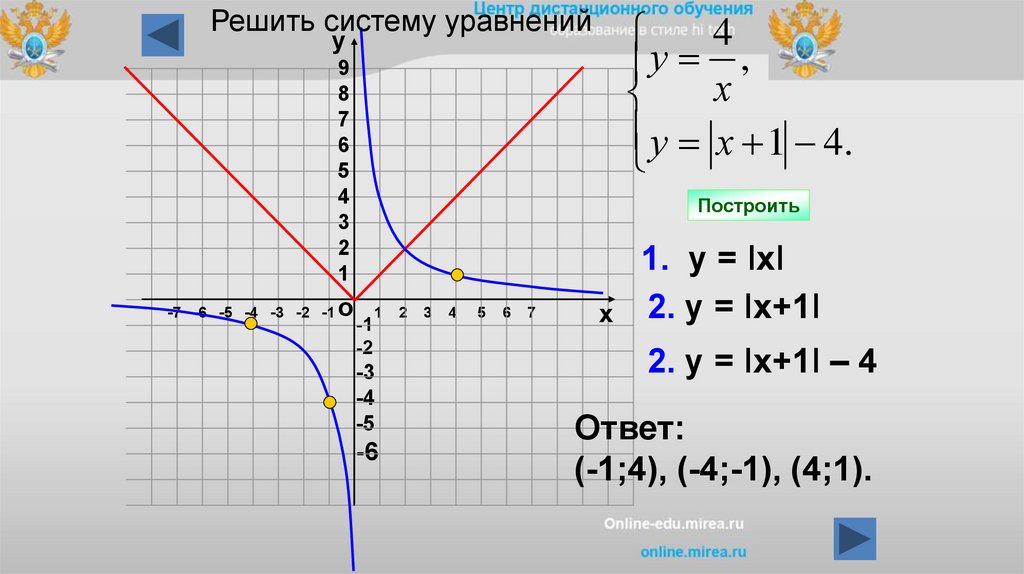
Решить систему уравнений
4
у ,
х
у х 1 4.
у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
Построить
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
1. у = IхI
2. у = Iх+1I
2. у = Iх+1I – 4
Ответ:
(-1;4), (-4;-1), (4;1).

24.

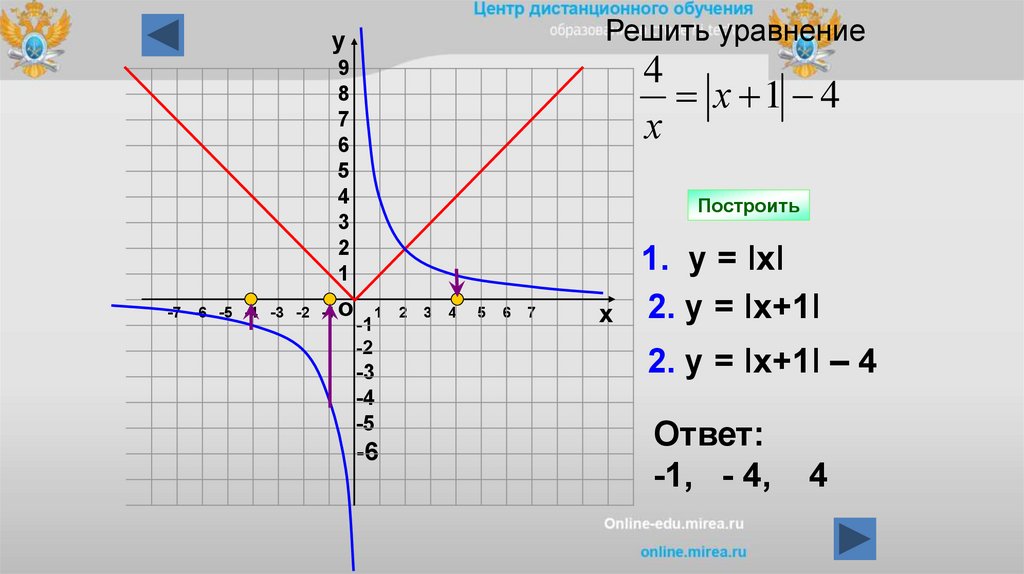
Решить уравнение
у
4
х 1 4
х
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2 -1
о
Построить
-1
-2
1
-3
-4
-5
-6
2
3
4
5
6
7
х
1. у = IхI
2. у = Iх+1I
2. у = Iх+1I – 4
Ответ:
-1, - 4,
4

25.

26.

у
Используя график функции
а) охарактеризуйте знак
первого коэффициента а и
дискриминанта;
б) назовите значения
переменной х , при которых
функция принимает значения,
- равные нулю,
- положительные значения,
- отрицательные значения.
-2
о 2
х

27.

Алгоритм решения неравенств вида ax2+bx+c>0 и
ax2+bx+c<0
методом интервалов
1. Найти корни уравнения ах2+bx+c=0
2. На ось ОХ нанести корни уравнения.
(Они разбивают ось на интервалы).
Расставить знаки на интервалах.
3. Найти значения переменной х, удовлетворяющие
данному неравенству. Записать их в виде неравенства.
4. Записать ответ.

28.

№1. Найдите множество решений неравенства:
1. Найдем корни уравнения:2 х 2 3 х 5 0
2. На ось ОХ нанесем корни и расставим знаки
+
\\\\\\\\\\\\\\
-
+
/////////////////
х
-2,5
1
3. Найдем значения х, удовлетворяющие неравенству
х ≤ -2,5; х ≥ 1
4.

29.

№ 2. Решите неравенство:
в ) 4 х 12 х 9 0
2
2 х 3 0
2
х 1,5
x < 1,5 ; x > 1,5
+
+
\\\\\\\\\\\\\\\ //////////////////////////
1,5
х

30.

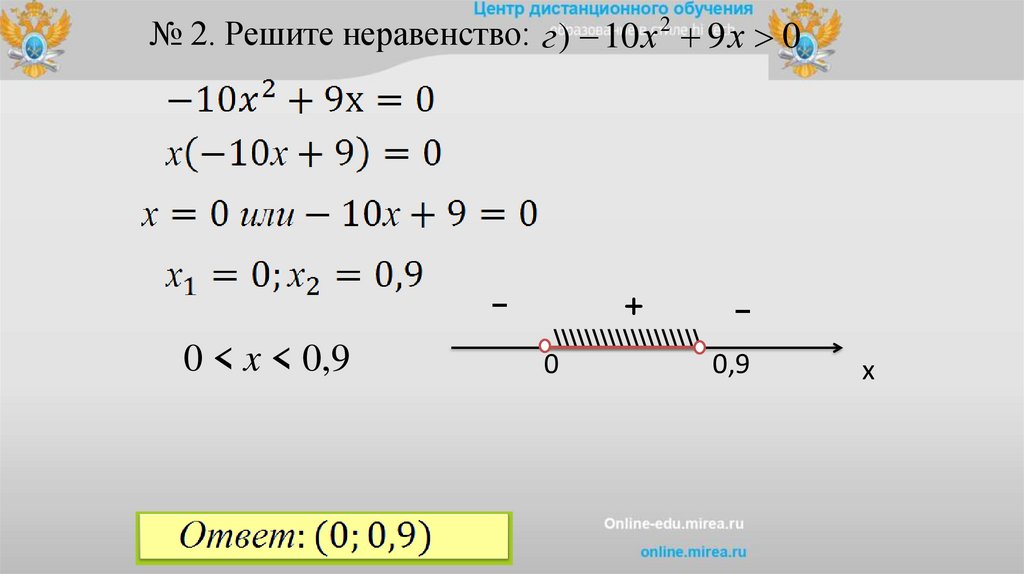
№ 2. Решите неравенство: г ) 10 х 2 9 х 0
-
0 < x < 0,9
+
\\\\\\\\\\\\\\\\\\\
0
0,9
х

31.

№3. Решите неравенство:
а) x2 < 49
x2 – 49 < 0
x2 – 49 = 0
х 49
х1 7, х2 7
2
–7<x<7
+
//////////////////
-7
Ответ : 7;7
+
7
х

32.

№4. Решите неравенство:
а ) х 16 х 0
3
x x 16 0
x x 4 x 4 0
2
-
//////////////
-4
+
+
-
//////////////
0
x x 4 x 4 0
x 0; x 4 0; x 4 0
x 4
x 4
4
x 4; 0 x 4
Ответ : ; 4 0;4

33.

План применения метода интервалов
!
• Разложить многочлен на простые
множители;
• найти корни многочлена;
• изобразить их на числовой прямой;
• разбить числовую прямую на интервалы;
• определить знаки множителей на
интервалах знакопостоянства;
• выбрать промежутки нужного знака;
• записать ответ (с помощью скобок или
знаков неравенства).

34.

Решить неравенство
х 2 х 5 х 4 0
х1 2, х2 5, х3 4
нули функции
f ( x) х 2 х 5 х 4 .
-
+?
-6
-5
+
0
2
3
4
5
(3)
305 54;
44 6 30
40
((0)
(5)
6)
56 30
5
48 80
035 622 2
хfff
5;

35.

Самостоятельная работа
Вариант 1.
Вариант 2.
№1. Решите методом интервалов неравенства:
а) (2 x 5)( x 3) 0;
а) (5 x 2)( x 4) 0;
б) 4 x 2 4 x 3 0.
б) 9 x 2 3x 2 0.
№2. Найдите область определения функции:
y 6 x x 2 3 3 2 x 5.
!
y 2 7 x x 2 5 5 3x 4.

36.

Проверь своё решение
Вариант 1.
Вариант 2.
№1. Решите методом интервалов неравенства:
а) (2 x 5)( x 3) 0
а) (5 x 2)( x 4) 0
2 x 2,5 x 3 0 2
5 x 0, 4 x 4 0 5
x 2,5 x 3 0
x 0, 4 x 4 0
–
+
-3
Ответ:
+
2,5
–
+
x
; 3 2,5; .
-4
Ответ:
+
0,4
4;0,4
x

37.

Проверь своё решение
Вариант 1.
Вариант 2.
№1. Решите методом интервалов неравенства:
б) 4 x 2 4 x 3 0
б)
3
1
4 x x 0 4
2
2
3
1
x x 0
2
2
–
+
-3/2
+
1/2
3 1
Ответ: ;
2 2
9 x 2 3x 2 0.
2
1
9 x x 0 9
3
3
2
1
x x 0
3
3
–
+
x
-2/3
+
1/3
2
Ответ: ;
3
x
1
;
.
3

38.

Проверь своё решение
Вариант 1.
Вариант 2.
№2. Найдите область определения функции:
y 6x x2 3 3 2x 5
y 2 7 x x 2 5 5 3x 4
Решение.
Решение.
6 x x 0 1
7 x x 0 1
x2 6 x 0
x( x 6) 0
x 7x 0
x( x 7) 0
2
2
–
+
0
Ответ:
+
6
0; 6
2
–
+
x
0
Ответ:
0; 7
+
7
x

39.

Оценка самостоятельной работы
!
За каждый верно выполненный
пример – поставьте 1 балл.
0 баллов – плохо, «2».
1 балл – удовлетворительно, «3».
2 балла – хорошо, «4».
3 балла – отлично, «5».

40.

Решение рациональных неравенств
P x
0.
Q x
Умножим обе части такого неравенства на многочлен Q x .
2
Знак исходного неравенства не меняется, (т.к Q x 0 ).
2
Получаем неравенство P( x) Q( x) 0 , равносильное
данному неравенству, которое решаем методом интервалов.
Итак:
Решение рациональных неравенств
равносильно решению системы:
!
P( x) Q( x) 0,
P( x)
0
Q( x)
Q( x) 0.

41.

x 7 x 2 0 1
x 7 x 2 0
2
7

42.

4
x 8,5 x 4 0
x 4
8,5
2 x 8,5 x 4 0 2
x 8,5 x 4 0

43.

Самостоятельная работа
Решите неравенства:
Уровень А
1. x 3 0
x 6
2. 3 x 0
x 4
3.
x 6,8
0
7 x x 4
Уровень В
2
1. x 5 x
x 16 0
2
2
x
6x 7
2.
0
2
x 25
3. Найдите область
определения функции
16 24 x 9 x 2
y
x 2

44.

Самостоятельная работа
Решите неравенства:
Уровень А
Уровень В
1. (-3;6)
1. (-∞;-5] [-4;0] [4;+∞)
2. (-∞;-7] (-5;1] (5;+∞)
2. [3;4)
3.
3. [-6,8;4) (7;+∞)

45.

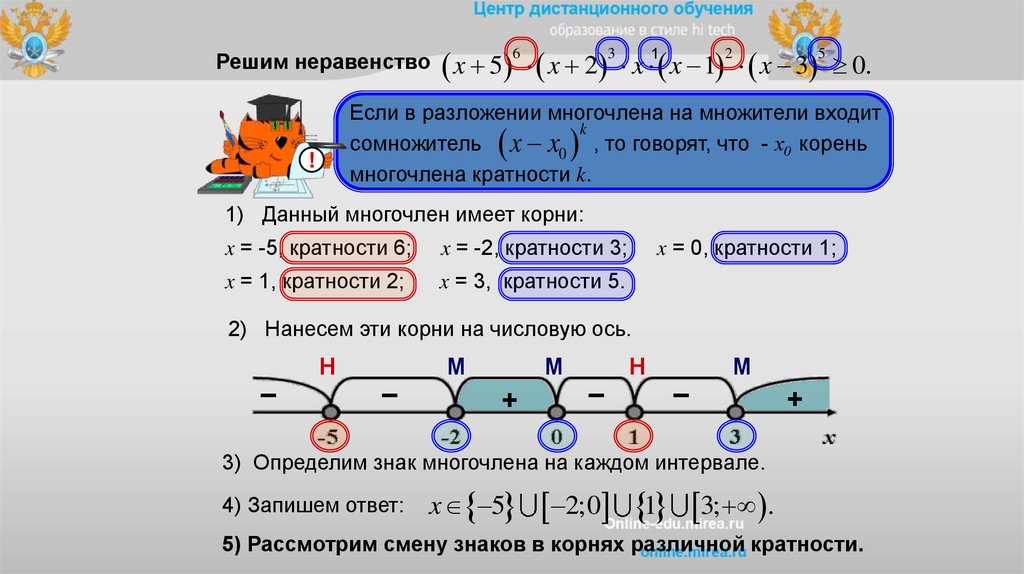
Решим неравенство x 5 x 2 x 1 x 1 x 3 0.
6
3
2
5
Если в разложении многочлена на множители входит
k
сомножитель x x0 , то говорят, что - х0 корень
многочлена кратности k.
!
1) Данный многочлен имеет корни:
x = -5, кратности 6;
x = -2, кратности 3;
x = 1, кратности 2;
x = 3, кратности 5.
x = 0, кратности 1;
2) Нанесем эти корни на числовую ось.
–
Н
–
М
М
+
–
Н
–
М
+
3) Определим знак многочлена на каждом интервале.
4) Запишем ответ:
x 5
2;0 1 3; .
5) Рассмотрим смену знаков в корнях различной кратности.

46.

Обобщая ваши наблюдения, делаем выводы:
1
Для решения неравенства важно знать,
является ли k четным или нечетным числом.
2
При четном k многочлен справа и слева от х0
имеет один и тот же знак
(знак многочлена не меняется).
3
При нечетном k многочлен справа и слева от
х0 имеет противоположные знаки
(знак многочлена изменяется).

47.

Спасибо за внимание!