Similar presentations:
Векторы. Произведения векторов (лекция 3)
1.
МеждународнаяДисциплина
образовательная
«Математика 1»
корпорация
Векторы.
Произведения
векторов
Лекция 3
Буганова Светлана Николаевна
2023-2024 учебный год
2.
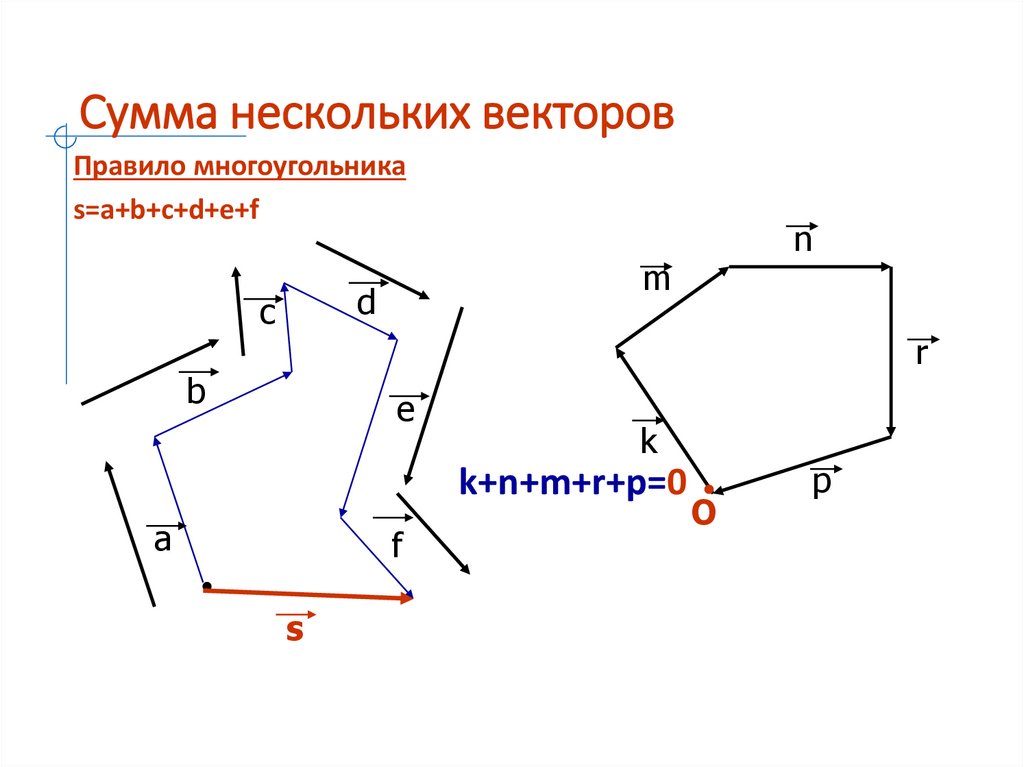
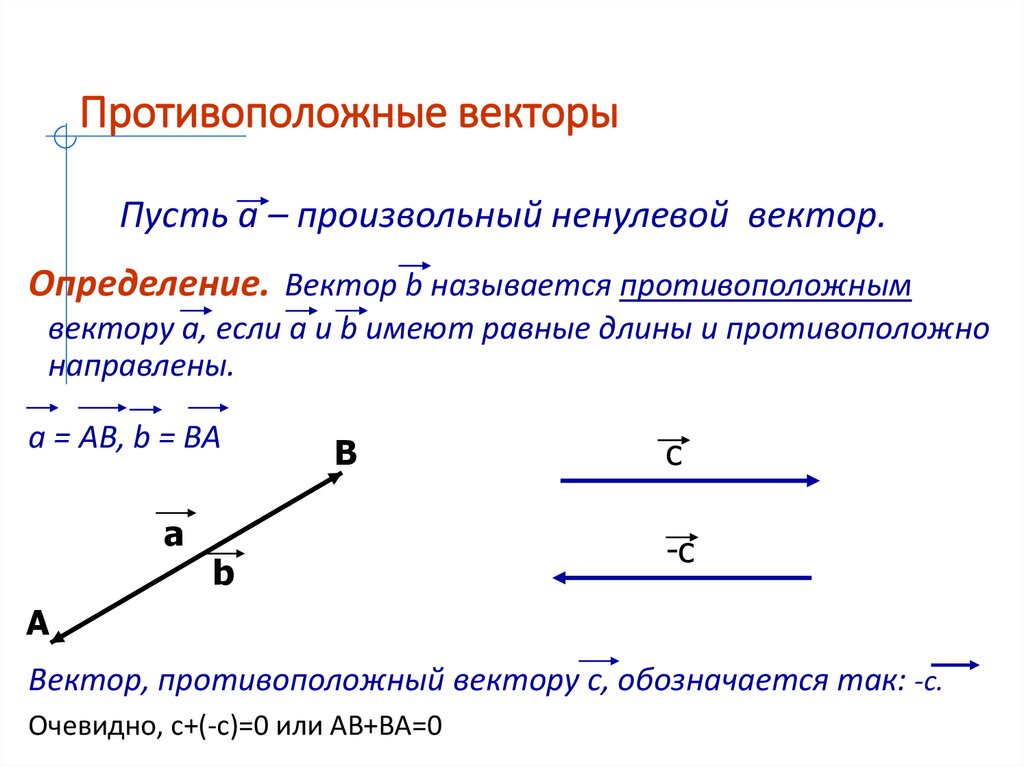
План лекции1. Понятие вектора.
2. Действия над векторами.
3. Скалярное произведение
векторов.
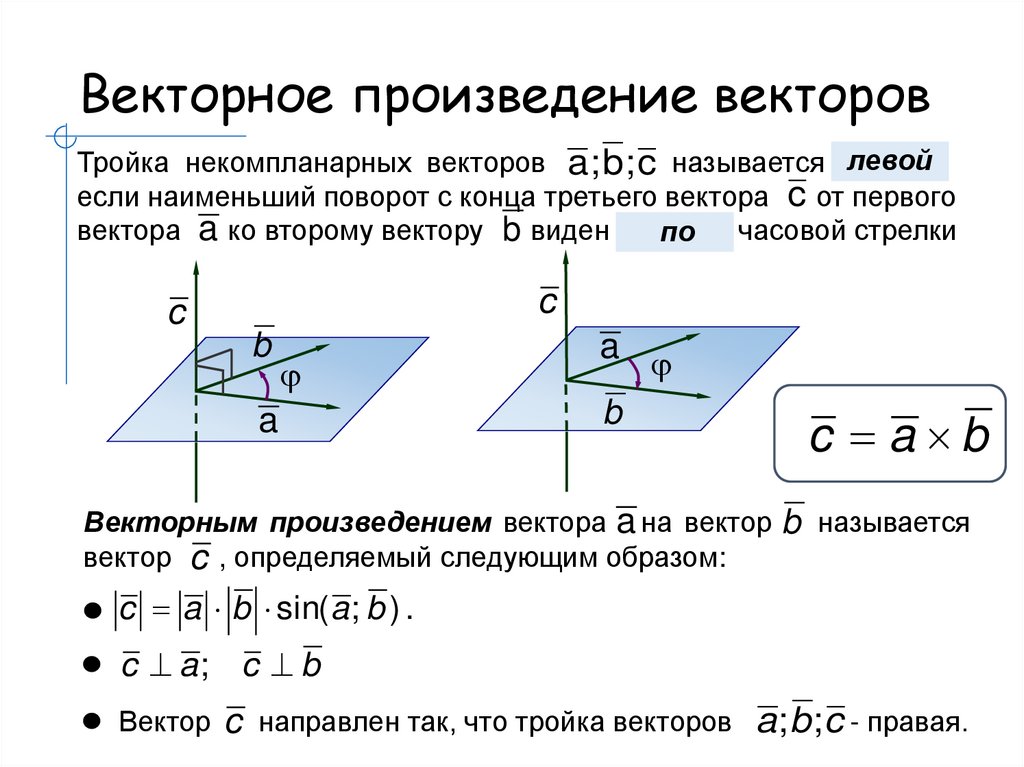
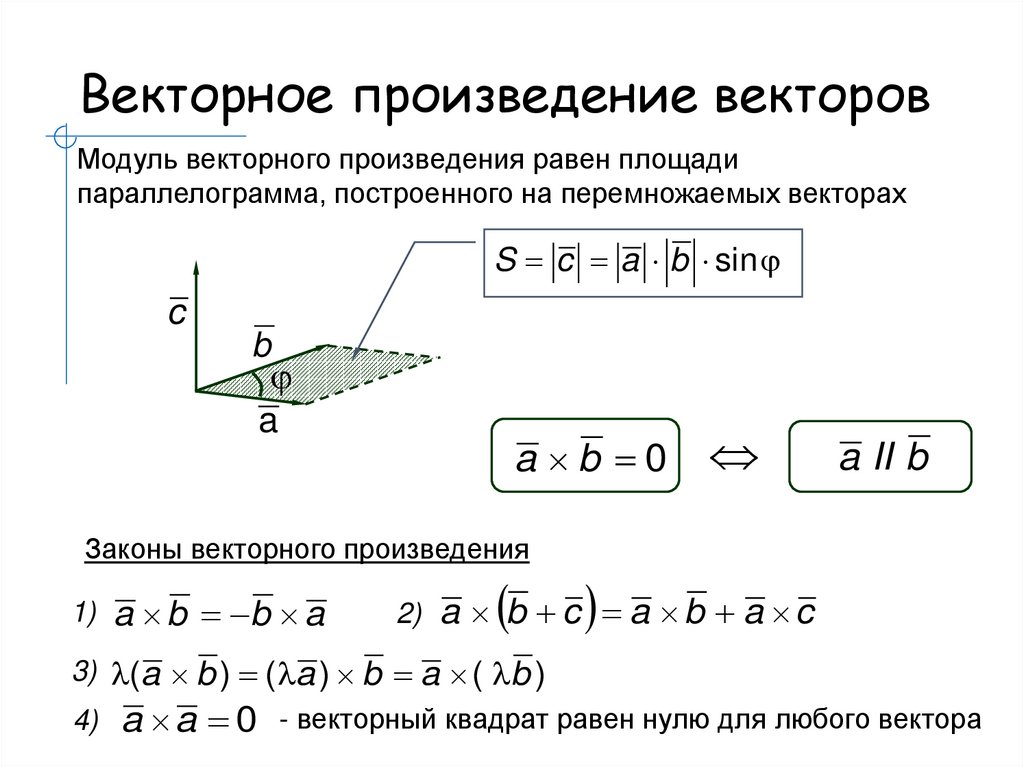
4. Векторное произведение
векторов.
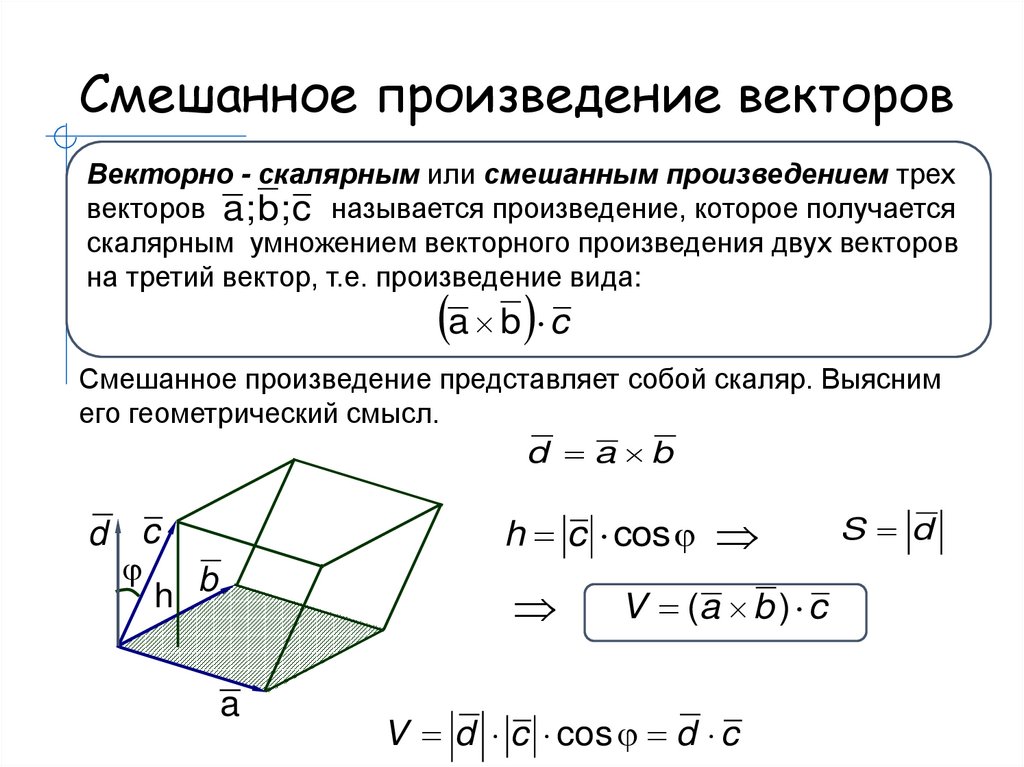
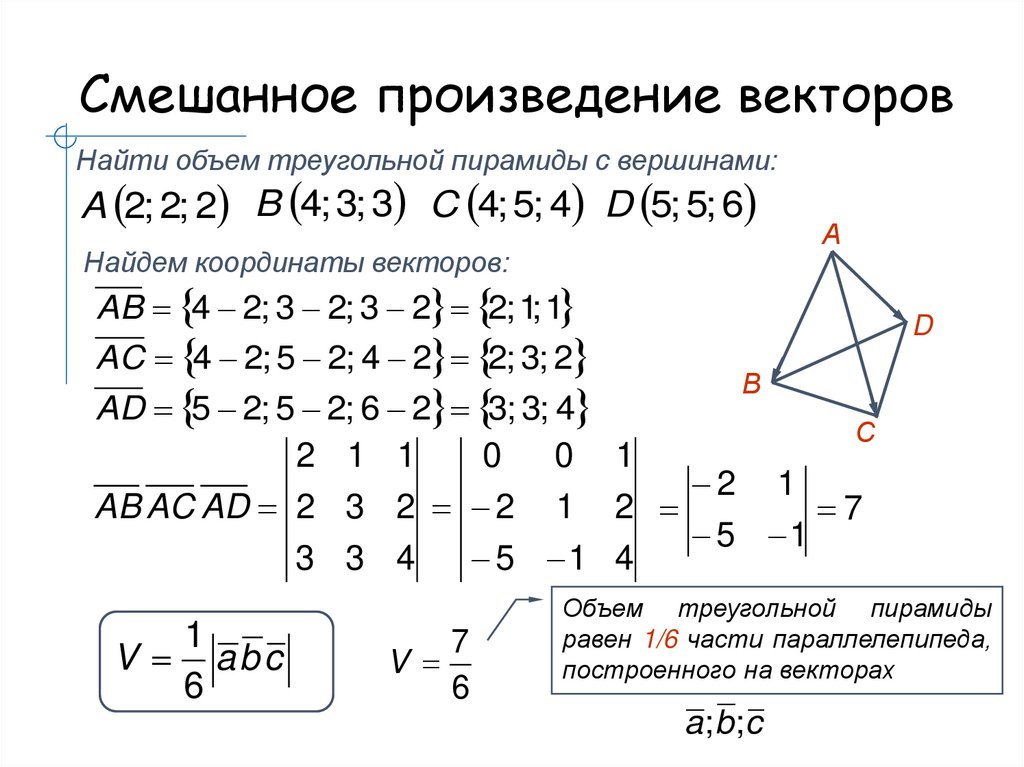
5. Смешанное произведение
векторов.
2
3.
Понятие вектора• Рассмотрим произвольный отрезок.
На нем можно указать два
направления.
Чтобы выбрать одно из
направлений, один конец отрезка
назовем НАЧАЛОМ, а другой –
КОНЦОМ и будем считать, что
отрезок направлен от начала к концу.
•Определение.
Отрезок, для
которого указано,
какой из его концов
считается началом, а
какой - концом,
называется
направленным
отрезком или
вектором.
4.
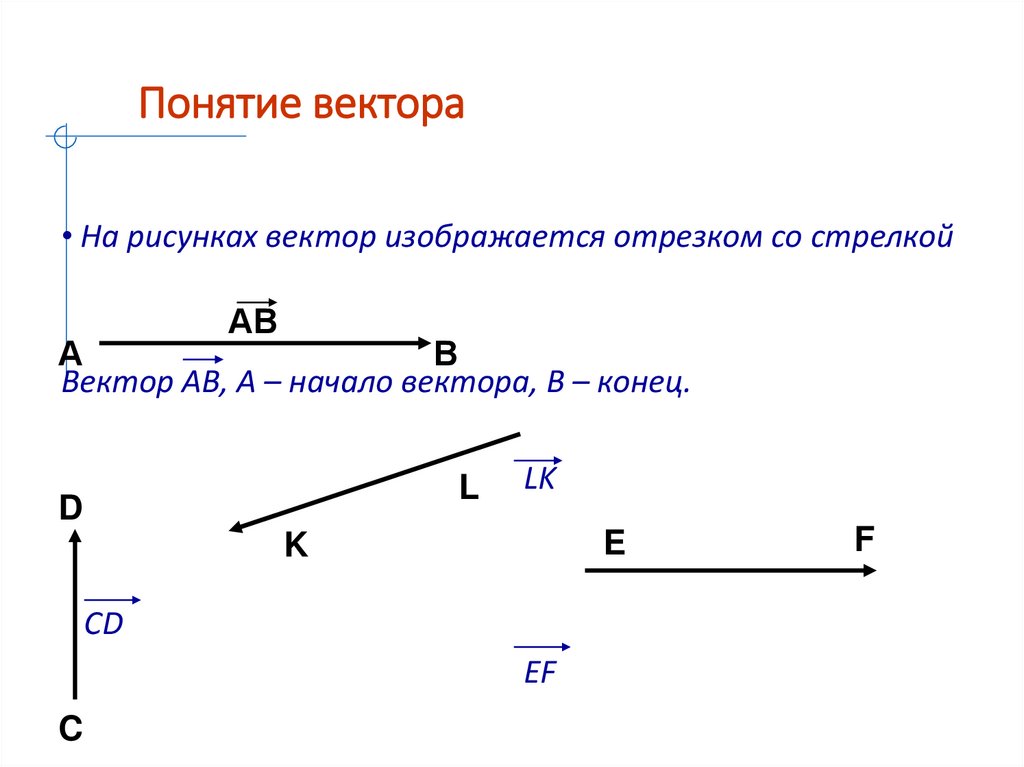
Понятие вектора• На рисунках вектор изображается отрезком со стрелкой
АВ
А
В
Вектор АВ, А – начало вектора, В – конец.
L
D
LK
E
K
CD
EF
C
F
5.
Понятие вектора• Векторы часто обозначают и одной строчной латинской
буквой со стрелкой над ней:
b
a
c
• Любая точка плоскости также является вектором, который
называется НУЛЕВЫМ. Начало нулевого вектора совпадает с его
концом:
ММ = 0.
М
6.
Понятие вектора• Длиной или модулем ненулевого вектора АВ
называется длина отрезка АВ:
с
АВ = а = 5
В
a
с = 17
А
• Длина нулевого вектора считается равной нулю:
ММ = 0.
М
7.
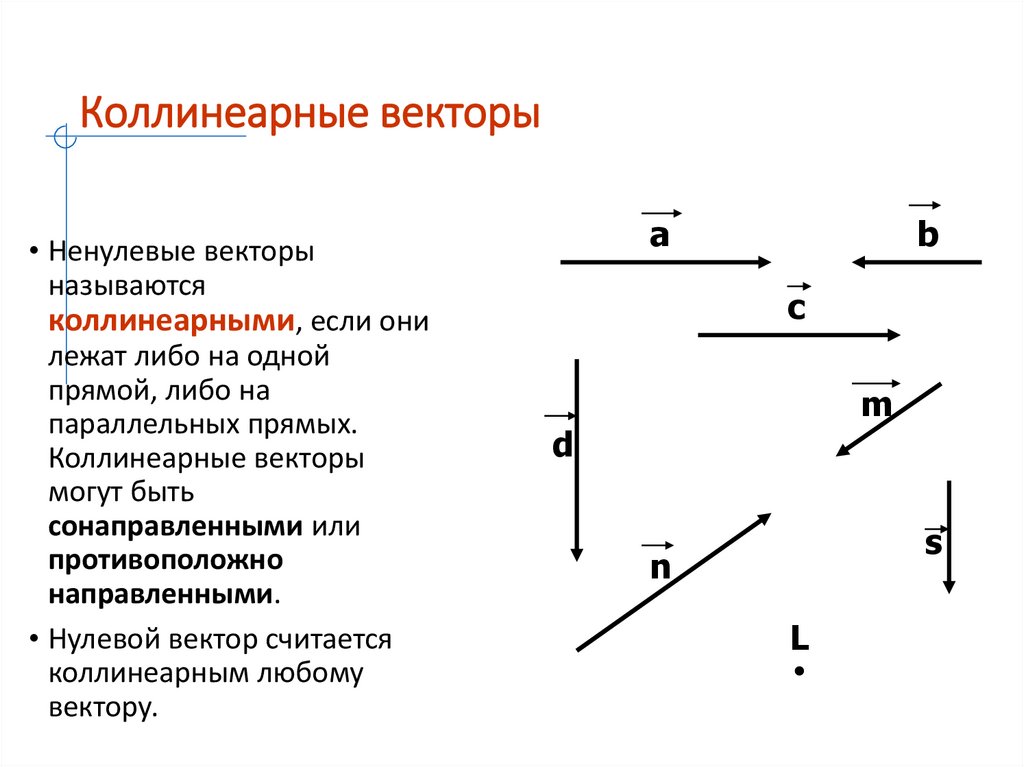
Коллинеарные векторы• Ненулевые векторы
называются
коллинеарными, если они
лежат либо на одной
прямой, либо на
параллельных прямых.
Коллинеарные векторы
могут быть
сонаправленными или
противоположно
направленными.
• Нулевой вектор считается
коллинеарным любому
вектору.
а
b
c
m
d
s
n
L
8.
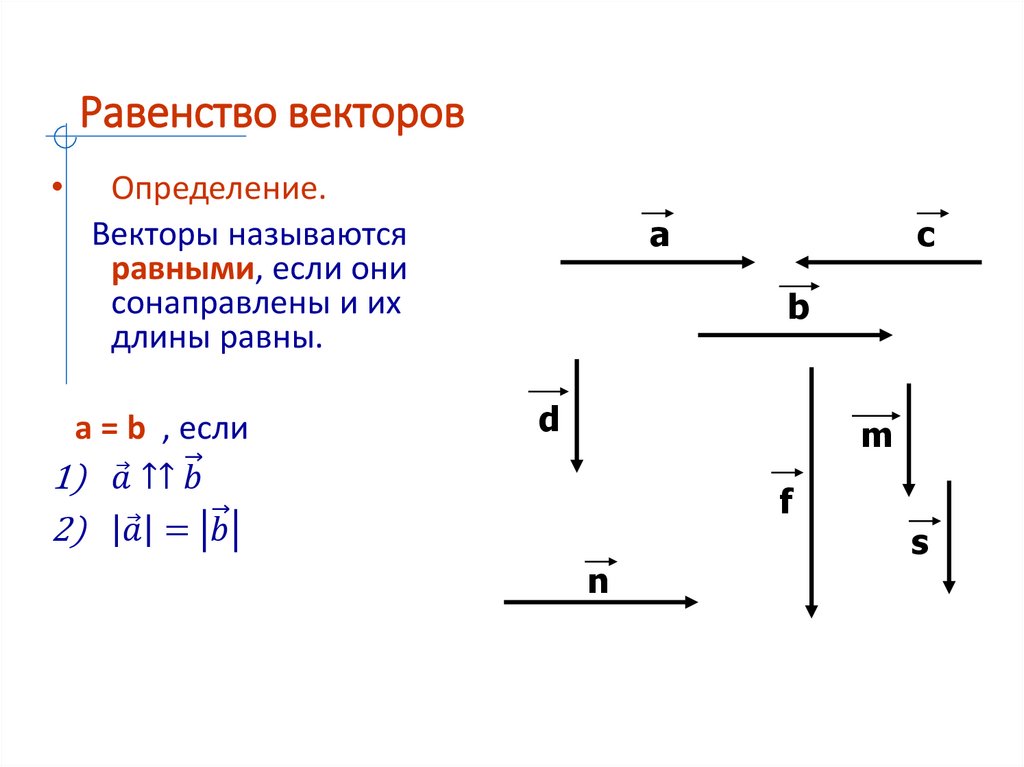
Равенство векторовОпределение.
Векторы называются
равными, если они
сонаправлены и их
длины равны.
а = b , если
1)





















 mathematics
mathematics








