Similar presentations:
Системи рівнянь
1.
2.
формувати вміння розв’язувати системи лінійних рівнянь здвома змінними ;
розвивати навички, увагу, уміння порівнювати, аналізувати,
робити висновки;
виховувати відповідальність, самостійність, любов до
навчання та вміння працювати разом, намагатися скласти
ситуацію успіху для кожного учня.
3.
4.
Виразимо учерез х
Розв'язування системи
10 графічним способом
y
y=x-1
6
Побудуємо графік
першого рівняння
х 0 1
у = х-1
у -1 0
А(2;1)
2
Побудуємо графік
другого рівняння
х 2
у1
1
х+2у=4
0
2
-2
0
1
4
Відповідь: (2; 1)
10
x
5.
Графічний спосіб (алгоритм)• Виразити у через х в кожному рівнянні
• Побудувати в одній системі координат
графік кожного рівняння
• Визначити координати точки перетину
• Записати відповідь: х=…; у=… , або
• (х; у).
6.
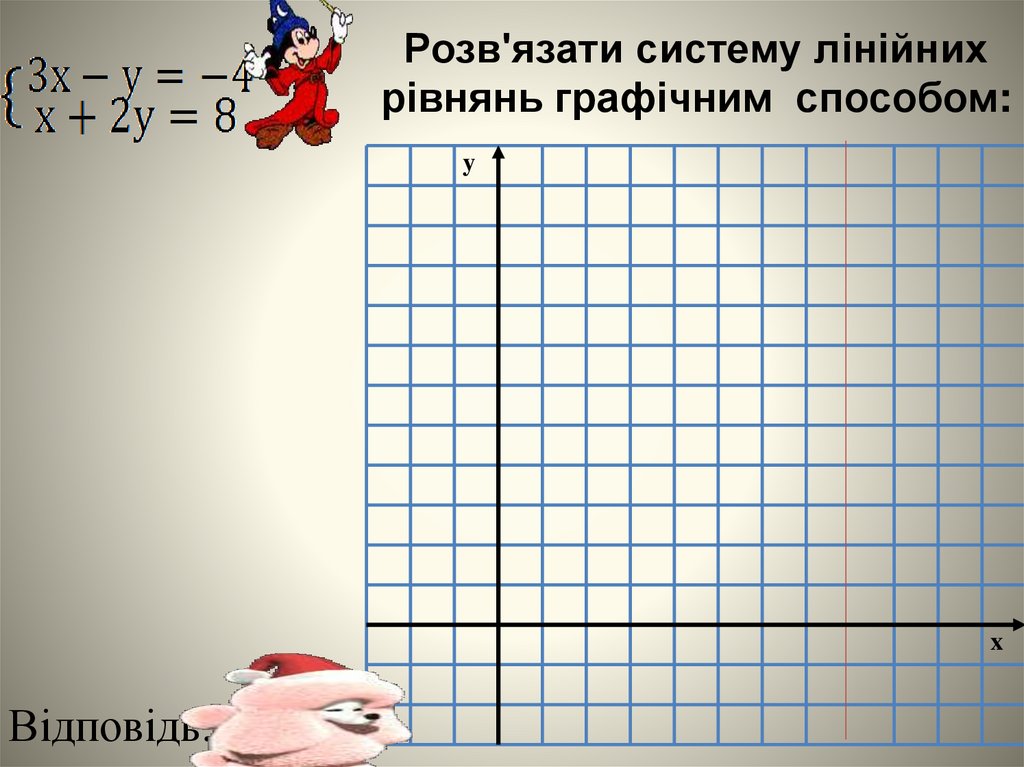
Розв'язати систему лінійнихрівнянь графічним способом:
y
x
Відповідь:
7.
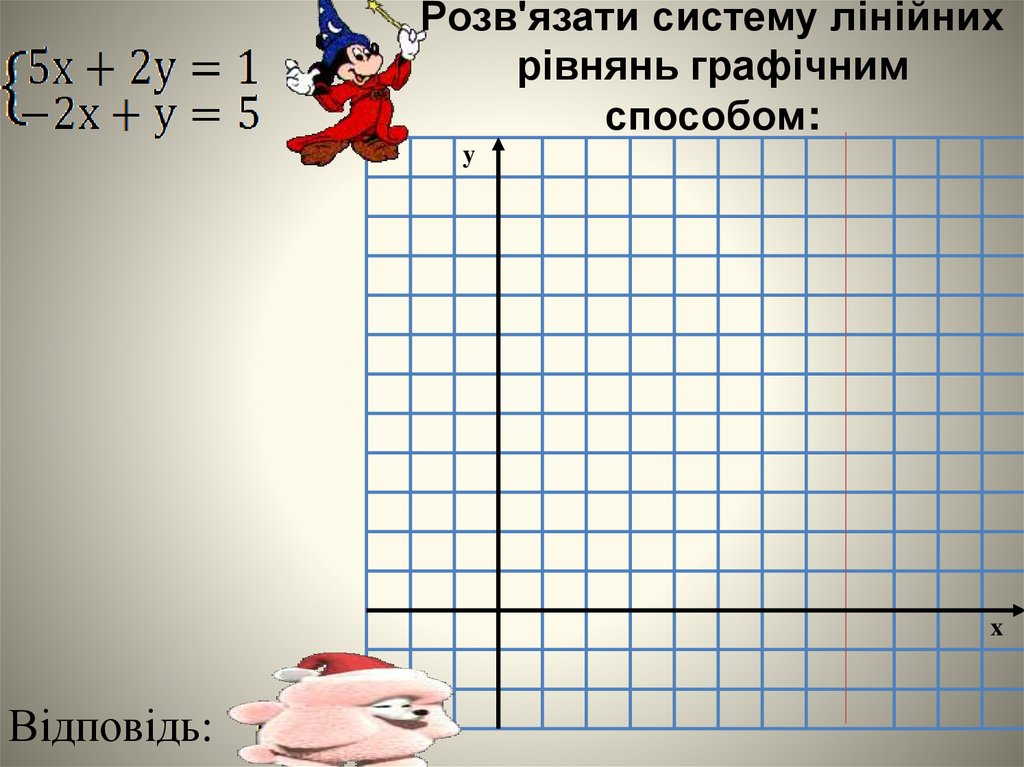
Розв'язати систему лінійнихрівнянь графічним
способом:
y
x
Відповідь:
8.
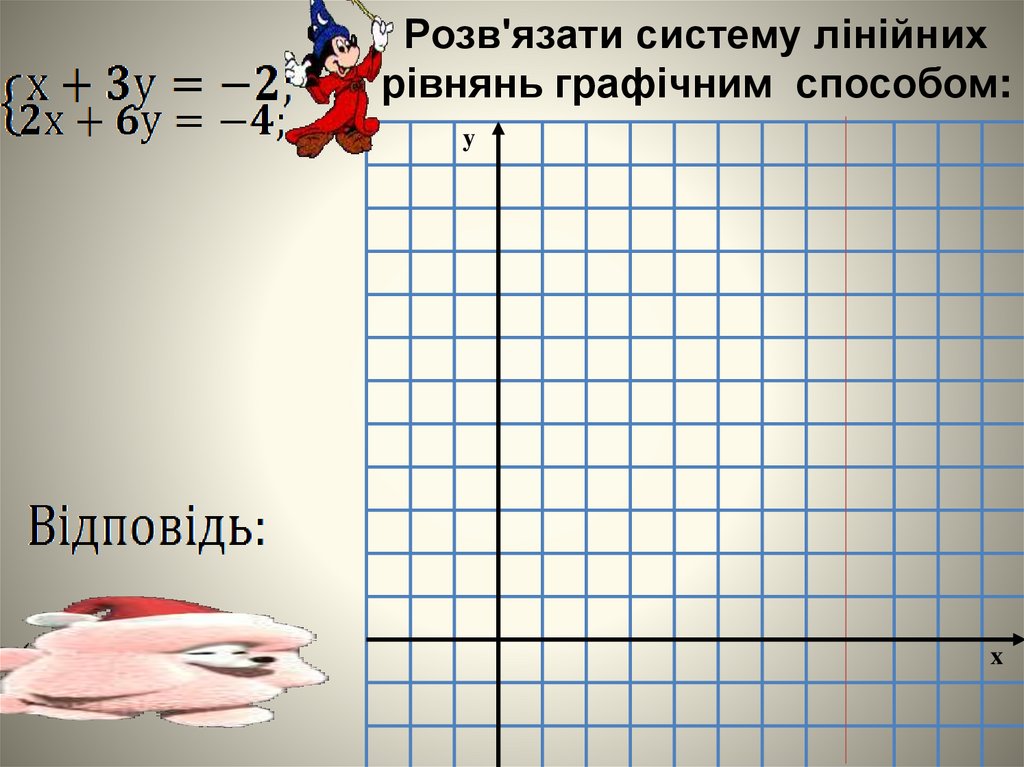
Розв'язати систему лінійнихрівнянь графічним способом:
y
x
9.
Розв'язати систему лінійнихрівнянь графічним способом:
y
x
10.
Розв'язати систему лінійнихрівнянь графічним
способом:
y
x
11.
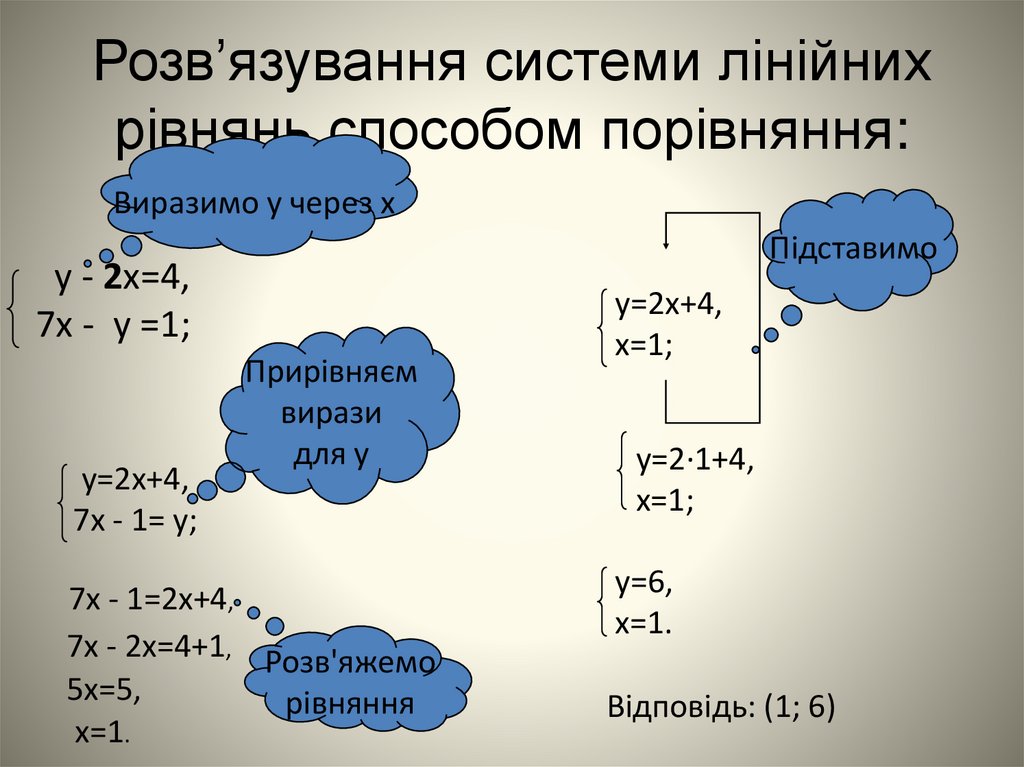
Розв’язування системи лінійнихрівнянь способом порівняння:
Виразимо у через х
Підставимо
у - 2х=4,
7х - у =1;
у=2х+4,
7х - 1= у;
Прирівняєм
вирази
для у
7х - 1=2х+4,
7х - 2х=4+1, Розв'яжемо
5х=5,
рівняння
х=1.
у=2х+4,
х=1;
у=2·1+4,
х=1;
у=6,
х=1.
Відповідь: (1; 6)
12.
Спосіб порівняння (алгоритм)• Виразити у через х (або х через у) в кожному
рівнянні
• Прирівняти
вирази,
одержані
для
однойменних змінних
• Розв'язати
одержане рівняння і знайти
значення однієї змінної
• Підставити значення знайденої змінної в
один з виразів для іншої змінної і знайти її
значення
• Записати відповідь: х=…; у=…,або(х;у) .
13.
Розв’язати систему лінійнихрівнянь способом порівняння:
Відповідь:
14.
Розв’язати систему лінійнихрівнянь способом порівняння:
{
Відповідь:
15.
Розв’язати систему лінійнихрівнянь способом порівняння:
Відповідь:
16.
Розв’язати систему лінійнихрівнянь способом порівняння:
Відповідь:
17.
Розв”язування системи рівняньспособом додавання
Урівнюємо
модулі
коефіцієнтів
перед у
7х+2у=1, ||·(-3)
17х+6у=-9;
Додамо рівняння
+
-21х-6у=-3,
17х+6у=-9;
____________
- 4х = - 12,
7х+2у=1;
х=3,
7х+2у=1;
х=3,
7·3+2у=1;
почленно
х=3,
21+2у=1;
Розв”яжемо
рівняння
х=3,
2у=-20;
Підставимо
Розв”яжемо
рівняння
х=3,
у=-10.
Відповідь: (3; - 10)
18.
Спосіб додавання (алгоритм)• Урівняти модулі коефіцієнтів при будь – якій
змінній
• Додати почленно рівняння системи
• Утворити нову систему: одне рівняння нове,
друге - одне із старих
• Розв'язати нове рівняння і знайти значення
однієї змінної
• Підставити значення знайденої змінної в
старе рівняння і знайти значення другої змінної
• Записати відповідь: х=…; у=…,або(х;у) .
19.
Розв’язати системулінійних рівнянь способом
додавання:
Відповідь:
20.
Розв’язати систему лінійнихрівнянь способом додавання:
Відповідь:
21.
Розв’язати систему лінійнихрівнянь способом додавання:
Відповідь:
22.
Розв’язати систему лінійнихрівнянь способом додавання:
Відповідь:
23.
Розв"язування системиспособом підстановки
Виразимо у через х
у - 2х=4,
7х - у =1;
у=2х+4,
7х - у=1;
Підставимо
у=2х+4,
х=1;
Підставимо
у=2х+4,
7х - (2х+4)=1;
Розв’язуємо
рівняння
у=6,
х=1.
Відповідь : ( 1;6 )
7х - 2х - 4 = 1;
5х = 5;
х=1;
24.
Спосіб підстановки(алгоритм)
• З якого-небудь одну змінну через іншу
рівняння виразити
• Підставити одержаний вираз для змінної
в друге рівняння і розвязати його
• Зробити підстановку одного значення
змінної і обчислити значення другої
змінної
• Записати відповідь: х=…; у=… ,або(х;у).
25.
Розв’яжіть систему лінійнихрівнянь способом підстановки:
Відповідь:
26.
Розв’яжіть систему лінійних рівняньспособом підстановки:
Відповідь:
27.
Розв’яжіть систему лінійнихрівнянь способом підстановки:
{
Відповідь:
28.
Розв’яжіть систему лінійнихрівнянь способом підстановки:
{
Відповідь:
29.
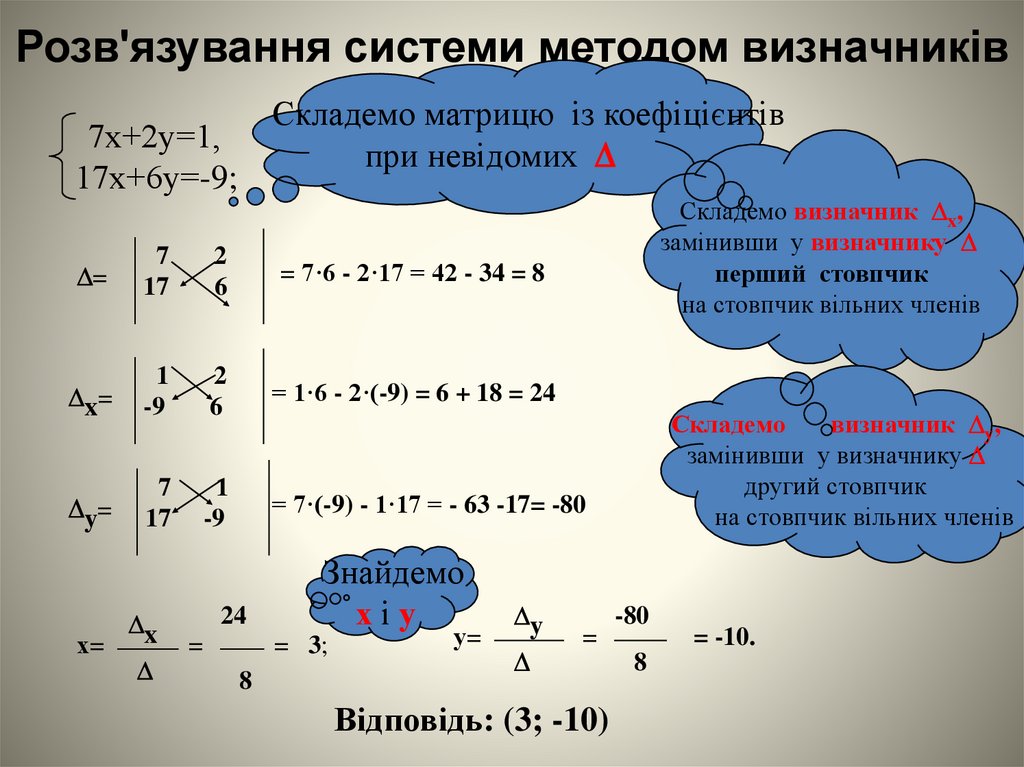
Розв'язування системи методом визначниківСкладемо матрицю із коефіцієнтів
при невідомих
7х+2у=1,
17х+6у=-9;
Складемо визначник x,
замінивши у визначнику
перший стовпчик
на стовпчик вільних членів
=
7
17
2
6
= 7·6 - 2·17 = 42 - 34 = 8
x=
1
-9
2
6
= 1·6 - 2·(-9) = 6 + 18 = 24
y=
7
17
1
-9
= 7·(-9) - 1·17 = - 63 -17= -80
х=
x
24
=
Знайдемо
хіу
= 3;
8
у=
y
=
Відповідь: (3; -10)
Складемо
визначник y,
замінивши у визначнику
другий стовпчик
на стовпчик вільних членів
-80
8
= -10.
30.
Метод визначників (алгоритм)• Складемо табличку (матрицю) коефіцієнтів невідомих і
обчислимо визначник .
• Знайдемо визначник x, одержаний із заміною
першого стовпчика на стовпчик вільних членів.
• Знайдемо визначник y, одержаний заміною другого
стовпчика на стовпчик вільних членів. із
• Знайти значення змінної х за формулою x / .
• Знайти значення змінної у за формулою y / .
• Записати відповідь: х=…; у=…,або(х;у) .
31.
Розв'язати систему лінійнихрівнянь методом визначників:
Відповідь:
32.
Розв'язати систему лінійнихрівнянь методом визначників:
Відповідь:
33.
Розв'язати систему лінійнихрівнянь методом визначників:
Відповідь:
34.
Розв'язати систему лінійнихрівнянь усіма способами:
Відповідь:
35.
Розв'язати систему лінійнихрівнянь усіма способами:
Відповідь:
36.
Розв'язати систему лінійнихрівнянь усіма способами:
Відповідь:
37.
Розв'язати систему лінійнихрівнянь усіма способами:
Відповідь:
38.
На уроці я- дізнався...
- зрозумів...
- навчився...
- найбільший мій успіх - це...
- найбільші труднощі я відчув...
- я не вмів, а тепер умію...
- я змінив своє ставлення до...
- на наступному уроці я хочу...
39.
40.
1.Янченко Г., Янченко В.,Янченко О.Алгебра 7 клас: Книга для вчителя .2.Когдратьєва Л., Тепцова О. Збірник контрольних і самостійних робіт з
алгебри для поточного оцінювання навчальних досягнень учнів.7 клас.
3.Вихор С. Самостійні та контрольні роботи з алгебри. 7 клас.
4.Олійник Л.Довідник-помічник з алгебри 7 клас.
5.Возняк Г.,Возняк О.Тестові завдання з алгебри. 7 клас
6.Гап‘юк Г.,Мартинюк С.,Чиж О.Вчимося розв’язувати задачі з алгебри.7 клас



































 mathematics
mathematics