Similar presentations:
Измерительные работы. Урок геометрии в 9 классе
1.
Измерительныеработы
Урок геометрии в 9 классе
2. Цель урока
Познакомить учащихся сизмерительными работами на
местности, основанными на
использовании теорем синусов и
косинусов
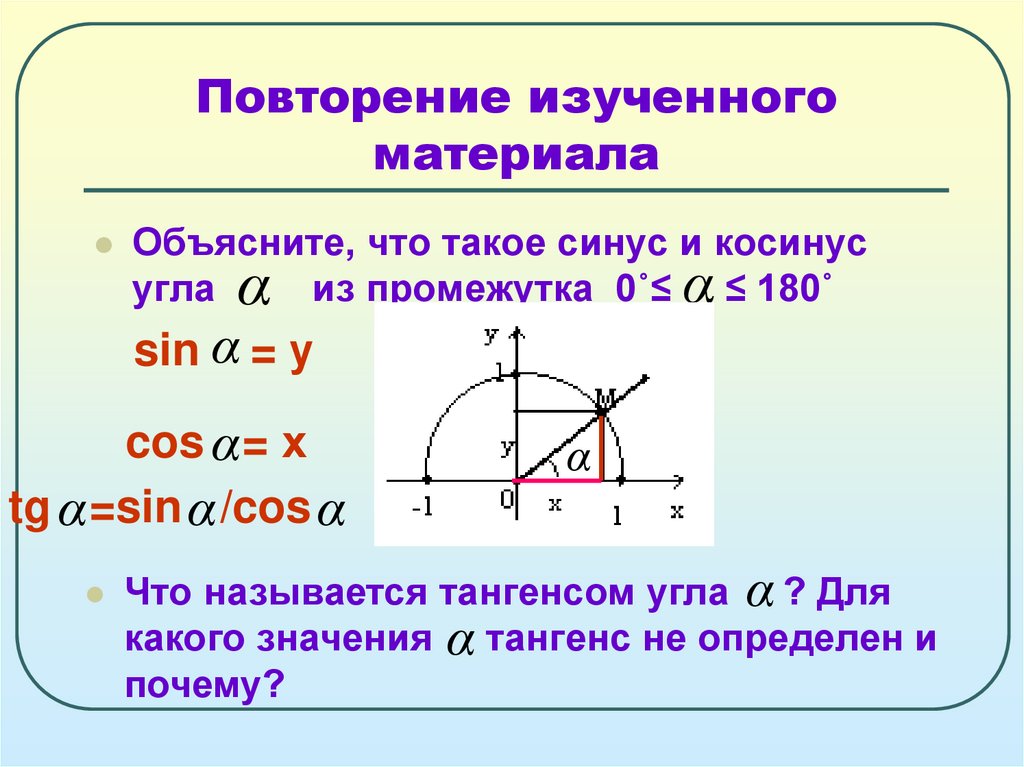
3. Повторение изученного материала
Объясните, что такое синус и косинусугла
из промежутка 0˚≤ α ≤ 180˚
α
sin α = у
cos α= х
tg α =sin α /cos α
α
Что называется тангенсом угла α ? Для
какого значения α тангенс не определен и
почему?
4.
Повторение изученногоматериала
Назовите основное
тригонометрическое тождество
sin α + cos α = 1
2
2
Напишите формулы приведения
sin( 90° α) = cos α
sin( 90° + α) = cos α
sin( 180° α) = sin α
tg (90° α) = ctgα
tg (180° α) = tgα
cos(90° α) = sin α
cos(90° + α) = sin α
cos(180° α) = cos α
tg (90° + α) = ctgα
5.
Повторение изученногоматериала
Сформулируйте теорему о площади
треугольника
absin α
S=
2
Сформулируйте теорему синусов
a
b
c
=
=
sin A sin B sin C
Сформулируйте теорему косинусов
2
2
a =b +c
2
2bc cos A
6.
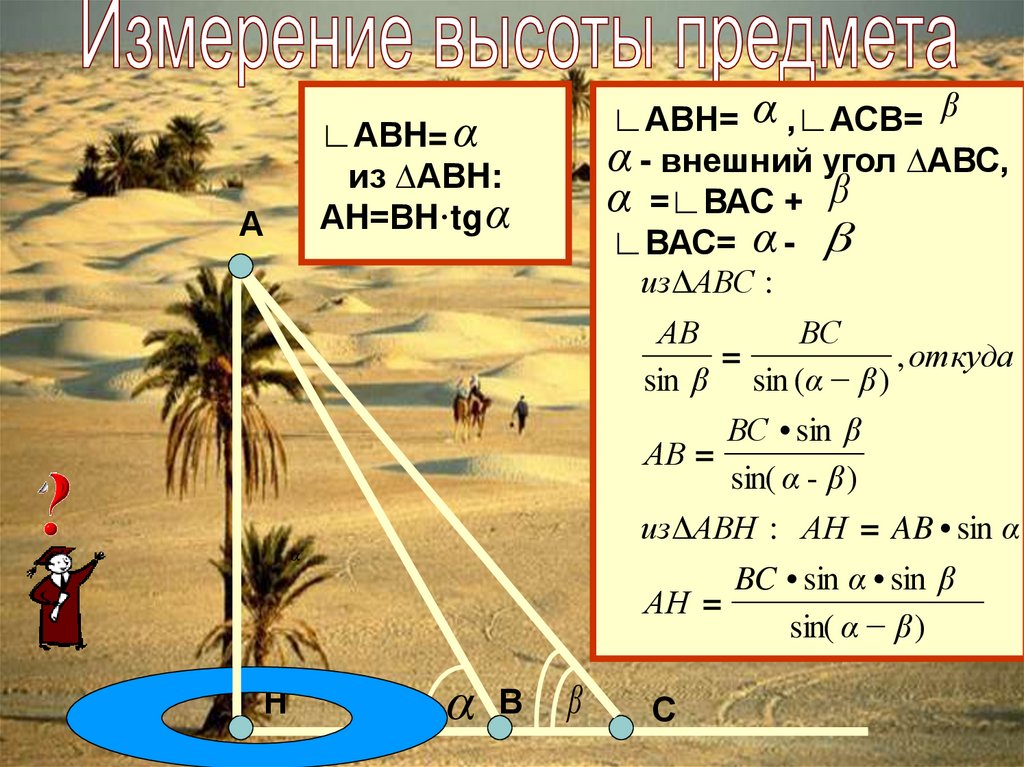
∟АВН= α ,∟АСВ= βα - внешний угол ∆АВС,
α =∟ВАС + β
∟ВАС= α - β
изΔАВС :
ВС
АВ
, откуда
=
sin β sin (α β )
ВС • sin β
АВ =
sin( α - β )
изΔАВH : АH = AB • sin α
BC • sin α • sin β
АH =
sin( α β )
∟АВH= α
из ∆АВH:
АH=ВH·tg α
А
α
Н
α
В
β
С
7.
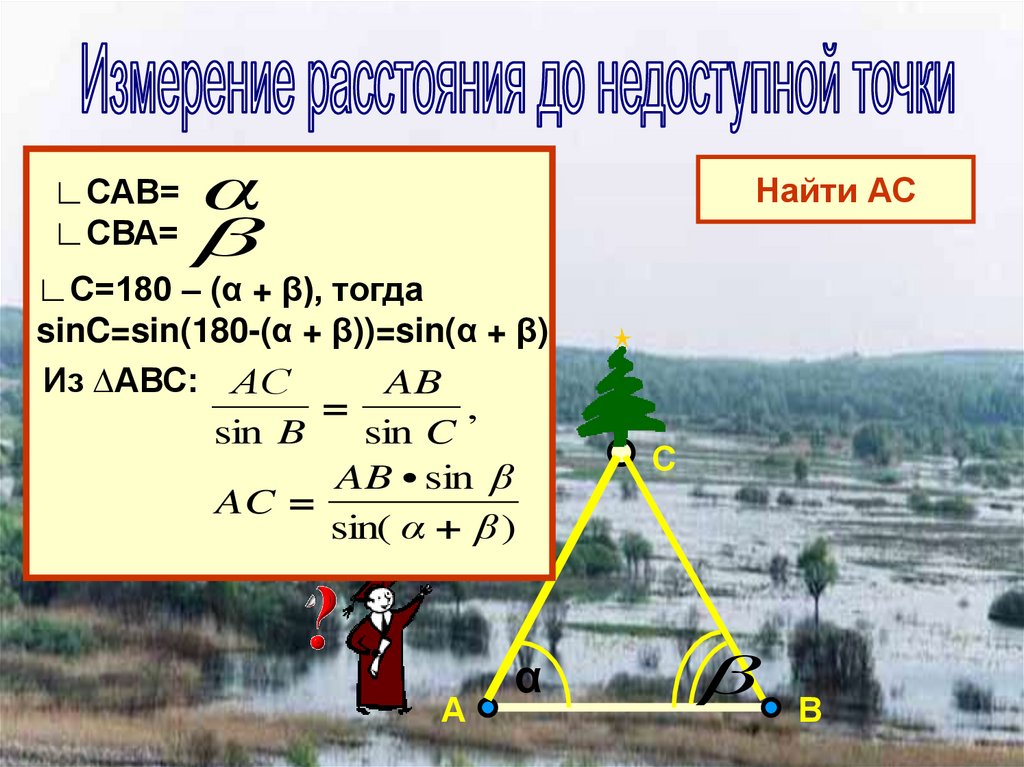
∟САВ=∟СВА=
α
Найти АС
β
∟С=180 – (α + β), тогда
sinC=sin(180-(α + β))=sin(α + β)
Из ∆АВС: АС
AB
=
,
sin Bα
sin C
AB • sin β
AC =
sin( α + β )
А
α
С
β
В
8.
СЗадача №1036
N
45°
М
10°
50м
А
Найти СD
D
9.
10.
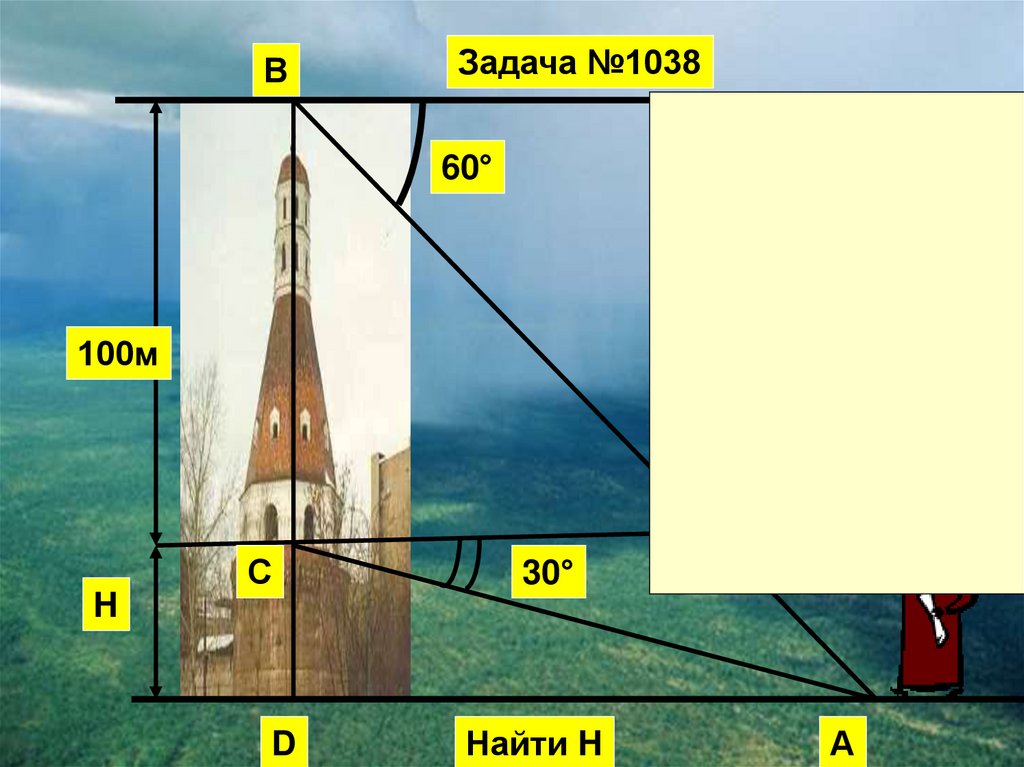
ВЗадача №1038
60°
100м
С
30°
H
D
Найти H
А
11.
12.
Домашнеезадание
П.100,
№1037,
№1034








 mathematics
mathematics








