Построение сечений многогранников

1.

2.

Вспомним сказку “Маленький принц”.
Помните, какую картинку (первую в
своей жизни) нарисовал в детстве
Экзюпери? Посмотрите на нее, что там
изображено?
Как ни странно все думают, что это
шляпа. Но на самом деле это был удав,
проглотивший слона. Чтобы другие это
поняли, юный художник выразился
конкретнее и нарисовал второй рисунок.
Он был уверен, что теперь-то все
поймут, так как он объяснил взрослым
свою картинку не только снаружи, но и
изнутри.
Как же это удалось шестилетнему
художнику — будущему знаменитому
писателю и летчику?
Он мысленно разрезал удава-шляпу и
показал, что содержится внутри.

3.

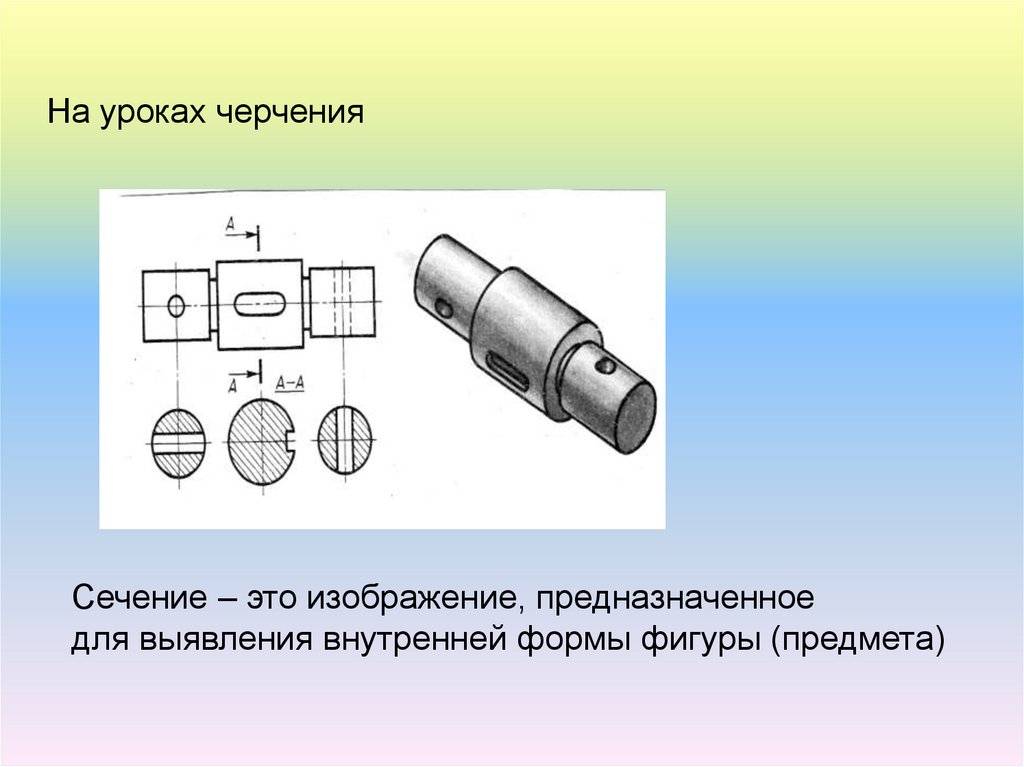
На уроках черчения
Сечение – это изображение, предназначенное
для выявления внутренней формы фигуры (предмета)

4.

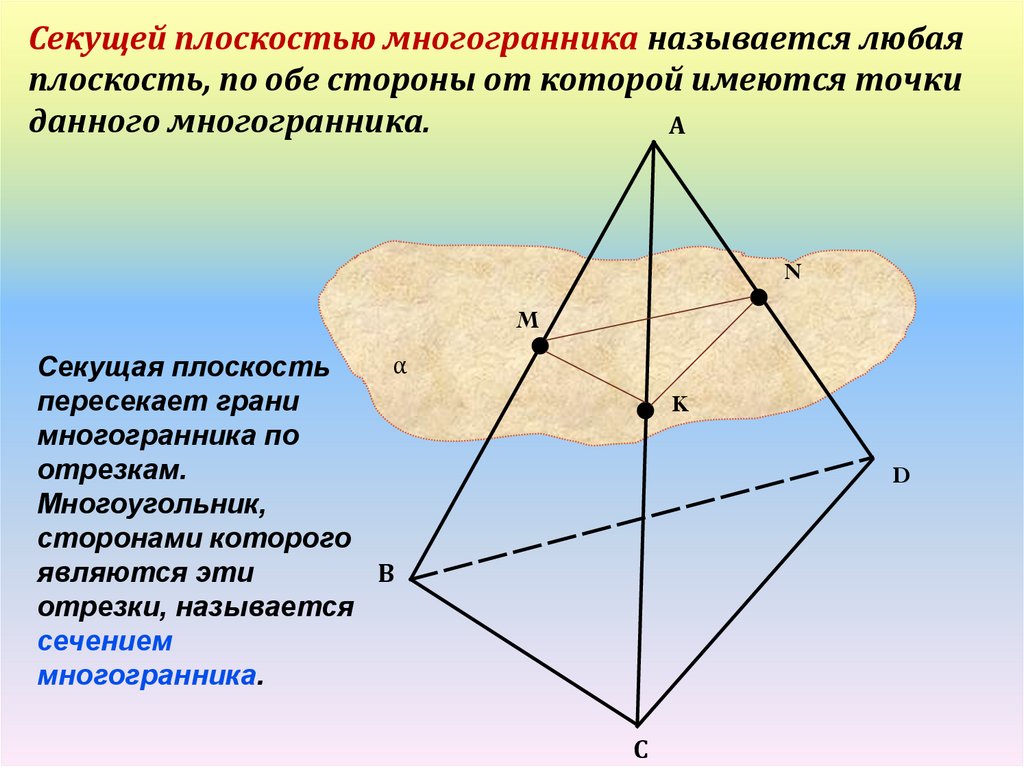
Секущей плоскостью многогранника называется любая
плоскость, по обе стороны от которой имеются точки
данного многогранника.
А
N
M
α
Секущая плоскость
пересекает грани
многогранника по
отрезкам.
Многоугольник,
сторонами которого
являются эти
В
отрезки, называется
сечением
многогранника.
K
D
С

5.

Аксиомы и теоремы стереометрии
В
А
α
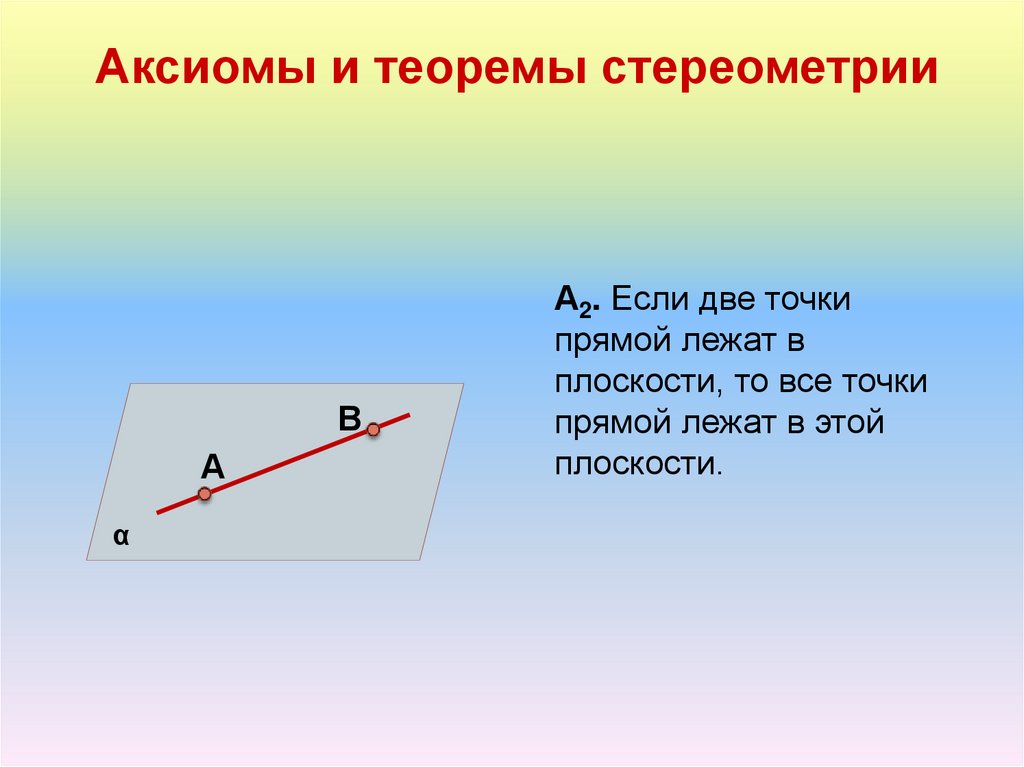
А2. Если две точки
прямой лежат в
плоскости, то все точки
прямой лежат в этой
плоскости.

6.

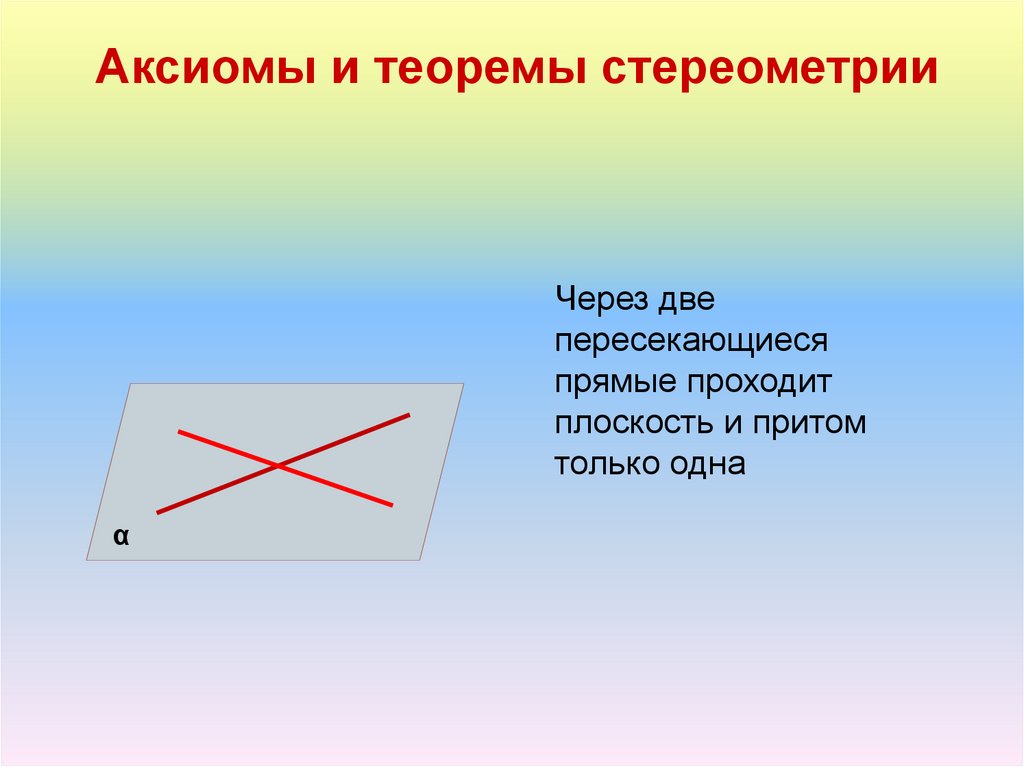
Аксиомы и теоремы стереометрии
Через две
пересекающиеся
прямые проходит
плоскость и притом
только одна
α

7.

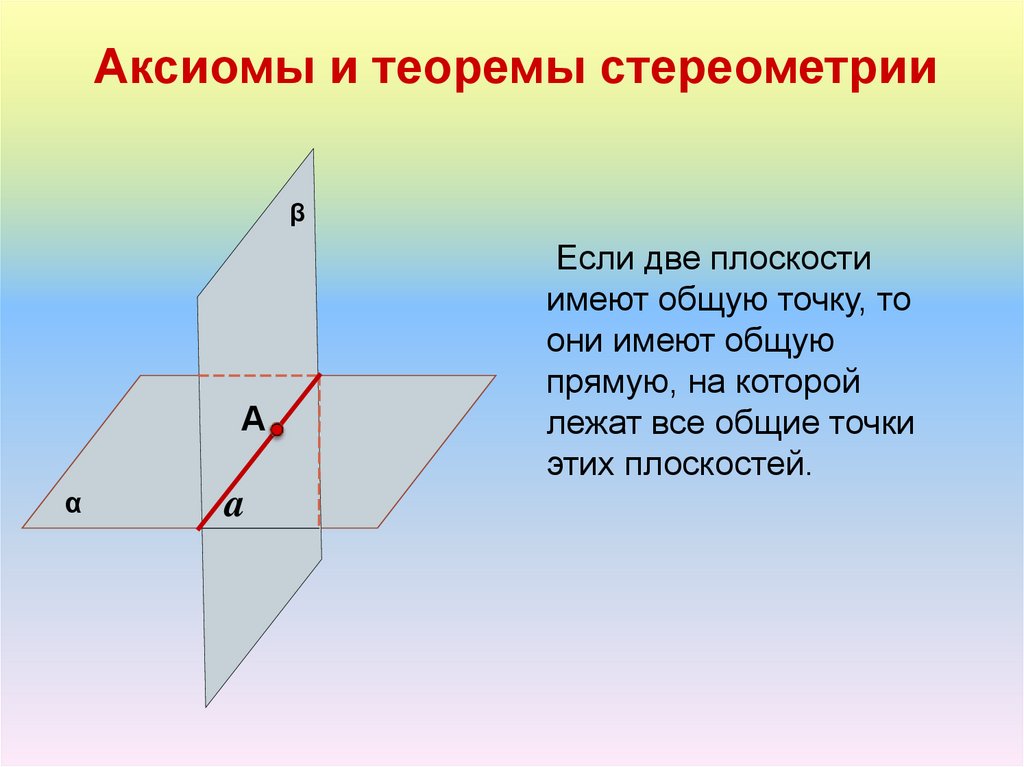
Аксиомы и теоремы стереометрии
β
А
α
a
Если две плоскости
имеют общую точку, то
они имеют общую
прямую, на которой
лежат все общие точки
этих плоскостей.

8.

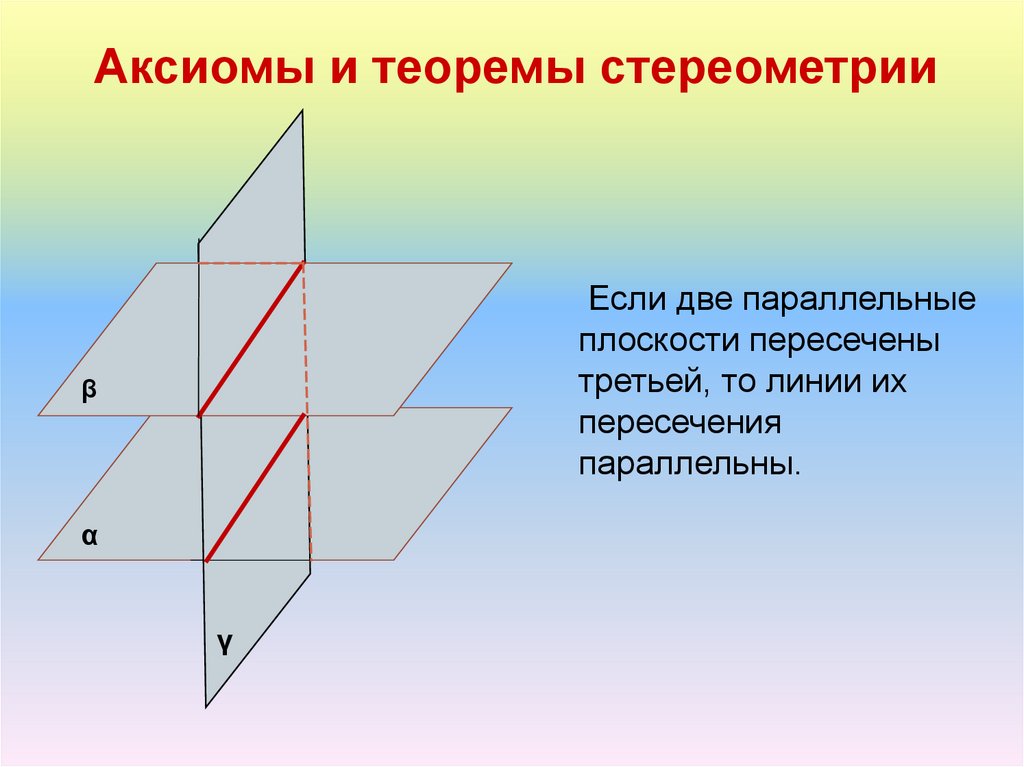
Аксиомы и теоремы стереометрии
Если две параллельные
плоскости пересечены
третьей, то линии их
пересечения
параллельны.
β
α
γ

9.

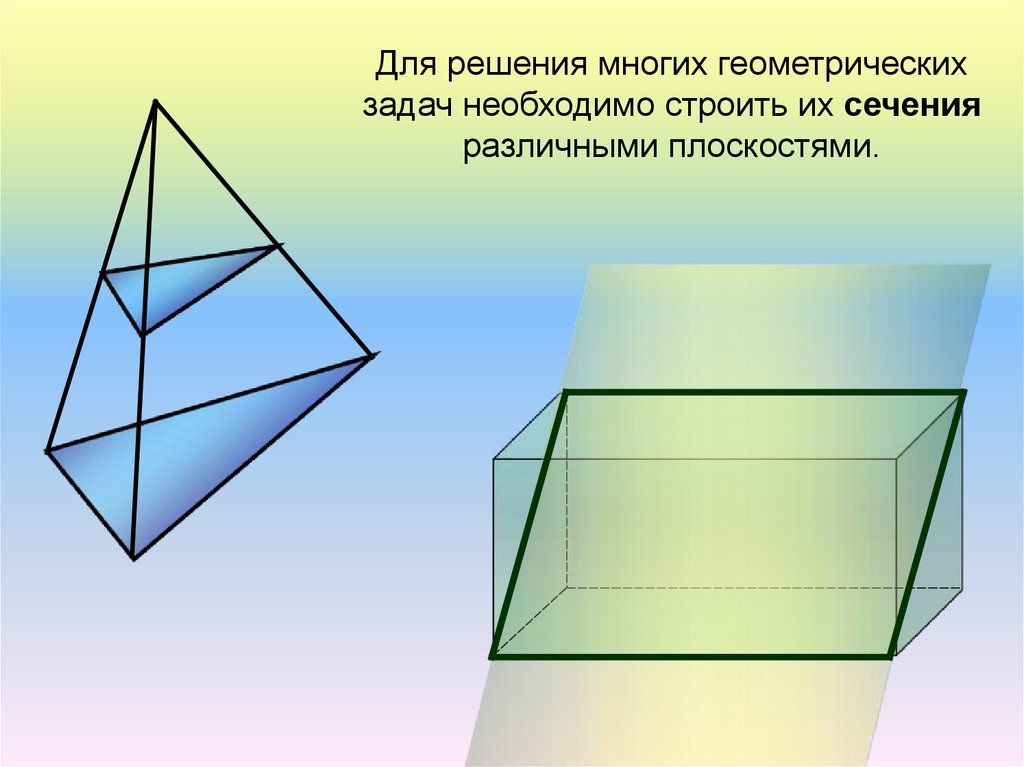
Для решения многих геометрических
задач необходимо строить их сечения
различными плоскостями.

10.

Для построения сечения нужно построить
точки пересечения секущей плоскости с
ребрами и соединить их отрезками.
1. Соединять можно только две точки, лежащие в
плоскости одной грани.
2. Секущая плоскость пересекает
грани по параллельным отрезкам.
параллельные
3. Если в плоскости грани отмечена только одна точка,
принадлежащая плоскости сечения, то надо построить
дополнительную точку. Для этого необходимо найти
точки пересечения уже построенных прямых с другими
прямыми, лежащими в тех же гранях.

11.

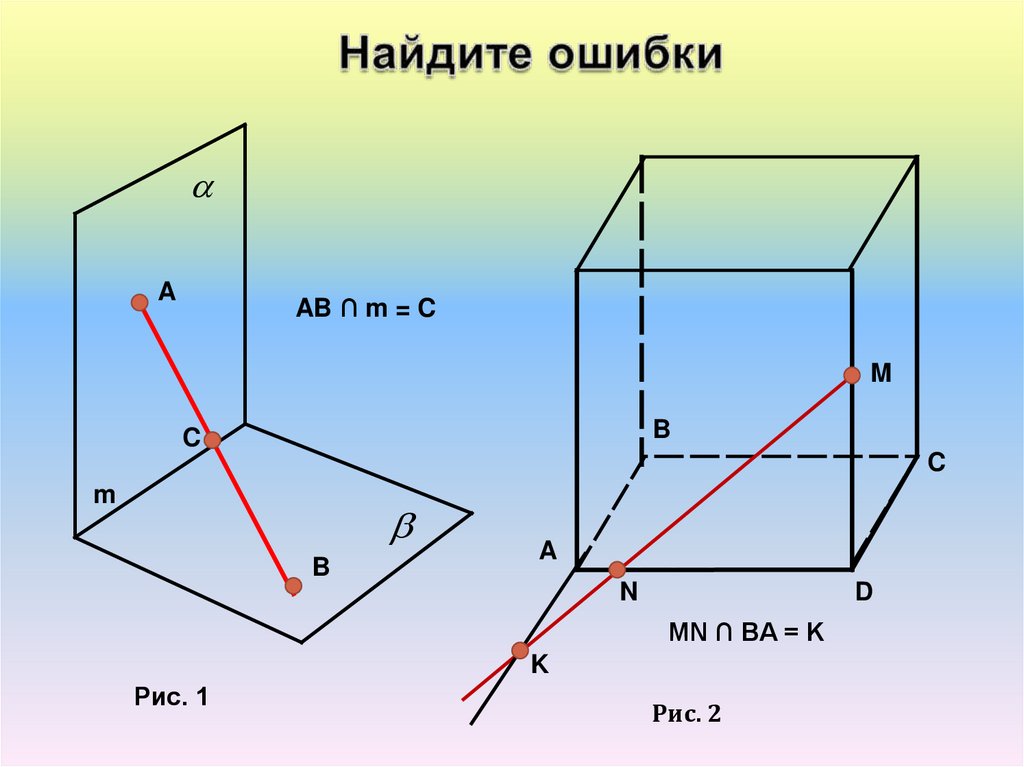
A
AB ∩ m = C
M
B
C
C
m
B
A
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2

12.

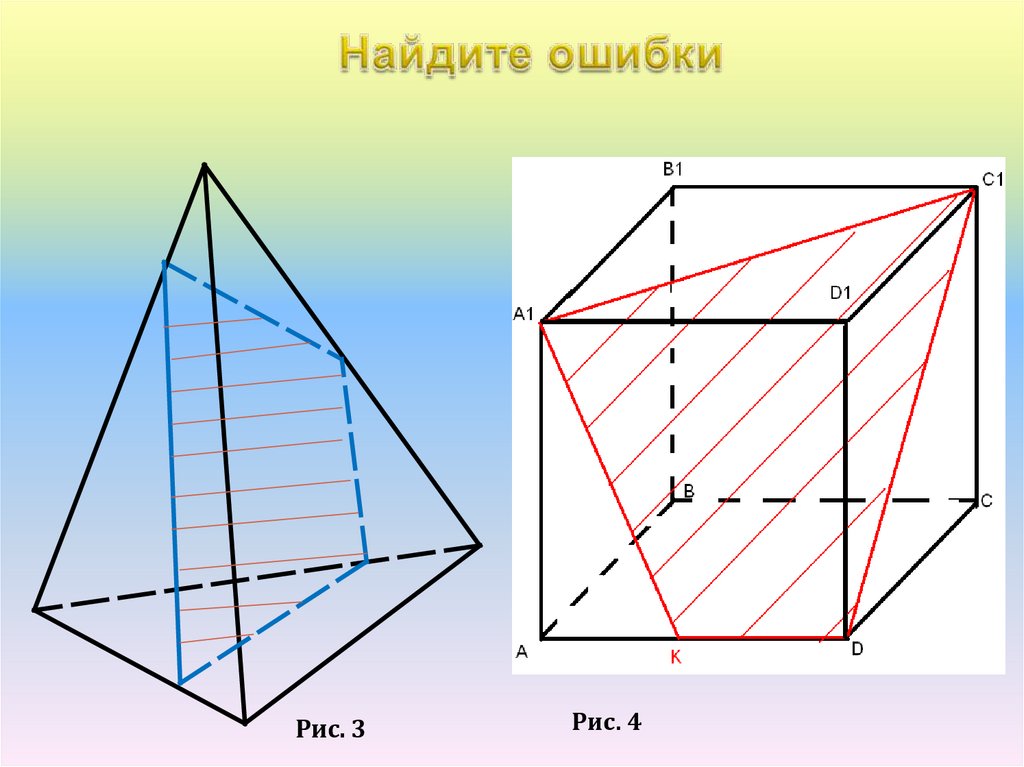
Рис. 3
Рис. 4

13.

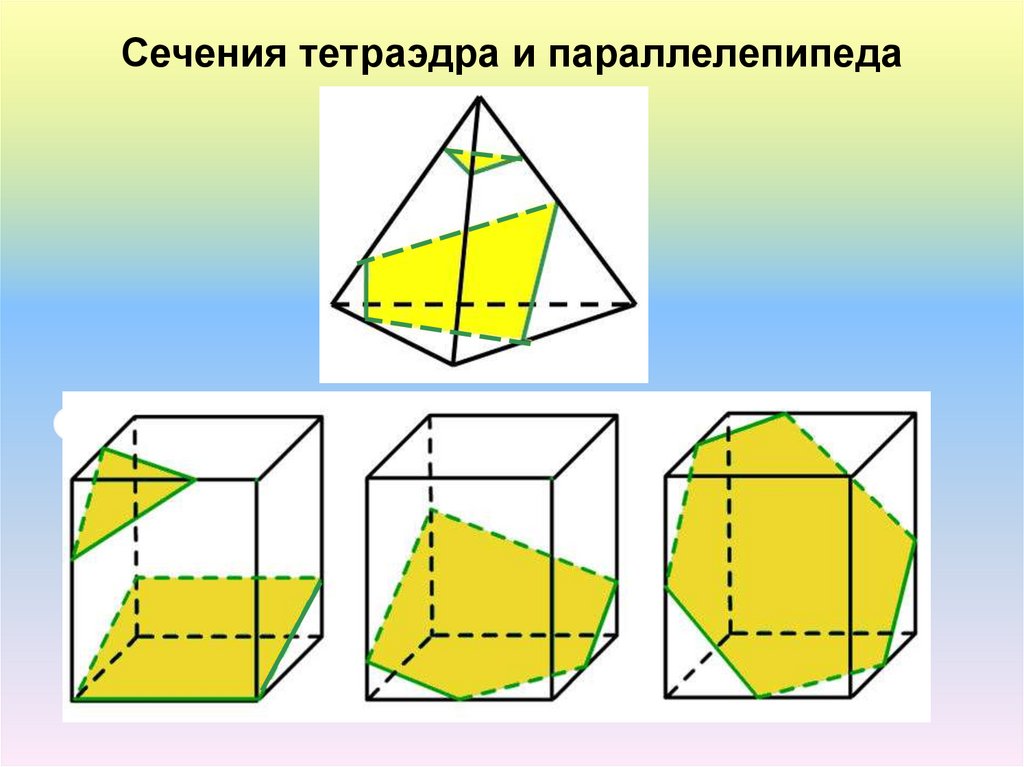
Сечения тетраэдра и параллелепипеда

14.

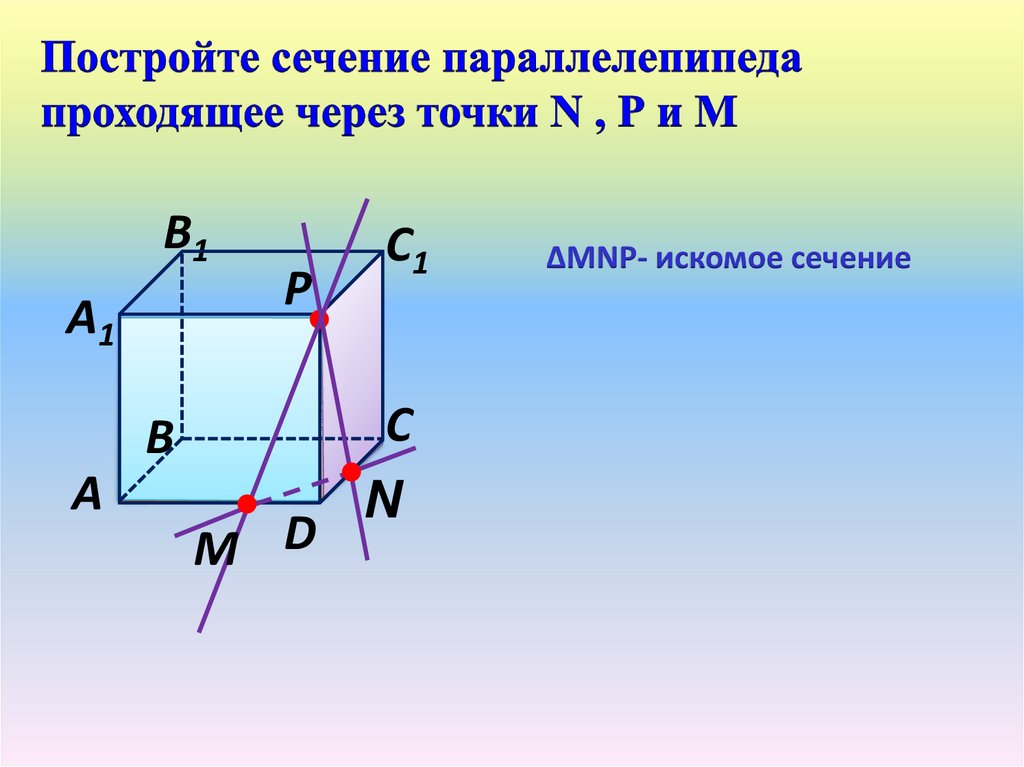
В1
А1
Р
В
А
М D
С1
С
N
∆МNР- искомое сечение

15.

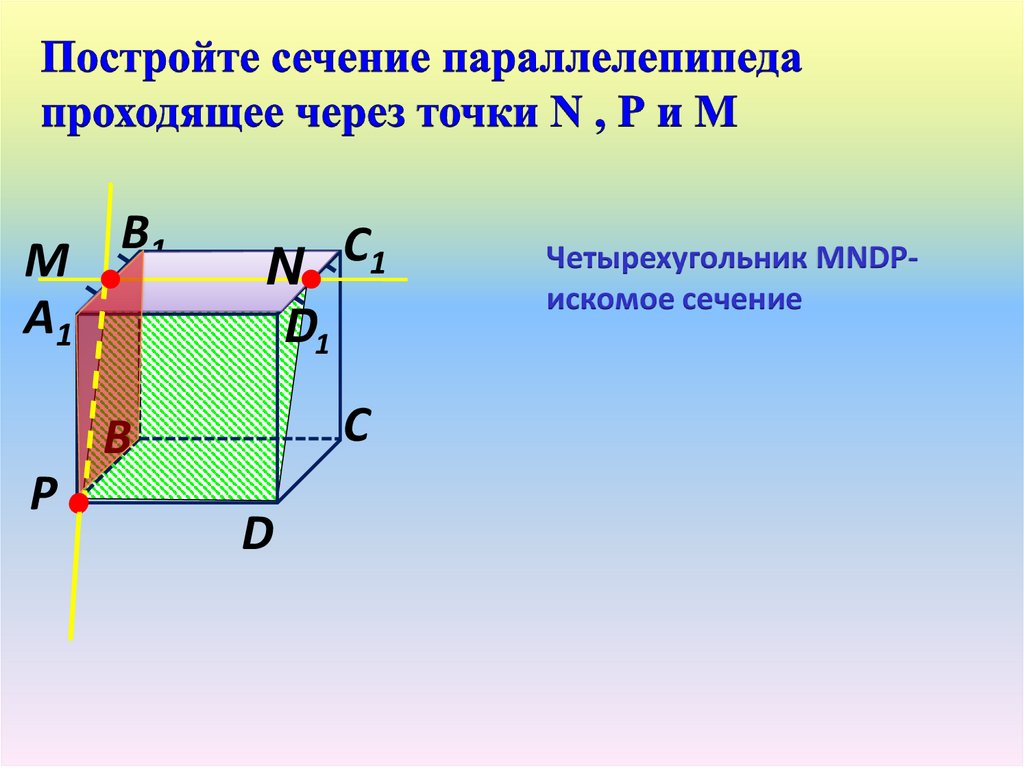
М
А1
В1
С
N 1
D1
С
В
Р
D
Четырехугольник МNDРискомое сечение

16.

К
В1
А1
А
N
В
М
D1
Р
D
С1
Н
С
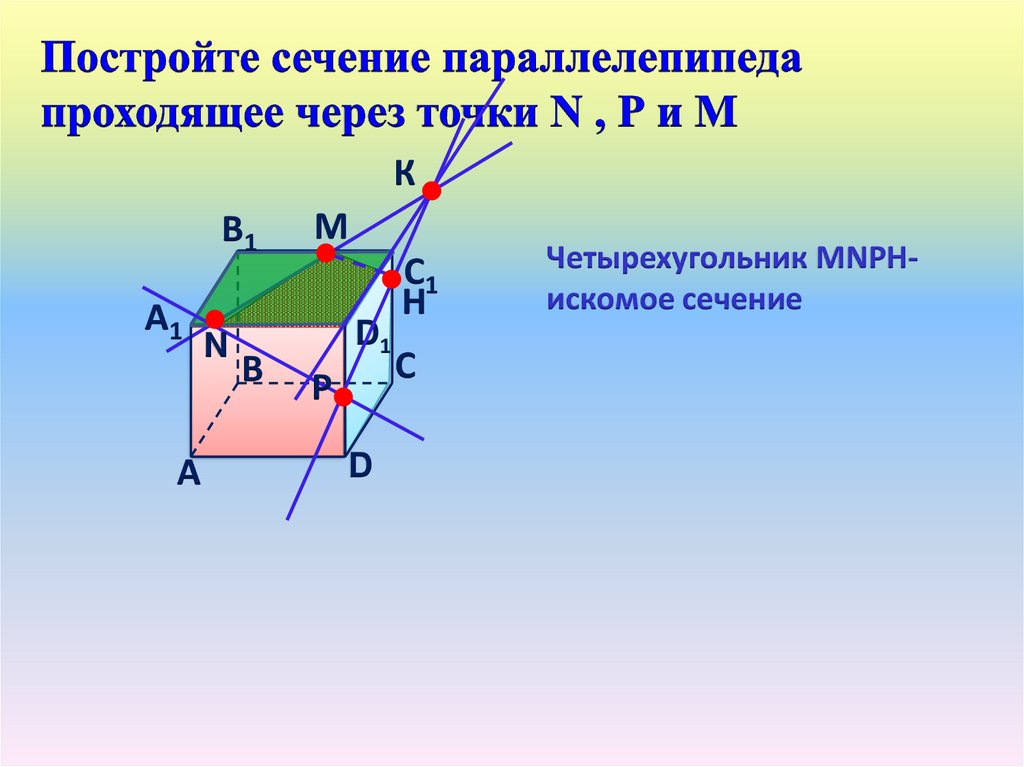
Четырехугольник МNРНискомое сечение

17.

В1
С1
А1
М
N
В
А
К
Н
Р
D1
С
D
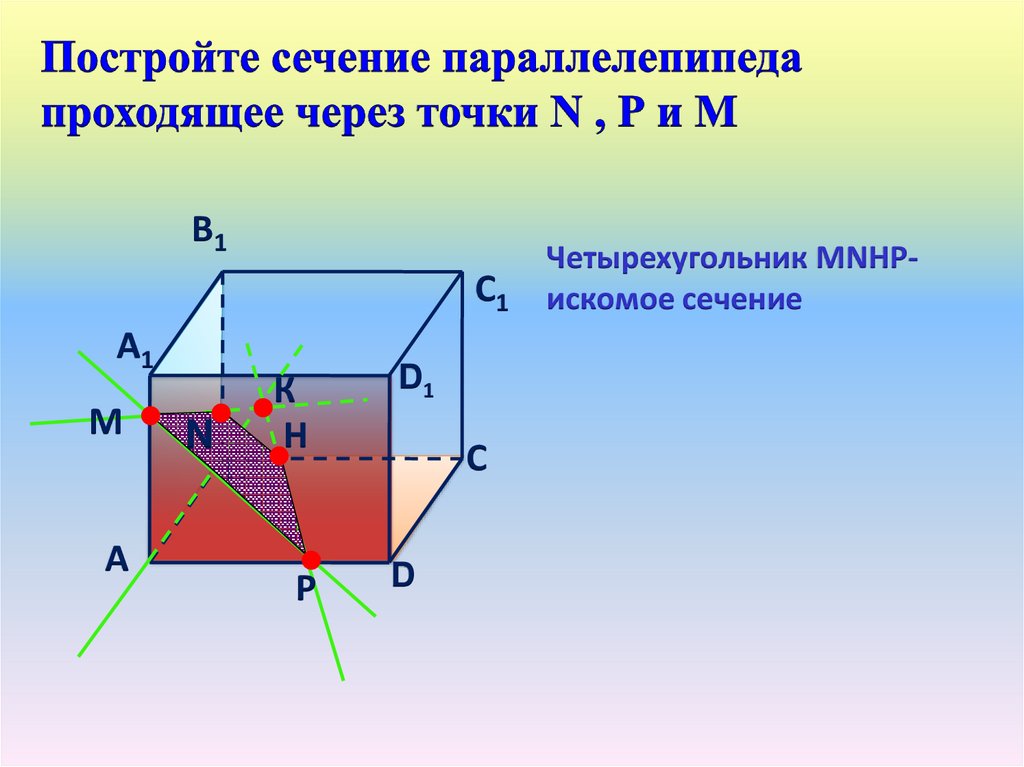
Четырехугольник МNНРискомое сечение

18.

Р
С1
А1
М
А
К
D1
В
N
С
Т
Н
D
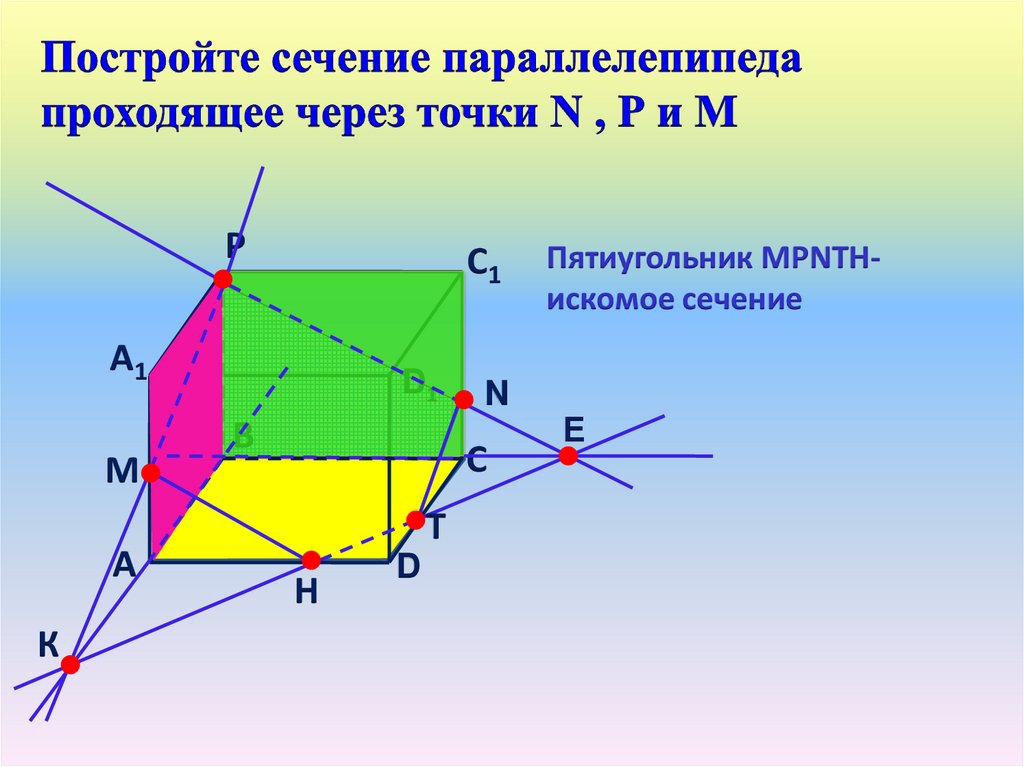
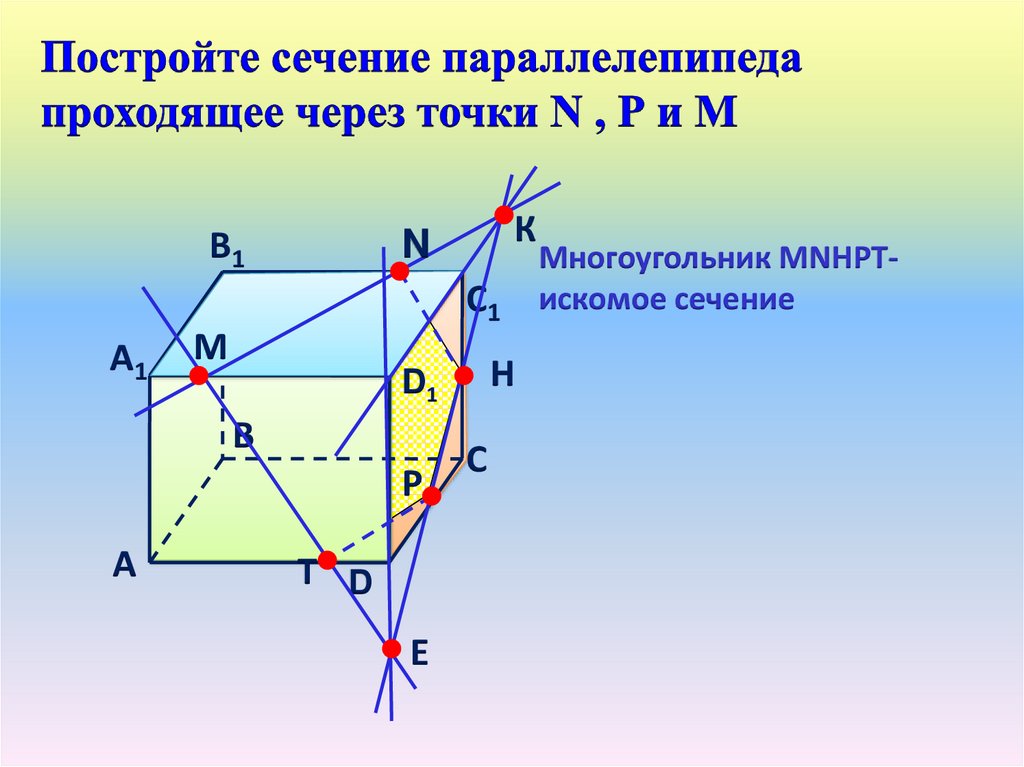
Пятиугольник МРNТНискомое сечение
Е

19.

В1
А1
D1
Т
В
Е
А
Р
С
N
Н
М К
D
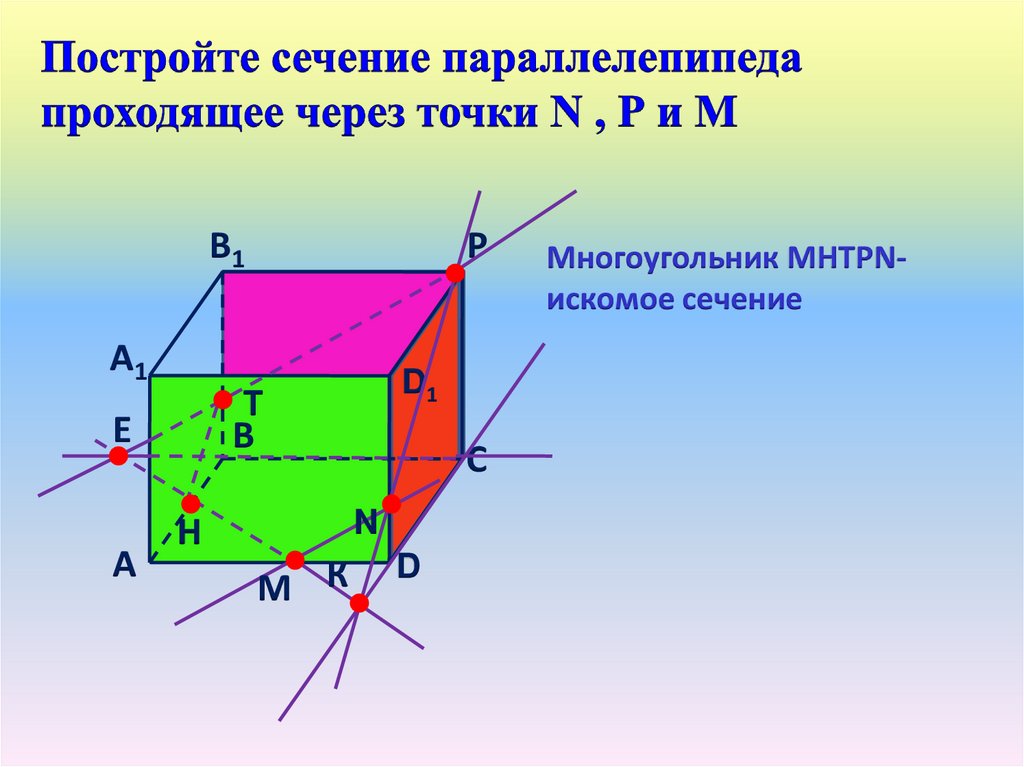
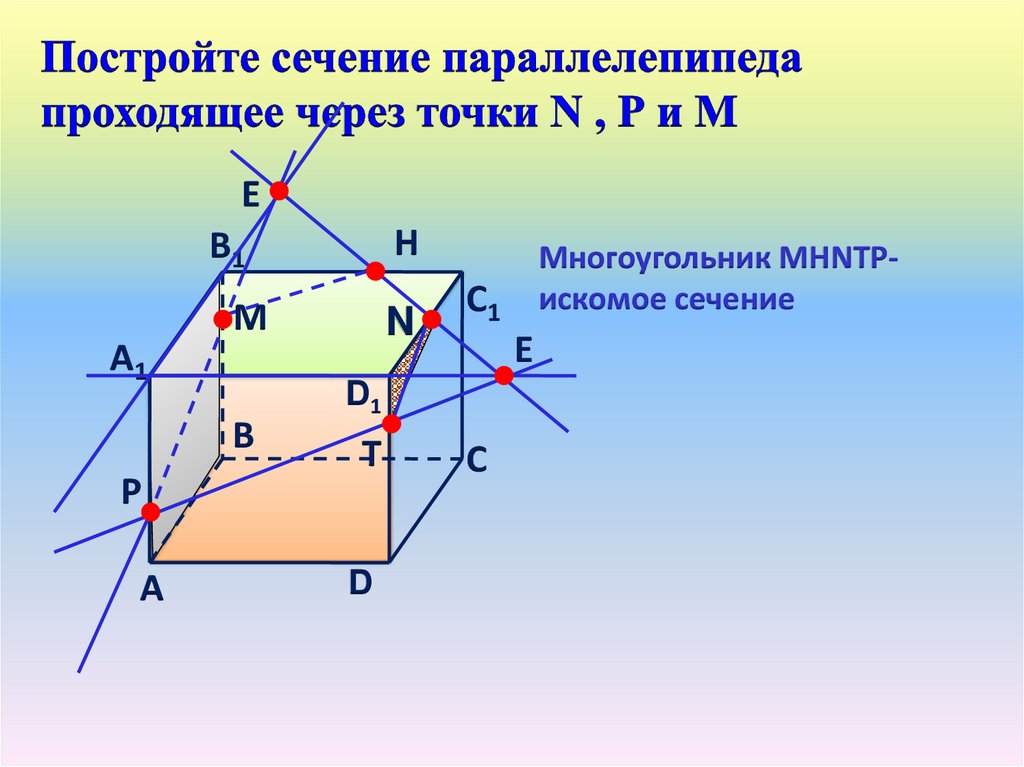
Многоугольник МНТРNискомое сечение

20.

В1
К
N
С1
А1
М
В
Р
А
Н
D1
Т D
Е
С
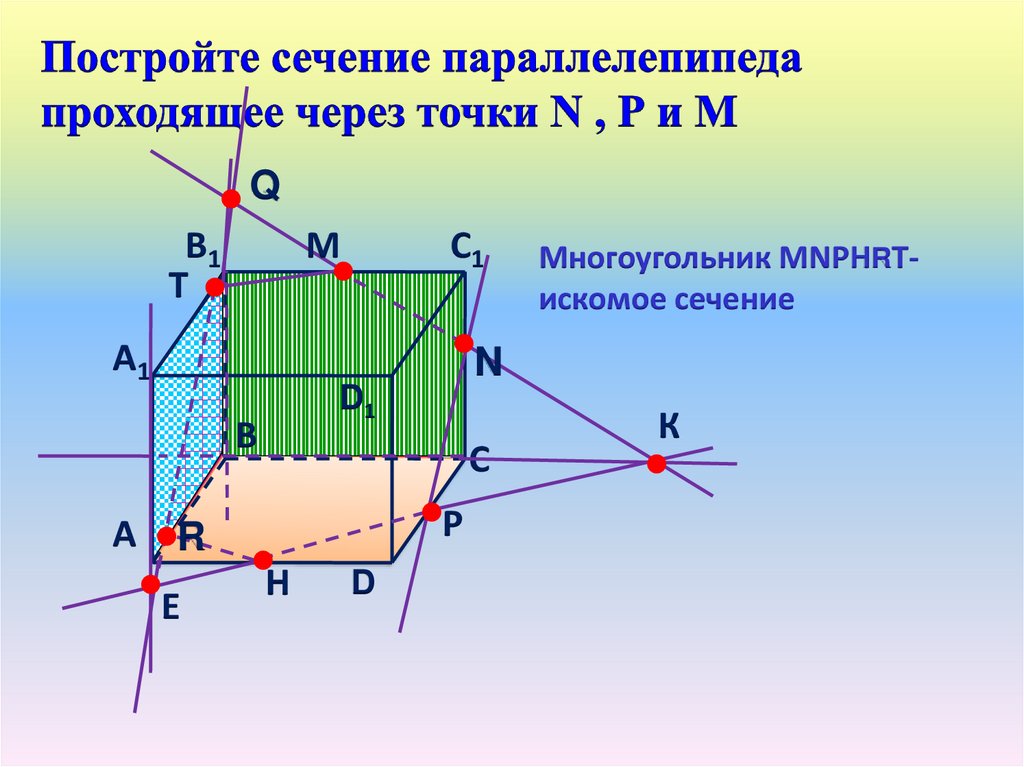
Многоугольник МNНРТискомое сечение

21.

Е
Н
В1
М
А1
В
Р
А
N
С1
Е
D1
Т
D
Многоугольник МНNТРискомое сечение
С

22.

Е
В1
Н К
А1 N
В
А
F
Р
D1
М
O
D
Т
С1
С
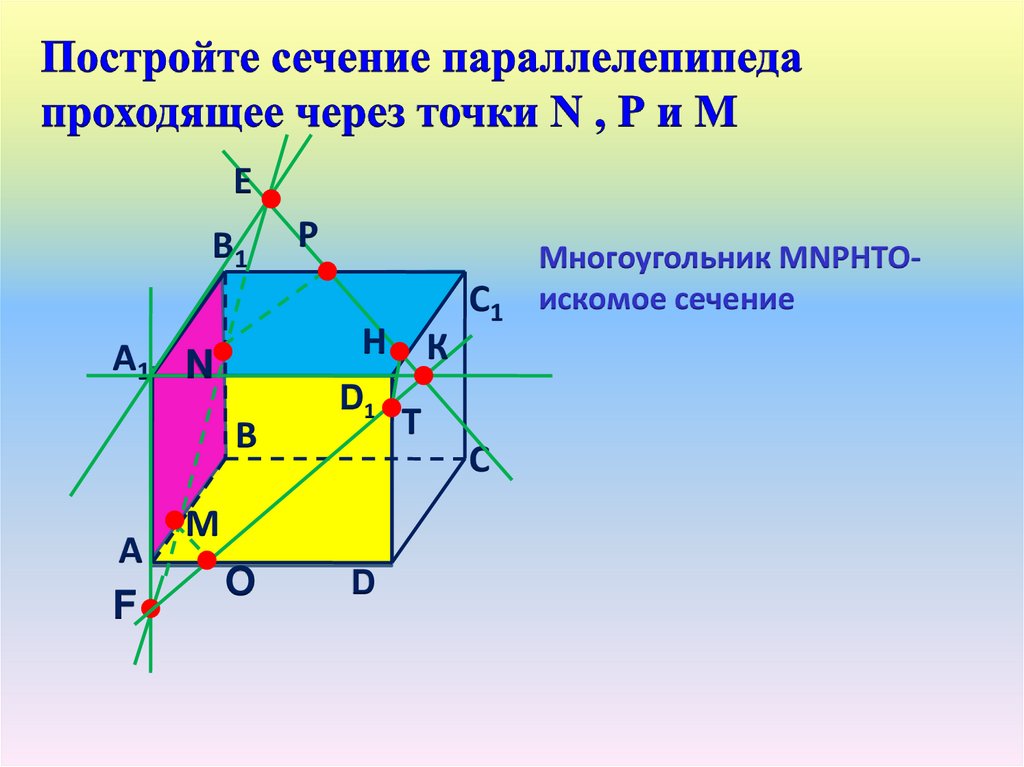
Многоугольник МNРНТОискомое сечение

23.

Е
В1
А1
N
Р
Н
В
D1
М
А
К
Т
D
R
С1
S
С
Многоугольник МНNРRТискомое сечение

24.

Q
В1
Т
М
А1
Многоугольник МNРНRТискомое сечение
N
D1
В
А
С1
С
Р
R
Е
Н
D
К

25.

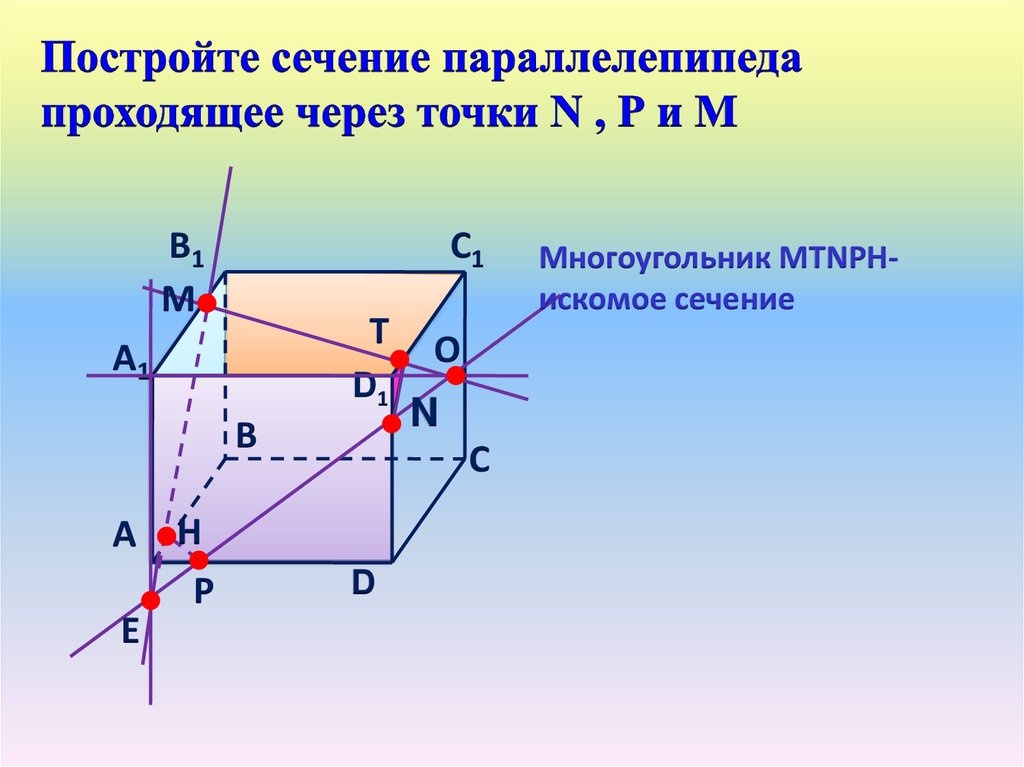
В1
М
С1
Т
А1
D1
В
А
Е
Н
Р
О
N
С
D
Многоугольник МТNРНискомое сечение

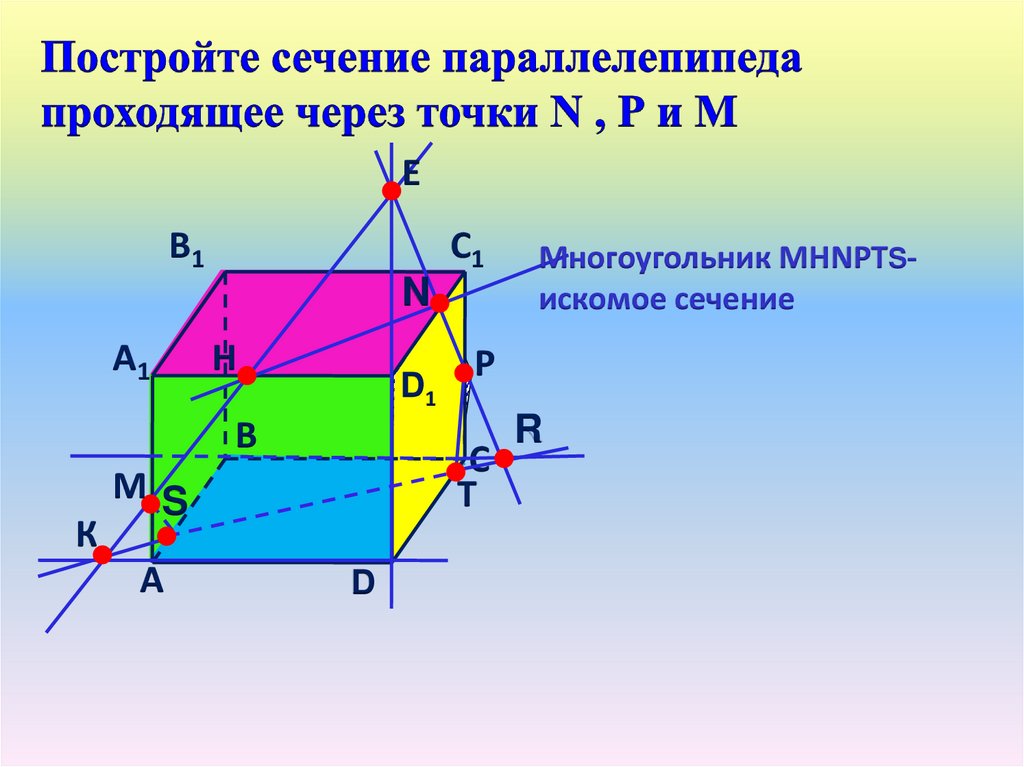
26.

Е
В1
С1
N
А1
Н
D1
В
К
А
Р
С
Т
МS
D
Многоугольник МНNРТSискомое сечение
R

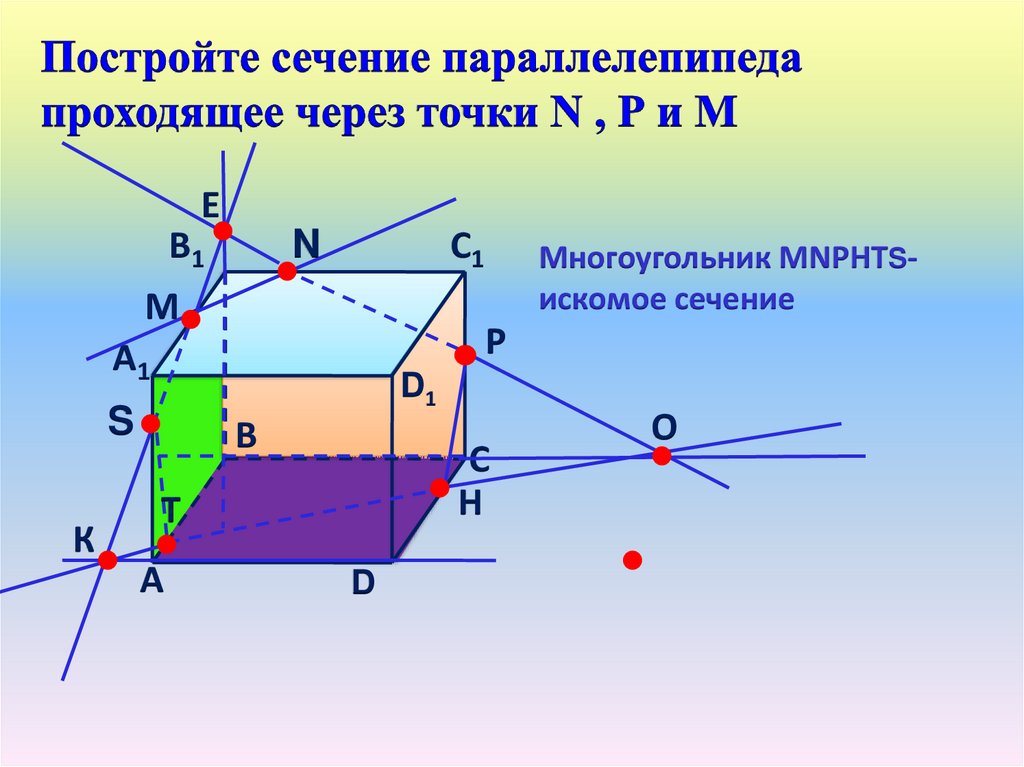
27.

Е
В1
С1
N
М
Р
А1
D1
S
К
Многоугольник МNРНТSискомое сечение
В
С
Н
Т
А
D
О