Аэрогазодинамика. Плоские изоэнтропические течения газа (лекции 8, 9)

1. Плоские изоэнтропические течения газа

Аэрогазодинамика
Плоские изоэнтропические
течения газа
Лекции 8,9

2.

В пространстве движущегося газа за исключением
некоторых достаточно ограниченных областей
(пограничный слой, след за телом и др.), имеет
место безвихревое, или потенциальное течение.
Выясним, при каком условии течение можно
считать потенциальным, т. е. при каком условии в
потоке будут отсутствовать вихри
2

3. 8.1.Критерий потенциальности

Проведем касательную к линии тока
в точке а (совпадает с направлением
вектора V ) и внутреннюю нормаль.
Уравнение движения
в проекции на
2
V
1 dp
нормаль
r
dn
Вдоль линии тока полная удельная
энергия и энтропия не изменяют своей
величины, т. е. di0 0 и dS = 0.
Допустим, что при переходе от линии тока аА к
другой bВ полная удельная энергия и энтропия
газа изменяются. То есть
1
dp
di0 di VdV 0 и dS di 0
T
Исключив di, получим
3

4.

dp
di0 VdV TdS
1 dp di0
dV
dS
V
T
,
или
dn dn
dn
dn
Из уравнения движения имеем
dS
dV V di0
V2
di0
dV
dS
V
T
или
V
T
,
dn
r
dn
dn
r
dn
dn
dn
Выражение в скобках есть удвоенная угловая скорость . Из условия потенциальности (вращательное
dS
движение отсутствует) ω = 0, di0
T
0
следовательно
dn
dn
Таким образом, поток газа можно считать
потенциальным, если полная удельная энергия и
энтропия при переходе от одной линии тока к
другой не изменяются
di0
dS
0
0
dn
dn
4

5. 8.2.Основное дифференциальное уравнение плоского потенциального потока газа

Уравнение неразрывности для установившегося
течения плоского потенциального газового потока
Vx Vy
Vx Vy
Vy
0 . Отсюда Vx
0
x
y
y
x
y
x
Выразим плотность через проекции скорости.
Считая движение баротропным ( p) , где
p p( x, y)) , можно записать, что
d p 1 p
d p 1 p
2
2
x dp x a x
y dp y a y
p
p
Заменим
и y через уравнения Эйлера с учетом
x
малости массовых сил ( X 0 , Y 0 ):
5

6.

dp
a .
d
Vx
Vx
Vx
p
dVx
Vx
2 Vx
Vy
Vx
Vy
x
a
x
y
x
dt
x
y
2
Для проекции на ось ОY запишем аналогично. Тогда
исходное уравнение неразрывности примет вид
Vy
Vx Vy
Vx
2
2
a V x VxVy y x a Vy y 0
2
2
x
Перепишем его с учетом потенциальности течения
2
2
2
2
2
2
2
a
V
2
V
V
a
V
0
x
x y
y
2
2
x
x y
y
Это есть основное дифференциальное уравнение
газовой динамики для плоского потенциального
установившегося газового потока.
6

7.

Это нелинейное дифференциальное уравнение
второго порядка в частных производных относительно
неизвестной функции φ. Однако коэффициенты при
вторых производных в явном виде от координат х и y
не зависят, поэтому уравнение называют
квазилинейным дифференциальным уравнением.
Для решения уравнения применяют два метода:
1) метод малых возмущений (метод линеаризации),
который широко используется при исследовании
обтекания тонких тел при малых углах атаки как в
дозвуковом, так и в сверхзвуковом потоке и позволяет
получить решение в аналитическом виде;
2) метод характеристик – численный метод, который
применяется для определения поля скоростей в
сверхзвуковом потоке.
7

8. 8.3. Характеристики в плоскости потока

В каждой точке плоскости XОY можно
провести два направления линий возмущения (линий Маха). При переходе
от одной точки к другой направление
линий возмущения может изменяться,
так как значения V и a в разных точках плоскости XОY в общем случае
различны.
Найдем в плоскости такую кривую y = y (x), в каждой
точке которой направление касательной совпадает с
направлением одной из линий возмущения для данной точки. Такую кривую называют характеристикой.
tg tg
1
V2
1,
Из рисунка tg tg
(*),
2
tg
a
1 tg tg
dy
Vy
tg
tg
и
. Тогда равенство (*) запишем в виде
Vx
dx
8

9.

Vy dy
dy Vy
V2
. И после преобразований
1 1
2
a
Vx dx
dx Vx
2
dy
dy
2
2
Vx a dx 2VxVy dx Vy2 a 2 0
Решение этого уравнения представляет собой
дифференциальные уравнения характеристик
в плоскости потока:
2
2
dy VxVy a V a
dx
Vx2 a 2
Сверхзвуковой поток V a - два различных вещественных корня. Через каждую точку плоскости можно
провести два элемента характеристик; всю плоскость
можно покрыть двумя семействами характеристик.
Уравнение является уравнением гиперболического
типа.
9

10.

Для определенности интегральные кривые y = y(x),
соответствующие решению со знаком «+», называют
характеристиками первого семейства, а со знаком
«–» – характеристиками второго семейства.
Для звукового потока V a - один вещественный
корень и одно семейство характеристик; уравнение
параболического типа.
Для дозвукового потока ( V a ) вещественных корней
и характеристик нет; уравнение эллиптического
типа.
10

11. 8.4.Характеристики в плоскости годографа скорости

dVy
1
1
,
dy
m2
dVx I
dx 2
dVy
1
1
.
m1
dy
dVx II
dx 1
Зависимости для расчета изменения скорости течения
газа вдоль характеристик в плоскости потока (в
физической плоскости)
11

12.

Характеристики в физической плоскости и в плоскости
годографа скорости перпендикулярны друг другу.
Характеристики первого семейства в плоскости XY
перпендикулярны характеристикам второго семейства
в плоскости VxVy и наоборот. Используя дифференциальное уравнение для характеристик в плоскости
потока, можно записать дифференциальное уравнение
характеристик в плоскости годографа скорости
dVy
dVx
Vx2 a 2
VxVy a Vx2 Vy2 a 2
12

13. 9.1.Течение Прандтля–Майера

Равномерный сверхзвуковой поток газа движется со
скоростью V1 вдоль прямолинейной стенки АО. ОВ и
ОD – линии возмущения (здесь они же – характеристики) – границы области возмущенного движения ВОD,
где происходит непрерывное изменение величины и
направления скорости потока. Найдем параметоы
течения в области ВОD.
13

14.

Введем полярные координаты r и . Составляющие
вектора скорости Vr вдоль характеристики (радиуса r)
и перпендикулярно ему – Vs . Вдоль характеристики,
параметры течения газа неизменны, поэтому
составляющие скорости зависят только от угла .
Движение газа – потенциальное – (r , ).
Исходное уравнение для решения
Vr
Vr ( ),
задачи – уравнение Бернулли:
r
1
Vs
Vs ( ).
s r
2
Vr2 Vs2
a2
Vmax
.
2
k 1
2
Из свойства линии возмущения Vs a. Рассмотрим
0
Vr
Vr
Vs
Vr dVr
dV
rV
V
r
s s
Vs r a
.
Т.к.
и
r
r
r r
d
d
2
то уравнение Бернулли
2
2 dVr
dV
2
V r
V
max ,
d
k
1
d
2
r
14

15.

k 1 dVr
2
2
Vr Vmax . В направлеk 1 d
2
После преобразований
нии течения скорость движения газа возрастает, т. е.
dVr
2
0 . Поэтому dVr k 1 Vmax
Vr2 , после разделения пере
d
d
k 1
менных и интегрирования
Найдем значение постоянной С из граничных условий
на линии возмущения ОВ.
2
V V1
k 1
Vr Vmax sin
C
k 1
k 1
k 1
Vs
Vmax cos
C
k 1
k 1
Vs V1 sin 1 a1
2
1 V1 M1 1
Vr V1 cos 1 V1 1 2
a1 M12 1
V1
M1
a1
Vr
M12 1 с учетом решения
Отношение скоростей
Vs
запишем как
15

16.

1 arctg M12 1,
tg 1 ctg 1 M12 1, то
2
2
k 1
k 1
С
arctg
M12 1 arctg M12 1
Следовательно
k 1
k 1
Так как
При M1 1 постоянная принимает значение С = 0 и
Vr Vmax sin
k 1
k 1
Vs Vmax
k 1
k 1
cos
k 1
k 1
Найдем связь между углом поворота потока и
числом М через отношение скоростей для промежуточной характеристики ОЕ Vr M 2 1 k 1 tg k 1 C
Vs
Отсюда
Т.к.
k 1
k 1
k 1
C
arctg
M 2 1. . Для ОЕ
k 1
k 1
arctg M2 1 , то arctg M 2 1 и
2
k 1
2
16

17.

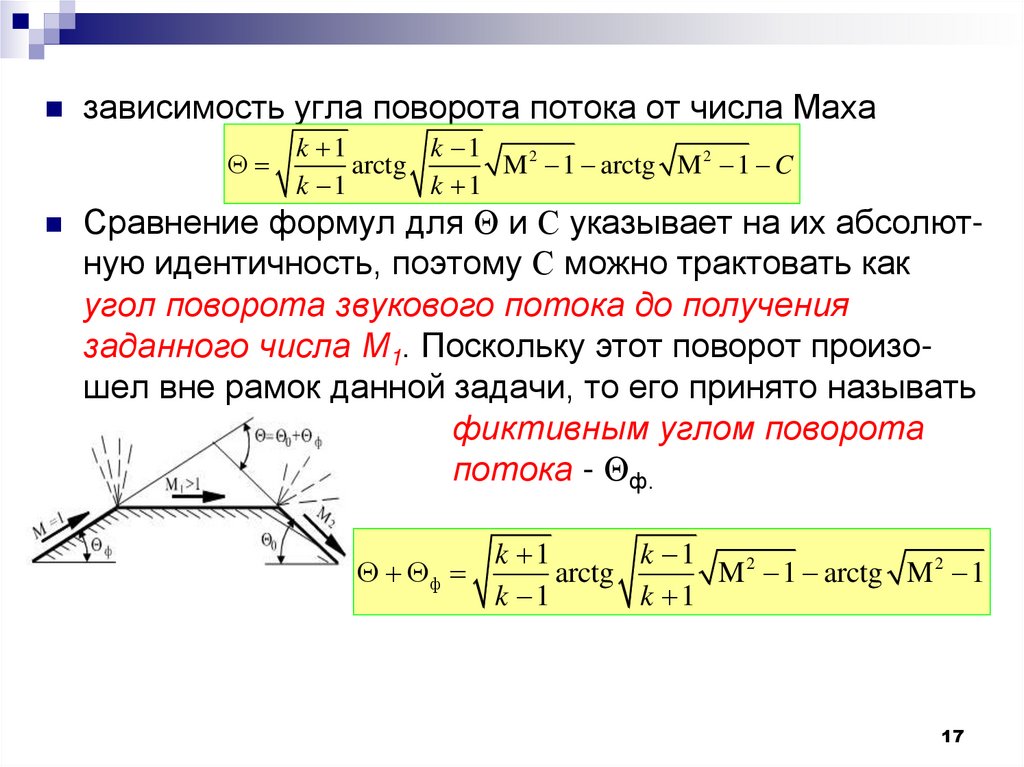
зависимость угла поворота потока от числа Маха
k 1
k 1
arctg
M 2 1 arctg M 2 1 C
k 1
k 1
Сравнение формул для и С указывает на их абсолютную идентичность, поэтому С можно трактовать как
угол поворота звукового потока до получения
заданного числа М1. Поскольку этот поворот произошел вне рамок данной задачи, то его принято называть
фиктивным углом поворота
потока - ф.
ф
k 1
k 1
arctg
M 2 1 arctg M 2 1
k 1
k 1
17

18.

Максимальный угол поворота представляет собой
угол поворота звукового потока ( М = 1, C = 0) до
получения им скорости Vmax (при
k 1
max
1
расширении до абсолютного
2 k 1
вакуума, p = 0 ).
о
Для воздуха (k = 1,4) max 129 30
Предельный угол поворота – это угол, на который
может повернуть сверхзвуковой поток ( М > 1) при
пр max ф
его истечении в вакуум:
Для потока с числом Маха М1 = 1 пр max ,
а для М1 = , пр 0 .
18