Similar presentations:
Аэрогазодинамика. Сверхзвуковые течения со скачками уплотнения (лекции 12, 13)
1. Сверхзвуковые течения со скачками уплотнения
АэрогазодинамикаСверхзвуковые течения со
скачками уплотнения
Лекции 12
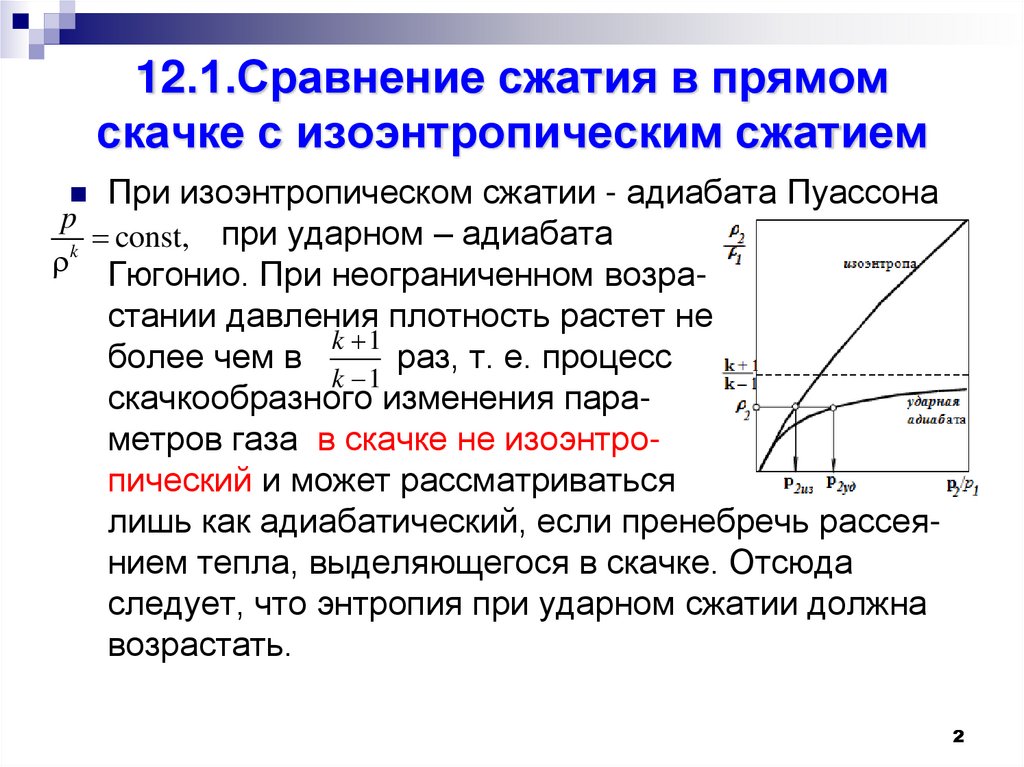
2. 12.1.Сравнение сжатия в прямом скачке с изоэнтропическим сжатием
При изоэнтропическом сжатии - адиабата Пуассонаp
const, при ударном – адиабата
k
Гюгонио. При неограниченном возрастании давления плотность растет не
k 1
более чем в
раз, т. е. процесс
k 1
скачкообразного изменения параметров газа в скачке не изоэнтропический и может рассматриваться
лишь как адиабатический, если пренебречь рассеянием тепла, выделяющегося в скачке. Отсюда
следует, что энтропия при ударном сжатии должна
возрастать.
2
3.
При изоэнтропическом сжатии параметры газа изменяются от p1 , 1 до p2из , 2 . При ударном – от p1 , 1до 2 и p2 p2уд ( p2 p2 из ).
p
S
с
ln
Выражение для энтропии:
V
k
Для изоэнтропического процесса
p2 из
p1
S2 из S1 сV ln k сV ln k
1
2
p2
S2 cV ln k
Для процесса ударного сжатия
2
p2
p2 из
p2
0
Т.к. p2 p2 из , то S2 S1 cV ln k cV ln k cV ln
p2 из
2
2
Таким образом, при ударном сжатии , т. е. при
переходе через фронт скачка уплотнения энтропия
действительно возрастает
Так как при ударном сжатии энтропия увеличивается,
то ударное сжатие – процесс необратимый
3
4.
Т. е. при процессах, происходящих по закону ударнойадиабаты, наблюдается необратимый переход части
механической (кинетической) энергии в тепловую
(температура газа повышается значительно сильнее,
чем при изоэнтропическом сжатии), которая уже не
может быть полностью преобразована обратно в
кинетическую энергию без дополнительных затрат
механической энергии.
Необратимое превращение механической энергии в
тепловую энергию на скачке уплотнения является
источником дополнительного так называемого
волнового сопротивления
4
5. 12.2.Давление в критической точке за прямым скачком уплотнения
Перед затупленным телом образуется отсоединенныйкриволинейный скачок уплотнения. До скачка
параметры потока V1 , p1 , за скачком – V2 , p2 .
В передней критической точке тела
V2 0 и p2 p02 , причем давление p02
не будет равно давлению p01 при
изоэнтропическом торможении газа.
Это в определенной мере препятствует прямому
использованию метода определения скорости потока с
помощью трубки полного напора. Найдем отношение
p
p02 p02 p2
давлений 02 . Запишем его как
p1
p1
p2 p1
5
6.
Т.к. p2 2k M12 k 1p1
k 1
k 1
k 1 2
1
M1
2
2
M2
k 1
kM12
2
После преобразований с учетом
получим формулу Рэлея – формулу
для расчета числа М сверхзвукового потока через
отношение давления торможения за скачком уплотнения к статическому давлению набегающего потока:
2
p02 k 1 k 1
p1 k 1 2 k 1
p02 k 1 2
1
M2
p2
2
k
k 1
При k=1
k
k 1
M12
2k
1
2
k 1 M1
1
k 1
p02
166,7M12
p1 (7 M1 2 )2,5
6
7. 12.3.Зонды для измерения статического давления
Для измерения статического давления всверхзвуковом потоке
применяются специальные зонды, позволяющие измерять статическое давление не за скачком уплотнения, а за
волнами возмущения. Изменения давления в этом
случае настолько малы, что ими можно пренебречь.
Измерив давление торможения за скачком уплотнения
и статическое давление в набегающем потоке, можно
при помощи формулы Рэлея рассчитать число Маха
набегающего потока
7
8. 12.4.Коэффициент восстановления полного давления
p02p01
Зависимости
для ударного и
для изоэнтроp1
p1
пического торможения от числа М показывают, что при течении со скачком уплотнения наблюдаются потери полного давления (потери напора), т. е. необратимые
потери механической энергии. Потери
механической энергии характеризует
коэффициент потерь полного напора (коэффициент
восстановления полного давления)
p02
166,7M12
σ
при k = 1,4
σ
2 2,5
2 3,5
p01
(7 M ) 1 0,2M
1
1
8
9.
Зависимость коэффициентавосстановления полного давления
от числа Маха указывает на
существенный рост потерь полного
напора при увеличении числа Маха
При переходе через скачок уплотнения температура
торможения T0 не изменяется, поэтому из уравнения
состояния следует, что плотность заторможенного
потока при переходе через скачок уплотнения
уменьшается пропорционально полному давлению,
т. е. 02 / 01 p02 / p01 .
Зависимость σ σ(M) показывает, что при числах
1 M1 1,5 коэффициент мало отличается от
единицы как для прямых, так и для косых скачков
уплотнения.
9
10.
Это обстоятельство используют для торможениясверхзвукового потока до дозвуковой скорости с
наименьшими потерями механической энергии в
системе скачков уплотнения.
Коэффициент для системы скачков уплотнения,
состоящей из косых скачков и одного прямого, может
быть найден как
p
p p
p
σ
0n
p01
02
03
p01 p02
0n
p0(n 1)
σ1 σ2
σ n 1
скачков будет максимальным тогда,
когда интенсивности скачков, характеризуемые
величинами M i sin i , будут одинаковыми. Такую
систему косых скачков уплотнения называют
оптимальной.
Для системы
10
11. 13.1.Связь между углом поворота потока и углом наклона косого скачка уплотнения
13.1.Связь между углом поворотапотока и углом наклона косого скачка
Фронт
уплотнения
V2 n
tg
V
скачка
Из рисунка следует
Из формулы Прандтля для косого
скачка
Т.к.
V2 n
V1n V1 sin
1 2 k 1 2
V
aкр
V1n
k 1
V V1 cos , то
2
aкр
k 1 2
M1 cos 2
2
a
k 1
tg 1 2
M1 sin cos
k 1 2
V1 cos 2
k 1
или
tg
2
V1 sin cos
2
aкр
Tкр Tкр T0
2 k 1 2
2
Т.к. a kRT
M1 , тогда
1
2
a1
T1 T0 T1 k 1
2
2 k 1 M12 sin 2 . Поскольку tg tg tg
tg
1 tg tg
k 1 M12 sin cos
2
aкр
11
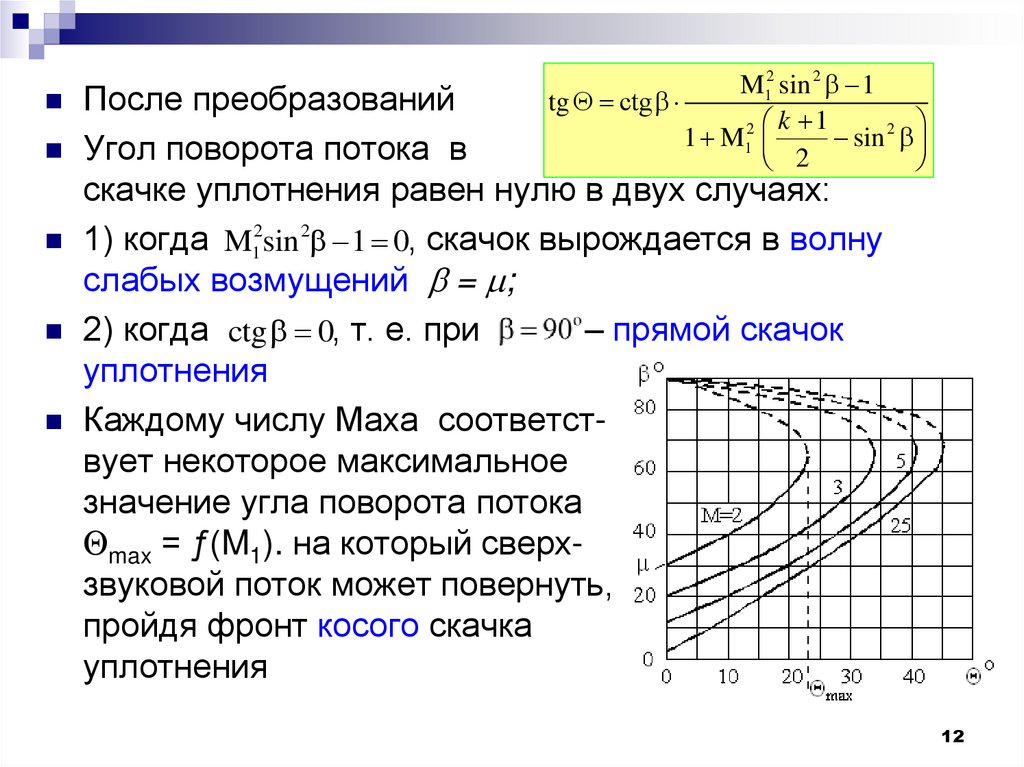
12.
M12 sin 2 1tg сtg
k 1
1 M12
sin 2
2
После преобразований
Угол поворота потока в
скачке уплотнения равен нулю в двух случаях:
2
2
1) когда M1 sin 1 0, скачок вырождается в волну
слабых возмущений = ;
2) когда ctg 0, т. е. при
– прямой скачок
уплотнения
Каждому числу Маха соответствует некоторое максимальное
значение угла поворота потока
max = ƒ(M1). на который сверхзвуковой поток может повернуть,
пройдя фронт косого скачка
уплотнения
12
13.
При данном М1 одному и тому же значению соответствуют два значения , соответствующих сильным(штриховая часть линий) и слабым (сплошная часть
кривых) скачкам уплотнения.
Если угол клина кл max , то возникает
присоединенный (сравнительно слабый)
косой скачок уплотнения. Угол поворота
потока в таком скачке равен кл. Угол
Косой присоединенный –
слабый скачок
наклона скачка определяется по
сплошным кривым.
Если кл max , то образуется
отсоединенный криволинейный скачок
уплотнения. Ему отвечает целиком вся
линия графика зависимости от .
Криволинейный отсоединенный
- сильный скачок
13
14. 13.2.Ударная поляра
Найдем уравнение годографаскорости в виде V2 y f V2 x ,V1 .
В соответствии с рисунком можем
записать выражения
V2 x V cos V2 n sin ,
V2 y V sin V2 n cos .
2
Т.к. V1nV2 n aкр
k 1 2
V ,
k 1
первого уравнения системы
получаем
и V V1 cos , то из
2
2
V
cos
2
y
ctg 2
1 cos 2 V1 V2 x 2
Из АВС:
откуда cos
2
V22y
V1 V2 x V
2
2
2y
и
14
15.
2aкр
V2 x
V1
V22y (V1 V2 x ) 2
2
aкр
2
V1
V2 x
k 1
V1
Из формулы следует, что годограф
скорости за скачком уплотнения есть
кривая, симметричная относительно
оси абсцисс, с вертикальной асимптотой . Кривая пересекает ось
абсцисс ( V2 y 0 )при значениях V2 x :
V1 V2 V2 х скачок уплотнения вырождается в волну слабых возмущений (точка
В);
2
aкр
V2 х V2
- прямой скачок уплотV1
нения (точка А).
15
16.
Петлю этой кривой называют ударной полярой.Бесконечные ветви физического смысла не имеют, так
как для них V2 V1, что возможно только в скачке
разрежения, который для адиабатического течения
невозможен (например, точка 3).
При max образуется отсоединенный криволинейный (сильный) скачок уплотнения, угол наклона
которого, при переходе от центральной линии тока к
o
периферии течения, изменяется в пределах 90 .
В центральной части скорость течения за
криволинейным скачком дозвуковая
16














 physics
physics








