Аэрогазодинамика. Одномерные изоэнтропические течения газа (лекция 6)

1. Одномерные изоэнтропические течения газа

Аэрогазодинамика
Одномерные изоэнтропические
течения газа
Лекция 6
1

2.

Сжатие (расширение) газа сопровождается
повышением (понижением) давления - газ обладает
свойствами упругого тела. Местное уплотнение
малой интенсивности ( / 1 , p / p 1 ) будет
распространяться в виде волны возмущения с
некоторой скоростью . Такую же природу имеет
звуковая волна, представляющая собой продольные
волны малой интенсивности.
Поэтому скорость распространения любых малых
возмущений в газе равна скорости звука.
2

3. 6.1. РАСПРОСТРАНЕНИЕ МАЛЫХ ВОЗМУЩЕНИЙ. СКОРОСТЬ ЗВУКА

Если газ покоится (V 0 ), то возмущения в моменты
времени t1 , t2 , t3 и т. д. образуют ряд концентрических сферических волн с центрами в точке О и
радиусом от нуля до аti на рассматриваемом отрезке
времени.
При движении точечного источника
возмущений с дозвуковой скоростью V < а
сферические волны смещаются в сторону
движения источника, но опережают его, т.е.
источник находится внутри вызванной им
сферической волны.
При звуковой скорости источника передний край
волны возмущения и положение источника совпадают
3

4.

Когда скорость источника возмущений становится
больше скорости распространения волн (V > a), тело
обгоняет волны, оставляя их позади себя в виде
расширяющегося конуса, вершиной которого
является само тело. Возмущения при сверхзвуковых
скоростях навстречу потоку не распространяются,
т.е. не проникают вперед в невозмущенную область.
Этот конус является огибающей
сферических волн возмущений и
называется конусом возмущения,
или конусом Маха.
На плоскости, проходящей через ось конуса,
получаем прямые OB и OB1, называемые линиями
слабых возмущений (линиями Маха) - ударные
волны бесконечно малой интенсивности.
4

5.

Угол , равный половине угла
1
at a
при вершине конуса, называют sin , sin
Vt V
M
углом возмущений
При увеличении числа М угол уменьшается, т. е.
зона возмущений сужается (М , 0).
dp
2
a .
Скорость звука определяется как
d
Т.е. скорость звука зависит от закона, связывающего
изменение давления с изменением плотности.
p
Для изоэнтропического процесса
a k kRT
Для воздуха k = 1,4, R=287 Дж/кг/К
a 20,1 T (м/с)
5

6. 6.2.СООТНОШЕНИЯ ДЛЯ ОДНОМЕРНЫХ ИЗОЭНТРОПИЧЕСКИХ ПОТОКОВ ГАЗА

Изоэнтропическое течение газа вдоль трубки тока.
Уравнение Бернулли
V02
V2
i0
i
2
2 2
k
k
V
RT0
RT
или
k 1
k 1
2
при V0 0
V2
i0 i
2
Параметры газа, соответствующие сос-
тоянию покоя, называются параметрами изоэнтропически заторможенного
потока или параметрами торможения.
Давление p0 , называют еще полным давлением.
При торможении газа происходит повышение темпера
туры, равное
k 1V 2
V2
T T0 T
; для воздуха T
2009
2k R
6

7.

Все теплосодержание i0 переходит в кинетическую
2
энергию Vmax
/ 2 при расширении газа до абсолютного
вакуума ( p 0 ) – поток достигает теоретической
максимальной скорости течения газа Vmax 2i0
Vmax 2i0
2k
2k p0
2
RT0
a0
k 1
k 1 0
k 1
Т.к. при изоэнтропическом течении идеального1 газа
1
k
0 p0 и p 0 T , то
p0 T0
p
p T
p0 T0
k
k 1
и
T k 1
0 T0
Формулы для расчета p, , T при изоэнтропическом
1
k
течении газа:
2
T
V
1 2
T0
Vmax
V 2 k 1
1 2
0 Vmax
p
V 2 k 1
1 2 ;
p0 Vmax
7

8.

При изоэнтропическом течении газа увеличение его
кинетической энергии может происходить только при
понижении теплосодержания (потенциальной
энергии), при этом p, , T - уменьшаются
При изоэнтропическом (или адиабатическом)
течении газа с ростом скорости происходит
расширение газа
2
2
a2 V 2
T a
V
2 1
2 1 2 , то можно записать
Т.к.
2
T0
a0
Vmax
Местная скорость потока, равная
местной скорости звука, называется критической V a aкр
Сечение струи газа, в котором
достигается это условие, называют критическим
a0
Vmax
Изоэнтропический эллипс
8

9.

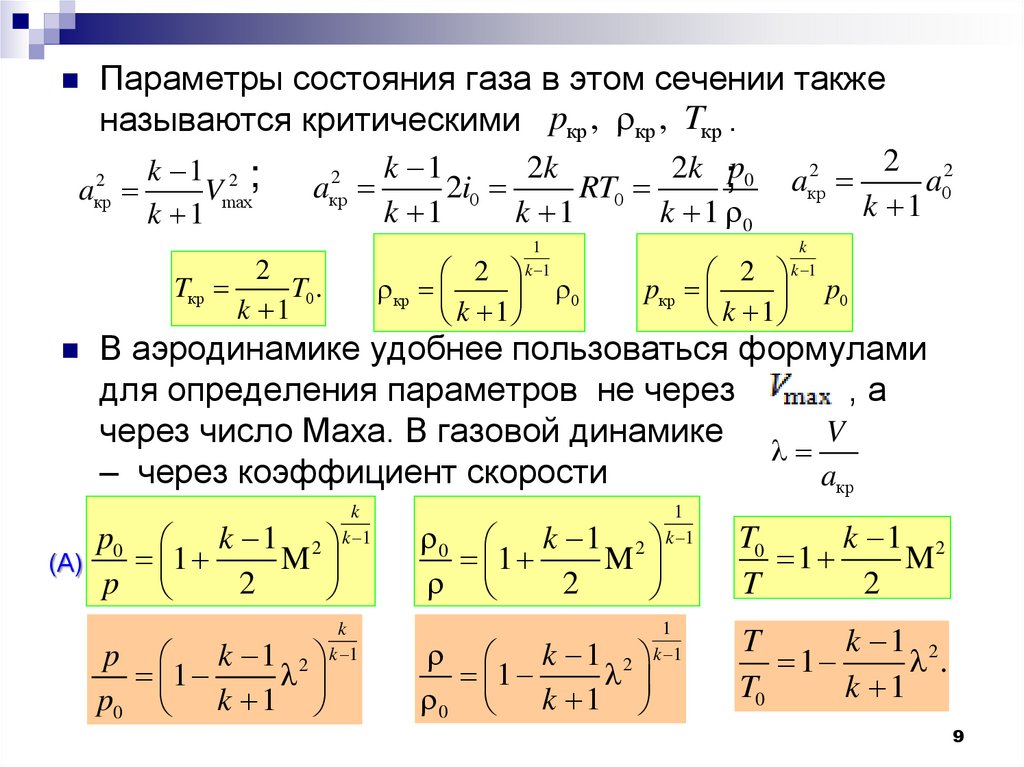
Параметры состояния газа в этом сечении также
называются критическими pкр , кр , Tкр .
k 1 2 ;
a
Vmax
k 1
2
кр
Tкр
k 1
2k
2k ;p0
a
2i0
RT0
k 1
k 1
k 1 0
2
кр
2
кр
k
1
2
T0 .
k 1
1
k 1
0
2
pкр
k
1
2
aкр
k
k 1
2 2
a0
k 1
p0
В аэродинамике удобнее пользоваться формулами
для определения параметров не через
,а
V
через число Маха. В газовой динамике
– через коэффициент скорости
aкр
p0 k 1 2
1
M
(А)
p
2
p k 1 2
1
p0 k 1
k
k 1
k
k 1
0 k 1 2
1
M
2
k 1 2
1
0 k 1
1
k 1
1
k 1
T0
k 1 2
1
M
T
2
T
k 1 2
1
.
T0
k 1
9

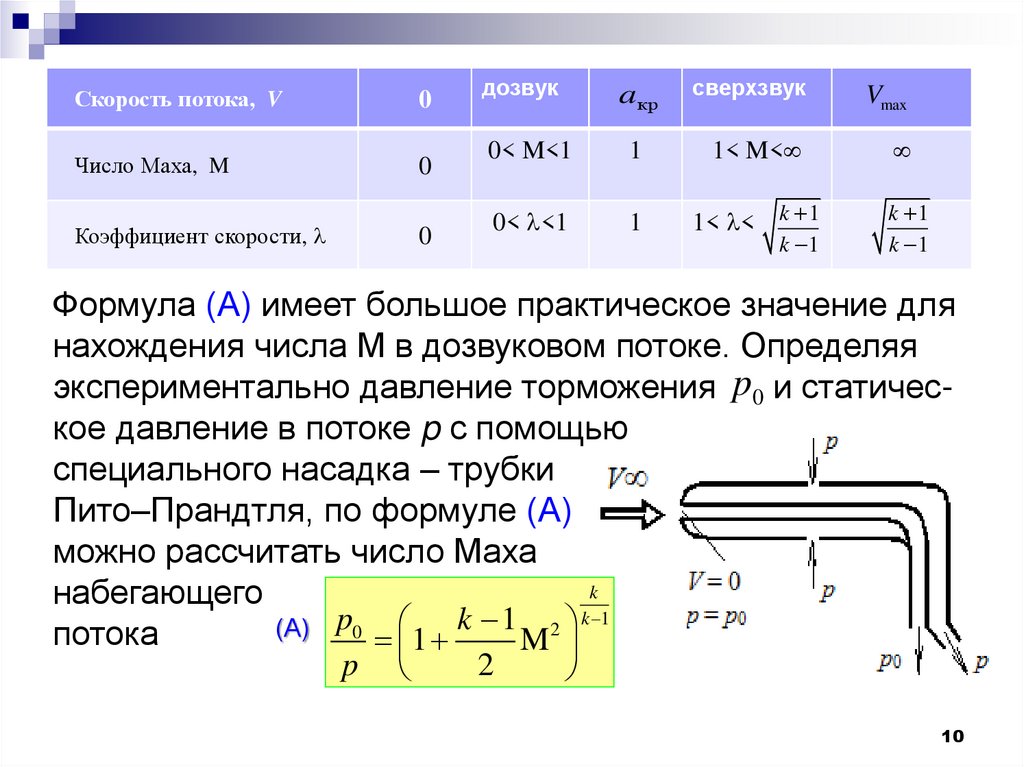
10.

Скорость потока, V
0
Число Маха, M
0
Коэффициент скорости,
0
дозвук
aкр
сверхзвук
Vmax
0< M<1
1
1< M<
0< <1
1
1< < k 1
k 1
k 1
k 1
Формула (А) имеет большое практическое значение для
нахождения числа М в дозвуковом потоке. Определяя
экспериментально давление торможения p0 и статическое давление в потоке p с помощью
специального насадка – трубки
Пито–Прандтля, по формуле (А)
можно рассчитать число Маха
k
набегающего
k 1
p
k
1
2
(А)
0
потока
1
M
p
2
10

11. 7.1.СВЯЗЬ МЕЖДУ СКОРОСТЬЮ ТЕЧЕНИЯ ГАЗА И ФОРМОЙ ЕГО СТРУИ

Уравнение неразрывности для установившегося
движения идеальной жидкости в трубке тока в форме
массового расхода VF const после d dV dF 0
V
F
дифференцирования примет вид
2
d
V
dV
Из уравнения Бернулли и формулы
2
a V
для скорости звука
V 2 dV
dF
dF
2 dV
1
(1 M )
Следовательно
или
2
F
a
V
F
V
2
1. Если V < а, т. е. 1 M 0 , то dF ̶ dV. В дозвуковом
потоке скорость газа меняется так же, как и в потоке
несжимаемой жидкости: с увеличением площади поперечного сечения F скорость V убывает и наоборот
11

12.

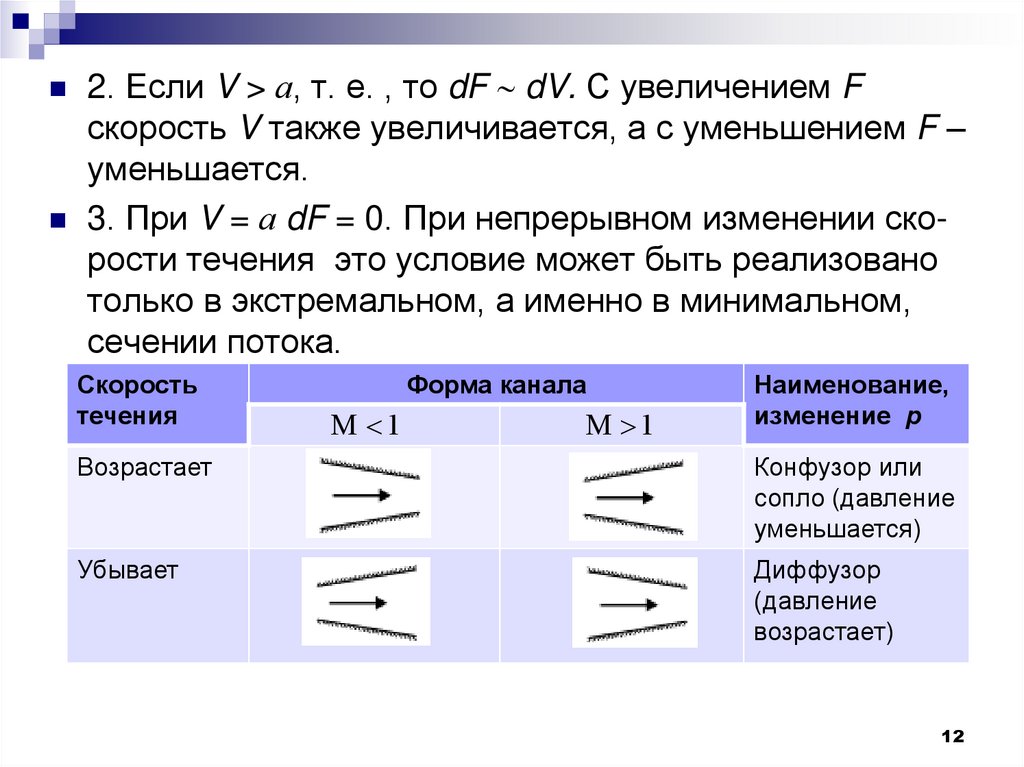
2. Если V > а, т. е. , то dF dV. С увеличением F
скорость V также увеличивается, а с уменьшением F –
уменьшается.
3. При V = а dF = 0. При непрерывном изменении скорости течения это условие может быть реализовано
только в экстремальном, а именно в минимальном,
сечении потока.
Скорость
течения
Форма канала
M 1
M 1
Наименование,
изменение р
Возрастает
Конфузор или
сопло (давление
уменьшается)
Убывает
Диффузор
(давление
возрастает)
12

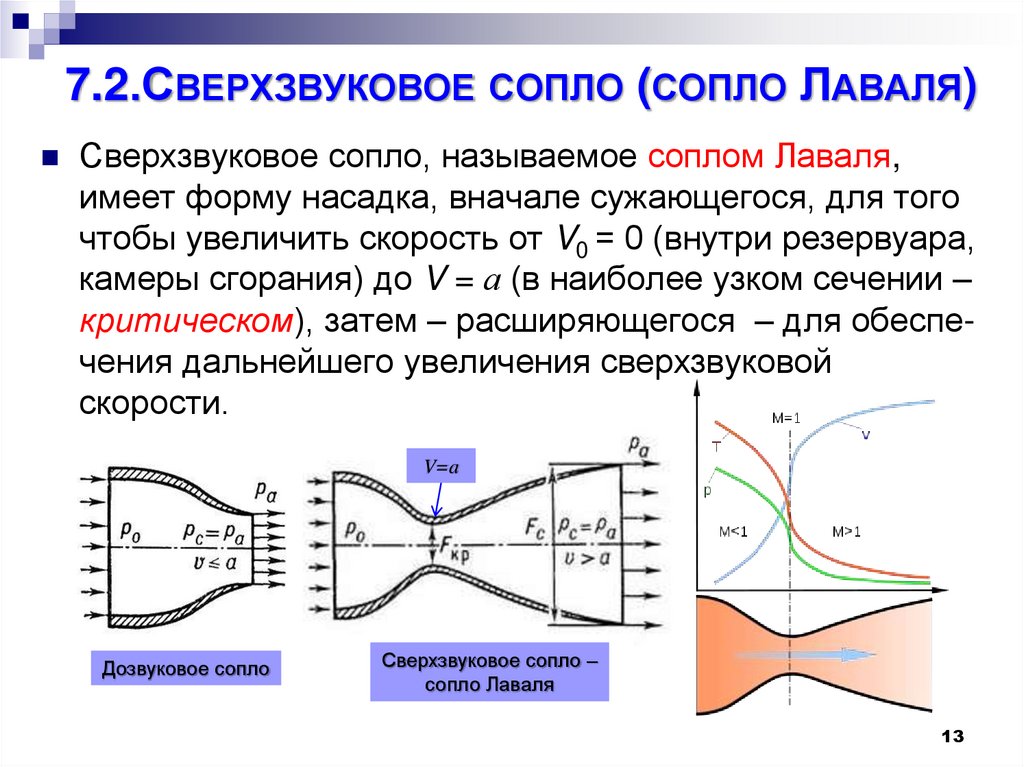
13. 7.2.СВЕРХЗВУКОВОЕ СОПЛО (СОПЛО ЛАВАЛЯ)

Сверхзвуковое сопло, называемое соплом Лаваля,
имеет форму насадка, вначале сужающегося, для того
чтобы увеличить скорость от V0 = 0 (внутри резервуара,
камеры сгорания) до V = а (в наиболее узком сечении –
критическом), затем – расширяющегося – для обеспечения дальнейшего увеличения сверхзвуковой
скорости.
V=a
Дозвуковое сопло
Сверхзвуковое сопло –
сопло Лаваля
13

14.

Т.к. площадь поперечного сечения струи связана со
скоростью течения газа, то зависимость отношения
k 1
площадей от числа Маха для
2( k 1)
Fкр
k
1
сопла Лаваля показывает, что
M
2
F
2
(
k
1)
M
при изоэнтропическом течении
газа число Маха, которое необходимо получить в
данном сечении, зависит только от отношения
площадей и физических свойств газа (строения его
молекулы).
Таким образом можно найти число Маха в любом
сечении сопла. Затем при помощи газодинамических
функций и соответствующих параметров торможения
можно рассчитать p, , T , а также величину скорости
течения в этом сечении (в т.ч. и на срезе сопла).
14

15. 7.3.РЕЖИМЫ РАБОТЫ СВЕРХЗВУКОВОГО СОПЛА

Характер распределения параметров течения газа в
сопле зависит от степени нерасчетности струи n,
равной отношению давления на выходе из сопла pa к
давлению окружающей среды pн ( n pa / pн ). В
зависимости от величины нерасчетности n сопло
может работать в следующих режимах: расчетном,
недорасширения и перерасширения.
Расчетный режим – давление на срезе сопла равно
давлению окружающей среды: pa pн (n 1) .
Режим недорасширения – давление на срезе сопла
больше давления окружающей среды: pa pн ( n 1).
Характер изменения скорости и давления газа в
тракте сопла на этом режиме совпадает с расчетным.
15

16.

Режим перерасширения –
давление на срезе сопла меньше давления окружающей
среды: pa pн (n 1). До некоторого предела повышение pн не
влияет на течение по соплу,
которое остается расчетным.
Такое истечение возможно лишь
при pн 2,5 pa ( 0,4 n 1) перерасширение без отрыва
потока от стенок сопла.
При значительном противодавлении среды (n 0,4) поток
отрывается от стенок сопла. Место отрыва приближается
к критическому сечению по мере уменьшения степени
нерасчетности – перерасширение с отрывом потока.
16

17. 7.4.Истечение из сопла на режиме перерасширения

без отрыва потока от стенок сопла
с отрывом потока от стенок сопла
17