Аэрогазодинамика. Тела вращения в сверхзвуковом потоке (лекции 22, 23)

1.

Аэрогазодинамика
Тела вращения в
сверхзвуковом потоке
Лекции 22, 23
1

2. 22.1.Конический и осесимметричный потоки

Коническим называют поток, в котором параметры
газа на конической поверхности сохраняются
постоянными. Они изменяются только при переходе
с одной конической поверхности на другую.
Осесимметричным называют течение, обладающее
симметрией относительно оси тела (т.е само тело
также обладает осевой симметрией). В этом случае
течение газа во всех меридиональных плоскостях
одинаково, и движение газа можно изучать как
плоское в одной из меридиональных плоскостей
2

3. 22.2.Осесимметричное обтекание острого конуса

Результаты решения задачи осесимметричного ( 0 )
обтекания острого конуса используются в следующих
случаях:
а) для определения коэффициента волнового
сопротивления конических головных частей корпусов
ЛА;
б) в качестве исходных данных для численного
расчета обтекания конусов при 0 ;
в) в качестве начальной точки при расчете обтекания
тел с криволинейной образующей;
г) для приближенного расчета распределения
давления по поверхности тел более сложной формы
3

4.

При симметричном обтекании конуса с углом полураствора к( к max при заданном числе Маха) перед
ним возникает присоединенный конический
скачок уплотнения с вершиной
в вершине конуса.
Задача расчета обтекания конуса
сводится к нахождению угла полураствора
конического скачка и поля скоростей
(и давлений) между скачком уплотнения
Осесимметричное
обтекание острого конуса
и конусом.
Для всех плоскостей, перпендикулярных продольной
оси конуса, граничные условия одинаковы и течения
между конусом и скачком уплотнения геометрически
подобны. В сходственных точках этих сечений (на
конических поверхностях) параметры потока
одинаковы – коническое течение
4

5.

Задача решается в полярной системе координат (r , )
Vr Vr ( ), V V ( )
с полюсом в вершине конуса:
Течение между конусом и скачком является
изоэнтропическим и потенциальным (безвихревым).
1
Следовательно r , и Vr
, V
r
r
Для осесимметричного конического потока потенциал
скорости r , r F . Тогда
Vr
F
r
V
1
F
r
V
dVr
d
Из уравнения неразрывности div V 0 (для осесимметричного установившегося течения - в сферических
координатах): div V d V d 2 Vr V ctg 0,
после преобразований V 2 dV V 2
2 2 Vr V ctg 0
1 2
получаем:
a d
a
5

6.

В итоге получаем систему двух уравнений для расчета
Vr и V :
2
2
Vr
a
V
2
ctg
V
dV
;
2
2
1 V a
d
dVr
V .
d
Граничные условия:
1) на поверхности конуса нормальная составляющая
вектора скорости равна V к 0 (из условия
непротекания), тогда касательная составляющая
скорости направлена по касательной к поверхности
конуса и равна скорости на его поверхности:
Vr ( к ) Vк
6

7.

2) на поверхности скачка уплотнения составляющие
скорости Vr и V должны удовлетворять основным
соотношениям для косого скачка уплотнения:
а) касательная составляющая скорости при переходе
через скачок уплотнения не изменяется:
Vr V V cos ;
б) нормальная составляющая V (она же V2n) должна
удовлетворять формуле Прандтля для косого скачка
уплотнения:
k 1 2
2
V V sin aкр
V cos 2
k 1
Система дифференциальных уравнений при данных
граничных условиях решается методом численного
интегрирования – методом конечных разностей.
Интегрирование можно начать как с поверхности
конуса, задаваясь значением Vк и к , так и с
поверхности скачка, задаваясь углом и числом
Маха M (скоростью V ).
7

8. Численное интегрирование системы

Систему дифференциальных уравнений приводят к
безразмерному виду и представляют в виде уравнений
в конечных разностях
V ctg 2 V 2 a 2 Vr
V n 1 V n
,
2
2
1 V a
n
Vr n 1 Vr n V n .
(А)
Зададимся углом полураствора конуса к и скоростью Vк
на его поверхности. Зададимся приращением , т.е.
0, 0 0
к
шагом интегрирования. На нулевом шагеn( n 0,
)к
имеем следующее: V 0 и Vr Vк .
Первый шаг: 1 к . Из первого уравнения системы (А) получаем V 1 2Vк . Из второго уравнения
найдем Vr 1 на промежуточном конусе с углом 1 и
т.д.
8

9.

Интегрирование проводим до тех пор, пока не будет
выполняться условие (б) на поверхности скачка,
также приведенное к безразмерному виду.
Рассчитываем число M , соответствующее заданной
скорости на поверхности конуса, затем - параметры
p2 , 2 , T2 за скачком уплотнения и параметры поля
течения между скачком и конусом, используя
формулы изоэнтропического течения.
9

10. 22.3. Волновое сопротивление изолированного конуса

Сила лобового сопротивления, действующая на
конус, равна X pк sin к Sбок p Sдн pк p Sдн ,
p
так как Sбок sin к Sдн .
Поскольку повышенное давление на
p
поверхности конуса создается за счет
S
S
потерь части механической энергии
сверхзвукового потока в скачке уплотК расчету волнового
сопротивления
конуса
нения, то возникающее за счет этого
сопротивление называют волновым. Тогда
коэффициент сопротивления, он же коэффициент
pк p Sдн
X
волнового сопротивления,
cх в
pк
k
равен
Sдн q
S
p M2
к
к
д
н
бо
к
дн
2
10

11.

То есть, коэффициент волнового сопротивления
изолированного конуса численно равен коэффициенту
давления на его поверхности pк .
Коэффициент давления на поверхности конуса
рассчитывается по общему выражению
2 1 pк
pк
1
для коэффициента давления:
2
k M p
Скорость потока на поверхности конуса меньше, чем
за скачком уплотнения, а угол поворота потока при
переходе через конический скачок уплотнения меньше
угла конуса (< к). Угол наклона вектора скорости при
перемещении от скачка к конусу увеличивается до к.
Поэтому линии тока в возмущенной области (в отличие
от клина) являются криволинейными
11

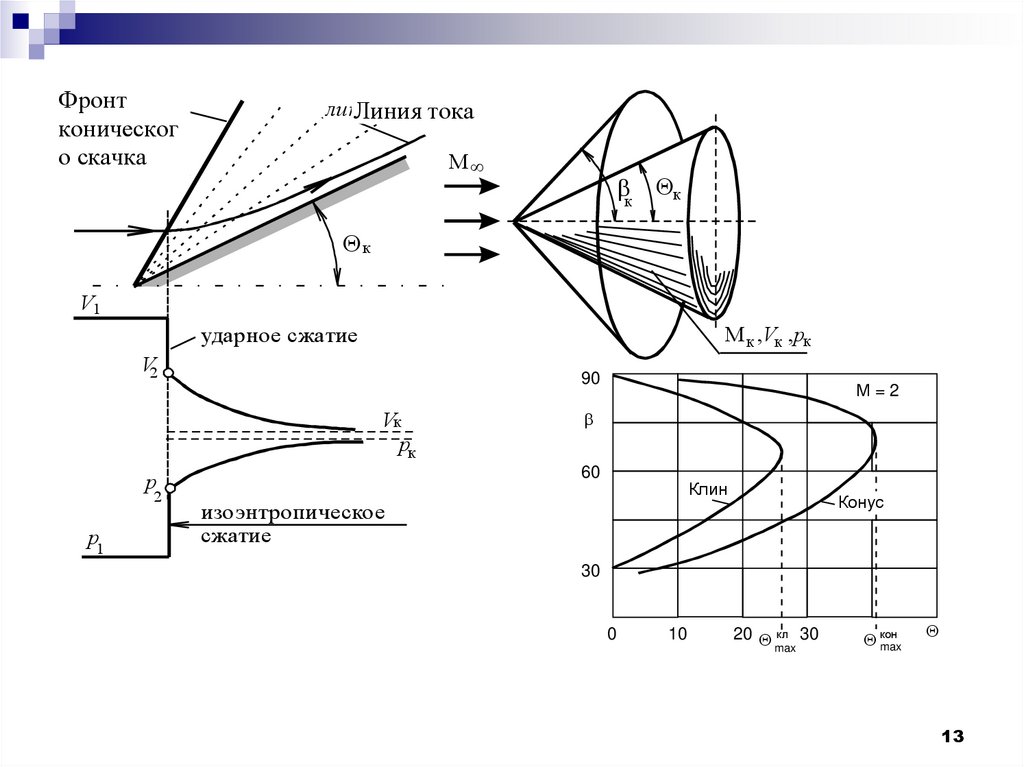
12. 22.4. Отличия обтекания конуса и клина сверхзвуковым потоком

Угол наклона конического скачка уплотнения меньше
угла наклона плоского косого скачка уплотнения, а
максимальный угол поворота потока, до которого скачок
остается присоединенным к телу, для конуса больше,
чем для клина.
Скорость течения вдоль линий тока уменьшается, а
давление возрастает. Следовательно, при обтекании
конуса поток испытывает сначала ударное сжатие на
скачке уплотнения, а затем изоэнтропическое сжатие в
области между скачком и поверхностью конуса.
Поэтому волновое сопротивление конуса при прочих
равных условиях меньше, чем для идентичного клина.
12

13.

Фронт
Фронт
конического
коническог
оскачка
скачка
упплотнения
уплотнения
линия
тока
Линия
тока
M
к
к
к
V1
M к ,Vк ,pк
ударное сжатие
V2
90
Vк
pк
p1
60
p
2
М=2
Клин
Конус
изоэнтропическое
сжатие
30
0
10
20 кл 30
max
кон
max
13

14. 23.1. Несимметричное обтекание конуса

При сверхзвуковом обтекании конуса под углом атаки
поток около него будет обладать свойством конического течения с той особенностью, что параметры
остаются постоянными не целиком на конической
поверхности, а вдоль отдельных прямолинейных
образующих конуса. Параметры газа в таком потоке
изменяются при переходе от одной образующей,
проходящей через вершину конуса, к другой.
В сферической системе координат уравнение конуса,
наклоненного к оси потока под углом атаки имеет вид:
1
к cos 2 ctg к sin 2
2
Для подветренной образующей 0 , а для
наветренной – .
14

15.

Из свойств конического потока следует, что значения
его параметров не зависят от r, а являются функциями
переменных и . Несимметричный конический
сверхзвуковой поток в плоскости = const за скачком
будет изоэнтропическим. Это объясняется тем, что
фронт скачка в этой плоскости представляет собой
прямую линию и энтропия за скачком будет постоянной,
так как условия перехода газа через скачок одинаковы
для каждой линии тока. Это же будет наблюдаться в
любой другой плоскости. Но т.к. угол наклона скачка
неодинаков в каждой из этих плоскостей, неодинаковой
будет и энтропия, являющаяся, таким образом,
функцией угла . Следовательно, в целом
несимметричный конический поток за скачком
оказывается неизоэнтропическим.
15

16.

Теоретической основой для исследования такого
потока являются уравнения движения идеальной
среды и уравнение неразрывности в сферической
системе координат. Решения системы
дифференциальных уравнений находят в виде
Vr V ( ) U ( ) cos (nx) +...,
n =0
..........................................................
0
r
Здесь параметры с верхним индексом «0» относятся к
параметрам симметричного обтекания на конусе с
углом . При малых углах атаки значения параметров
будут мало отличаться от соответствующих значений
при симметричном обтекании, и его влияние
достаточно учесть только линейными членами (n = 1).
16

17.

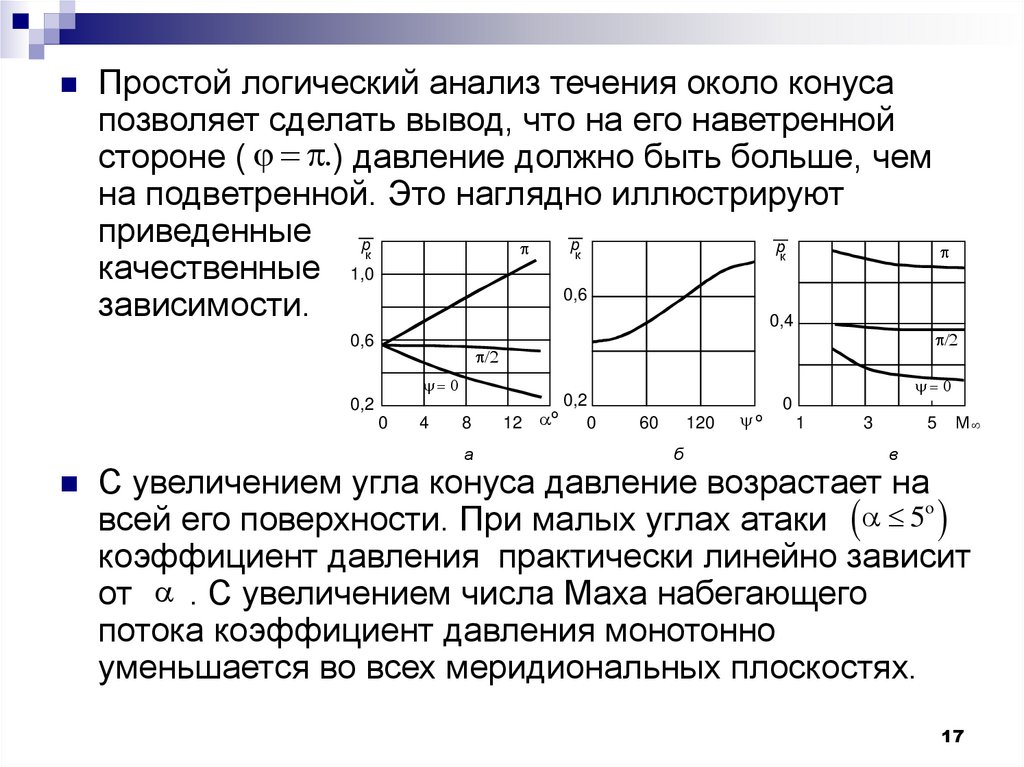
Простой логический анализ течения около конуса
позволяет сделать вывод, что на его наветренной
стороне ( .) давление должно быть больше, чем
на подветренной. Это наглядно иллюстрируют
приведенные р
р
р
качественные 1,0
0,6
зависимости.
0,4
к
к
0,6
/2
/2
y 0
0,2
0
4
8
а
к
12
0,2
о
0
y 0
60
120
б
yо
0
1
3
5
М
в
С увеличением угла конуса давление возрастает на
всей его поверхности. При малых углах атаки 5o
коэффициент давления практически линейно зависит
от . С увеличением числа Маха набегающего
потока коэффициент давления монотонно
уменьшается во всех меридиональных плоскостях.
17

18. 23.2. Приближенный метод расчета

Для приближенного расчета давления и коэффициента
волнового сопротивления заостренных тел вращения
произвольной формы применяется метод
касательных (местных) конусов.
r
0 r
В случае аналитического задания
x
формы тела определение угла
R
местного конуса выполняется
Построение касательного конуса
для тела вращения
достаточно просто. Так для головной
R rм r
cos
части оживальной формы
R
Т.е. производят замену плавной образующей тела
вращения на ломаную линию (исходное тело с
криволинейной образующей заменяют составным
коническим).
м
x
18

19.

Аналогично, для оценки параметров на поверхности
конуса при 0 можно воспользоваться результатами,
полученными для 0.
При несимметричном обтекании
Ось
местных
конуса считаем, что каждая обра- M
конусов
зующая конуса, отклоненного на
угол , принадлежит условному
конусу с углом м (местный угол),
Построение местных конусов
для подветренной и наветренной
симметрично обтекаемому потоком
образующих конуса
Имея результаты теории симметричного обтекания,
можно определить параметры на той образующей,
которая принадлежит этому «местному» конусу. Таким
образом, основным элементом расчета является угол
«местного конуса»:
1 2
2
п
м
к
н
м
Θ м Θ к cosψ ctgΘ к sin ψ
2
19