Similar presentations:
Electronic, Vibrational and Thermal Properties of α and β Titanium
1.
Institute of Strength Physics and Materials Science SB RAS (Tomsk, Russia)National Research Tomsk State University (Tomsk, Russia)
Electronic, Vibrational and Thermal
Properties of α and β Titanium
Prepared by 2nd year graduate student Kasparyan S.O.
Scientific supervisor, Doctor of phys.-math sciences, professor S.E. Kulkova
Scientific consultant Ph.D of phys.-math sciences A.V. Bakulin
2.
IntroductionTitanium and alloys based on it are widely used for various technological
applications in the aerospace, automotive, and shipbuilding industries, since they have
a good strength-to-weight ratio, and also have a good combination of mechanical
properties. To understand the fundamental properties of titanium, as well as phase
transformations, it is necessary to study the electronic and phonon structure of its main
phases. The atomic and electron structures of α and β of titanium are calculated by the
method of projection coupled waves within the framework of the theory of the electron
density functional. In order to understand the fundamental properties of titanium, as
well as phase transformations, it is necessary to study the electronic and phonon
structure of its main phase method of projection coupled waves in the framework of the
theory of the electron density functional, the atomic and electron structures of α and β
of titanium are calculated.
Key words: titanium phase stability, electronic structure, phonon subsystem,
thermodynamic characteristics, ab-initio calculations
3.
MethodTo describe the α phase, a hexagonal cell containing two titanium atoms with
coordinates (1/3,2/3,1/4) and (2/3,1/3,3/4) was used, and calculations of the total energy were
carried out using a G-centered grid of k-points 15×15×9.
The β-phase simulation was carried out using a volume-centered cell and a
15×15×15 grid of k-points generated according to the Monkhorst-Pack scheme. In the
framework of the harmonic approximation, the finite displacement method was used to
calculate the phonon spectrum (the dependence of the oscillation frequency ω(q, s) on the
wave vector q and the type of phonon s).
and
4.
These functions allow us to estimate the lattice heat capacity at a constant volumeand vibrational free energy
The lattice heat capacity at constant pressure was also evaluated for comparison with the
experiment:
where αV is the volumetric coefficient of thermal expansion, B is the volumetric modulus
of elasticity, V is the volume, T is the temperature. The vibrational entropy was calculated
using the following formula:
The coefficient of electronic specific heat was estimated as
where kB is the Boltzmann constant, N(EF) is the density of electronic states at the Fermi
level.
5.
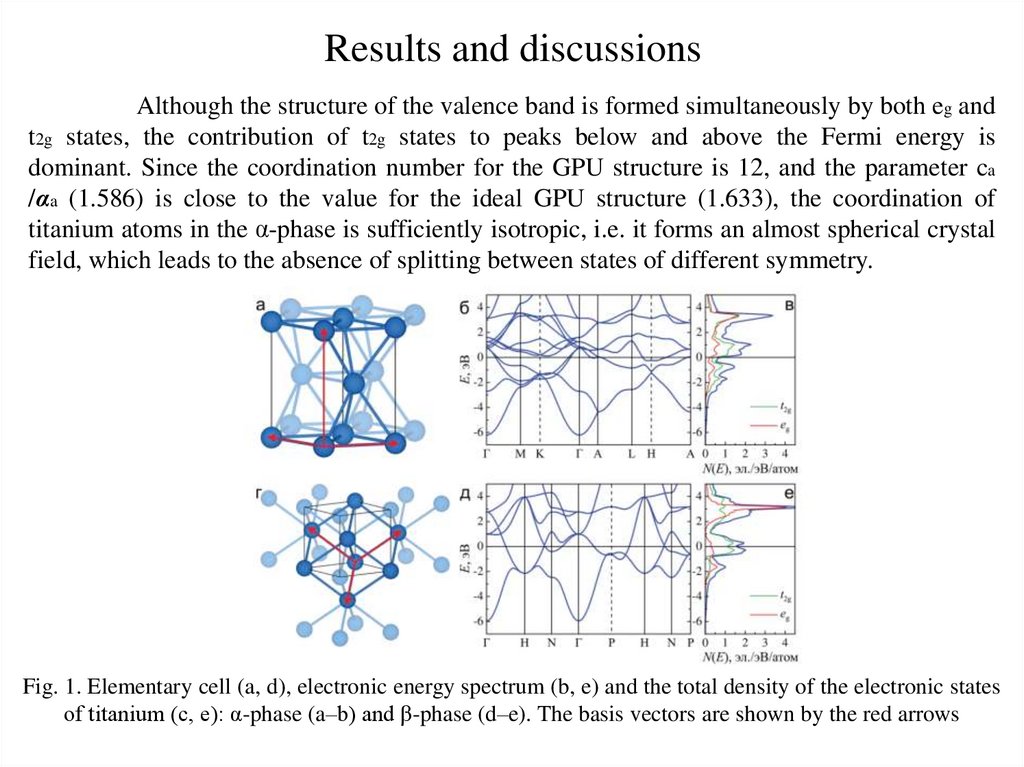
Results and discussionsAlthough the structure of the valence band is formed simultaneously by both eg and
t2g states, the contribution of t2g states to peaks below and above the Fermi energy is
dominant. Since the coordination number for the GPU structure is 12, and the parameter ca
/αa (1.586) is close to the value for the ideal GPU structure (1.633), the coordination of
titanium atoms in the α-phase is sufficiently isotropic, i.e. it forms an almost spherical crystal
field, which leads to the absence of splitting between states of different symmetry.
Fig. 1. Elementary cell (a, d), electronic energy spectrum (b, e) and the total density of the electronic states
of titanium (c, e): α-phase (a–b) and β-phase (d–e). The basis vectors are shown by the red arrows
6.
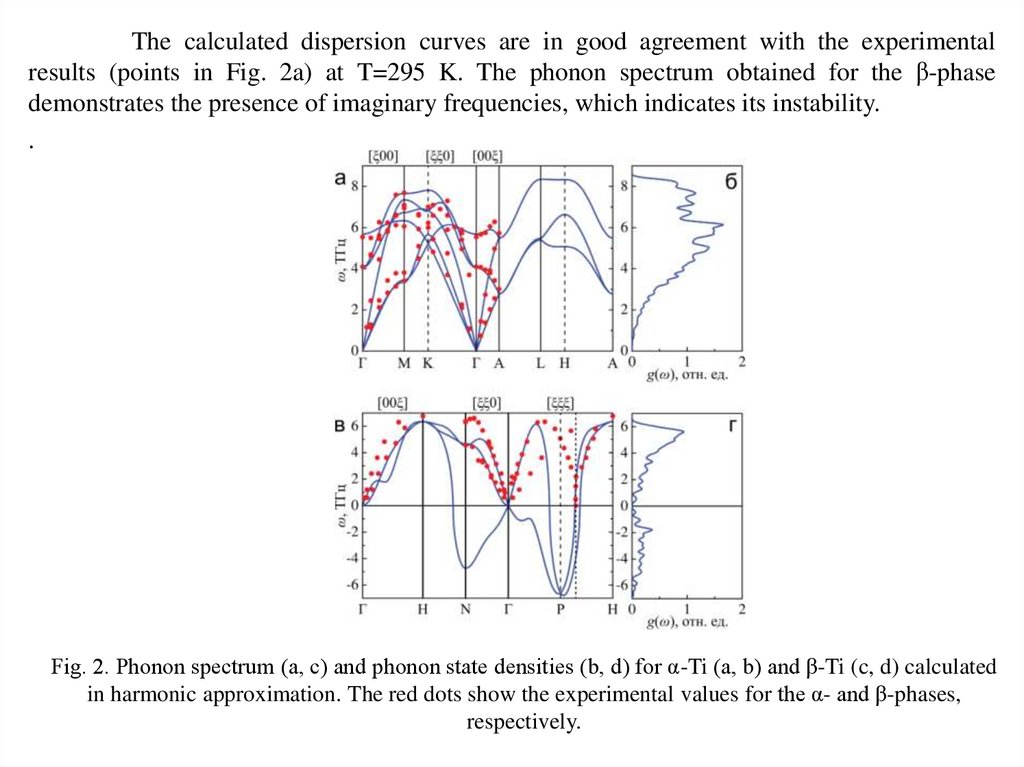
The calculated dispersion curves are in good agreement with the experimentalresults (points in Fig. 2a) at T=295 K. The phonon spectrum obtained for the β-phase
demonstrates the presence of imaginary frequencies, which indicates its instability.
.
Fig. 2. Phonon spectrum (a, c) and phonon state densities (b, d) for α-Ti (a, b) and β-Ti (c, d) calculated
in harmonic approximation. The red dots show the experimental values for the α- and β-phases,
respectively.
7.
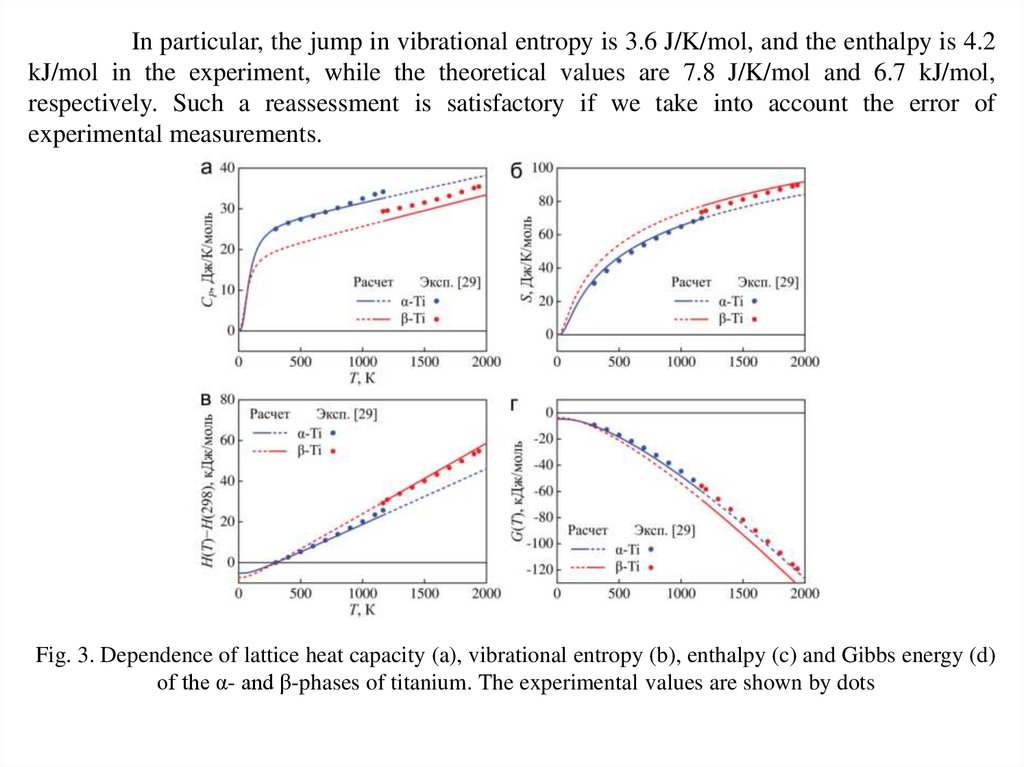
In particular, the jump in vibrational entropy is 3.6 J/K/mol, and the enthalpy is 4.2kJ/mol in the experiment, while the theoretical values are 7.8 J/K/mol and 6.7 kJ/mol,
respectively. Such a reassessment is satisfactory if we take into account the error of
experimental measurements.
Fig. 3. Dependence of lattice heat capacity (a), vibrational entropy (b), enthalpy (c) and Gibbs energy (d)
of the α- and β-phases of titanium. The experimental values are shown by dots
8.
ConclusionConclusion The atomic and electronic structure and thermodynamic properties of
the α- and β-phases of titanium are calculated by the method of projection coupled waves.
Analysis of the features of the electronic structure showed that β-Ti is unstable, since the
Fermi level falls into the peak of the density of states, although at a local minimum. It is
shown that the electronic states at the Fermi level are predominantly states of t2g symmetry.
The calculated phonon spectrum for α-Ti demonstrates only real frequencies, which confirms
the stability of this structure at low temperatures, while the theoretical spectrum agrees well
with the available experimental frequencies.
In the case of the β-phase, the theoretical phonon spectrum has imaginary
frequencies, which corresponds to the presence of soft modes in the experimental spectrum.
Negative frequencies are observed at point N on the border of the Brillouin zone (wave
vector 2π/a[1/2,1/2,0]) and in the vicinity of point P in the direction [ξ,ξ,ξ]. This suggests the
presence of several mechanisms of phase β→α transformation. The calculated
thermodynamic characteristics, such as lattice heat capacity, vibrational entropy and enthalpy,
also demonstrate satisfactory agreement with the experiment. This approach can be used to
analyze the forming phases of doped titanium.





 electronics
electronics








