Similar presentations:
Тема 1.3. Занятие 1. Методы обучения решения текстовых задач с помощью дробно-рациональных уравнений
1.
2.
1. Ваши слова соответствуют вашим мыслям, вы считаете, что можете позволить себе роскошь быть самим собой.Философское отношение к жизни позволяет вам одинаково достойно переживать и взлеты, и падения, вы фаталист и предпочитаете
достигать результата своим трудом.
2. Вы любите разнообразие и приключения. Вашей энергии тесно в повседневности, поэтому вы ищете шанс раскрасить будни.
Скука самый страшный ваш враг, вы стремитесь к познанию всего нового. Вы скупаете все технические новинки и разбираетесь в
них.
3. Ваше общество интересно для окружающих. Оптимизм и открытость притягивают к вам даже тех людей, без которых вы смогли
бы обойтись.
Ваши суждения вызывают доверие, а репутация на самом высоком уровне, хотя вы и не предпринимаете особых усилий к ее
сохранению.
4. Равновесие в мыслях и поступках позволяют вам сохранять спокойствие в самых сложных ситуациях. Ваши действия осмысленны
и поэтому вы редко проигрываете. Немногословный и очень надежный человек, с которым не страшны никакие испытания.
5. Вы радостно дышите полной грудью и берете от жизни по максимуму. Каждый день для вас наполнен счастьем, в любой
повседневной ситуации вы способны найти повод для оптимизма, поэтому вы не ищете приключений, ведь каждый день хорош сам
по себе.
6. Высокий уровень интеллекта, хорошая память и тяга к познанию, привлекает к вам людей, готовых учиться.
Ваш ум скор, вы способны быстро сделать выводы из небольшого количества исходных данных, поэтому люди готовы доверять вам
свои тайны и советоваться в сложных ситуациях.
3.
Курсы повышения квалификации «Развитие предметных компетенцийучителей математики 5-9 классов»
Тема 1.3 Методы обучения решения текстовых задач с
помощью дробно-рациональных уравнений, квадратных
уравнений
Занятие 1. Методы обучения решения текстовых задач с
помощью дробно-рациональных уравнений.
4.
РЕЗУЛЬТАТЫ ОБУЧЕНИЯРЕЗУЛЬТАТЫ ОБУЧЕНИЯ:
умеют определять вид задачи;
составляют математическую модель и объясняют алгоритм решения
текстовой задачи;
обосновывают выбор метода обучения.
5.
ПРИЕМ «ЗХУ»Заполните таблицу ЗХУ: столбец 1 – что вы знаете по теме занятия, столбец 2 – сформулируйте
вопросы, на которые вы хотите получить ответы.
Знаю
Хочу узнать
Узнал
6.
ЗАДАНИЕИНДИВИДУАЛЬНАЯ РАБОТА
Дайте характеристику каждого их них. Какие это уравнения?
7.
Стратегия «Вопрос-ответ»Дайте определение понятию
дробно-рациональные
уравнения ?
8.
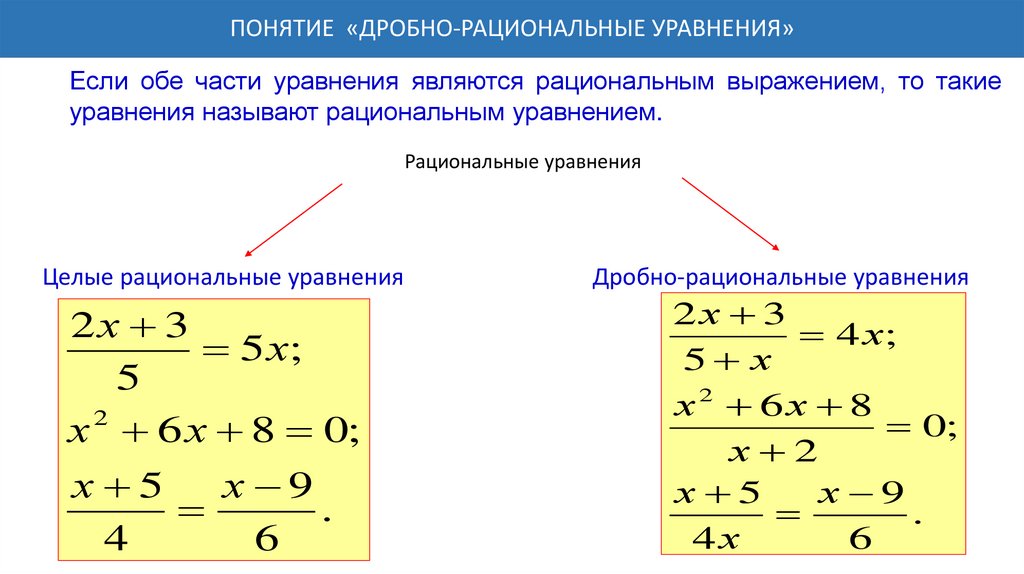
ПОНЯТИЕ «ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ»Если обе части уравнения являются рациональным выражением, то такие
уравнения называют рациональным уравнением.
Рациональные уравнения
Целые рациональные уравнения
2х 3
5 х;
5
2
х 6 х 8 0;
х 5
х 9
.
4
6
Дробно-рациональные уравнения
2х 3
4 х;
5 х
х2 6х 8
0;
х 2
х 5
х 9
.
4х
6
9.
ПОНЯТИЕ «ДРОБНО-РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ»Особенности решения задач на движения
S=vt, где s- расстояние,
v-скорость,
t-время
v=s/t
t=s/v
Если в условии не дан весь путь,
то его можно принять за 1.
Алгоритм решения задачи
1.
2.
3.
4.
5.
Внесем в таблицу известные величины ( расстояние
примем за 1)
Одну из неизвестных величин обозначим за х.
Остальные неизвестные величины выразим через х,
используя условие задачи или формулы.
Составим уравнение.
Решим уравнение и ответим на главный вопрос задачи.
Особенности решения задач на работу
А=Рt, где А-работа
Р- производительность труда
t- время
Р=А/t
t=А/Р
Если в условии не дана вся работа, то её можно принять за 1
Общая производительность равна сумме производительностей.
10.
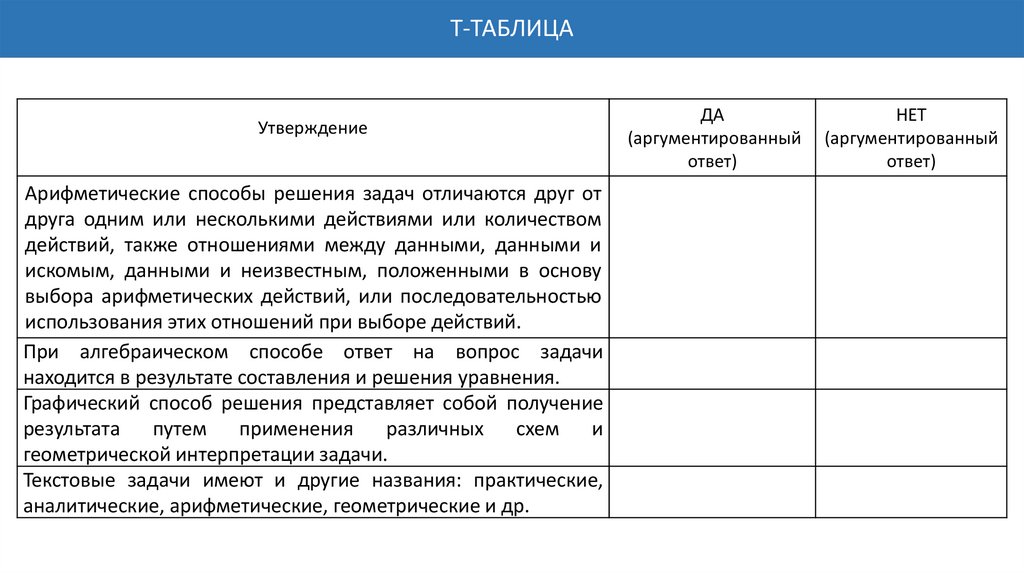
Т-ТАБЛИЦАУтверждение
Арифметические способы решения задач отличаются друг от
друга одним или несколькими действиями или количеством
действий, также отношениями между данными, данными и
искомым, данными и неизвестным, положенными в основу
выбора арифметических действий, или последовательностью
использования этих отношений при выборе действий.
При алгебраическом способе ответ на вопрос задачи
находится в результате составления и решения уравнения.
Графический способ решения представляет собой получение
результата
путем
применения
различных
схем
и
геометрической интерпретации задачи.
Текстовые задачи имеют и другие названия: практические,
аналитические, арифметические, геометрические и др.
ДА
(аргументированный
ответ)
НЕТ
(аргументированный
ответ)
11.
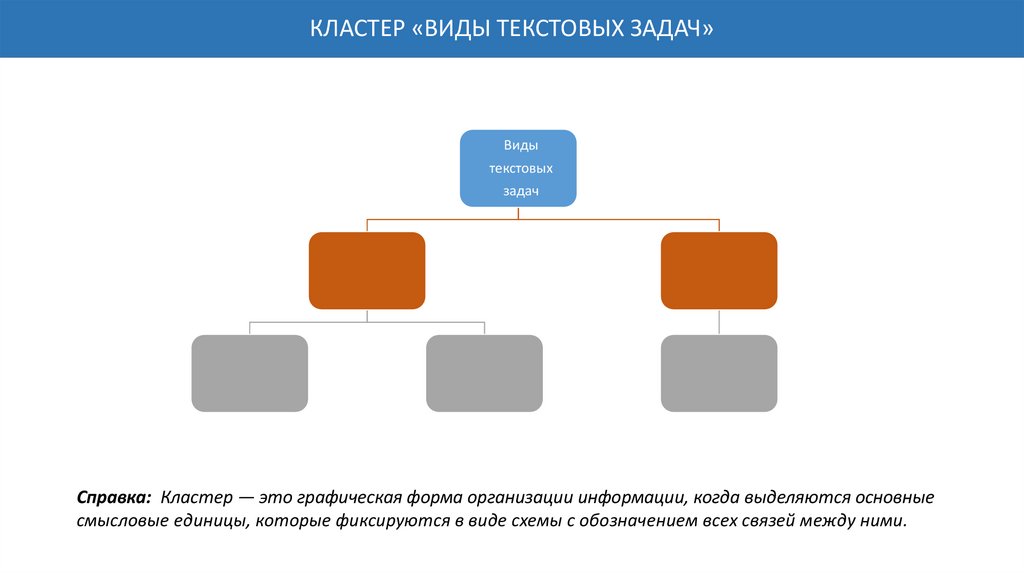
КЛАСТЕР «ВИДЫ ТЕКСТОВЫХ ЗАДАЧ»Виды
текстовых
задач
Справка: Кластер — это графическая форма организации информации, когда выделяются основные
смысловые единицы, которые фиксируются в виде схемы с обозначением всех связей между ними.
12.
ВИДЫ ЗАДАЧЗадачи на движение по воде.
Задачи на движение по местности.
Задачи на работу.
Задачи на нахождение дробей и т.д.
13.
s – расстояние, v – скорость, t - времяs = vt
t=s:v
v=s:t
s=v:t
t=s∙v
t:v=s
v=t:s
v∙t=s
14.
Велосипедист от озерадо деревни
ехал со ехал
скоростью
15 км/ч, а обратно
– соа
Велосипедист
от озера
до деревни
со скоростью
15 км/ч,
скоростью
Сколько времени
ушлоСколько
у него на дорогу
от озера
до деревни,
обратно10– км/ч.
со скоростью
10 км/ч.
времени
ушло
у него
если на весь путь туда и обратно велосипедист затратил 1 ч? Велосипедист от
на
дорогу
от
озера
до
деревни,
если
на
весь
путь
туда
и
озера до деревни ехал со скоростью 15 км/ч, а обратно – со скоростью 10 км/ч.
обратно
велосипедист
Сколько
времени
ушло у негозатратил
на дорогу 1
отч?
озера до деревни, если на весь путь
туда и обратно велосипедист затратил 1 ч?
Пусть
ч – время, затраченное
на дорогу
от озера до деревни. Какое
s –х расстояние,
v – скорость,
t - время
из уравнений соответствует условию задачи?
s = vt
Скорость
Время
Расстояние
От озера
15 км/ч
хч
15х км
От деревни
10 км/ч
(1 – х) ч
1ч
10(1 – х) км
15.
СкоростьВремя
Расстояние
От озера
15 км/ч
хч
15х км
От деревни
10 км/ч
(1 – х) ч
10(1 – х) км
Расстояние
15х км
одно и=то же, т.е одинаковое.
10(1 – х) км
А. 15х = 10(1 – х)
Б.
15
10
+
х
1–х
В. 15х + 10(1 – х) = 1
Г. 15(1 – х ) = 10х
верно
1
неверно
v:t
s2 = t
s 1 неверно
v 1 неверно
t 2 = v 2 t1
16.
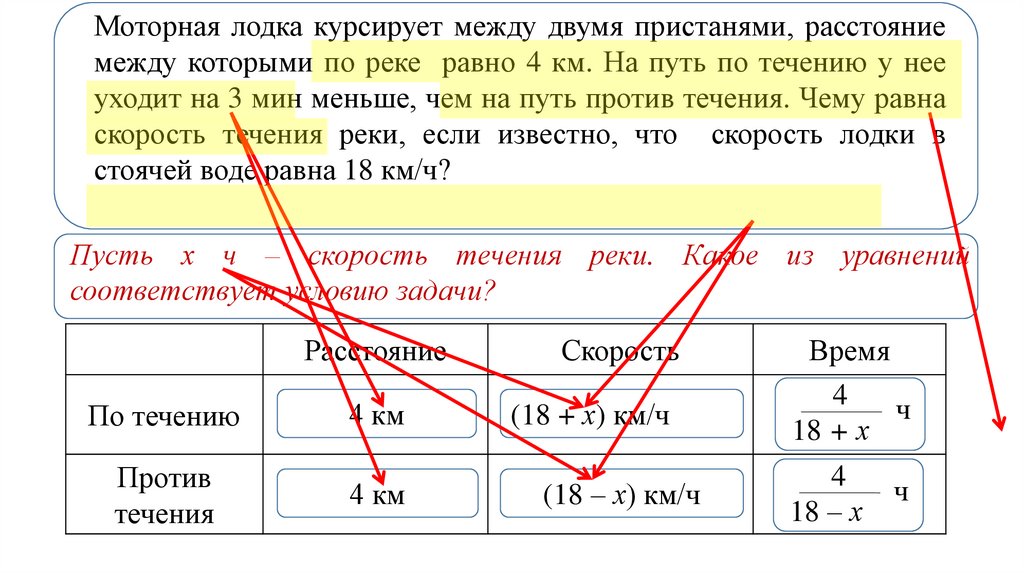
Моторнаялодка
курсирует
между
пристанями,
расстояние
Велосипедист
от озера
до деревни
ехал содвумя
скоростью
15 км/ч, а обратно
– со
между которыми
по реке
На от
путь
подотечению
у нее
скоростью
10 км/ч. времени
ушлоравно
у него 4накм.
дорогу
озера
деревни, если
на
уходит
меньше,
чем на затратил
путь против
течения. Чему
равна
весь
путь на
туда3 имин
обратно
велосипедист
1 ч? Велосипедист
от озера
до
деревни
ехалтечения
со скоростью
15 км/ч,
обратно – сочто
скоростью
10 км/ч.лодки
Сколько
скорость
реки,
еслиа известно,
скорость
в
времени ушло
него на18дорогу
стоячей
водеуравна
км/ч?от озера до деревни, если на весь путь туда и
обратно велосипедист затратил 1 ч? н
Пусть х ч – скорость течения реки. Какое из уравнений
t=s:v
соответствует условию задачи?
Расстояние
По течению
Против
течения
4 км
4 км
Скорость
(18 + х) км/ч
(18 – х) км/ч
Время
4
ч
18 + х
4
18 – х
ч
17.
РасстояниеПо течению
Против
течения
4 км
4 км
Скорость
(18 + х) км/ч
(18 – х) км/ч
Время
4
ч
18 + х
4
18 – х
3 меньше,
Время по течению на 3 мин
чем время против
1
3 мин =
ч=
ч
60
течения.
20
4
1
2
–
верно
А. 18 – х
18 + х
20
18 – х – 18 + х
3
неверно
Б.
v :s
4
4
1
4
2
t
t
неверно
В. 18 + х – 18 – х
1
2
20
Г. 4(18 + х) – 4(18 – х) = 3
s ∙v
неверно
ч
18.
Велосипедист от озера до деревни ехал со скоростью 15 км/ч, а обратно – соОт города
до Сколько
поселкавремени
автомобиль
доехал
за 3 отч.озера
Если
бы он
скоростью
10 км/ч.
ушло у него
на дорогу
до деревни,
увеличил
25 км/ч,
то затратил
бы на
этот
путь на 1отч
если
на весьскорость
путь туда ина
обратно
велосипедист
затратил
1 ч?
Велосипедист
меньше.
Чему ехал
равно
расстояние
города
до поселка?
озера
до деревни
со скоростью
15 от
км/ч,
а обратно
– со скоростью 10 км/ч.
Сколько времени ушло у него на дорогу от озера до деревни, если на весь путь
туда и обратно велосипедист затратил 1 ч?
Пусть х км – расстояние от города до поселка. Какое уравнение
v=s:t
соответствует условию задачи?
Расстояние (км)
Проехал
Мог проехать
х
х
Время
(ч)
Скорость
(км/ч)
3
х
3
2
на 1 ч меньше
х
2
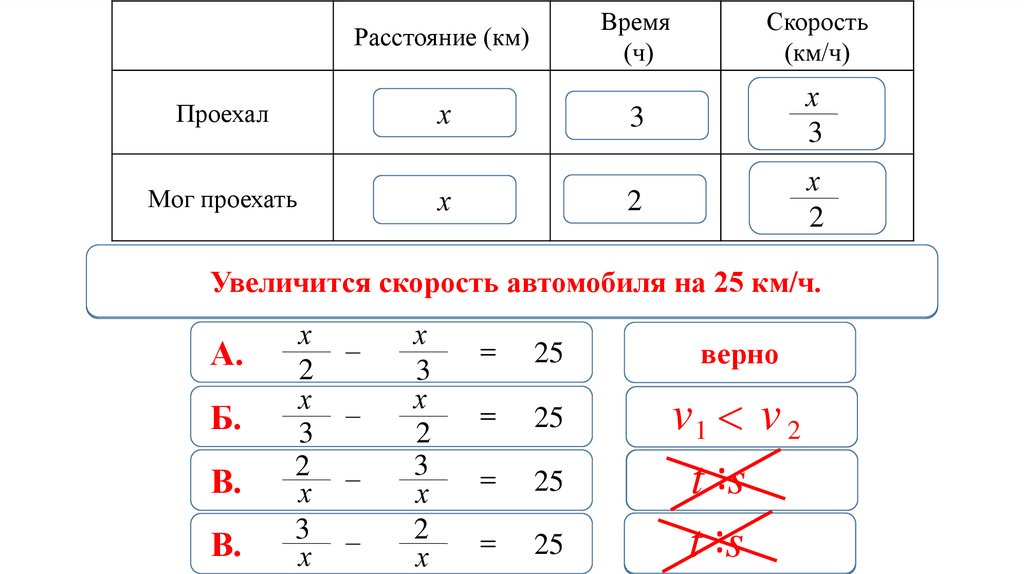
19.
Расстояние (км)Проехал
Мог проехать
х
х
Время
(ч)
Скорость
(км/ч)
3
х
3
2
х
2
Времени на путь затрачено больше, значит скорость
Увеличится скорость автомобиля на 25 км/ч.
движения меньше.
х
х
25
–
верно
А.
2
3
х
х
25
–
Б.
vневерно
1 v2
2
3
3
2 –
25
:
неверно
В.
t
s
х
х
2
3 –
25
неверно
В.
t :s
х
х
20.
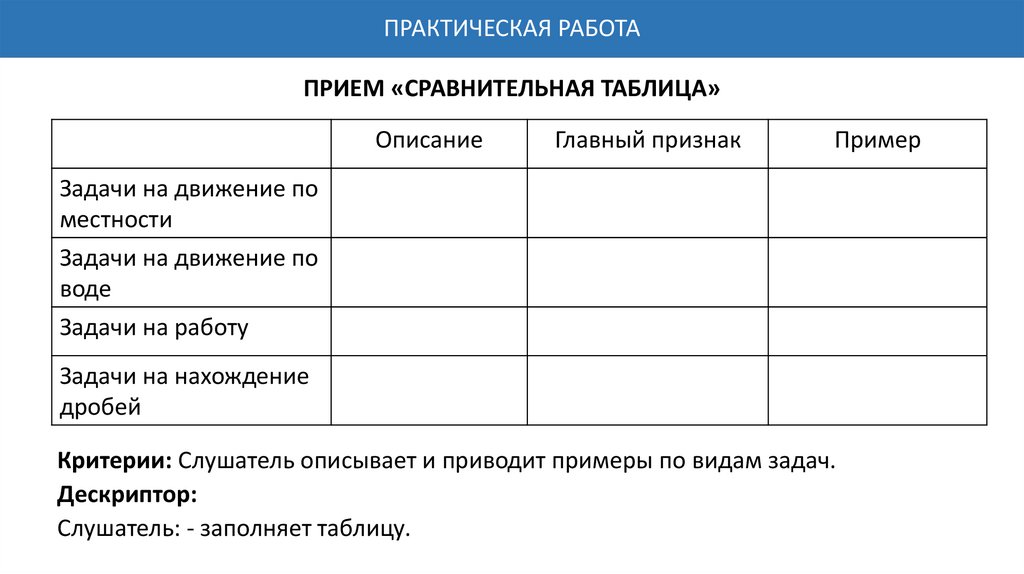
ПРАКТИЧЕСКАЯ РАБОТАПРИЕМ «СРАВНИТЕЛЬНАЯ ТАБЛИЦА»
Описание
Главный признак
Пример
Задачи на движение по
местности
Задачи на движение по
воде
Задачи на работу
Задачи на нахождение
дробей
Критерии: Слушатель описывает и приводит примеры по видам задач.
Дескриптор:
Слушатель: - заполняет таблицу.
21.
ВЗАИМООЦЕНИВАНИЕПрием «Сэндвич похвалы»
«Хорошая новость»
У вас получилось …
«Плохая новость»
Считаем, что нужно изменить…, потому что …
«Хорошая новость»
Вы сможете улучшить результат, если …
22.
ЗАДАНИЕПрием «Зигзаг»
Разбейтесь на
группы по 5 человек
и решают текстовые
задачи (задачи на
движение по
местности, на
движение по воде,
на работу, на
нахождение дробей,
финансовых задач)
1 этап
Объединяются в 5
«экспертных» групп
по видам текстовых
задач, обсуждают
ход решения задач,
составляют постер
«Рекомендации по
методам решения
текстовых задач».
Презентуют постеры
другим группам
Возвращаются в
«домашние» группы
и составляют
текстовые задачи,
решаемых с
помощью дробнорациональных
уравнений
2 этап
3 этап
4 этап
23.
ПРИЕМ «ЗХУ»Заполните таблицу ЗХУ: заполняют третий столбец таблицы: что вы узнали на занятии нового.
Знаю
Хочу узнать
Узнал
24.
ВЗАИМООЦЕНИВАНИЕПрием «Рюкзак»
• Передавая рюкзак, зафиксируйте свой успех и
назовите лучшие рекомендации.
25.
РЕФЛЕКСИЯПрием «Пять вопросов»
Как бы вы
назвали
сегодняшне
е название?
Что было
самым
важным на
занятии?
Что для вас
было легко
(трудно)?
Довольны
ли вы своей
работой?
За что вы
хотите
похвалить
себя или
кого-то из
коллег?
26.
Занятие 2. Методы обучения решения текстовых задачс помощью квадратных уравнений.
27.
РЕЗУЛЬТАТЫ ОБУЧЕНИЯРЕЗУЛЬТАТЫ ОБУЧЕНИЯ:
умеют определять вид задачи;
составляют математическую модель и объясняют алгоритм решения
текстовой задачи;
обосновывают выбор метода обучения.
28.
«КОРЗИНА ИДЕЙ» (фактов, понятий).???
???
???
???
???
Корзина идей:
Каждый слушатель записывает в
тетради все, что может быть
отнесено к решению задач
29.
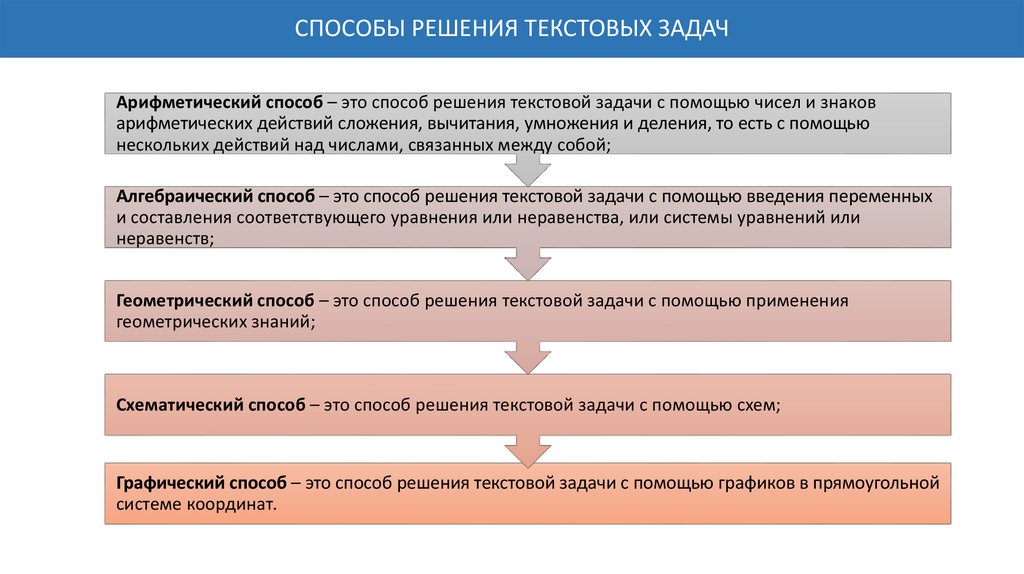
СПОСОБЫ РЕШЕНИЯ ТЕКСТОВЫХ ЗАДАЧАрифметический способ – это способ решения текстовой задачи с помощью чисел и знаков
арифметических действий сложения, вычитания, умножения и деления, то есть с помощью
нескольких действий над числами, связанных между собой;
Алгебраический способ – это способ решения текстовой задачи с помощью введения переменных
и составления соответствующего уравнения или неравенства, или системы уравнений или
неравенств;
Геометрический способ – это способ решения текстовой задачи с помощью применения
геометрических знаний;
Схематический способ – это способ решения текстовой задачи с помощью схем;
Графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной
системе координат.
30.
ЭТАПЫ РЕШЕНИЯ ТЕКСТОВОЙ ЗАДАЧИ1. Анализ условия задачи
2. Объяснение к составлению уравнения
3. Составление уравнения
4. Решение уравнения и запись ответа
5. Анализ решения задачи
31.
ГРУППОВАЯ РАБОТАПрием «Посол»
• Первый этап – разбейтесь на группы по этапам и разработайте
способы устранения затруднений.
• Второй этап – выберите «посла» и презентуйте работу другим
группам
32.
ВЗАИМООЦЕНИВАНИЕ• Дайте обратную связь друг другу.
• Используйте прием «Две звезды,
одно пожелание»: звезда –
лучшее, пожелание – что нужно
доработать.
Вам
удалось
..
Вам
необходимо
доработать …
/поработать
над…
У вас
получи
лось..
33.
ИГРА «НАУЧИ МЕНЯ»• Слушатели делятся на команды «экспериментаторов» и «экспертов».
• Экспериментаторам: определить эффективный способ решения текстовых
задач и интерактивных методов обучения и показать, как он применяется
на практике для достижения данной цели урока.
• Экспертам: внимательно просмотреть, прослушать выступление
«экспериментаторов» и дать обратную связь.
• Задание для «экспериментаторов» и «экспертов» – поменяться ролями.
34.
ЗАДАНИЕГРУППОВАЯ РАБОТА «КАРУСЕЛЬ»
Задача №1
Задача №2
Задача №3
35.
МИНИ-ПРОЕКТ «ЗАДАЧА ДНЯ»• Мини-проект «Задача дня»:
• Путем вытягивания карточек с рисунками «Велосипедиста»,
«Автомобилиста», «Фермеры», «Туристы», составляют задачи на
производительность труда и на производительность различных
механизмов (труб, насосов и т. д.).
36.
ВЗАИМООЦЕНИВАНИЕ• Дайте обратную связь друг другу.
• Используйте прием «Книга
отзывов и предложений»:
Слушатели пишут отзыв о
представленных задачах и
методах решения, дают свои
предложения.
37.
РЕФЛЕКСИЯ «ОБЛАКО СЛОВ»Слушатели рефлексируют
содержание занятия,
собственной деятельности
и планирования своей
работы в «Облако слов» на
платформе Wooclap
38.
Занятие 3. Проектирование фрагмента урока дляобучения решению текстовых задач.
39.
РЕЗУЛЬТАТЫ ОБУЧЕНИЯРЕЗУЛЬТАТЫ ОБУЧЕНИЯ:
Умеет проектировать фрагмент урока и систематизировать
методы и подходы решения текстовых задач
40.
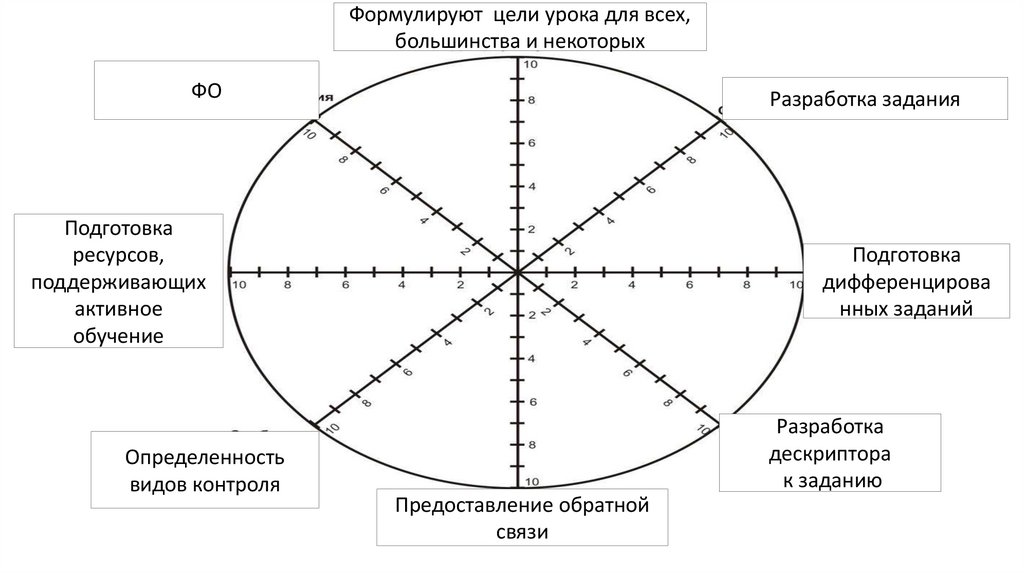
Формулируют цели урока для всех,большинства и некоторых
ФО
Разработка задания
Подготовка
ресурсов,
поддерживающих
активное
обучение
Определенность
видов контроля
Подготовка
дифференцирова
нных заданий
Разработка
дескриптора
к заданию
Предоставление обратной
связи
41.
БЛАГОДАРИМЗА ВНИМАНИЕ!



























 mathematics
mathematics








