Similar presentations:
Решение текстовых задач с помощью дробно - рациональных уравнений
1.
2.
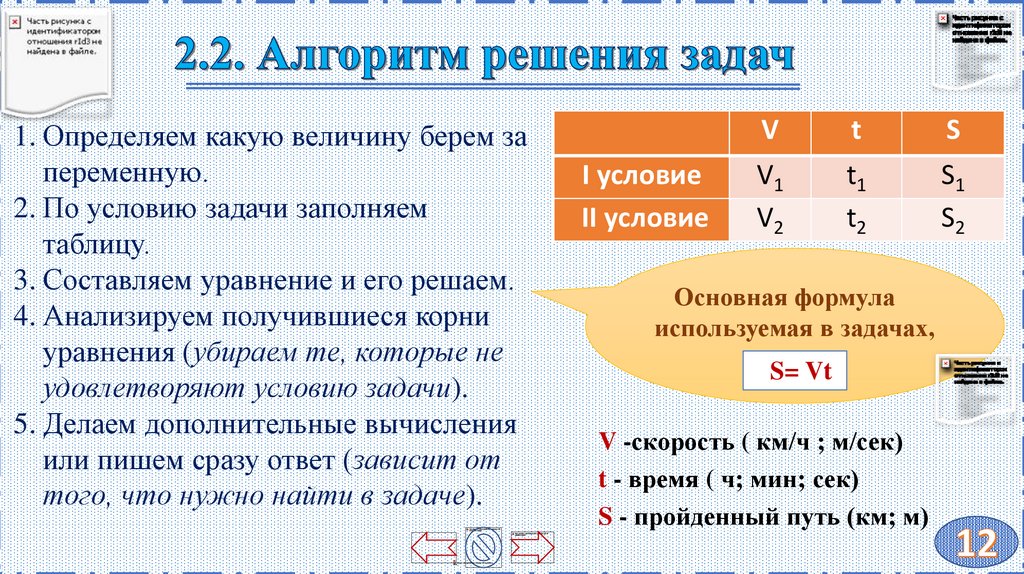
Задание № 2:Алгоритм решения дробного
рационального уравнения.
1. Все переносим в левую часть.
2. Приводим дроби к общему
знаменателю.
3. Заменяем уравнение на
систему:
числитель = 0,
ቊ
знаменатель ≠ 0.
Дробь равна нулю,
тогда и только
тогда, когда
числитель равен
нулю, а знаменатель
нулю не равен.
3.
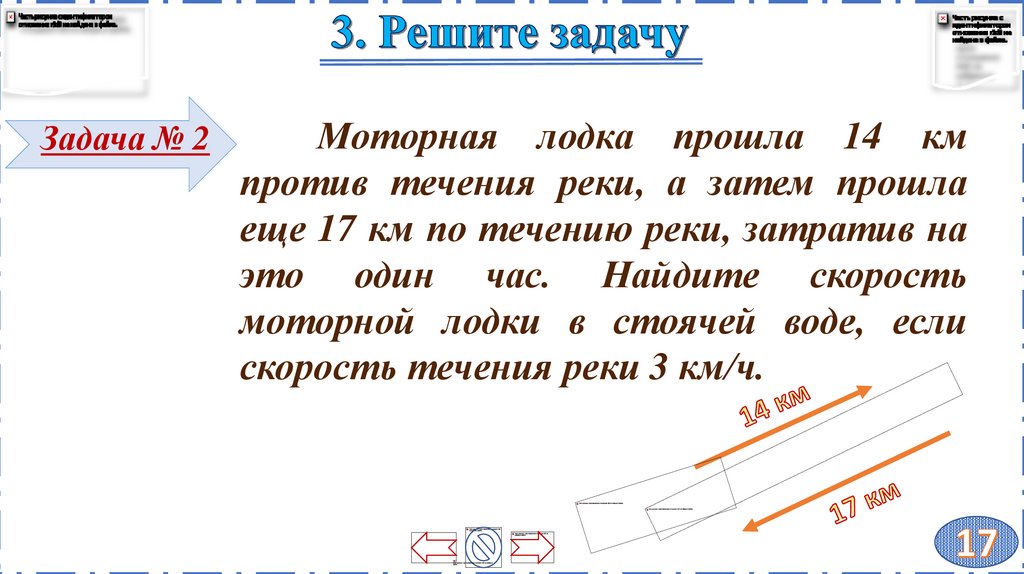
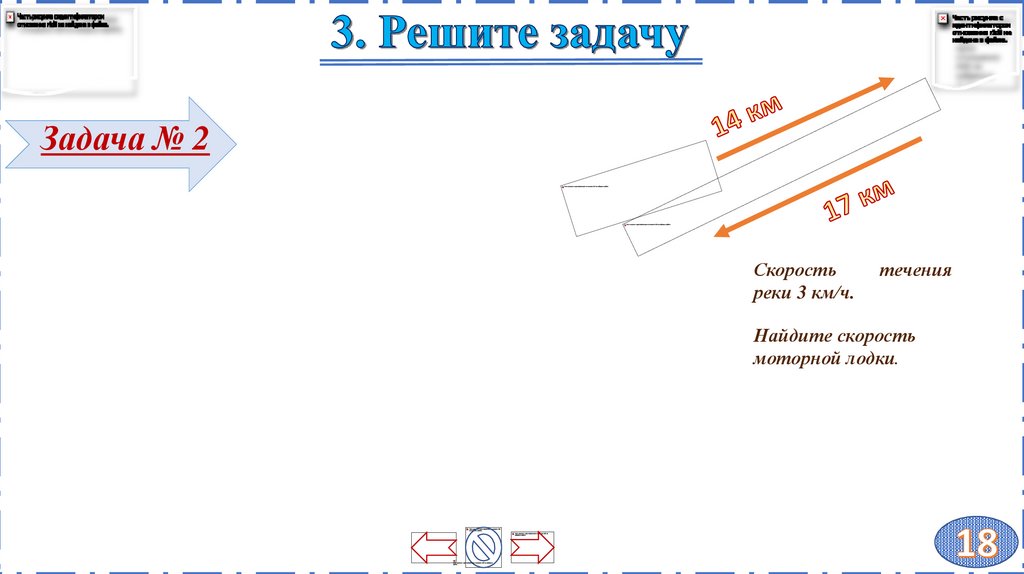
Задача № 1Из пунктов А и В, расстояние между
которыми
27 км, вышли одновременно
навстречу друг другу два
пешехода и
встретились в 15 км от А. Найдите
скорость пешехода, шедшего из А, если
известно, что он шёл со скоростью, на 2
км/ч большей, чем второй
пешеход, и
сделал в пути получасовую остановку.
4.
Задача № 1А
15км
В
27 км
5.
Решение задачи №1
Пусть скорость пешехода, шедшего из А равна х км/ч,
тогда скорость пешехода шедшего из В равна (х-2) км/ч.
Пешеход из А
Пешеход из Б
V
t
S
х
х-2
t1
t2
15
12
Пешеход из А прошел 15 км, а расстояние между пунктами 27 км, следовательно
пешеход их В прошел 12 км. 27-15=12.
По условию пешеход из А сделал в пути получасовую остановку, значит он шел
меньше времени на 0,5 ч . Это условие можно записать так t1< t2 на 0,5 ч. или t2 - t1 = 0,5.
Получаем уравнение:
12
х−2
15
- = 0,5
х
6.
Решение задачи №1
12
х−2
15
- = 0,5,
х
12х−15 х−2 −0,5х х−2
=0,
х(х−2)
12х − 15 х − 2 − 0,5х х − 2 = 0,
ቊ
х х − 2 ≠ 0;
−0,5












 mathematics
mathematics








