Similar presentations:
Решение текстовых задач с помощью дробных рациональных уравнений
1.
Решение задач с помощьюдробных рациональных
уравнений
МАОУ СШ с.Мошенское, Новгородской
области
Учитель математики: Растатурова Л.В.
2.
Задачи на движениеВ задачах на движение
рассматриваются три
взаимосвязанные величины:
S - расстояние (пройденный
путь),
t - время движения
V - скорость
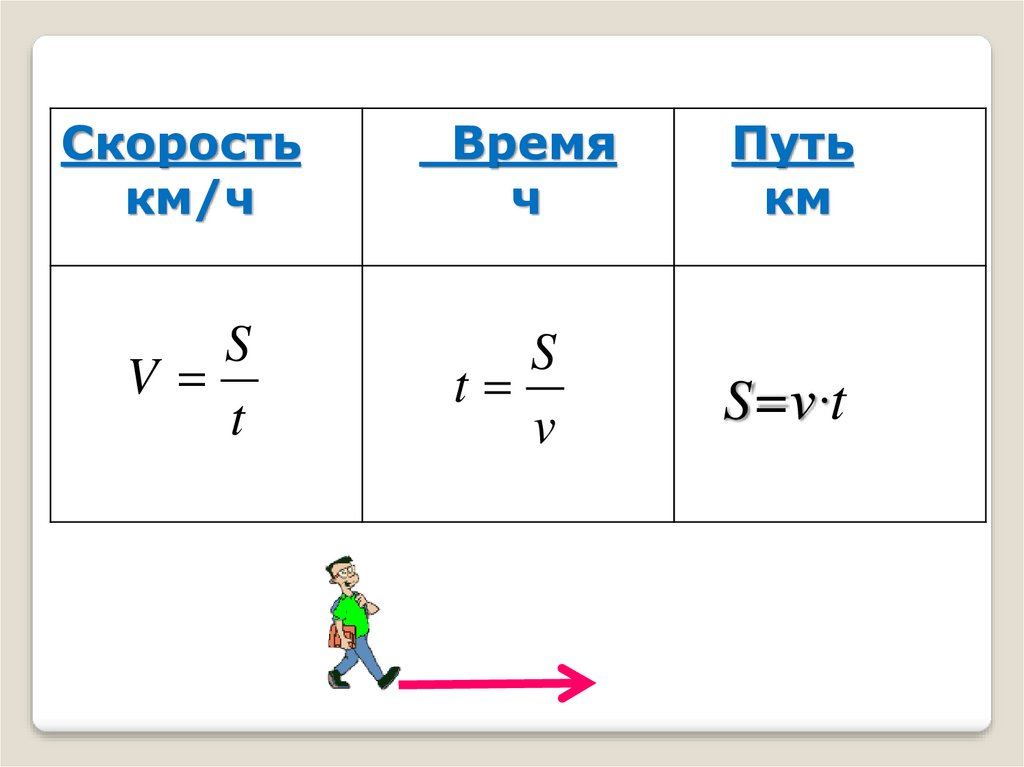
3.
Скоростькм/ч
S
V
t
Время
ч
Путь
км
S
t
v
S=v·t
4.
Задача.Из города А в город В, расстояние между
которыми 120 км, выехали
одновременно два велосипедиста.
Скорость первого на 3 км/ч больше
скорости второго, поэтому он прибыл в
город В на 2 ч раньше. Определите
скорость велосипедистов
5.
Решение.Пусть х км/ч – скорость второго велосипедиста
, км/ч
1
велосипедист
2
велосипедист
х 3
км/ч
х
км/ч
s, км
t, ч
120
x 3 ч
120
x
ч
120
км
120
км
Зная, что первый велосипедист прибыл в город В
раньше на 2 ч, чем второй, составим уравнение:
6.
Решение120
120
2
х
х 3
60
60
1
x x 3
х 3х 180 0, (1)
х( х 3) 0
x
2
(1) х 3х 180 0
2
3 27
3 27
15; х 2
12
1
2
2
Число -15 противоречит смыслу задачи
Если х=12, то х(х+3)≠0, верно
12 км/ч – скорость второго велосипедиста
15 км/ч – скорость первого велосипедиста
Ответ: 12 км/ч; 15 км/ч.
7.
Задачи на движениепо течению и против течения
реки
Собственная скорость катера Vc
Скорость течения реки Vт
скорость катера по течению Vc+Vт
скорость катера против течения Vc-Vт
8.
Задача.Катер отправился в путь в 15 часов,
прошел 7км против течения реки и сделал
остановку на 2 часа. После этого он
прошел еще 27 км по течению реки и
прибыл в пункт назначения в 19 часов.
Найти собственную скорость катера , если
скорость течения реки 2 км/ч.
9.
Решение.Движение
По течению
Против
течения
v, км / ч
х 2
х 2
vсобст
х
vтечения
2
s, км
t, ч
Км/ч
27
х 2
ч
27
Км/ч
7
х 2
ч
7
км/ч
км/ч
км
км
10.
Катер отправился в путь в 15 часов, прошел7км против течения реки и сделал остановку на 2 часа.
После этого он прошел еще 27 км по течению реки и
прибыл в пункт назначения в 19 часов. Найти
собственную скорость катера , если скорость
течения реки 2 км/час.
Вычислим время движения катера
Составим уравнение
Ответ: 16 км/ч
7
27
2
х 2 х 2
11.
Задачи на работу, совместную работуПроизводительностью
называют работу,
выполненную за единицу
времени.
Производительность = работа/время
12.
Задача.Заказ на 180 деталей первый рабочий
выполняет на 3 часа быстрее, чем
второй. Сколько деталей в час делает
второй рабочий, если известно, что
первый за час делает на 3 детали
больше?
13.
Решение.Работа
Производитель
ность
Первый
рабочий
х 3
Второй
рабочий
х
детали
деталей
Время
180
х 3
180
х
час
час
Объём
работы
180
деталей
180
деталей
14.
Зная, что первый рабочий выполняет заказна 3 часа быстрее, чем второй,
составим уравнение:
180
180
3
х
х 3
Ответ :12деталей.
15.
ЗадачаПри совместной работе двух кранов разгрузку баржи
закончили за 6 ч. Сколько времени потребовалось бы
каждому крану отдельно, если известно, что первому
для этого требуется на 5 ч больше, чем второму?
Работа
Первый
кран
Второй
кран
Вместе
Производительность (скорость)
1
х 5
1
х
1
6
Время
х 5
х
6ч
Объём работы
ч
1
ч
1
1
16.
Решение.Зная, что при совместной работе двух кранов
разгрузку баржи закончили за 6 ч,
составим уравнение:
1
1
1
х
х 5
6
Ответ : 15ч;10ч.
17.
Задачи на смеси, растворы,сплавы
Метод квадрата (метод Пирсона)
Делаем таблицу (рисунок): в первой строке
концентрация первого раствора, а под ней – второго.
Посередине, между известными концентрациями
растворов, расположим неизвестную нам
концентрацию смеси, обозначив ее за х . Теперь
проводим стрелки, как показано на рисунке, и на
конце стрелочек записываем разности. При записи
разностей правило простое: надо вычитать из
большего меньшее. В начале каждой строчки впишем
массу растворов 1 и 2.
18.
масса1раствор
концентрация
%
%
%
2раствор
%
%
Метод квадрата (метод Пирсона)
19.
Задача.В сосуд, содержащий 5 кг
12-процентного
водного раствора некоторого
вещества, добавили 7 кг воды.
Сколько процентов составляет
концентрация получившегося
раствора?
20.
масса1раствор
5кг
концентрация
12 %
х%
х
2раствор
%
7кг
0%
12 - х %
21.
Решение.Решаем полученную пропорцию:
Ответ: концентрация смеси
равна 5%.
22.
Задача.Первый сплав содержит 10%
меди, второй — 40% меди.
Масса второго сплава больше
массы первого на 3 кг. Из этих
двух сплавов получили третий
сплав, содержащий 30% меди.
Найдите массу третьего сплава.
23.
масса1раствор
Х кг
концентрация
10 %
10%
30
2раствор
%
Х+3 кг
40 %
20 %
Составляем пропорцию.
10:20=х: (х+3)
Решаем.
2х=х+3
х=3.
х+3=6.
Масса третьего сплава, очевидно, сумма первых
двух: 9кг.
Ответ: 9 кг.
24.
Задачидля самостоятельного решения.
1. Расстояние в 400 км скорый поезд прошел на
час быстрее товарного. Какова скорость каждого
поезда, если скорость товарного поезда на 20км/ч
меньше скорого?
2. Катер прошел 8км по течению реки и 16 км
против течения , затратив на весь путь 45
минут. Какова скорость движения катера по
течению, если собственная скорость катера
равна 20 км/ч 3?
25.
3. Первая труба пропускает на 1 литр воды в минутуменьше, чем вторая. Сколько литров воды в
минуту пропускает первая труба, если резервуар
объемом 110 литров она заполняет на 2 минуты
дольше, чем вторая труба заполняет резервуар
объемом 99 литров?
4. Через две трубы бассейн наполняется водой за 5
часов. Сколько потребовалось бы для наполнения
бассейна только через первую трубу, если через
неё бассейн наполняется на 24 часа быстрее, чем
через вторую?
5. Смешали некоторое количество 15-процентного
раствора некоторого вещества с таким же
количеством 19-процентного раствора этого
вещества. Сколько процентов составляет
концентрация получившегося раствора?
























 mathematics
mathematics








