Similar presentations:
Оптимизационные экономико-математические модели
1.
Оптимизационные экономикоматематические моделиУтакаева Ирина Хайрлыевна
доцент
2.
Проверка связиЕсли у вас нет звука:
● убедитесь, что на вашем устройстве
и на колонках включен звук
● обновите страницу вебинара (или
закройте страницу и заново
присоединитесь к вебинару)
● откройте вебинар в другом браузере
● перезагрузите компьютер (ноутбук)
и заново попытайтесь зайти
Поставьте в чат:
+ если меня видно и слышно
– если нет
3.
Правила участия1
2
Приготовьте блокнот и ручку, чтобы записывать важные мысли и
идеи
Продолжительность вебинара – 6 часов
3
Вы можете писать свои вопросы в чате
4
Необходим компьютер с подключением к интернет
4.
О спикере:● Кандидат физико-математических наук
● Доцент департамента математики
Утакаева Ирина Хайрлыевна
t.me/ihutakaeva
5.
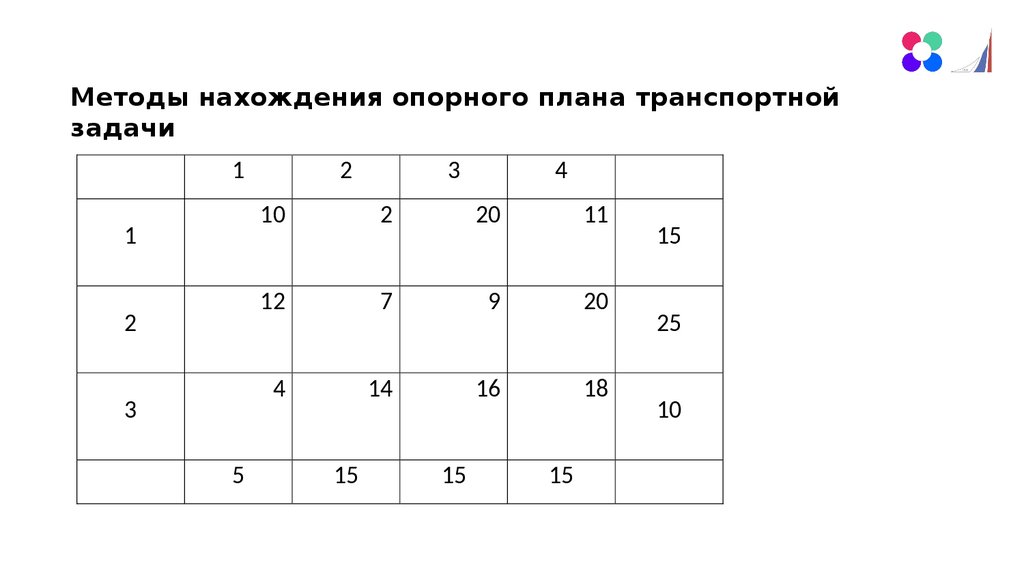
Практика6.
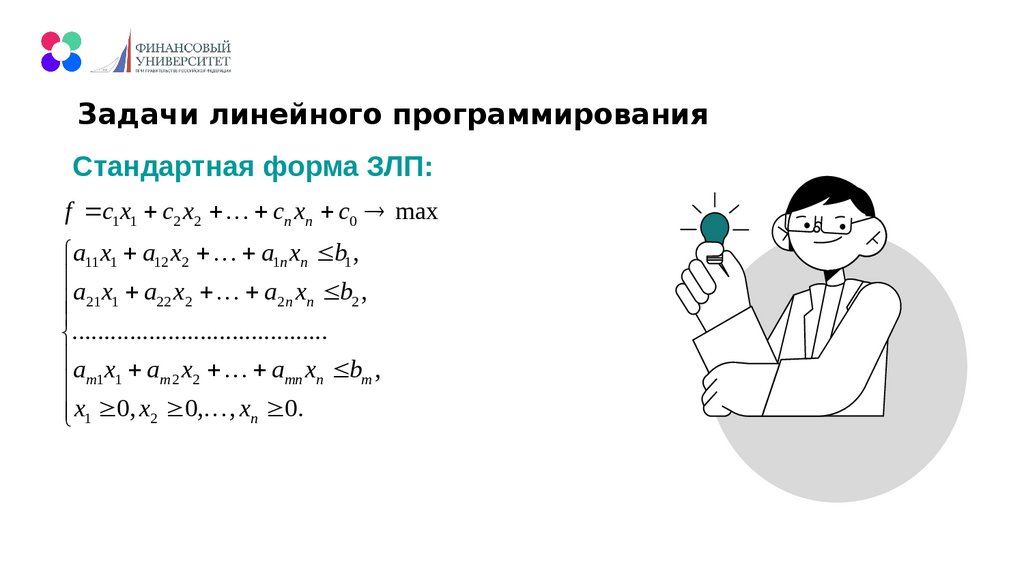
Задачи линейного программированияСтандартная форма ЗЛП:
f c1 x1 c2 x2 cn xn c0 max
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
2n n
2
21 1 22 2
........................................
a x a x a x b ,
mn n
m
m1 1 m 2 2
x1 0, x2 0, , xn 0.
7.
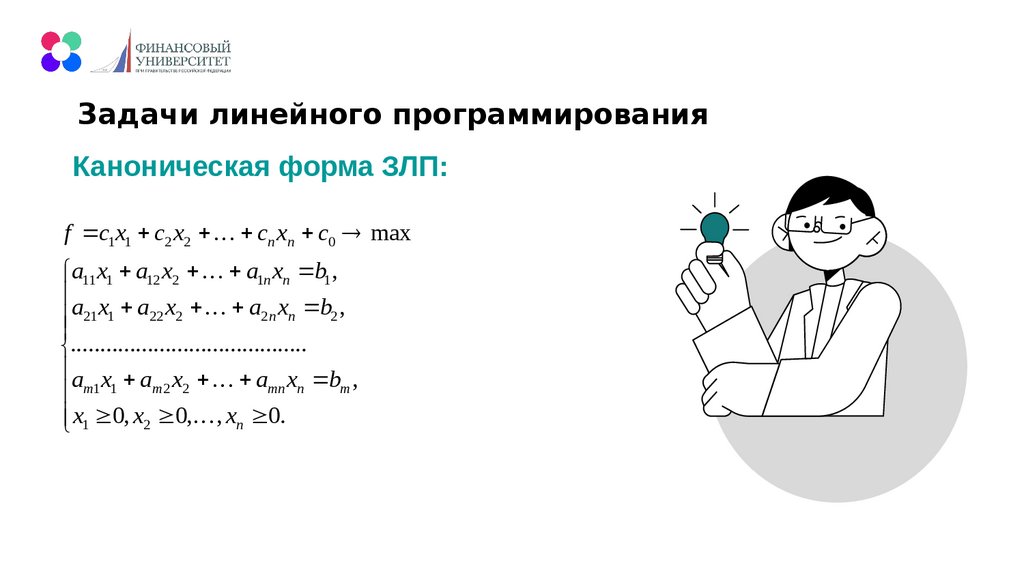
Задачи линейного программированияКаноническая форма ЗЛП:
f c1 x1 c2 x2 cn xn c0 max
a11 x1 a12 x2 a1n xn b1 ,
a x a x a x b ,
2n n
2
21 1 22 2
........................................
a x a x a x b ,
mn n
m
m1 1 m 2 2
x1 0, x2 0, , xn 0.
8.
Задачаоптимального
использования
ресурсов
Пример 1. В распоряжении фабрики имеется
определённое количество ресурсов: рабочая
сила,
деньги,
сырье,
оборудование,
производственные площади и т.п. Например,
пусть это будут ресурсы трёх видов: рабочая
сила (80 чел.-дней), сырье (480 кг) и
оборудование (130 станко-часов). Фабрика
может выпускать ковры четырёх типов.
Информация о количестве единиц каждого
ресурса,
необходимых
для
производства
одного ковра каждого типа, и доходах,
получаемых
предприятием
от
единицы
каждого типа товаров, приведена в таблице.
9.
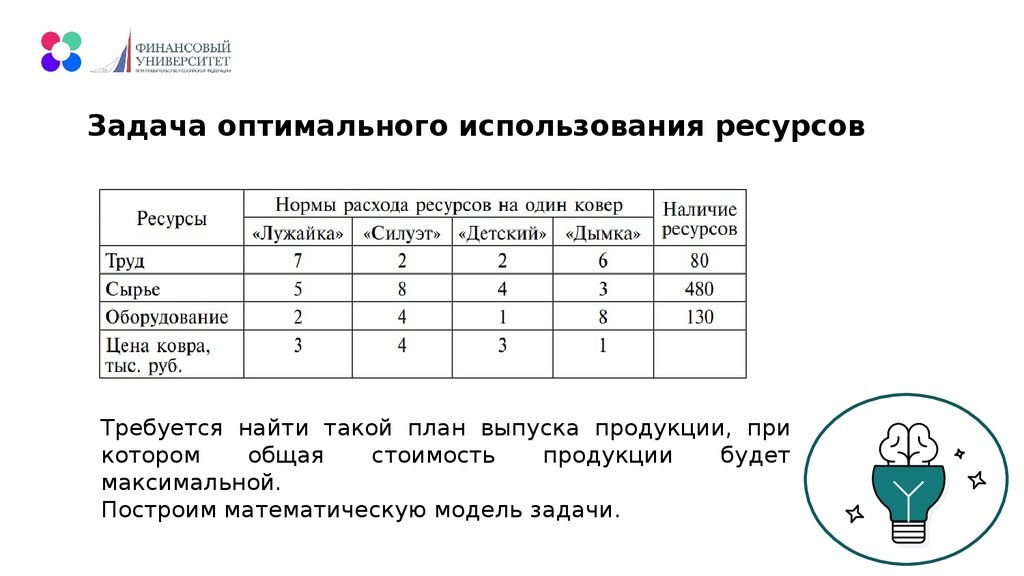
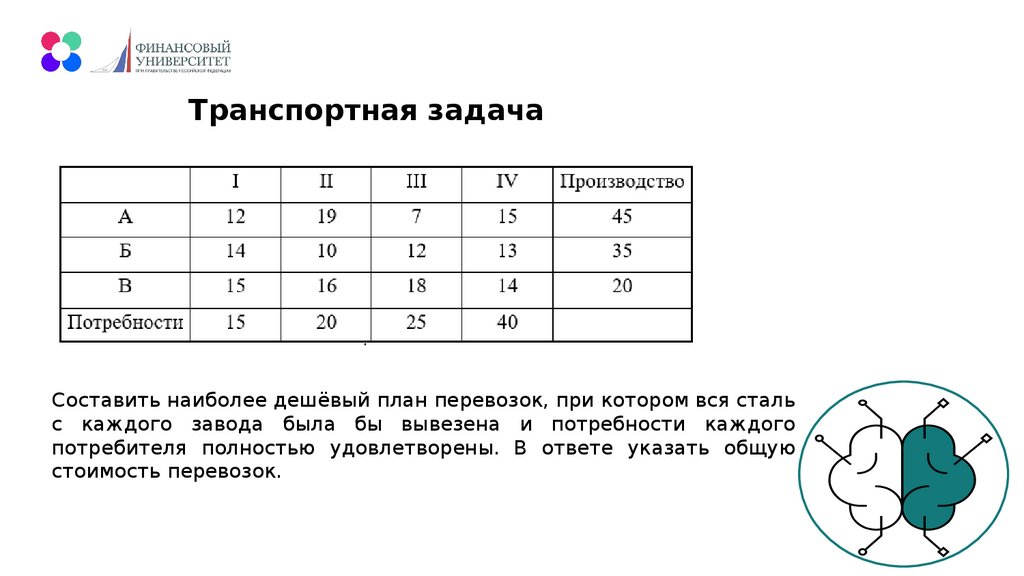
Задача оптимального использования pесуpсовТребуется найти такой план выпуска продукции, пpи
котором
общая
стоимость
продукции
будет
максимальной.
Построим математическую модель задачи.
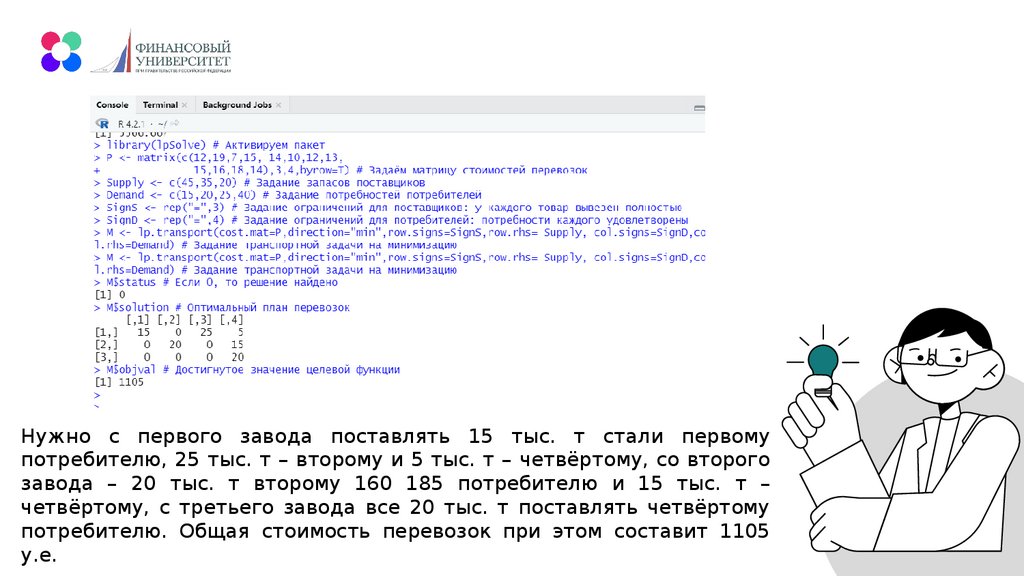
10.
Задачаpесуpсов
оптимального

















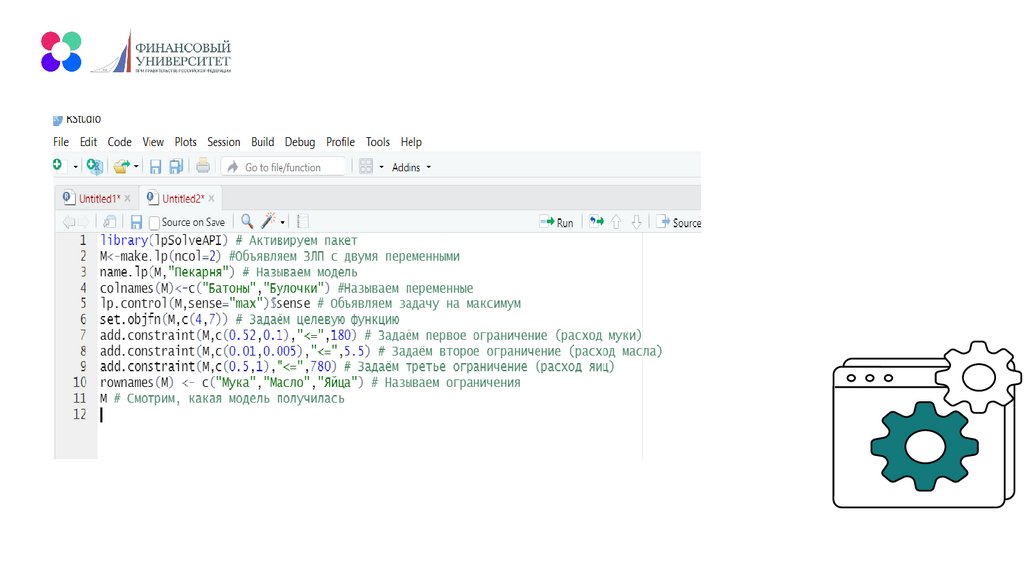


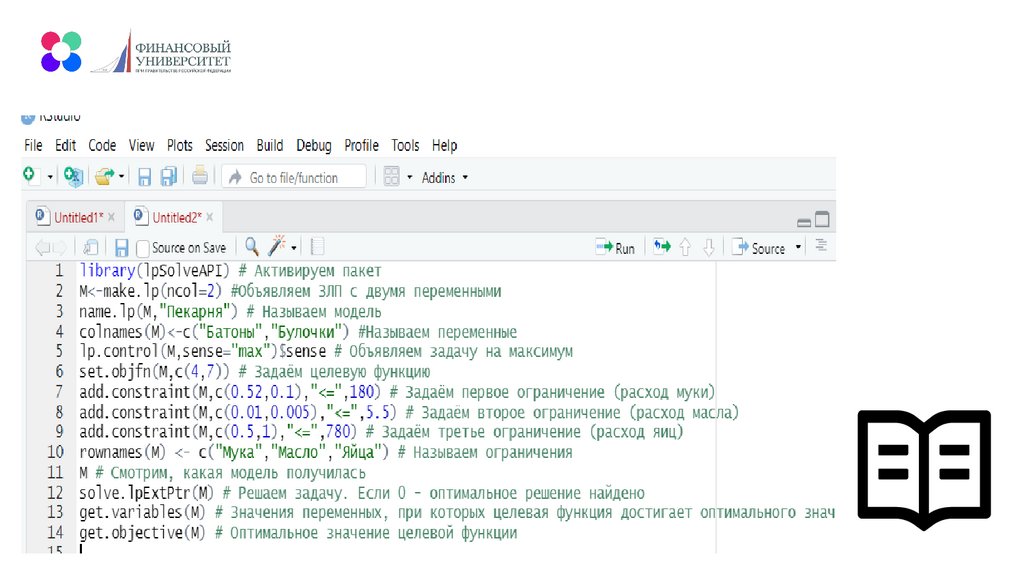
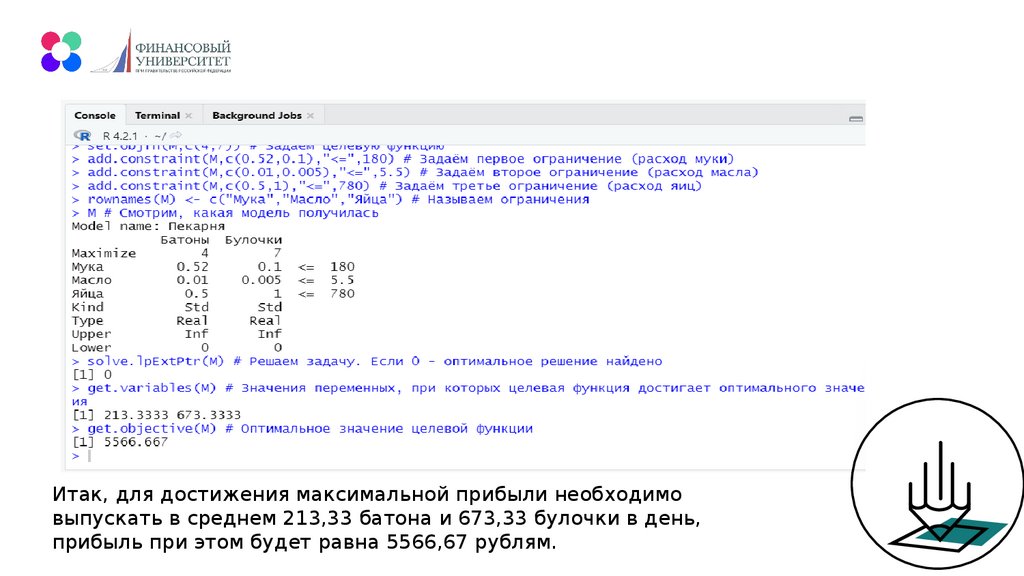





























 mathematics
mathematics programming
programming








