Similar presentations:
Математическое программирование (лекция1)
1.
О математическом программированииМатематическое программирование используется в
нефтяной индустрии, а также в сфере логистики,
планирования, составления расписаний.
Вообразим, что вы занимаетесь продажей жестяных
листов. Один клиент заказал у вас 70 листов, а
второй — 30 листов. При этом ваши запасы
хранятся на разных складах, на каждом из которых
осталось меньше 100 листов. Ваша задача —
минимизировать расходы на доставку жести
клиентам.
2.
Почему идеальные решения не всегдасамые комфортные?
3.
Общая формулировка задачиматематического программирования
Математическое программирование – это раздел
высшей математики, посвященный решению задач,
связанных с нахождением экстремумов функций
нескольких переменных, при наличии ограничений
на переменные.
Методами математического программирования
решаются задачи о распределении ресурсов,
планировании
выпуска
продукции,
ценообразования, транспортные задачи и т.д.
Построение математической модели экономической
задачи включает следующие этапы:
1. Выбор переменных задачи
2. Составление системных ограничений
3. Выбор целевой функции
4.
Общая формулировка задачиматематического программирования
Переменными задачи называются величины x1, x2, x3, …,
xn которые полностью характеризуют экономический
процесс.
Их обычно записывают в виде вектора X=(x1, x2, x3, …, xn)
Система ограничений включает в себя систему уравнений
и неравенств, которым удовлетворяют переменные задачи
и которые следуют из ограниченности ресурсов или
других
экономических
или
физических
условий,
например, положительности переменных и т. п.
Целевой функцией называют функцию переменных
задачи, которая характеризует качество выполнения
задачи, и экстремум которой требуется найти.
5.
6.
Общая формулировка задачиматематического программирования
Найти минимум или максимум целевой функции
F(x)=F(x1, x2, x3, …, xn)
При ограничениях
1(x1, x2, x3, …, xn){≤,=,≥}b1
2(x1, x2, x3, …, xn){≤,=,≥}b2
………
m(x1, x2, x3, …, xn){≤,=,≥}bm
X(x1, x2, x3, …, xn) – допустимое решение, если
выполняются ограничения.
Допустимое решение, при котором целевая
функция
достигает
оптимального
значения,
называется оптимальным планом
7.
Принципы классификации задачматематического программирования
По характеру
взаимосвязи между
переменными:
• Линейные
• Нелинейные
По характеру
изменения
переменных:
• Непрерывные
• Дискретные
По учету фактора
времени:
• Статические
• Динамические
По наличию информации о
переменных:
• Задачи в условиях
полной определённости
• Задачи в условиях
неполной информации
• Задачи в условиях
неопределенности
По числу критериев оценки
альтернатив:
• Простые однокритериальные
задачи
• Сложные
многокритериальные задачи
8.
ЗЗадачаАДАЧА линейного
ЛИНЕЙНОГО программирования
ПРОГРАММИРОВАНИЯ
Найти минимум или максимум целевой функции
max(min) f ( X ) c1 x1 c2 x2 cn xn
При функциональных ограничениях
a11 x1 a12 x2 a1n xn , , b1
a21x1 a22 x2 a2n xn , , b2
am1x1 am2 x2 amnxn , , bm
и прямых ограничениях
x j 0; j 1, n
9.
ЗАДАЧАлинейногоЛИНЕЙНОГО программирования
ПРОГРАММИРОВАНИЯ
Задача
В случае, когда все ограничения являются уравнениями и
все переменные удовлетворяют условию неотрицательности,
задачу линейного программирования называют канонической.
Z ( X ) c1 x1 c2 x2 cn xn max min
a11 x1 a12 x2 a1n xn b1
a x a x a x b
m1 1 m 2 2
mn n
m
xi 0, i 1,2, , n
n
n
aij xi b j
i 1
Z ( X ) ci xi max min
i 1
j 1,2, , m
xi 0, i 1,2, , n
10.
ЗАДАЧА линейногоЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача
программирования
Каноническая задача линейного программирования в
векторной форме
Z ( X ) C X max (min),
A1 x1 A2 x2 An xn A0
X 0
В данном случае введены векторы
X x1 , x 2 , , x n
a1i
a2 i
Ai , i 1,2, , n
ami
C c1 , c 2 , , c n
b1
b2
A0
bm
0 (0,0, ,0)
11.
ЗАДАЧАлинейногоЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача
программирования
Каноническая задача линейного программирования в
матричной форме записи имеет вид
Z ( X ) C X max (min),
AX A0
a11
a21
A
am1
X
a12 a1n
a22 a2 n
,
am 2 amn
x1
x2
X
xn
C c1 , c 2 , , c n
b1
b2
A0
bm
12.
ЗАДАЧАлинейногоЛИНЕЙНОГО программирования
ПРОГРАММИРОВАНИЯ
Задача
Приведение общей задачи линейного
программирования к канонической форме.
a1 x1 a 2 x2 ... a n xn b
a1 x1 a 2 x 2 ... a n x n x n 1 b
xn 1 b a1 x1 a2 x2 ... an xn
xn 1 0 - дополнительная переменная
13.
Решение системы линейных уравненийметодом Жордана-Гаусса
Элементарные преобразования системы (или
расширенной матрицы)
• Перестановка любых двух уравнений;
• Умножение обеих частей одного из уравнений
на любое отличное от нуля число;
• Прибавление к обеим частям одного и
уравнения соответствующих частей другого,
умноженных на любое число отличное от нуля;
• Вычеркивание нулевой строки (уравнения с
нулевым коэффициентом и своборным членом,
равным нулю)
14.
Решениесистемы
уравнений
Решение
системылинейных
линейных уравнений
методом
методомЖордана-Гаусса
Жордана-Гаусса
Элементарными преобразованиями расширенная матрица совместной
системы, имеющей бесчисленное множество решений, приводится к виду:
1
0
0
a1r 1
0
1
0
a 2 r 1
a1n b1
a 2 n b2
a rr 1
a rn br
0
0
1
Общее решение системы можно записать в виде:
x1 b1 a1r 1 xr 1 a1n xn
x2 b2 a2 r 1 xr 1 a2 n xn
xr br arr 1 xr 1 arn xn
15.
Двойственнаязадача
ДВОЙСТВЕННАЯ ЗАДАЧА
линейного
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
Прямая задача
Двойственная задача
n
Z ( X ) ci xi max min F (Y ) m b y min max
j j
i 1
n
j 1
m
aij xi b j j 1,2, , m
aij y j ci i 1,2, , n
i 1
j 1
x i 0 , i 1, 2 , , n
y j 0, j 1,2, , m
y j - объективно обусловленные оценки
16.
ДвойственнаяДВОЙСТВЕННАЯзадача
ЗАДАЧА
линейного
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
Правила составления двойственной задачи:
1. целевая функция исходной задачи формулируется на
максимум, а целевая функция двойственной задачи
- на минимум, при этом в задаче на максимум все
неравенства в функциональных ограничениях
имеют вид , а в задаче на минимум - вид ;
17.
Двойственнаязадача
ДВОЙСТВЕННАЯ ЗАДАЧА
линейного
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
Правила составления двойственной задачи:
2. матрица A составленная из коэффициентов при неизвестных
в системе ограничений исходной задачи, и аналогичная
матрица A* в двойственной задаче получаются друг из
друга транспонированием;
a11 a12
a21 a22
A
am1 am 2
a1n
a11
a2 n
a21
*
T
, A A
amn
an1
a12
a22
an 2
a1m
a2 m
anm
18.
Двойственнаязадача
ДВОЙСТВЕННАЯ ЗАДАЧА
линейного
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
Правила составления двойственной задачи:
3. Число переменных в двойственной задаче равно числу
функциональных ограничений исходной задачи, а
число ограничений в системе двойственной задачи числу переменных в исходной задаче;
4. Коэффициентами при неизвестных в целевой функции
двойственной задачи являются свободные члены в
системе ограничений исходной задачи, а правыми
частями в ограничениях двойственной задачи коэффициенты при неизвестных в целевой функции
исходной задачи;
19.
ДВОЙСТВЕННАЯ ЗАДАЧАДвойственная
задача
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
линейного
Правила составления двойственной задачи:
5. Каждому ограничению одной задачи соответствует
переменная другой задачи: номер переменной совпадает
с номером ограничения; при этом ограничению,
записанному в виде неравенства , соответствует
переменная, связанная условием неотрицательности.
Если функциональное ограничение исходной задачи
является равенством, то соответствующая переменная
двойственной задачи может принимать как
положительные, так и отрицательные значения.
20.
ДвойственнаяДВОЙСТВЕННАЯзадача
ЗАДАЧА
линейного
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
Математические модели пары двойственных задач могут
быть симметричными и несимметричными. В
несимметричных двойственных задачах система
ограничений исходной задачи задается в виде равенств, а
двойственной - в виде неравенств, причем переменные в
двойственной задаче могут быть и отрицательными. В
симметричных двойственных задачах система ограничений
как исходной, так и двойственной задачи задается в виде
неравенств, причем на двойственные переменные
налагается условие неотрицательности.
21.
ДВОЙСТВЕННАЯ ЗАДАЧАДвойственная
задача
ЛИНЕЙНОГОпрограммирования
ПРОГРАММИРОВАНИЯ
линейного
Исходная задача
Двойственная задача
Симметричные пары
Z ( X ) C X max ,
AX A0
YAT C
X
Y
Z ( X ) C X min ,
F (Y ) Y A0 max,
AX A0
YAT C
Y
X
F (Y ) Y A0 min,
22.
Графическое решение ЗАДАЧИ ЛПГрафический метод решения задачи ЛП состоит из 2 этапов:
1) построение
пространства
допустимых
решений,
удовлетворяющих всем ограничениям модели;
2) нахождение оптимального решения среди всех точек
пространства допустимых решений.
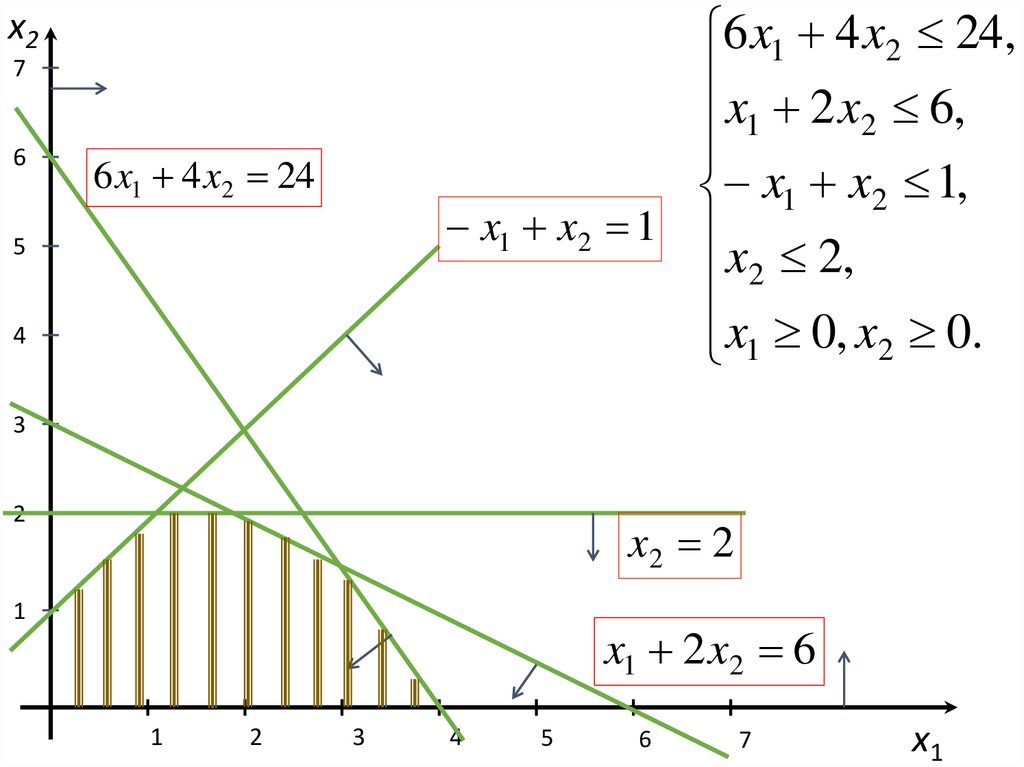
Изучение рынка сбыта показало, что суточный спрос на синюю краску никогда не
превышает спроса на краску черную более, чем на 1 т. Кроме того, установлено, что
спрос на синюю краску никогда не превышает 2 т в сутки.
Расход сырья (в тоннах) на
тонну краски
Максимально
возможный
ежедневный
расход сырья
Черная
Синяя
Сырье М1
6
4
24
Сырье М2
1
2
6
Доход (в
1000$) на
тонну краски
5
4
23.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬХ1 – ежедневный объем производства черной краски
Х2 – ежедневный объем производства синей краски
Z = 5x1 + 4x2 → max.
6 x1 4 x2 24,
x 2 x 6,
2
1
x1 x2 1,
x 2,
2
x1 0, x2 0.
Изучение рынка сбыта
показало, что суточный
спрос на синюю краску
никогда не превышает
спроса на черную краску
более, чем на 1 т. Кроме
того, установлено, что
спрос на синюю краску
никогда не превышает 2 т в
сутки.
24.
6 x1 4 x2 24,x 2 x 6,
2
1
x1 x2 1,
x1 x2 1
x2 2,
x1 0, x2 0.
х2
7
6
6 x1 4 x2 24
5
4
3
2
x2 2
1
x1 2 x2 6
1
2
3
4
5
6
7
х1
25.
х2Z 5 x1 4 x2 max .
Z = 5х1 + 4х2 = 15
x1 2 x2 6
3
Возрастание Z
2
E
D
x1 = 3 т.
x2 = 1,5 т.
Z = 21 000$
C
1
6 x1 4 x2 24,
x 2 x 6,
2
1
x1 x2 1,
x 2,
2
x1 0, x2 0.
F
6 x1 4 x2 24
Z = 5х1 + 4х2 = 10
A
B
1
2
3
4
х1
26.
ЗАДАЧАлинейногоЛИНЕЙНОГО программирования
ПРОГРАММИРОВАНИЯ
Задача
Алгоритм решения задачи линейного программирования
графическим методом таков:
1. Строится область допустимых решений;
2. Строится вектор нормали к линии уровня с точкой
приложении в начале координат
3. Перпендикулярно вектору нормали проводится одна из
линий уровня, проходящая через начало координат.
4. Линия уровня перемещается до положения опорной
прямой. На этой прямой и будут находиться максимум или
минимум функции.
В зависимости от вида области допустимых решений и
целевой функции задача может иметь единственное решение,
бесконечное множество решений или не иметь ни одного
оптимального решения.
27.
ЗАДАЧАлинейногоЛИНЕЙНОГО программирования
ПРОГРАММИРОВАНИЯ
Задача
x2
A
x2
A
Z max
Z min
c ( c1 , c 2 )
0
B
c
x1
Z 1 c1 x1 c 2 x 2 0
0
Z 0
B
Z max
x1
Если прямая функции параллельна отрезку [АВ], принадлежащему области
допустимых решений, то максимум функции Z достигается в точке А и в точке В, а ,
следовательно, и в любой точке отрезка [АВ], т.к. эти точки могут быть выражены
в виде линейной комбинации угловых точек А и В.
28.
ЗАДАЧАлинейногоЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задача
программирования
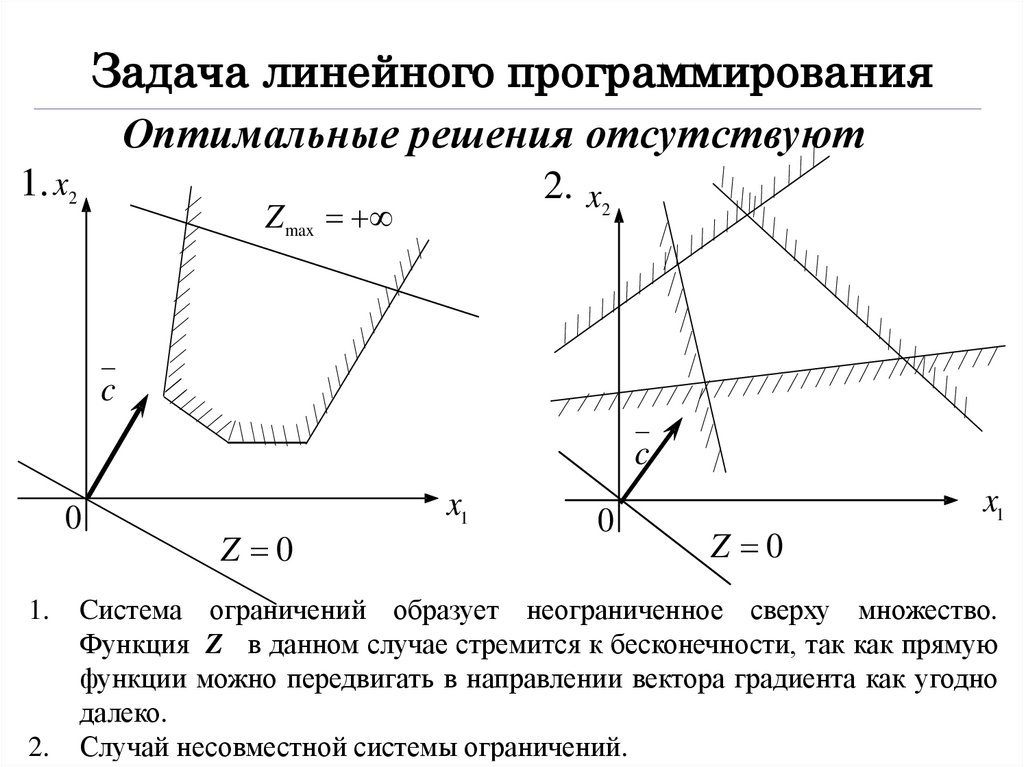
Оптимальные решения отсутствуют
1. x2
2. x2
Z max
c
c
0
1.
2.
Z 0
x1
0
Z 0
x1
Cистема ограничений образует неограниченное сверху множество.
Функция Z в данном случае стремится к бесконечности, так как прямую
функции можно передвигать в направлении вектора градиента как угодно
далеко.
Случай несовместной системы ограничений.


























 mathematics
mathematics








