Similar presentations:
Двойственность в линейном программировании
1. Двойственность в линейном программировании
2.
Пусть прямая задача, состоит в нахождениимаксимального значения функции:
F c1 x1 c2 x2 cn xn
При условиях
a11 x1 a12 x2 a1n xn b1
a21 x1 a22 x2 a2 n xn b2
akn xn bk
ak 1 x1 ak 2 x2
ak 1n xn bk 1
ak 11 x1 ak 12 x2
am1 x1 am 2 x2 amn xn bm
x j 0 j 1n
3.
Тогда двойственной по отношению к прямой задаченазывается задача нахождения минимума функции
'
F b y b y b y
1
При условиях
1
2
m
2
m
a11 y a21 y am1 y c1
1
2
m
y y am 2 ym c2
a12 1 a22 2
aml ym cl
a1l y1 a2 l y2
a1l 1 y1 a2 l 2 y2 aml 1 ym cl 1
a
a
a
cn
1 n y1
2 n y2
mn y m
0 i 1,n
yi
4. Правила формирования двойственной задачи :
Целевая функция исходной задачиисследуется на максимум, а целевая
функция двойственной задачи
на
минимум
5.
Матрицаa11 a12 a1n
из коэффициентов при
a 21 a 22 a 2n неизвестных в системе
A
,
ограничений прямой задачи
a m1 a m 2 a mn
a
11 a 21 a m1
и аналогичная
am2
матрица
T a12 a 22
A
a1n a 2n a mn
в двойственной задаче
получаются друг из друга
транспонированием.
6.
Число ограничений одной из задачсовпадает с числом переменных в другой
задаче.
Коэффициенты при переменных в
целевой функции одной задачи являются
свободными
членами
системы
ограничений в другой.
7.
Если переменная xj исходной задачиможет
принимать только неотрицательные значения, то jе ограничение двойственной задачи является
неравенством вида “ ”.
Если
переменная xj может принимать как
положительные, так и отрицательные значения,
то j-е ограничение двойственной задачи уравнение.
Аналогично, если i-е ограничение в системе
исходной задачи является неравенством, то yi 0.
Если же i-е ограничение есть уравнение, то
переменная
yi
может
принимать
как
положительные, так и отрицательные значения.
8. Алгоритм составления двойственной задачи:
Привести все неравенства системы ограниченийисходной задачи к одному виду: если в исходной
задаче ищут максимум линейной функции, то
все неравенства системы ограничений привести
к виду “ ”, а если минимум – к виду “ ”.
Для этого неравенства, в которых данное
требование не выполняется, умножить на –1.
9.
Составить расширенную матрицусистемы ограничений исходной задачи, в
которую включить
матрицу коэффициентов при переменных ,
столбец свободных членов
и строку коэффициентов при переменных
в линейной функции.
10.
Найти матрицу А Т транспонированную кматрице А
Сформулировать двойственную задачу на
основании полученной матрицы и
условия неотрицательности переменных.
11. Пример. Составить задачу, двойственную к следующей задаче:
F x1 2 x2 max2 x1 x2 1
4 24
x1 x2
x1 x2 3
x1 0, x2 0
12.
Так как исходная задача на максимизацию, топриведем все неравенства системы ограничений
к виду “ ”, для этого обе части первого
неравенства умножим на –1. Получим:
2 x1 x2 1
4 24
x1 x2
x
1 x2 3
x1 0, x2 0
13. Составим расширенную матрицу системы:
2 11 4
A1
1 1
1 2
1
24
3
F
14. Найдем матрицу А т, транспонирующую к А.
2 1 1 1T
1
4
1
2
A1
1 24 3 F'
15. Сформулируем двойственную задачу:
'F y1 24 y 2 3 y3 min
2 y y y 1
1
2
3
y1 4 y 2 y 3 2
y 0, y 0
3
1
16. Свойства двойственных задач
Теорема 1. Если исходная задача имеетоптимальный план, то и сопряженная к ней
задача имеет оптимальный план, причем
значение ЦФ при этих планах совпадают.
Если ЦФ одной из двойственных задач не
ограничена на множестве допустимых решений
(для исходной – сверху, для сопряженной –снизу),
то двойственная задача вообще не имеет плана.
17.
Теорема 2 . Пара допустимых решений X* - висходной задаче, Y* - в двойственной задаче
будут оптимальными решениями тогда и только
тогда,
кода
выполняются
следующие
соотношения:
n
( aij x j bi ) y * i 0 i 1, m
*
j 1
m
( aij y * i c j ) x * j 0
i 1
j 1, n
18. Связь исходной и двойственной задач
Решение одной из них может быть получено изрешения другой.
Используя последнюю симплекс-таблицу, можно
найти оптимальный план двойственной задачи.
Компоненты оптимального плана двойственной
задачи совпадают с элементами m+1-й строки
столбцов единичных векторов первоначального
базиса, если данный коэффициент cj=0, и равны
сумме соответствующего элемента этой строки и cj,
если cj>0.
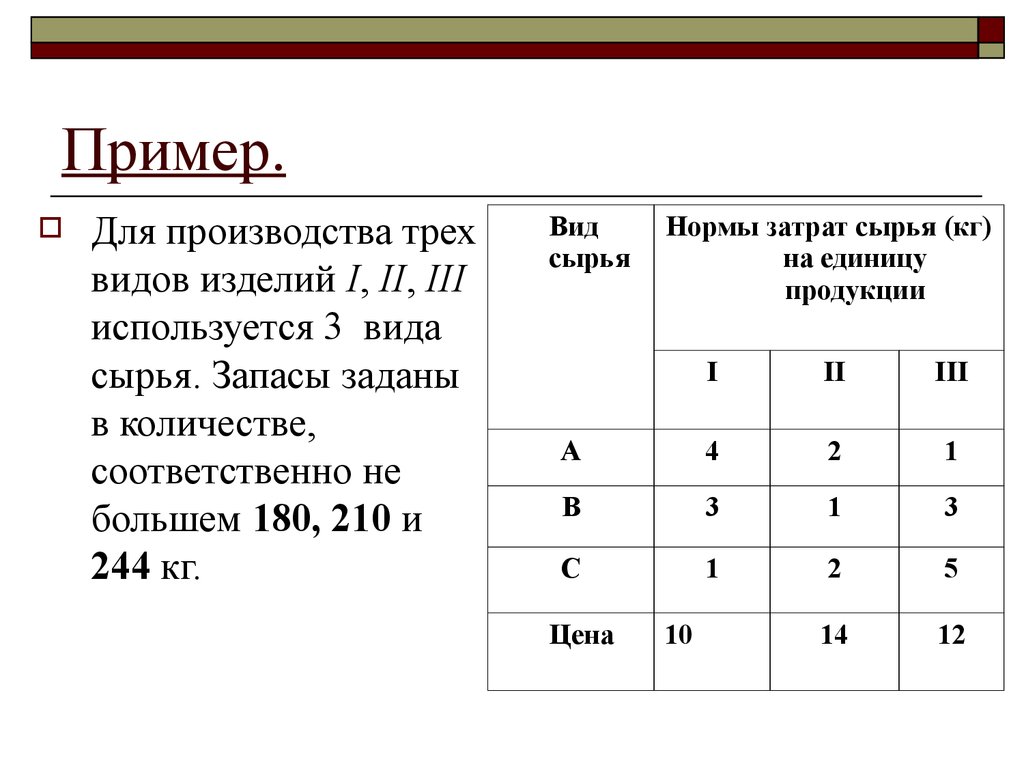
19. Пример.
Для производства трехвидов изделий I, II, III
используется 3 вида
сырья. Запасы заданы
в количестве,
соответственно не
большем 180, 210 и
244 кг.
Вид
сырья
Нормы затрат сырья (кг)
на единицу
продукции
I
II
III
A
4
2
1
B
3
1
3
C
1
2
5
14
12
Цена
10
20.
Определить план выпуска продукции, прикотором обеспечивается её максимальная
стоимость и оценить каждый из видов сырья,
используемых для производства продукции.
Оценки, приписываемые каждому из видов сырья,
должны быть такими,
чтобы оценка всего используемого сырья была
минимальной,
а суммарная оценка сырья, используемого на
производство единицы продукции каждого вида, не меньше цены единицы продукции данного вида.
21. Решение.
Обозначим через x1 – количество изделий I,x2 – изделий II, x3 – изделий III,
запланированных к производству.
Тогда нужно решить задачу
F 10 x 14 x 12 x max
1
2
3
4 x1 2 x2 x3 180
3 210
x1 x2 3x3
x1 2 x2 5x3 244
x1, x2, x3 0
22.
Припишем каждому из видов сырья, используемыхдля производства продукции, двойственную оценку,
равную yi .
Тогда общая оценка сырья, используемого на
производстве продукции составит:
'
F 180 y1 210 y 2 244 y3 min
23.
Двойственные оценки должны быть такими , чтобыобщая оценка сырья, используемого на производство
единицы продукции каждого вида, была не меньше
цены единицы продукции данного вида, то есть
должны удовлетворять следующей системе неравенств
4 y 3 y y 10
1
2
3
2 y1 y 2 2 y 3 14
12
y
3
y
5
y
1
2
3
y1 , y 2 , y 3 0
24.
Эти задачи образуют пару двойственныхзадач.
Решение прямой задачи дает оптимальный
план производства изделий I, II, III,
Решение двойственной - оптимальную
систему оценок сырья, используемого для
производства этих изделий.
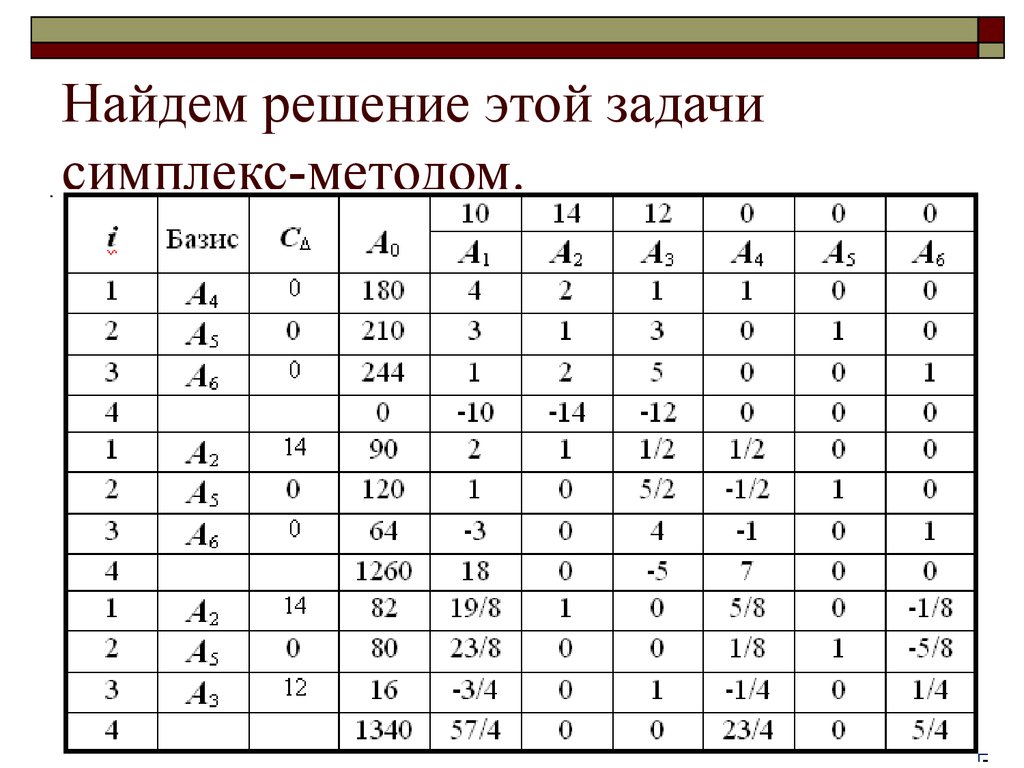
25. Найдем решение этой задачи симплекс-методом.
26.
Из этой таблицы видно, что оптимальным планомпроизводства изделий I, II, III является такой, при
котором изготавливается 82 изделия II и 16
изделий III и остается не использованным 80 кг
сырья B,
а общая стоимость изделий равна 1340 руб.
Из этой таблицы также видно, что оптимальным
решением двойственной задачи является
y
1
23 4,
y
2
0,
y
3
5 4.
27. Положительную двойственную оценку имеют те виды сырья, которые полностью используются.
Переменные y1 и y3 обозначают двойственныеоценки сырья видов A и C.
Эти оценки отличны от нуля, и сырье видов
А и С используются полностью.
Двойственная оценка сырья вида В y2=0.
Этот вид сырья используется не полностью.
28. Вычислим значение целевой функции двойственной задачи
' 180 23 4 210 0 244 5 4 1340F
Первая теорема двойственности выполняется –
значение
целевых
функций
двух
задач
получилось равным
29. Проверим вторую терему двойственности
Сначала подставим полученные значения переменных вограничения прямой задачи, вычтем свободные члены и
умножим ограничения на двойственные оценки. Должны
получиться нули
(4 0 2 82 16-180) 23 / 4 0
(3 0
82 3 16 210) 0 0
(0 2 82 5 16 244) 5 / 4 0
30.
Подставим значения двойственных оценокв ограничения двойственной задачи
(4 23 / 4 3 0 5/4-10) 0 0
(2 23 / 4
0 2 5 / 4 14) 82 0
( 23 / 4 3 0 5 5 / 4 12) 16 0
ИЛИ
23 5 4 10
23 2 5 2 14
23 4 25 4 12
31.
23 5 4 1023 2 5 2 14
23 4 25 4 12
Первое ограничение выполняется как строгое неравенство.
Это означает, что двойственная оценка сырья,
используемого на производство одного изделия типа I,
выше цены этого изделия и, следовательно, выпускать
изделие I невыгодно.
Второе и третье ограничения являются равенствами. Это
означает, что двойственные оценки сырья, используемого
на производство единицы изделий II и III равны их ценам.
Поэтому выпускать изделия этих двух видов экономически
целесообразно.
32. Вопросы
1.2.
3.
4.
5.
6.
Какую задачу называют двойственной?
Как формируется двойственная задача?
Как связаны виды ограничений и условия
неотрицательности переменных?
Первая теорема двойственности
Вторая теорема двойственности.
Как можно получить оптимальное решение
двойственно задачи из решения прямой?






























 mathematics
mathematics








