Математические модели в экономике

1. МАТЕМАТИЧЕСКИЕ МОДЕЛИ В ЭКОНОМИКЕ

2. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

Математическая модель - это способ
описания реальной жизненной ситуации
(задачи) с помощью математического языка.
Составить математическую модель - это
значит записать условие задачи в виде
совокупности (системы) уравнений,
неравенств, функций и т.д. в строгом
соответствии тексту задачи.

3. МАТЕМАТИЧЕСКИЕ МОДЕЛИ

1. Проанализировать явную, открытую
информацию задачи. Числа, значения и т.п.
2. Выявить скрытую информацию задачи.
Это текст, который предполагает наличие
дополнительных знаний .
3. Выявить связь данных между собой. Эта
связь может быть дана открытым текстом
(что-то равно чему-то), а может быть и
скрыта за простыми словами.

4. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Целевая функция
F c1 x1 c2 x2 c3 x3 ... cn xn max(min)
Система ограничений
a11 x1 a12 x2 a13 x3 ... a1n xn b1
a x a x a x ... a x b
21 1 22 2
23 3
2n n
2
...
am1 x1 am 2 x2 am 3 x3 ... amn xn bm

5. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ПРИМЕР. Фирма выпускает два вида
древесно-стружечных плит - обычные и
улучшенные. При этом производится две
основные операции - прессование и отделка.
Требуется указать, какое количество плит
каждого типа можно изготовить в течение
месяца так, чтобы обеспечить максимальную
прибыль при следующих ограничениях на
ресурсы (материал, время, затраты).

6. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

Партия из 100 плит
Затраты
улучшенн
обычных
ых
Имеющиеся
ресурсы на
месяц
Материал (усл.ед.)
Время на прессование
(часы)
Время на отделку (часы)
Средства (деньги)
3
5
55
1
5
70
5
2
60
45
60
1500
Прибыль
5
6

7. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

РЕШЕНИЕ. Пусть
x1 - количество партий обычных плит;
x2 - количество партий улучшенных плит.
Необходимые материалы
3x1 5x2 55
Материал (кв.м):
Время на прессование x1 5x2 45
Время на отделку 5x1 2x2 60
70x1 60x2 1500
Средства

8. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ

ЦЕЛЕВАЯ ФУНКЦИЯ (ПРИБЫЛЬ)
F ( X ) 5x1 6x2 max
Математическая модель:
F ( X ) 5x1 6x2 max
3 x1 5 x2 55
x 5 x 45
1
2
5 x1 2 x2 60
70 x1 60 x2 1500

9. ПРИМЕР

Известно, что содержание трех питательных веществ
А, В и С в рационе питания должно быть не менее
90, 70 и 90 единиц соответственно. Указанные
питательные вещества содержат два вида
продуктов. Содержание единиц питательных
веществ в одном килограмме каждого из видов
продуктов приведено в табице.
Цены 1 кг продуктов вида I и II соответственно равны
10 и 12-ти условным единицам. Определите
дневной рацион, обеспечивающий получение
необходимого количества питательных веществ,
при минимальных денежных затратах.

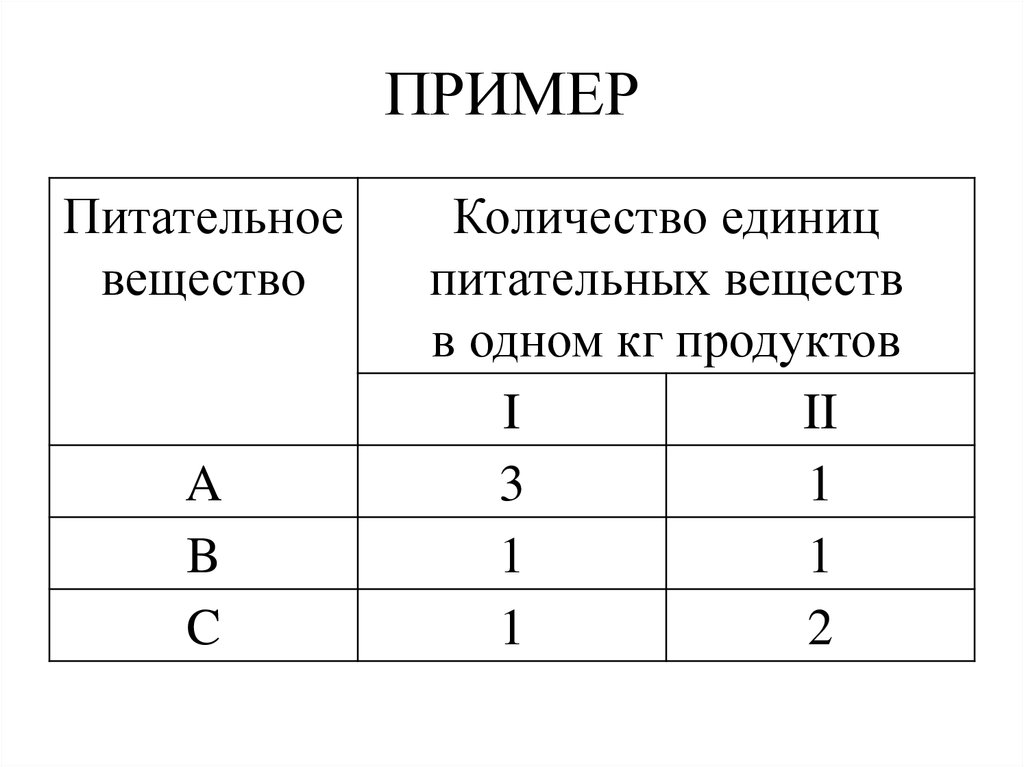
10. ПРИМЕР

Питательное
вещество
A
B
C
Количество единиц
питательных веществ
в одном кг продуктов
I
II
3
1
1
1
1
2

11. ПРИМЕР

РЕШЕНИЕ. Пусть
x1 – количество продукта I в рационе (в кг);
x2 – количество продукта II в рационе (в кг).
Целевая функция – стоимость рациона
F ( X ) 10 x1 12 x2 min

12. ПРИМЕР

Ограничения – условия на содержание
питательных веществ:
А:
3x1 x2 90
В:
x1 x2 70
С:
x1 2 x2 90

13. ПРИМЕР

Математическая модель:
F ( X ) 10 x1 12 x2 min
3x1 x2 90;
x1 x2 70;
x 2 x 90
2
1

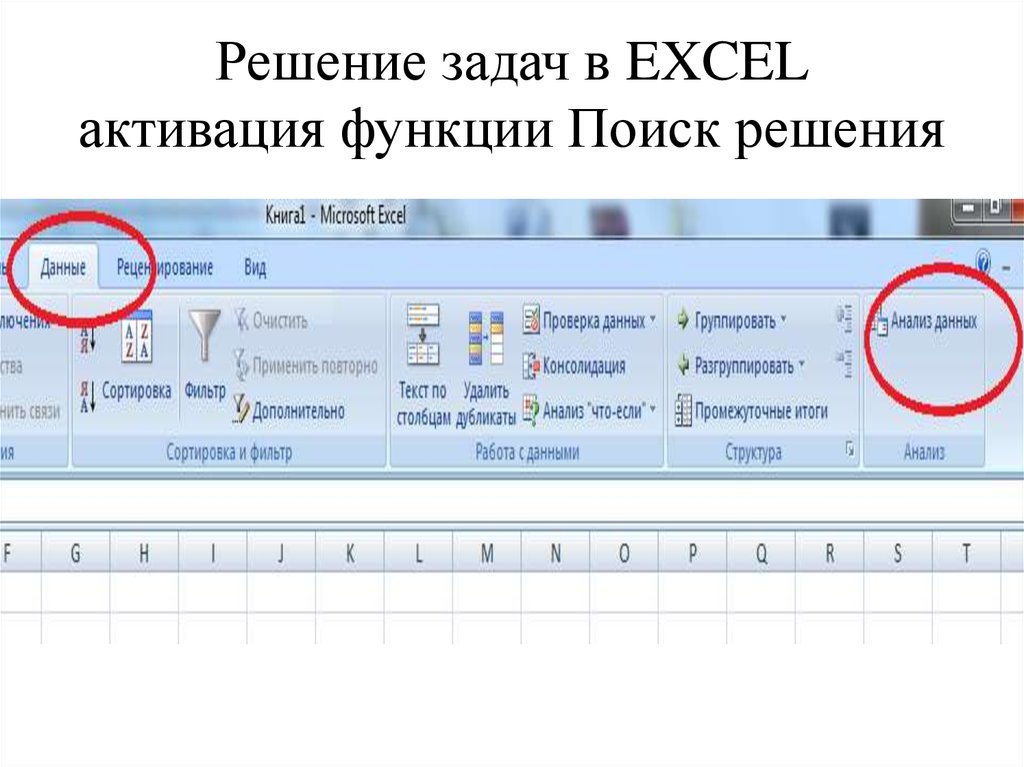
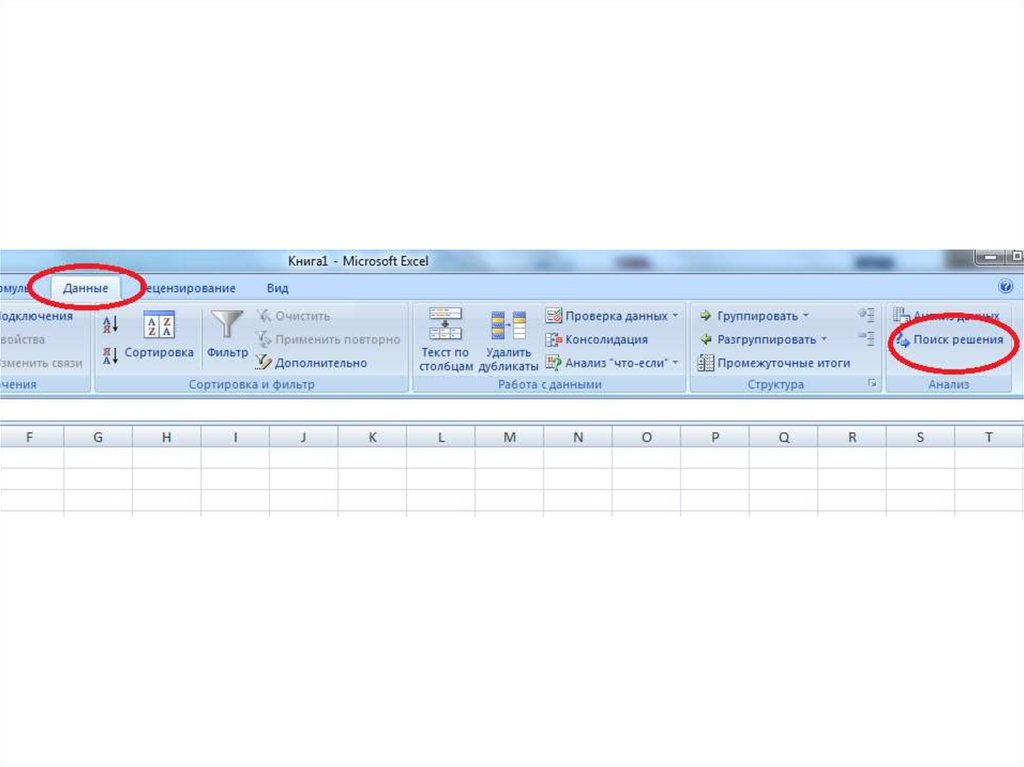
14. Решение задач в EXCEL

Активация функции Поиск решения.

15. Решение задач в EXCEL активация функции Поиск решения

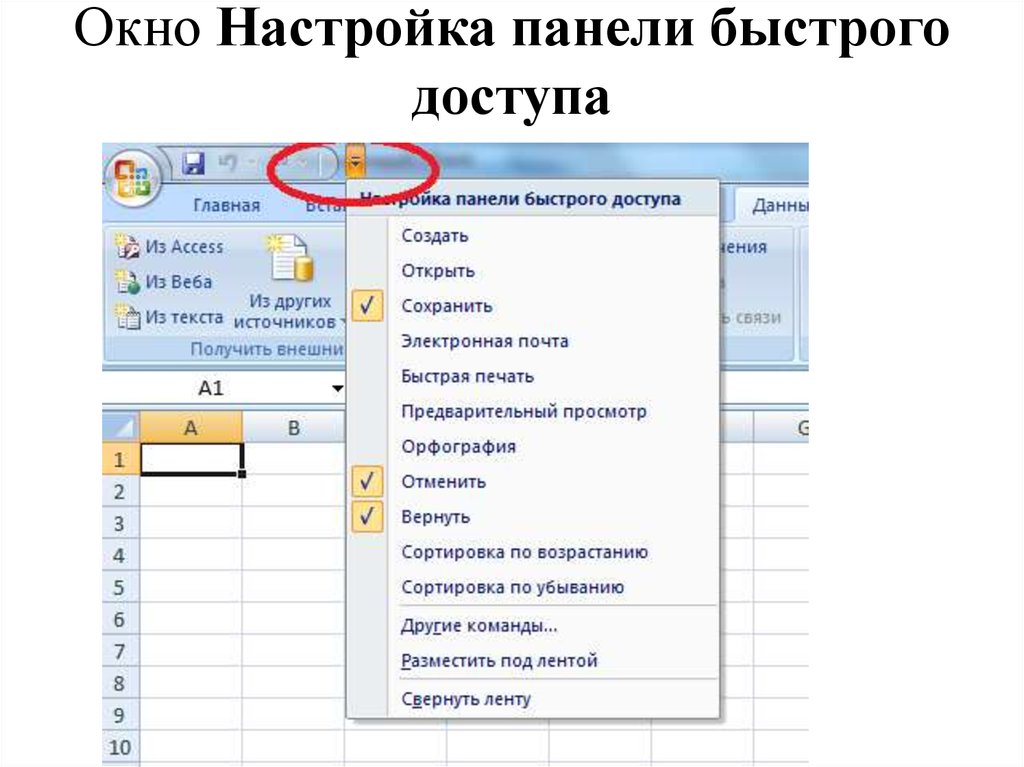
16. Окно Настройка панели быстрого доступа

17. Другие команды

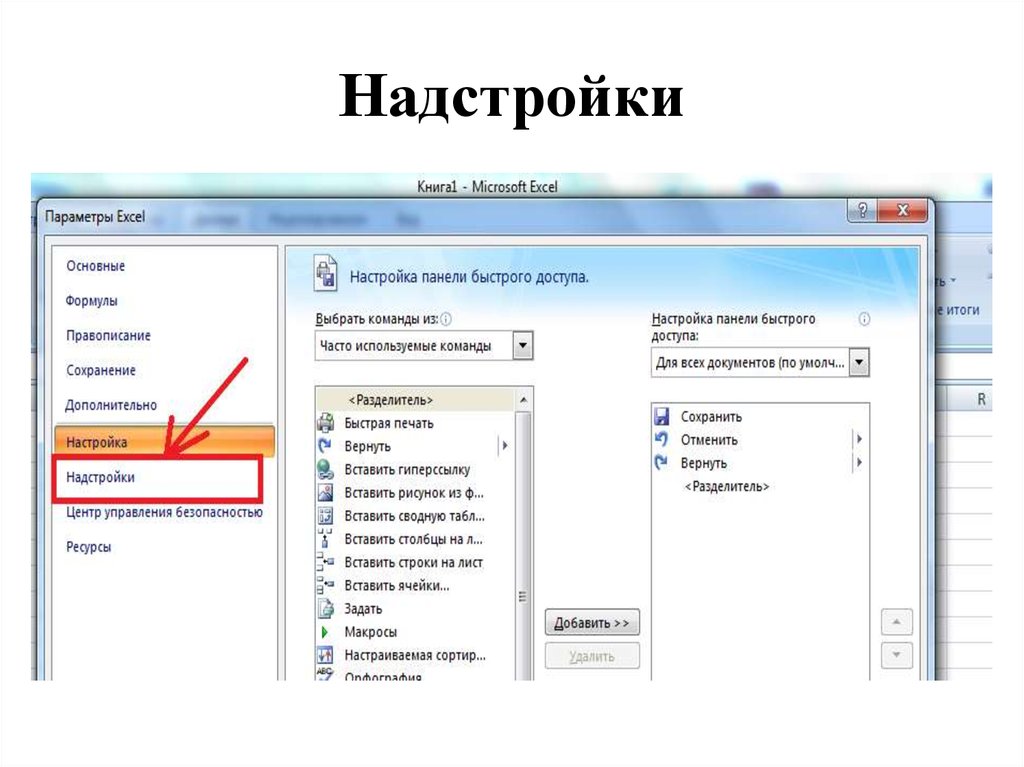
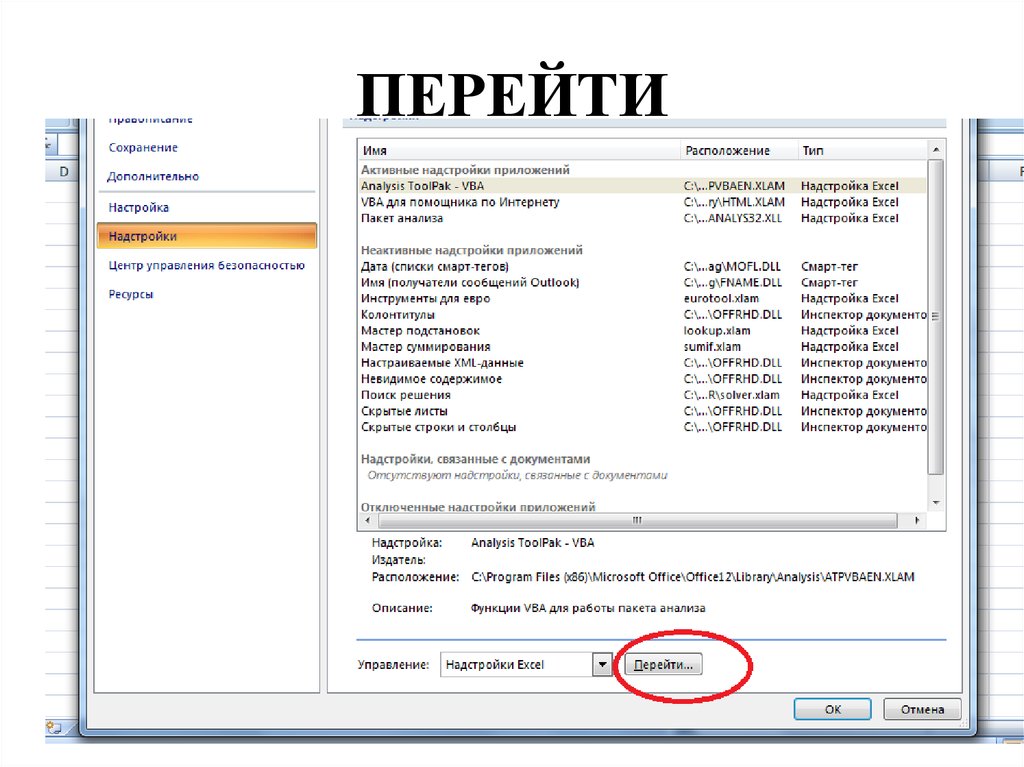
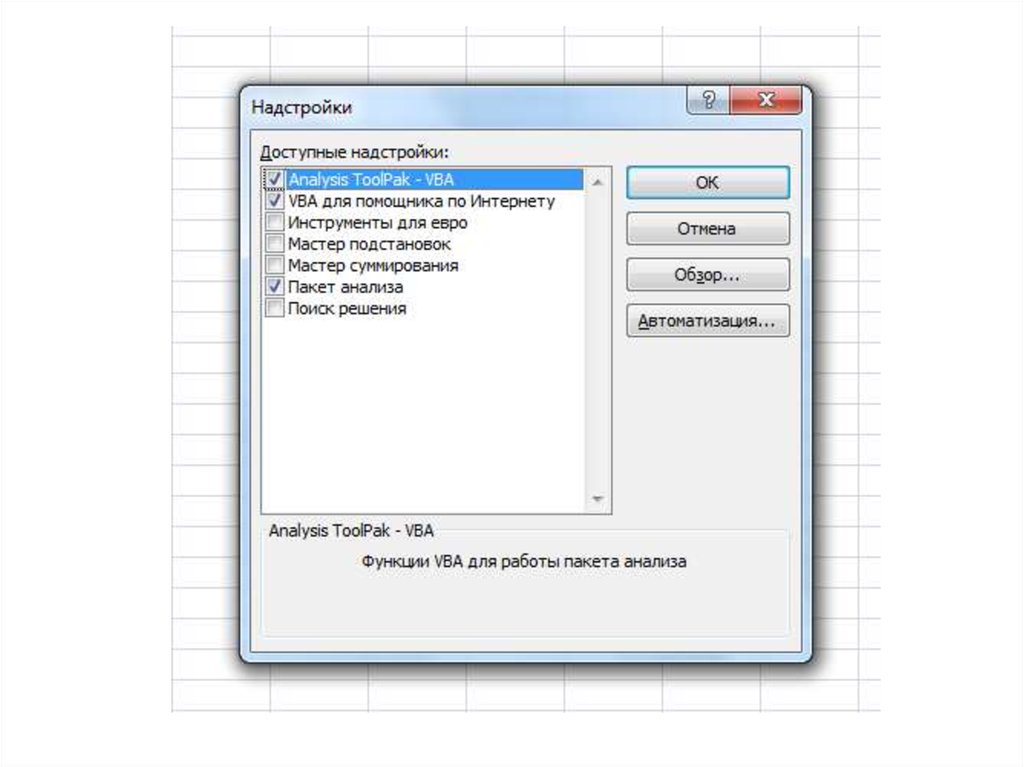
18. Надстройки

19. ПЕРЕЙТИ

20.

21. Поиск решения - ОК

22.

23. Введение данных: Резервируются ячейки неизвестных (переменных)

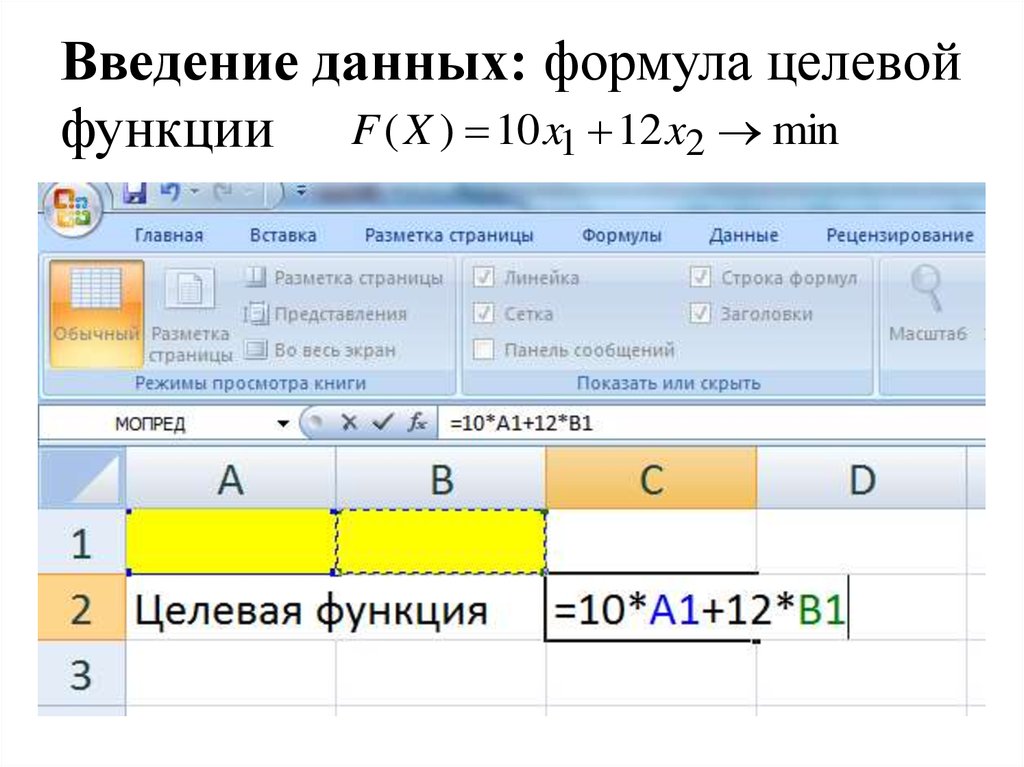
24. Введение данных: формула целевой функции

F ( X ) 10 x1 12 x2 min

25. Введение данных: формулы левых частей неравенств-ограничений

3x1 x2 90;
x1 x2 70;
x 2 x 90
2
1

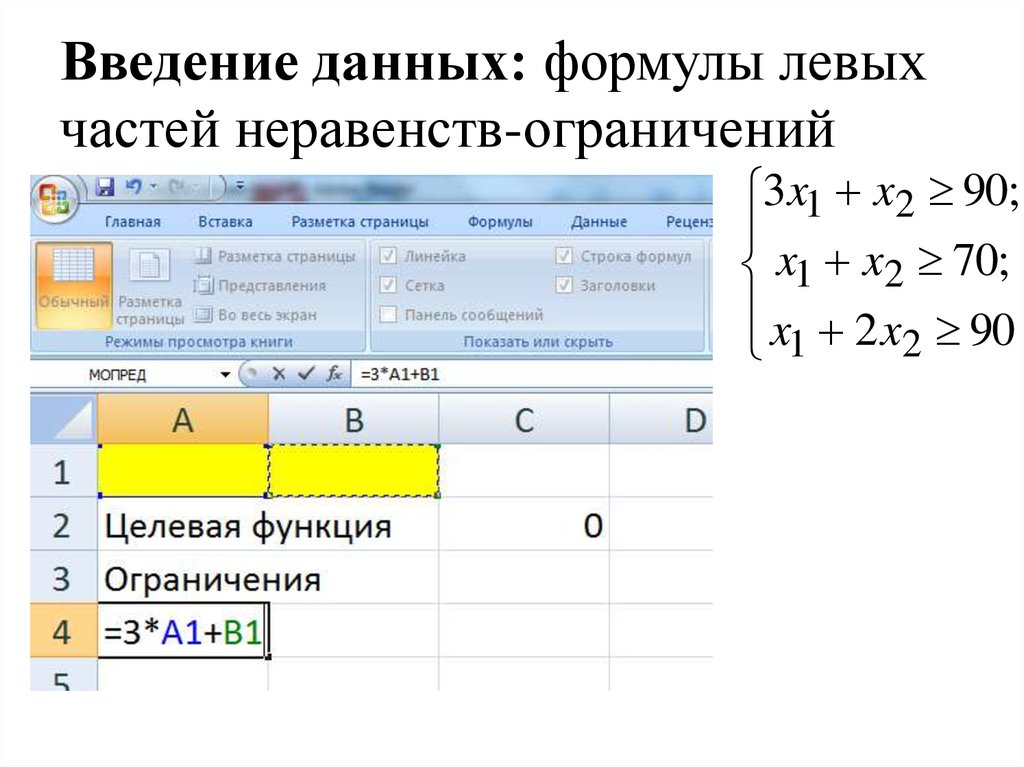
26. Введение данных: формулы левых частей неравенств-ограничений

3x1 x2 90;
x1 x2 70;
x 2 x 90
2
1

27. Введение данных: формулы левых частей неравенств-ограничений

3x1 x2 90;
x1 x2 70;
x 2 x 90
2
1

28. Введение данных: значения правых частей неравенств-ограничений

3x1 x2 90;
x1 x2 70;
x 2 x 90
2
1

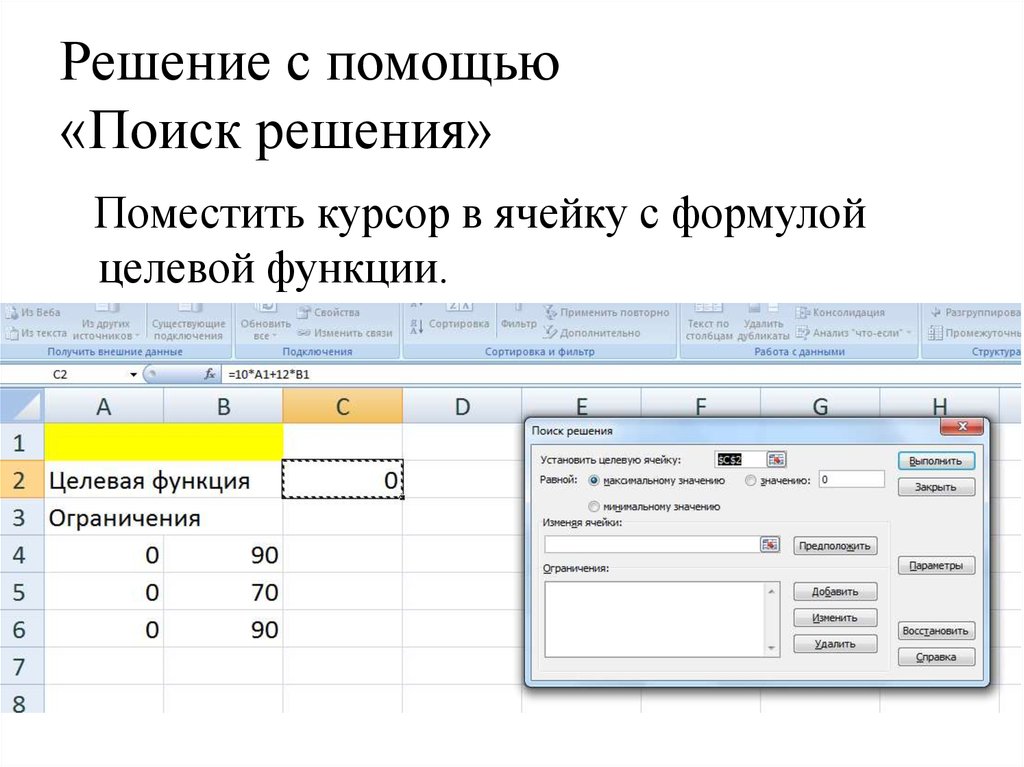
29. Решение с помощью «Поиск решения»

Поместить курсор в ячейку с формулой
целевой функции.
Данные – Поиск решения

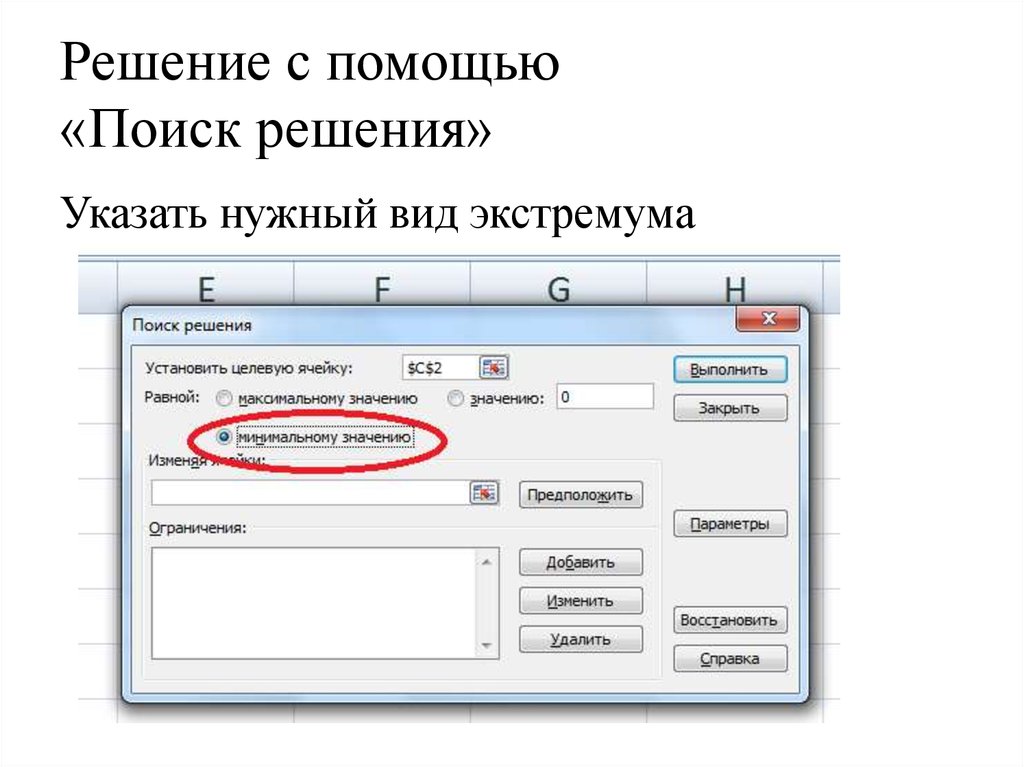
30. Решение с помощью «Поиск решения»

Указать нужный вид экстремума

31. Решение с помощью «Поиск решения»

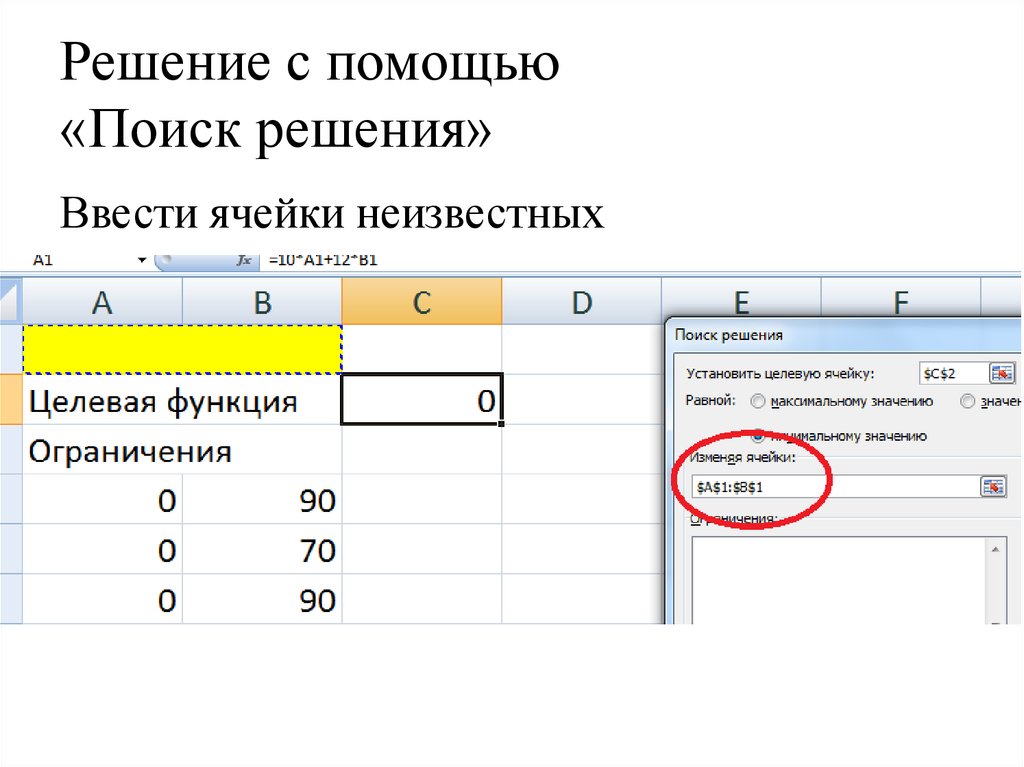
Ввести ячейки неизвестных

32. Решение с помощью «Поиск решения»

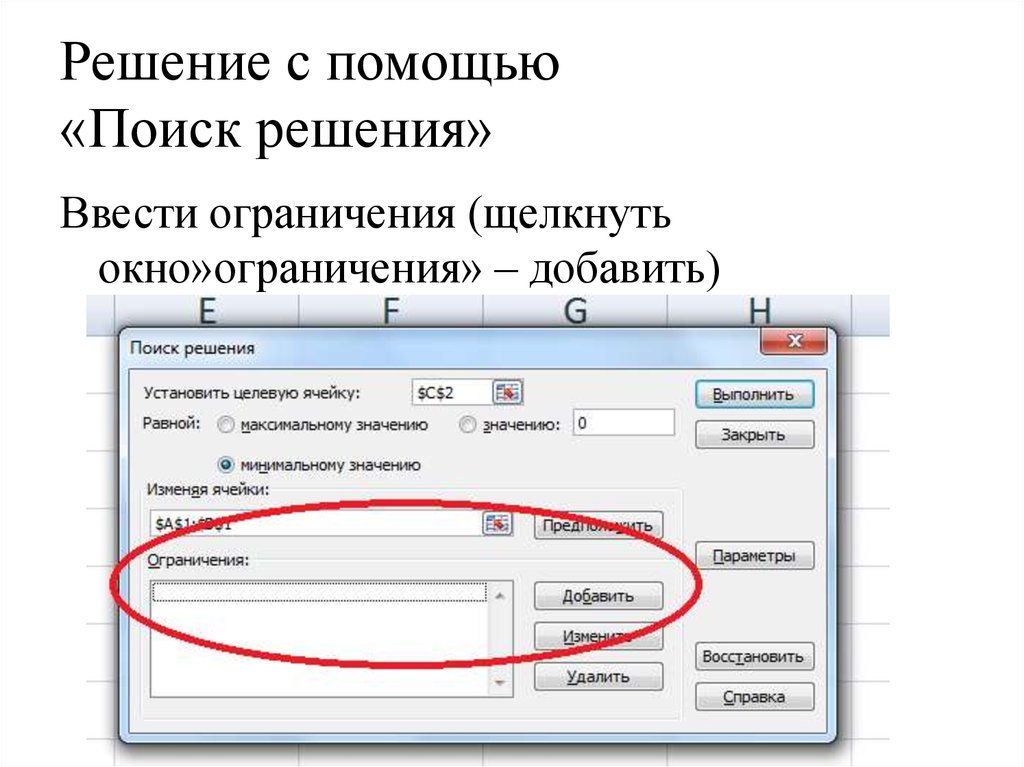
Ввести ограничения (щелкнуть
окно»ограничения» – добавить)

33. Решение с помощью «Поиск решения»

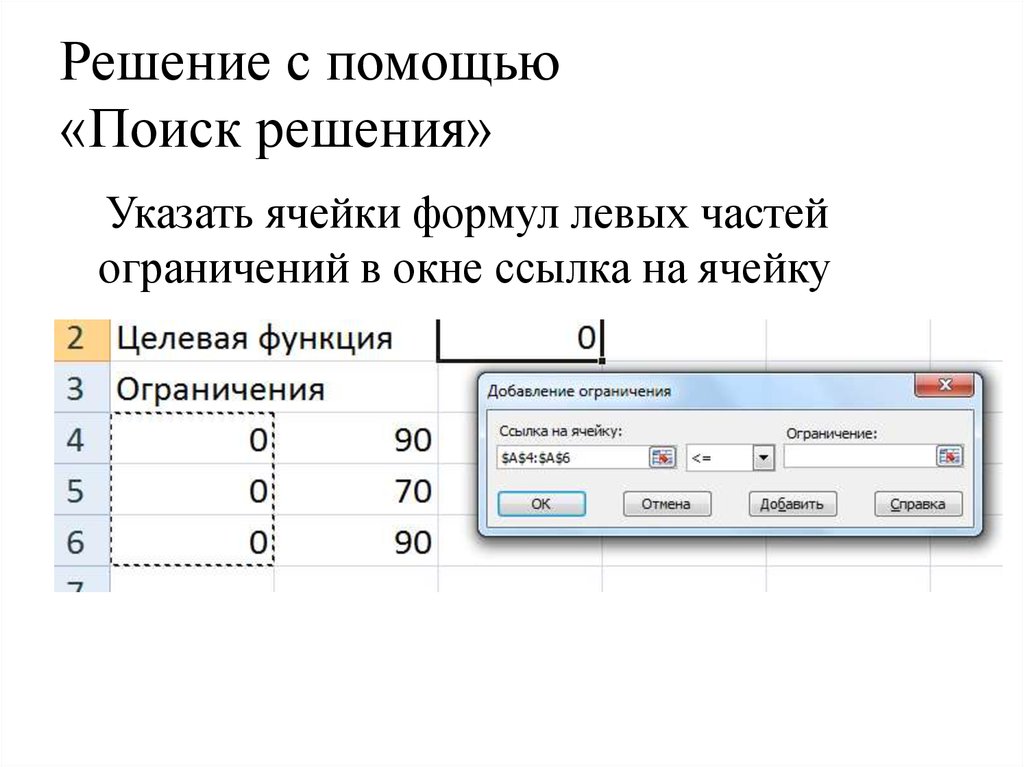
Указать ячейки формул левых частей
ограничений в окне ссылка на ячейку

34. Решение с помощью «Поиск решения»

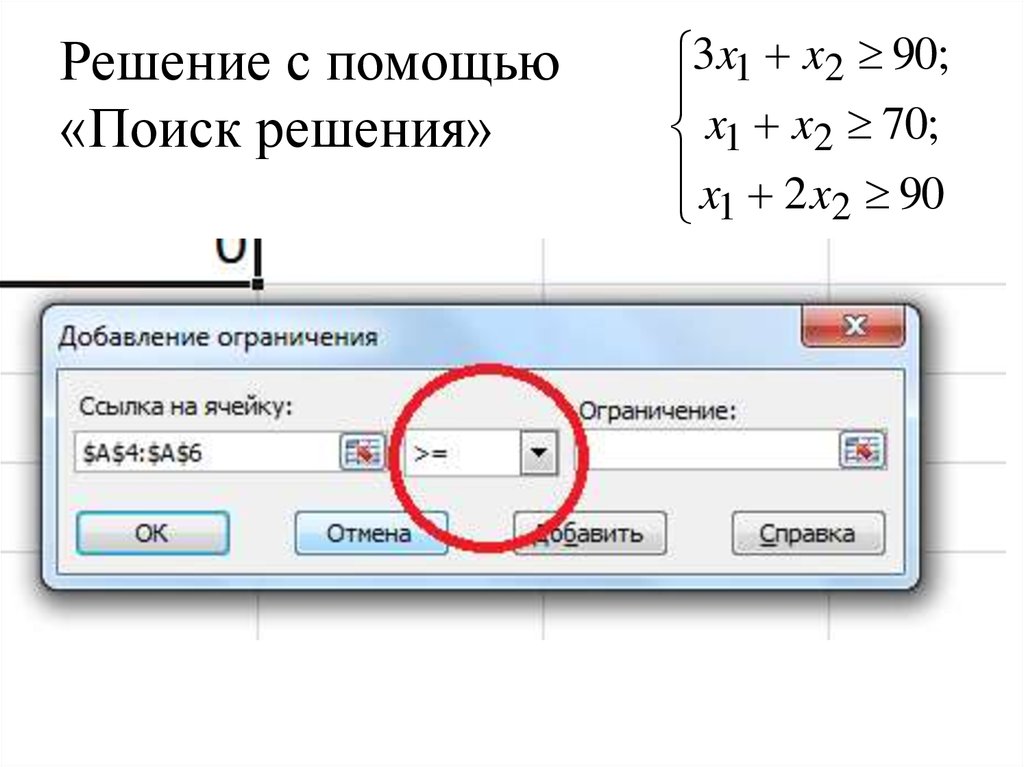
Установить знак неравенства

35. Решение с помощью «Поиск решения»

3x1 x2 90;
x1 x2 70;
x 2 x 90
2
1

36. Решение с помощью «Поиск решения»

Указать ячейки правых частей ограничений в
окне Ограничение - ОК

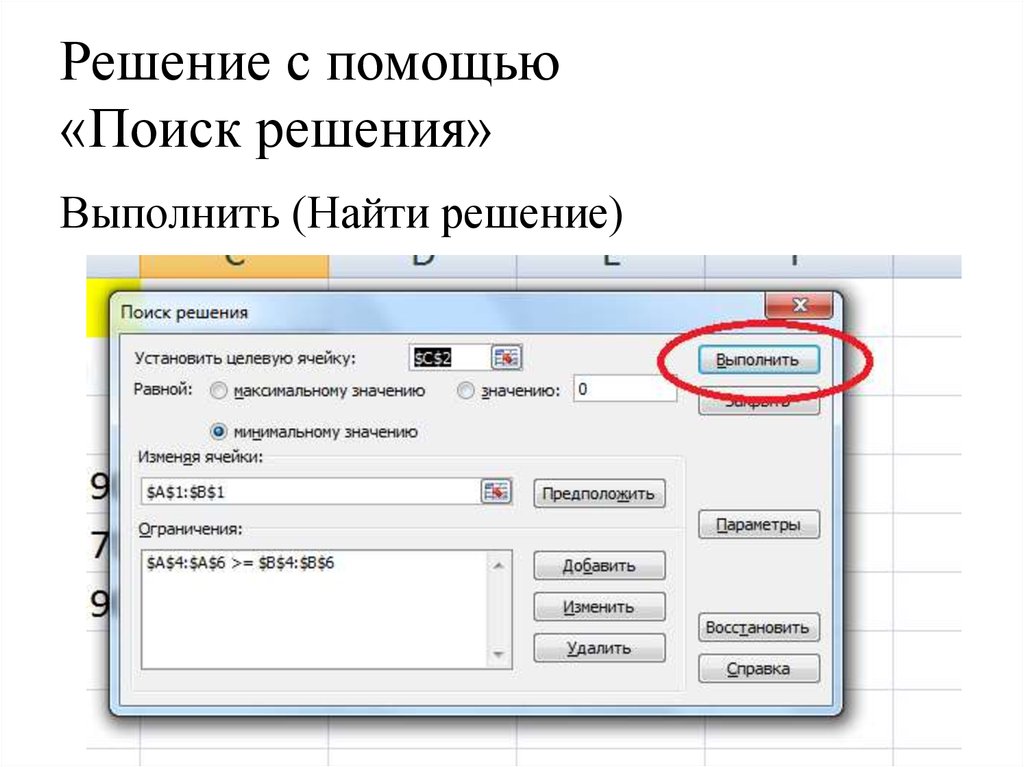
37. Решение с помощью «Поиск решения»

Выполнить (Найти решение)

38. Решение с помощью «Поиск решения»

Сохранить найденное решение – ОК

39. Решение с помощью «Поиск решения»

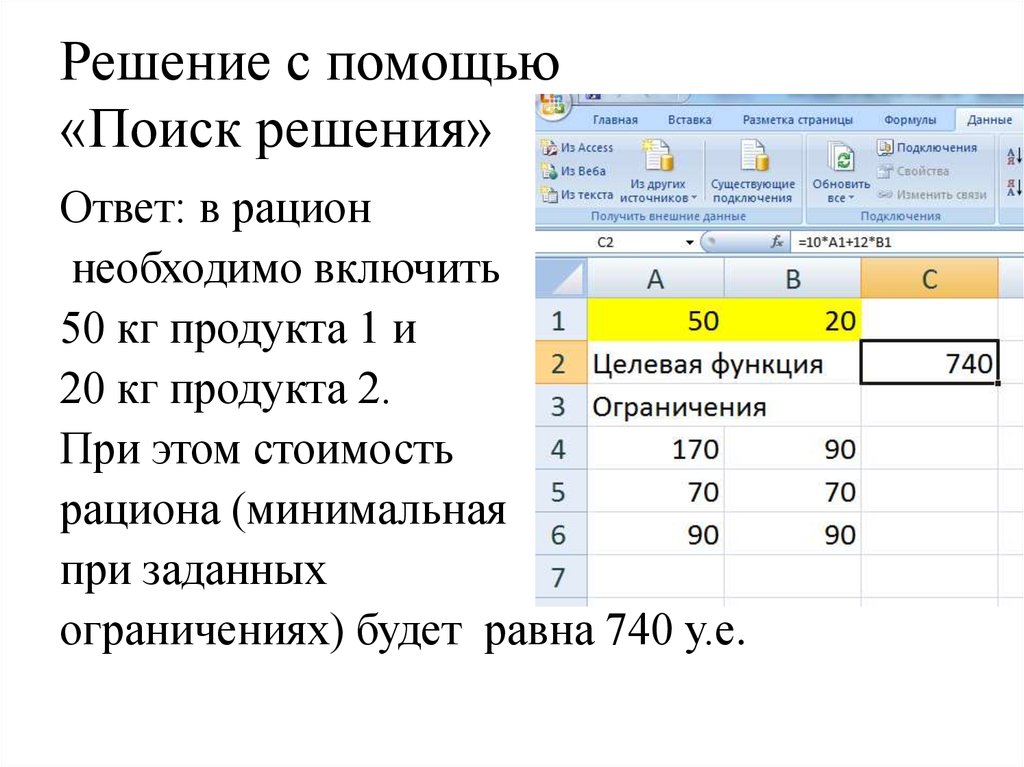
Ответ: в рацион
необходимо включить
50 кг продукта 1 и
20 кг продукта 2.
При этом стоимость
рациона (минимальная
при заданных
ограничениях) будет равна 740 у.е.