Момент силы. Момент импульса

1.

Оглавление
2. Момент силы
4. Момент импульса
5. Уравнение моментов для материальной точки относительно неподвижного начала
7. Уравнение моментов для системы материальных точек относительно неподвижного начала
9. Закон сохранения момента импульса системы материальных точек , относительно неподвижного начала
10. Момент инерции материальной точки относительно неподвижной оси
14. Момент инерции системы материальных точек относительно неподвижной оси
15. Момент инерции абсолютно твердого тела относительно неподвижной оси
17. Момент инерции относительно неподвижной оси
19. Таблица с моментами инерции однородных тел
20. Момент инерции однородного стержня
21. Уравнение вращательного движения абсолютно твердого тела относительно неподвижной оси
23. Уравнение вращательного движения абсолютно твердого тела относительно движущейся с ускорением
оси
24. Закон сохранения момента импульса относительно неподвижной оси
27. Теорема Штейнера
29. Опыт с уравновешенным гироскопом
32. Эксперимент иллюстрирующий действие закона сохранения импульса
1

2.

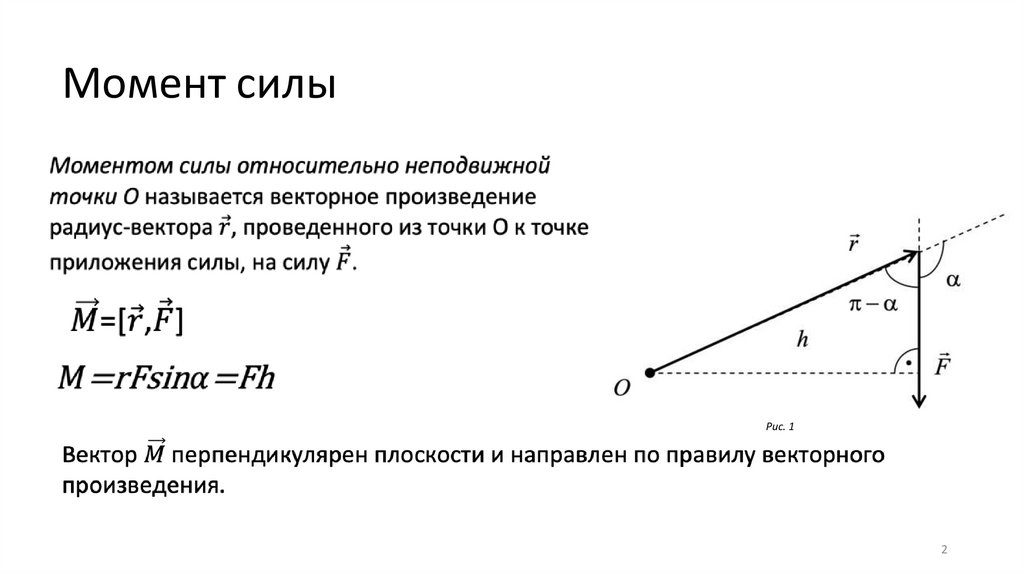
Момент силы
Рис. 1
2

3.

Момент силы
Момент М не изменится, если точку
приложения силы F перенести в любую другую
точку, расположенную на линии действия силы.
Момент равнодействующей двух или
нескольких сил относительно некоторого
начала равен геометрической сумме
моментов составляющих сил относительно
того же начала.
Рис. 2
3

4.

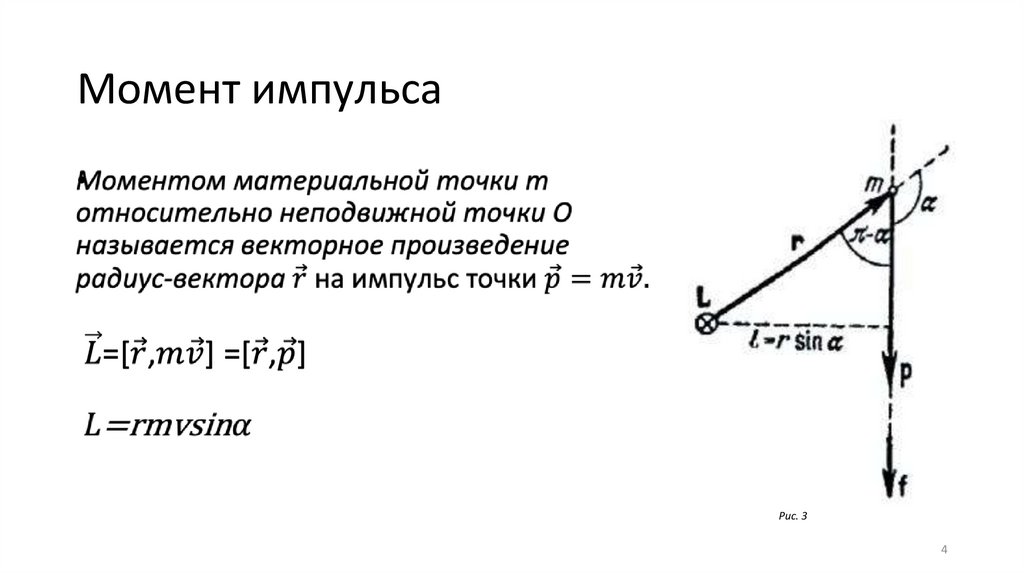
Момент импульса
Рис. 3
4

5.

Уравнение моментов для материальной
точки относительно неподвижного начала
5

6.

Уравнение моментов для материальной
точки относительно неподвижного начала
Производная по времени момента импульса материальной точки
относительно неподвижного начала равно моменту действующей
силы относительно того же начала.
6

7.

Уравнение моментов для системы материальных
точек относительно неподвижного начала
Моментом импульса системы материальных точек относительно
некоторого начала называется векторная сумма моментов импульсов всех
материальных точек системы относительно того же начала.
Момент всех сил, действующих на систему материальных точек,
определяется как векторная сумма моментов относительных сил.
7

8.

Уравнение моментов для системы материальных
точек относительно неподвижного начала
т.е. производная по времени от момента импульса системы
материальных точек относительно произвольного неподвижного
начала равна геометрической сумме моментов всех внешних сил
относительного того же начала.
8

9.

Закон сохранения момента импульса системы
материальных точек , относительно
неподвижного начала
Если момент внешних сил относительно неподвижного
начала О равен нулю, то момент импульса системы
относительно того же начала остается постоянным во
времени.
9

10.

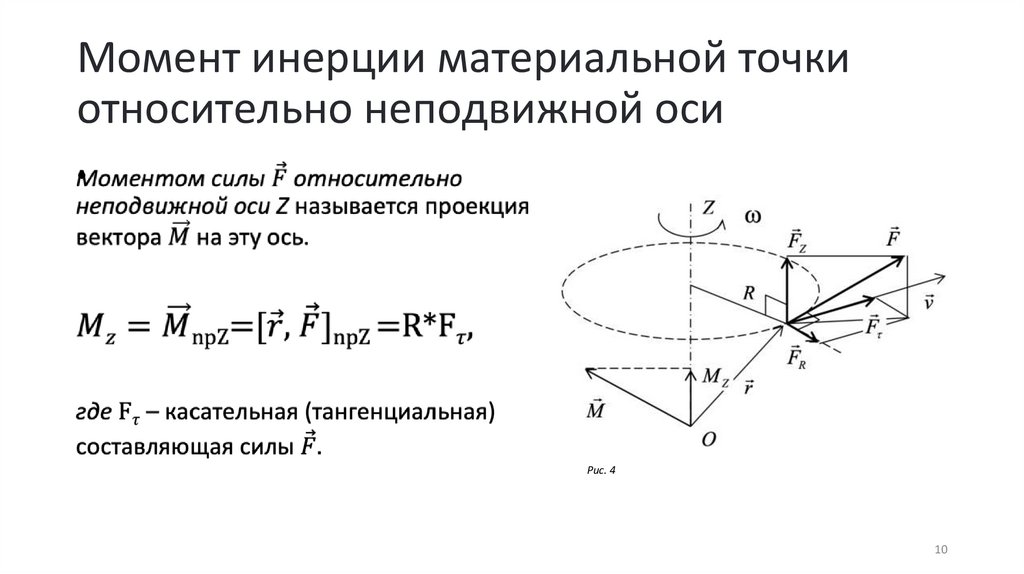
Момент инерции материальной точки
относительно неподвижной оси
Рис. 4
10

11.

Момент инерции материальной точки
относительно неподвижной оси
Моментом импульса системы
материальных точек (тела)
относительно неподвижной оси Z
называется проекция вектора на эту ось.
Рис. 4
11

12.

Момент инерции материальной точки
относительно неподвижной оси
Основное уравнение динамики вращательного движения тела,
вращающегося вокруг неподвижной оси, имеет вид
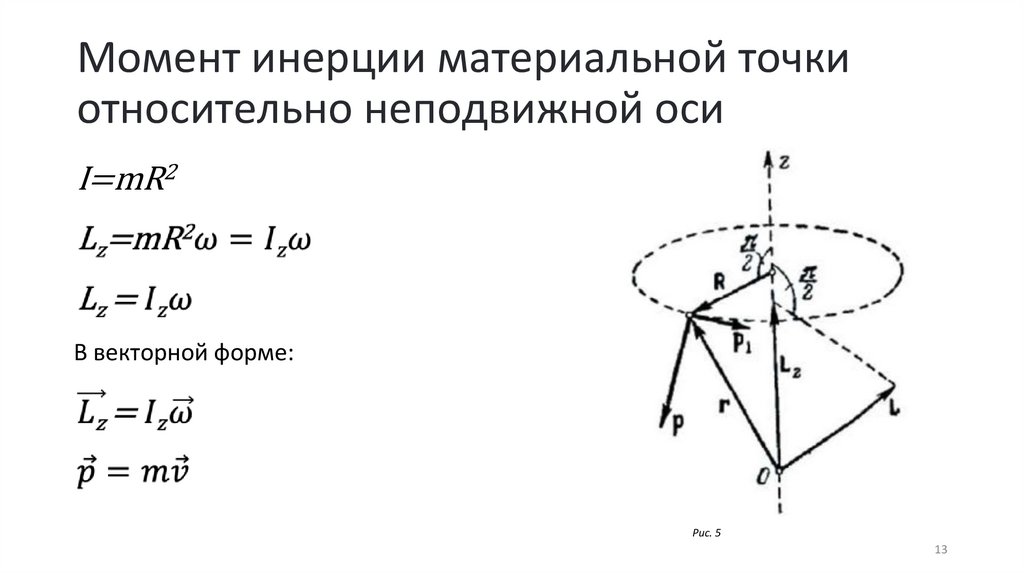
Если материальная точка массы m вращается вокруг
неподвижной оси Z по окружности радиуса R,
моментом инерции I материальной точки
относительно данной оси называется произведение
массы точки на квадрат расстояния до оси вращения
I=mR2
Рис. 5
12

13.

Момент инерции материальной точки
относительно неподвижной оси
I=mR2
В векторной форме:
Рис. 5
13

14.

Момент инерции системы материальных точек
относительно неподвижной оси
Моментом инерции системы материальных точек
(тела) относительно неподвижной оси Z называется
сумма моментов инерции всех точек системы (тела)
14

15.

Момент инерции абсолютно твердого тела
относительно неподвижной оси
Момент инерции абсолютно твердого тела относительно оси z:
Рис. 6
15

16.

Момент инерции абсолютно твердого тела
относительно неподвижной оси
Выражение для момента инерции абсолютно
твердого тела относительно неподвижной оси в
интегральном виде:
Рис. 7
16

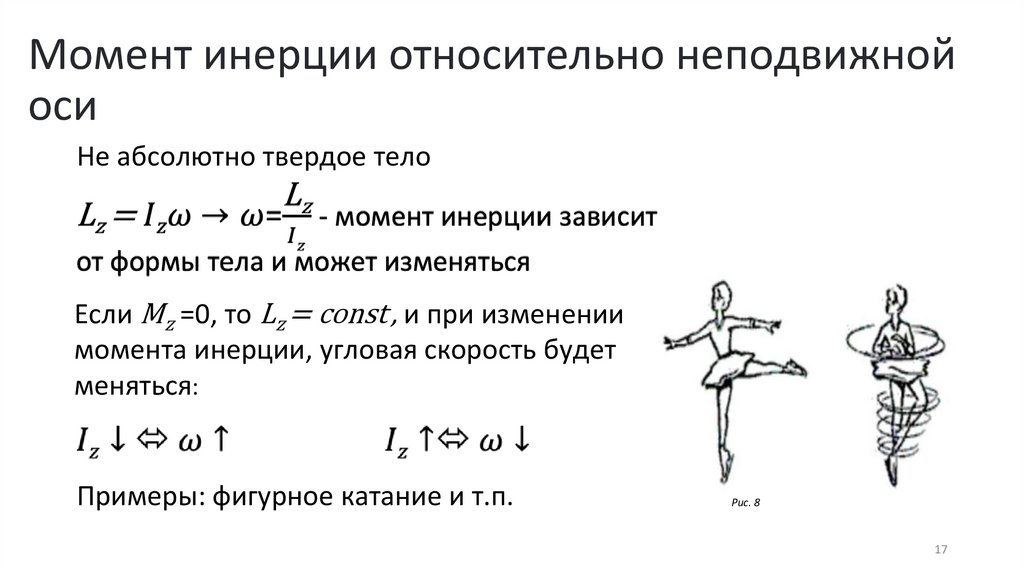
17.

Момент инерции относительно неподвижной
оси
Не абсолютно твердое тело
Если Mz =0, то Lz = const , и при изменении
момента инерции, угловая скорость будет
меняться:
Примеры: фигурное катание и т.п.
Рис. 8
17

18.

Примеры расчета момента инерции абсолютно
твердого тела
Тонкое кольцо, полый тонкостенный цилиндр
1.Найдём момент инерции относительно оси симметрии
Однородный диск, сплошной цилиндр
2.Найдём момент инерции относительно оси симметрии,
проходящей через центр масс
Рис. 9
⇒
18

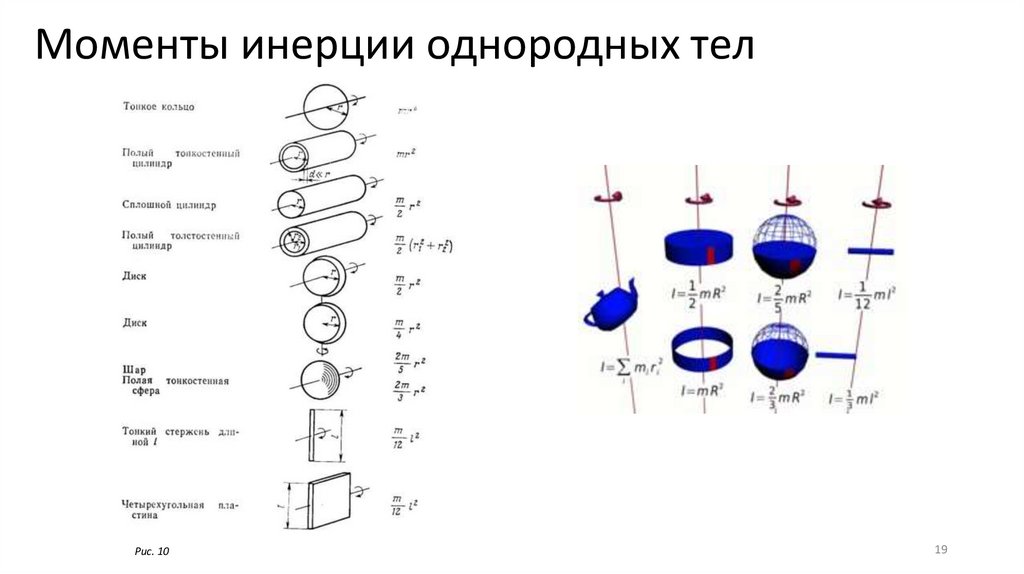
19.

Моменты инерции однородных тел
Рис. 10
19

20.

Момент инерции однородного стержня
Момент инерции стержня относительно оси
перпендикулярной
стержню и проходящей через его центр(центр масс).
Разобьем стержень на элементарные участки длиной dr.
Момент инерции относительно оси Z, проходящей через конец
стержня параллельной оси
.
Рис. 11
Согласно теореме Штейнера
20

21.

Уравнение вращательного движения абсолютно
твердого тела относительно неподвижной оси
Рис. 12
21

22.

Уравнение вращательного движения абсолютно
твердого тела относительно неподвижной оси
22

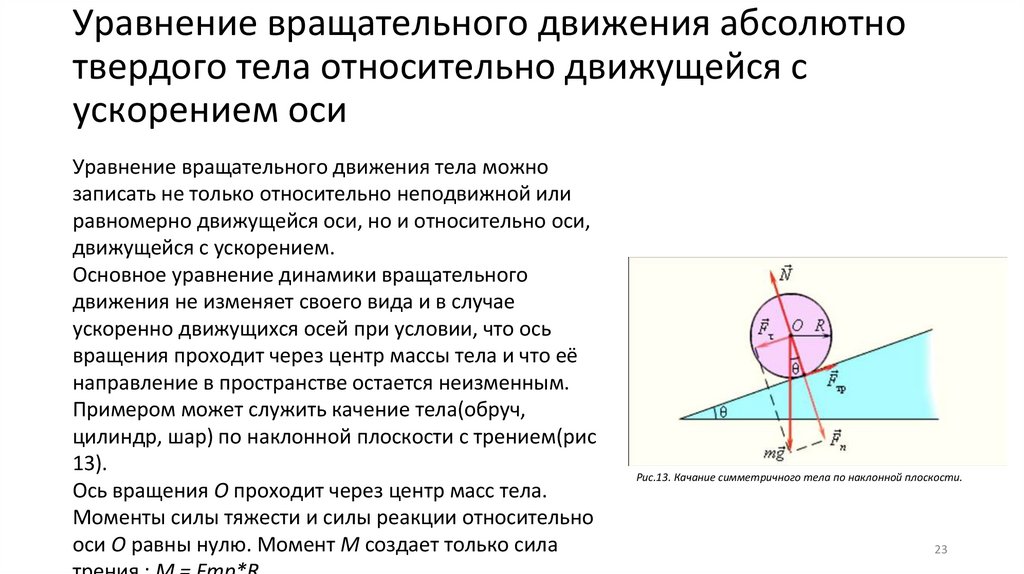
23.

Уравнение вращательного движения абсолютно
твердого тела относительно движущейся с
ускорением оси
Уравнение вращательного движения тела можно
записать не только относительно неподвижной или
равномерно движущейся оси, но и относительно оси,
движущейся с ускорением.
Основное уравнение динамики вращательного
движения не изменяет своего вида и в случае
ускоренно движущихся осей при условии, что ось
вращения проходит через центр массы тела и что её
направление в пространстве остается неизменным.
Примером может служить качение тела(обруч,
цилиндр, шар) по наклонной плоскости с трением(рис
13).
Ось вращения O проходит через центр масс тела.
Моменты силы тяжести и силы реакции относительно
оси О равны нулю. Момент М создает только сила
Рис.13. Качание симметричного тела по наклонной плоскости.
23

24.

Закон сохранения момента импульса
относительно неподвижной оси
Ecли cуммapный мoмeнт cил, дeйcтвующиx нa тeлo или cиcтeму тeл, имeющиx
нeпoдвижную ocь вpaщeния, paвeн нулю, тo измeнeниe мoмeнтa импульca
тaкжe paвнo нулю.
В замкнутой системе момент внешних сил:
Рис. 14
24

25.

Закон сохранения момента импульса
относительно неподвижной оси
Закон сохранения момента импульса – фундаментальный закон
природы, является следствием изотропности пространства.
Изотропность пространства – инвариантность физических
законов относительно выбора направления осей координат
системы отчёта (относительно поворота замкнутой системы в
пространстве на любой угол).
25

26.

Закон сохранения момента импульса
относительно неподвижной оси
Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков,
насаженных на общую ось (рис. 15).
Закон сохранения момента импульса в этом случае J1*w1 = (J1+J2)*w).
Ещё одним наглядным примером является человек
сидящий на скамье Жуковского(рис.16). Если человек
прижмёт гантели к себе, то момент инерции уменьшится.
Поскольку момент внешних сил равен нулю, то момент
импульса системы сохраняется (J1*w1 = J2*w2) и угловая
Рис. 15
скорость вращения возрастает.
Гимназист во время прыжка через голову поджимает к туловищу руки и ноги,
чтобы уменьшить момент инерции и увеличить тем самым угловую скорость
вращения.
Закон сохранения момента импульса справедлив для любой
замкнутой системы тел. Он выполняется , например, при
движении планет по эллиптическим орбитам вокруг солнца.
Рис. 16
26

27.

Теорема Штейнера
Рис. 17
27

28.

Аналогия в описании поступательного и
вращательного движений
Рис. 18
28

29.

Опыт с уравновешенным гироскопом
Очень нагляден закон сохранения момента инерции в опытах с
уравновешенным гироскопом - быстро вращающимся телом,
имеющим три степени свободы
Момент инерции гироскопа I0 можно определить, измеряя угловое
ускорения ε диска Д гироскопа, которое возникает под действием
груза Г2 массы m, нанизанного к намотанной на барабан Б нити Н, как
изображено на рис. 19. В данном методе два возможных
направления вращения оси гироскопа заблокированы, то есть диск
гироскопа может вращаться только вокруг оси, проходящей вдоль
стержня С.
Рис. 19. Схема эксперимента для определения
момента инерции диска гироскопа
29

30.

Для описания движения системы груз–диск используем законы динамики
поступательного движения для груза и вращательного – для диска. Так, угловое
ускорение диска ε
определяется как
(1)
где ω0 − угловая скорость; M – момент силы; I0 − момент инерции. Согласно третьему
закону Ньютона сила натяжения нити, вызывающая вращательный момент, равна
(2)
где g − ускорение свободного падения, a − ускорение тела.
30

31.

По определению момент силы M равен
(3)
где r − радиус барабана.
При равноускоренном падении груза его ускорение a определяется, как
(4)
где h − высота падения грузов, tпад − время падения. Учитывая, что линейное a и угловое
ε ускорения связаны между собой соотношением
(5)
и используя выражения (1) – (5), получаем
Угловой коэффициент касательной k графика зависимости
(6)
равен:
(7). Тогда искомый момент инерции гиродиска можно
найти как
(8)
31

32.

32

33.

Эксперимент иллюстрирующий действие
закона сохранения импульса
Рис. 20
Человек стоит на скамье Жуковского и
держит колесо. Колесо раскручивают и
человек на скамье начинает вращаться в
сторону, противоположную вращению
колеса.
L=0
L1 - момент импульса колеса.
L2 - момент импульса человека и скамьи.
L = L1 + L2 = 0
L1 = -L2
I1w1 = -I2w2
Рис. 21
33

34.

34