Similar presentations:
Момент пары сил
1.
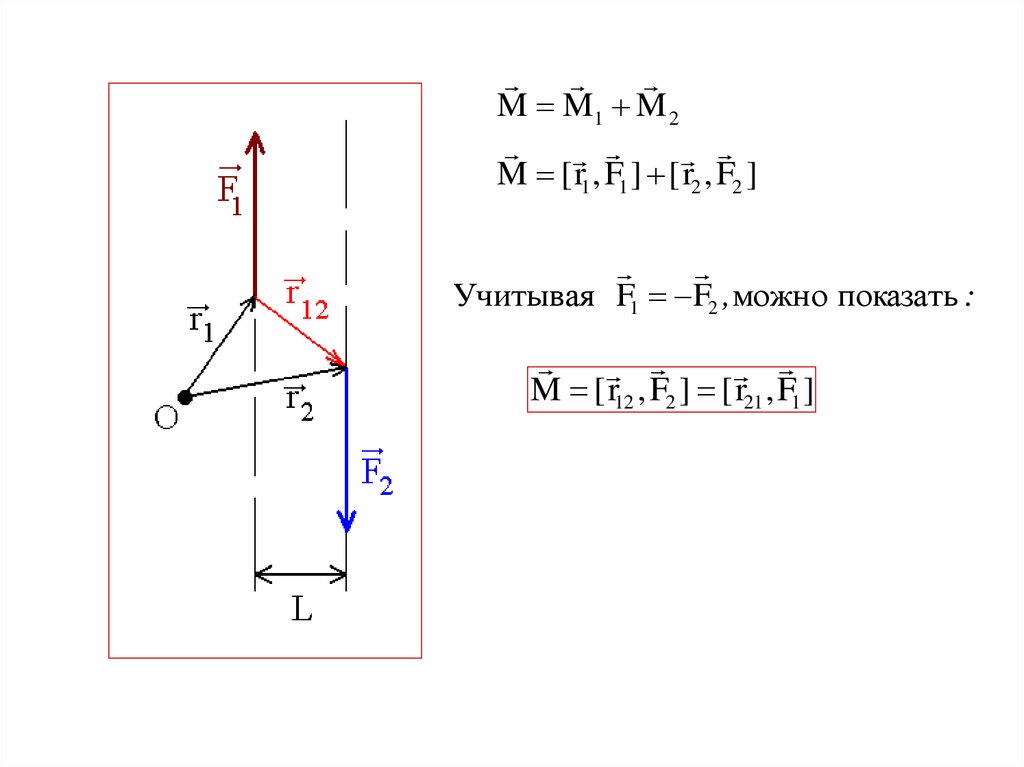
МОМЕНТ ПАРЫ СИЛПара сил - это две равные по модулю и противоположно
направленные силы, не действующие вдоль одной прямой.
Расстояние между прямыми вдоль которых действуют силы
- плечо пары (L).
Определим момент пары сил относительно произвольной
точки О.
2.
M M1 M 2M [ r1 , F1 ] [ r2 , F2 ]
Учитывая F1 F2 ,можно показать :
M [ r12 , F2 ] [ r21 , F1 ]
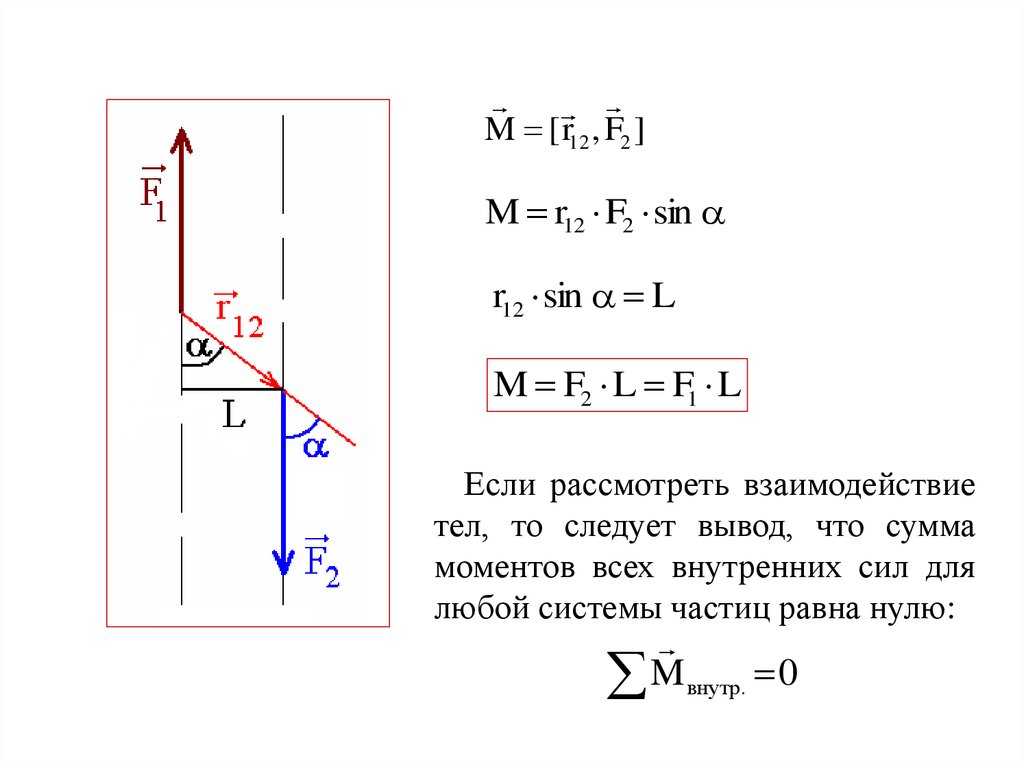
3.
M [ r12 , F2 ]M r12 F2 sin
r12 sin L
M F2 L F1 L
Если рассмотреть взаимодействие
тел, то следует вывод, что сумма
моментов всех внутренних сил для
любой системы частиц равна нулю:
M внутр. 0
4.
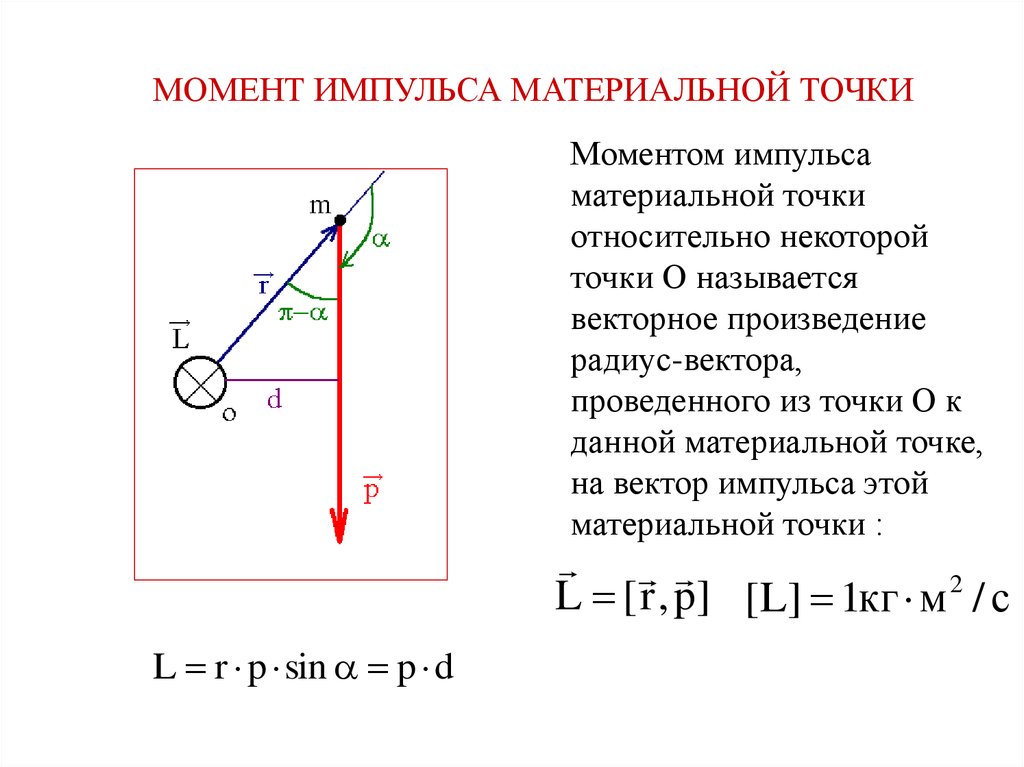
МОМЕНТ ИМПУЛЬСА МАТЕРИАЛЬНОЙ ТОЧКИМоментом импульса
материальной точки
относительно некоторой
точки О называется
векторное произведение
радиус-вектора,
проведенного из точки О к
данной материальной точке,
на вектор импульса этой
материальной точки :
L [ r , p] [L] 1кг м 2 / с
L r p sin p d
5.
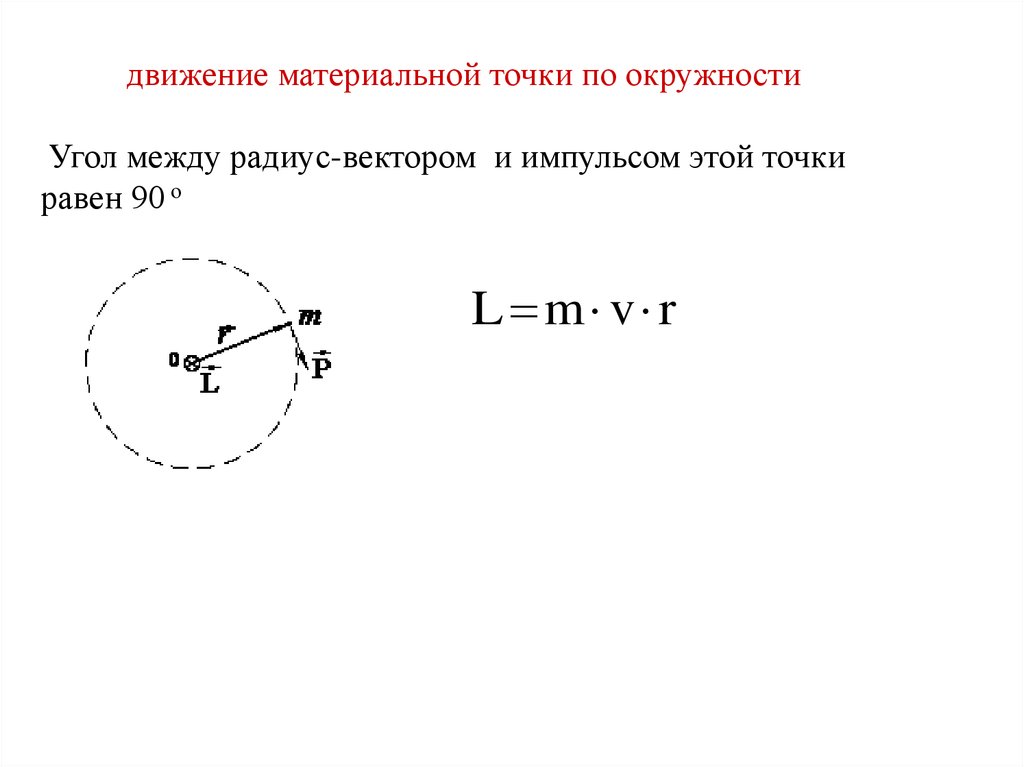
движение материальной точки по окружностиУгол между радиус-вектором и импульсом этой точки
равен 90 о
L m v r
6.
Момент импульса материальной точки относительно некоторойоси Z
Моментом импульса материальной точки относительно
произвольной оси Z называется проекция вектора момента
импульса этой материальной точки относительно любой точки
О, выбранной на оси Z, на данную ось
L z r, p z
7.
Выясним, чем определяется изменение моментаимпульса со временем:
dL d r
dp
[ , p] [ r , ] [ , p] [ r , F]
L [ r , p]
dt
dt
dt
[ , p] p sin 0 0
[ , p] 0
[ r , F] M
На ось Z:
dL z
Mz
dt
dL
M
dt
Полученные равенства можно назвать законом изменения
момента импульса материальной точки.
8.
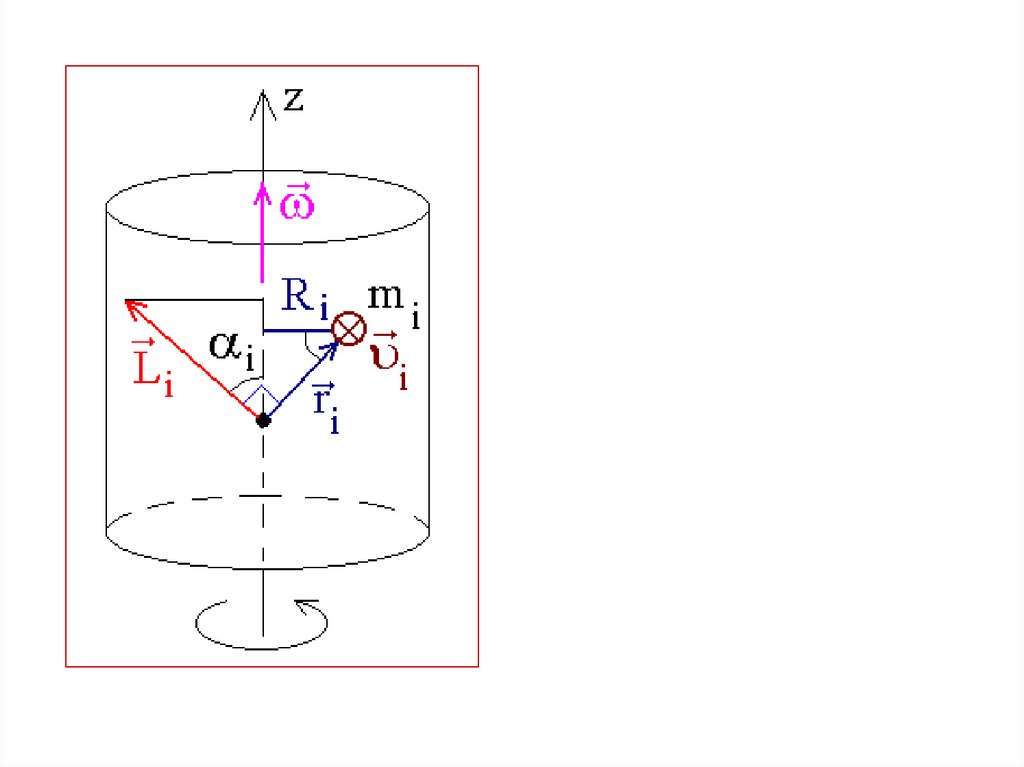
МОМЕНТ ИМПУЛЬСА ТВЕРДОГО ТЕЛАОТНОСИТЕЛЬНО НЕПОДВИЖНОЙ ОСИ ВРАЩЕНИЯ
Момент импульса твердого тела равен сумме моментов
импульсов всех материальных точек, из которых состоит тело.
Выберем на оси Z произвольную точку О. Разобьем тело
на материальные точки.
Момент импульса материальной точки относительно точки О
равен
L i ri , Pi Δ m i ri , v i
9.
10.
Тогда момент импульса всего тела относительно точки О :n
n
L L i Δ m i ri , v i
i 1
i 1
Найдем момент импульса тела относительно оси вращения Z.
Lzi Li cos i Δ mi vi ri cos i Δ mi vi R i
Учтем взаимосвязь :
vi ω R i
Тогда
L zi ω Δ m i R
2
i
11.
Момент импульса тела относительно оси равен суммемоментов импульсов всех точек этого тела
относительно этой оси:
n
n
L z L zi ω Δ m i R
i 1
i 1
2
i
Таким образом, момент импульса тела относительно оси не
зависит от выбора положения точки О.
12.
ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСАРассмотрим механическую систему, состоящую из n тел
(материальных точек).
M ij моменты внутренних сил
M i - суммарный момент внешних
сил, действующих на i-е тело
13.
dL1dt M12 M13 ... M1n M1
dL 2 M
21 M 23 ... M 2 n M 2
dt
dL n
dt M n1 M n 2 ... M n ,n 1 M n
14.
d(L1 L 2 ... L n )M1 M 2 ... M n
dt
Сумма моментов внутренних сил системы тел
равна нулю (рассмотрено ранее).
L L1 L 2 ... L n - полный момент импульса системы тел
Mвнешн. M1 M 2 ... M n - сумма моментов внешних сил,
действующих на тела системы
15.
dLM внешн.
dt
dL z
M внешн.,z
dt
На ось
Z:
M внешн. 0
Если система замкнута, то: dL
dt 0 L const
Закон сохранения момента импульса: Момент импульса
замкнутой системы тел остается постоянным.
Если вращение взаимодействующих тел относительно некоторой
неподвижной оси Z. В этом случае может сохраняться суммарный
момент импульса системы относительно данной оси Lz.
В частном случае : если Мвнешн. (z) = 0, то Lz = const.
16.
МОМЕНТ ИНЕРЦИИМомент инерции - скалярная физическая величина,
характеризующая инертные свойства тел при вращательном
движении.
Момент инерции материальной точки относительно оси:
I m r2
[I] = 1 кг м2
17.
Представим произвольное тело как совокупность частиц(материальных точек). Тогда момент инерции этого тела
относительно заданной оси вращения равен:
n
I m j rj2
m j j Vj
j 1
n
I j r Vj
j 1
2
j
I r 2 dm r 2 dV
18.
19.
Момент инерции I относительно произвольной оси равенсумме момента инерции I0 относительно оси, параллельной
данной и проходящей через центр масс тела, и произведения
массы тела m на квадрат расстояния а между осями.
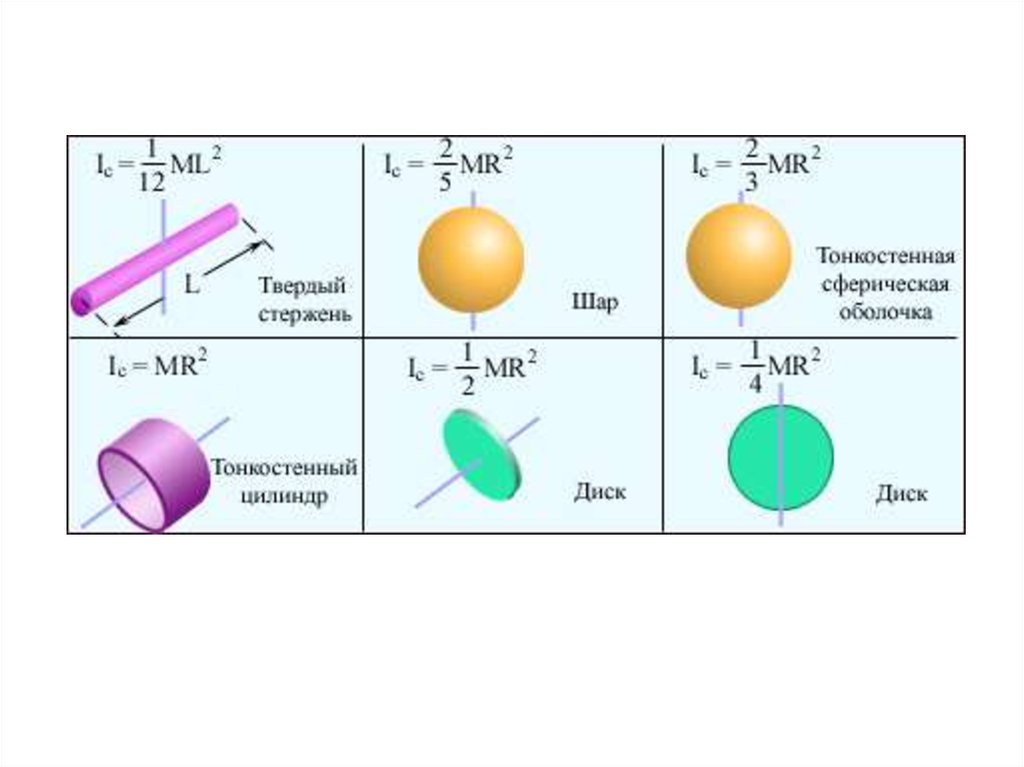
Теорема Штейнера:
I I 0 ma 2
2
I mR 2 ma 2
5
20.
ОСНОВНОЙ ЗАКОНДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Скорость изменения момента импульса материальной точки
равна моменту сил, действующих на эту точку. Подобное
утверждение справедливо и для момента импульса
материальной точки относительно некоторой оси Z:
dL
M
dt
и
Данные равенства можно назвать
момента импульса материальной точки.
dL z
Mz
dt
законом
изменения
21.
Запишем последнее равенство для каждой точкивращающегося тела, а затем просуммируем по всем
точкам тела:
dL zi
M zi
dt
n
d n
L zi M zi
dt i 1
i 1
n
dL z n
M zi внутр. M zi внеш.
dt
i 1
i 1
В последнем равенстве
относительно оси Z,
n
M
i 1
zi внутр.
0
Тогда для всего тела
Lz – момент импульса тела
n
M
i 1
zi внеш.
dL z
M z внеш.
dt
М z _ внеш .
22.
Было получено, чтоn
n
L z L zi ω Δ m i R i2
i 1
Тогда
i 1
Lz I ω
Учитывая, что момент инерции абсолютно твердого тела –
постоянная величина, получим:
d
I ω M z внеш.
dt
dω
обозначим
εz
dt
dω
I
M z внеш.
dt
εz – проекция вектора углового
ускорения на ось Z
23.
Тогда окончательно получаем:I ε z M z внеш.
Основной закон динамики вращательного движения
твердого тела относительно неподвижной оси. Его можно
записать и для модулей входящих в него величин:
M внеш.
ε
I
Закон динамики вращательного движения:
Модуль
углового ускорения тела прямо пропорционален модулю
суммарного момента внешних сил, приложенных к телу и
обратно пропорционален моменту инерции тела.







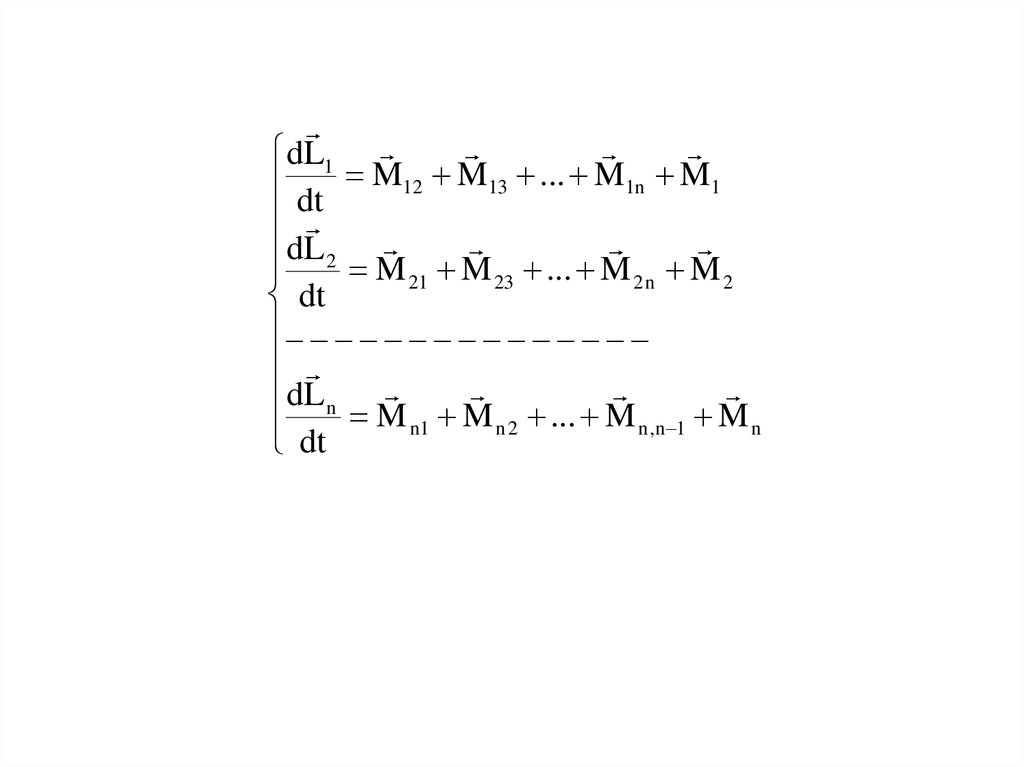









 physics
physics








