Лекція 3. Тема 1.3. Метричні і позиційні властивості прямокутних проекцій пар елементарних геометричних фігур

1. Лекція 3 Тема 1.3. Метричні і позиційні властивості прямокутних проекцій пар елементарних геометричних фігур

План викладу матеріалу
13. Належність прямої і точки площині.
14. Перетин прямої з площиною.
15. Перетин двох площин довільного положення.
16. Паралельність прямої та площини. Паралельність площин
17 Перпендикулярність прямої і площини.
18. Взаємноперпендикулярні площини.
19. Кут між прямою і площиною та між двома площинами.

2.

Позиційними називаються задачі, в яких визначається взаємне
розташування окремих геометричних елементів відносно один
одного.
До таких задач належать задачі на взаємну належність одних
геометричних елементів іншим; на перетин – побудова точки перетину
прямої і площини, двох прямих, лінії перетину двох площин тощо. При
розв’язанні позиційних задач не враховуються їх метричні властивості.
Метричними називаються задачі на вимірювання відрізків,
кутів, визначення дійсної величини плоских фігур тощо.
Розв’язання
багатьох
метричних
задач
вимагає
побудови
перпендикулярних прямих, площин і т.п.
Різновидів метричних задач багато, проте кожна з них складається з
двох основних:
Визначення відстані між двома точками;
Визначення кута між перетинними прямими (кут між геометричними
елементами вимірюється кутом між двома прямими, що перетинаються)

3. 13. Належність прямої і точки площині

Для побудови зображення прямої лінії, яка лежить
у даній площині використовують відомі з елементарної
геометрії твердження:
Пряма лінія належить площині, якщо дві її точки
належать даній площині.
Пряма належить площині у тому випадку, коли
вона проходить через одну з точок даної площини
паралельно будь-якій прямій, яка лежить в цій площині.
Будь-яка пряма належить площині, заданої
трикутником, так як вона має з нею цілий ряд спільних
точок.
B2
12
Приклад
Площина задана паралельними прямими АВ і СD.
Необхідно побудувати фронтальну проекцію прямої, яка
лежить в цій площині, якщо задано її горизонтальну
проекцію.
Визначимо за допомогою ліній зв’язку фронтальні
проекції точок 1 і 2 (12, 22), що лежать у площині заданої
паралельними прямими. Через точки 12 і 22 побудуємо
фронтальну проекцію прямої.
D2
22
A2
C2
A1
C1
21
11
B1
D1

4. Пряма, що лежить у площині заданої слідами, повинна мати сліди які б лежали на однойменних слідах цієї площини, чи мати з одним

зі слідів спільну точку та бути паралельною іншому.
N2
X12
К1 К2
M2
f2
f2
h2 f 1
X12
N1
m2
К1 К2
m1
M1
h1
h1

5. Твердження Точка належить площині, якщо вона належить прямій, яка належить даній площині.

Твердження
Точка належить площині,
належить даній площині.
якщо
вона належить
прямій,
яка
Приклад
У площині, заданої трикутником АВС, побудувати точку D.
Побудуємо в трикутнику АВС будь-яку пряму, наприклад С1 (С111;
С212), і візьмемо на цій прямій точку D(D1; D2). Проекції точки повинні
належати однойменним проекціях прямої С1 (інакше D1ε С111; D2 εС212).
B2
12
D2
A2
C2
B1
11
A1
D1
C1

6. 14. Перетин прямої з площиною

P
Побудова точки перетину прямої з
площиною
є
першою
основною
позиційною задачею, яка зводиться до
визначення
точки,
що
одночасно
належить заданій прямій і площині.
Площина
АВСD
–
фронтальнопроекціювальна.
Отже,
фронтальна
проекція
площини
–
пряма
лінія,
фронтальна проекція точки К співпадає з
фронтальною
проекцією
площини.
У
перетині фронтальної проекції прямої 1222 з
фронтальною проекцією площини знайдемо
фронтальну
проекцію
К2
точки
К.
Горизонтальну проекцію К1 точки К
знайдемо за допомогою лінії зв’язку К1К2.
При цьому необхідно мати на увазі, що
горизонтальна проекція К1 буде лежати на
горизонтальній проекції прямої 1121.
К
D2 C2
12
К2
22
A2 B2
21
C1
B1
К1
A1
D1
11

7.

Для побудови точки перетину прямої з площиною загального
положення необхідно:
Провести через дану пряму L допоміжну площину T (за допоміжні площини
вибирають проекціювальні площини і задача зводиться до визначеня лінії перетину
двох площин одна з яких проекціювальна);
Побудувати лінію перетину допоміжної площини T із заданою АВСD;
Знайти точку перетину К(К1, К2), побудованої прямої 12 із заданою L, яка й буде
шуканою.
Видимість визначаємо за допомогою конкуруючих точок, з яких одна належить
прямій, а друга площині. Це точки 1–3 і точки 4–5.
A2
B2
Fp2
FQ2
L2
42 52
22
К2
12
32
D2
L2
X12
C2
Кp1 Кp2
К2
M2
К1
B1
A1
L1
41
11 31
К1
D1
N2
21
51
C1
T1
M1
L1 G1 GQ1
Gp2 Fp1
N1
Gp1

8. 15. Перетин двох площин довільного положення

При перетині двох площин одна з яких проекціювальна, задача на
побудову лінії перетину двох площин зводиться до попередньої задачі – на
побудову точок перетину прямої з площиною.
D2
E2
12
N2
Q
К2
P
22
A2
К1
C2
B2
M2
B1
D1 N1
11
A1
21
C1
E1 M1

9. Правила

Для побудови лінії перетину двох площин необхідно
побудувати будь-які дві точки, кожна з яких належить обом
площинам. Ці точки і будуть визначати шукану лінію.
Для побудови лінії перетину двох площин загального
положення необхідно, узяти на одній з площин дві будь-які
прямі і побудувати точки перетину їх з іншою площиною. Таким
чином, задача зводиться до розв’язання задачі на перетин
прямої з площиною загального положення.
Якщо площини задані слідами, то точки, які визначають пряму
перетину цих площин, будуть точками перетину однойменних
слідів площин.

10. Перетин площин загального положення

Q2
P2
E2
A2
12
B2
32
К2
M2
N2
N2
42
C2
22
D2
X12
E1
N1
К1
D1
Кр1 Kp2
M2
N1
KQ1 KQ2
C1
31
11
A1
f P2
f Q2
21
B1
41
hQ1
M1
M1
hP1

11. 16. Паралельність прямої та площини. Паралельність площин

Пряма паралельна площині,
якщо вона паралельна будь-якій
прямій, яка лежить в цій
площині.
Таким
чином,
щоб
побудувати пряму яка б була
паралельна площині, необхідно
в
даній площині задатись
прямою і паралельно до неї
провести шукану.
B2
A2
E2
D2
B1
E1
К2
A1
D1
К1

12. Дві площини будуть паралельними, якщо дві перетинаючися прямі однієї площини, відповідно, паралельні двом перетинаючимся прямим

іншої площини
22
32
C2
C2
D2
42
12
A2
B2
E2
B2
A2
31 41
D2
C1 D1
D1
A1
K1
C1
11 21
A1 B1
K2
б
E1
B1
Горизонталі і фронталі паралельних площин паралельні між собою.

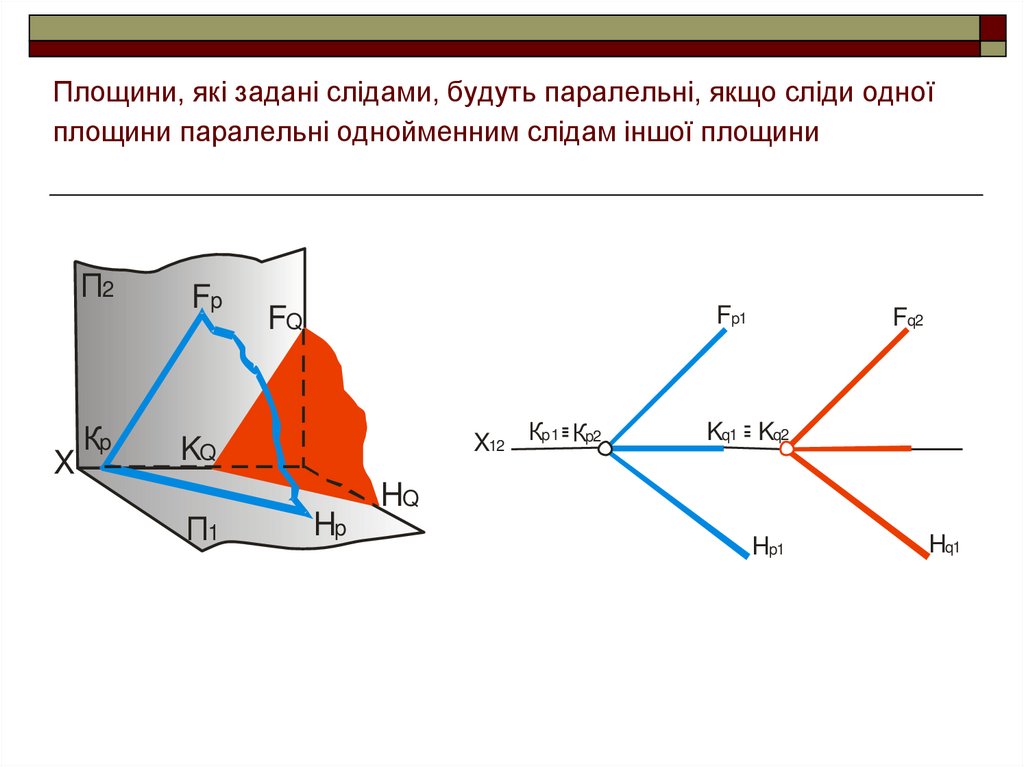
13. Площини, які задані слідами, будуть паралельні, якщо сліди одної площини паралельні однойменним слідам іншої площини

П2
X
Кp
Fp
Fp1
FQ
X12 Кp1 Кp2
KQ
П1
Hp
Fq2
Kq1 Kq2
HQ
Hp1
Hq1

14. 17. Перпендикулярність прямої і площини

З елементарної геометрії відомо, що пряма буде перпендикулярною до площини, якщо
вона перпендикулярна до двох перетинних прямих, які лежать в даній площині.
А
90°
Р
90°
β
Прямий кут між прямою, що лежить в площині і перпендикуляром до неї,
спроекціюється в дійсну величину (90º) тільки у тому випадку, якщо одна з його сторін
паралельна площині проекцій.
Таким чином, щоб побудувати перпендикуляр до площини, необхідно взяти в цій
площині прямі, які б були паралельні площинам проекцій (прямі рівня – горизонталі і
фронталі) і провести перпендикуляри до цих прямих.

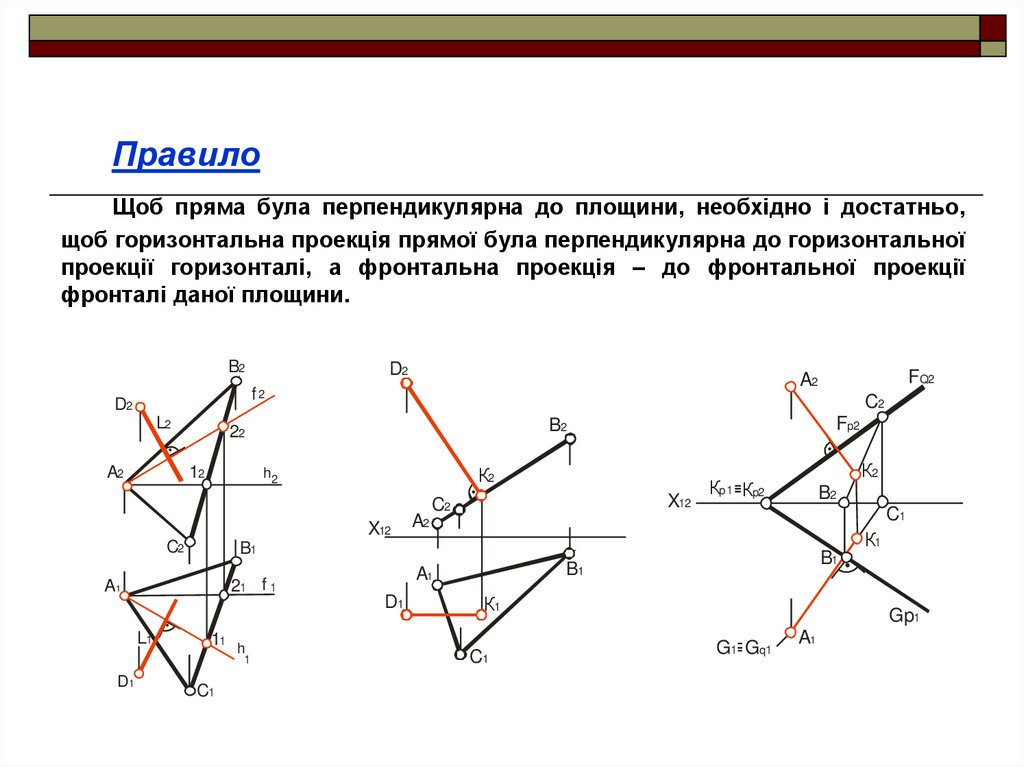
15. Правило

Щоб пряма була перпендикулярна до площини, необхідно і достатньо,
щоб горизонтальна проекція прямої була перпендикулярна до горизонтальної
проекції горизонталі, а фронтальна проекція – до фронтальної проекції
фронталі даної площини.
B2
D2
D2
L2
C2
Fp2
B2
22
12
К2
h2
A2
X12
C2
A2
X12
C2
К2
Кp1 Кp2
B2
C1
B1
B1
A1
D1
B1
К1
Gp1
11 h
1
D1
C1
C1
К1
21 f 1
A1
L1
FQ2
A2
f2
G1 Gq1
A1

16. Алгоритм розв’язування задачі:

побудувати в даній площині Р(∆АВС) прямі рівня – горизонталь
і фронталь;
з горизонтальної проекції точки D1 провести пряму,
перпендикулярну до горизонтальної проекції горизонталі h1 (L1 горизонтальна проекція перпендикуляра);
з фронтальної проекції точки D2 провести пряму
перпендикулярну до фронтальної проекції фронталі f2.
L2 –

17. 18. Взаємноперпендикулярні площини

Правило
Дві площини перпендикулярні, якщо одна з них проходить через
перпендикуляр до другої площини чи перпендикулярна до прямої, яка
належить цій площині.
B2
E2
L2
P
A2
A
f2
22
j
11 2
D2
C2
B1
D1
90°
C
B
Q
A1
21
f1
E1
11
C1
L1
j1

18. 19. Кут між прямою і площиною та між двома площинами

Кут між прямою і площиною вимірюється кутом між прямою та її
проекцією на цю площину.
F2
A2
L2
A
B
F1 H2
X12
P
N1
A1
C
N2
L1
H1

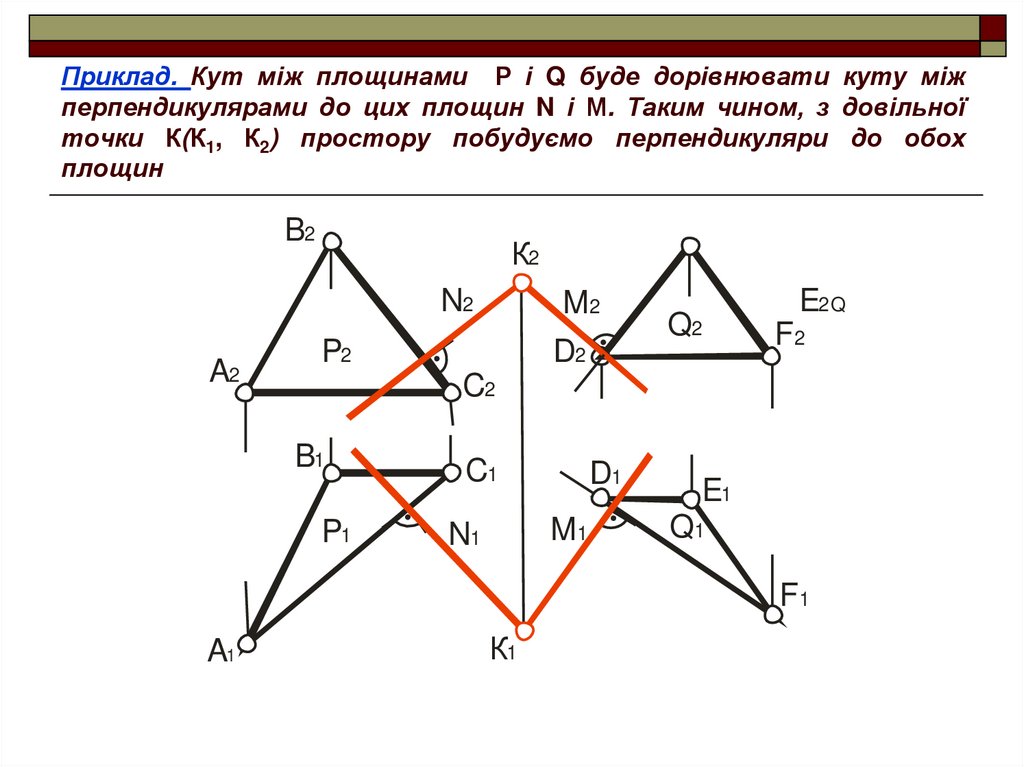
19. Приклад. Кут між площинами Р і Q буде дорівнювати куту між перпендикулярами до цих площин N і М. Таким чином, з довільної точки

К(К1, К2) простору побудуємо перпендикуляри до обох
площин
B2
К2
N2
Q2
D2
A2
P2
M2
E2Q
F2
C2
B1
D1
M1
N1
P1
C1
E1
Q1
F1
A1
К1

20. Запитання і завдання для самоперевірки

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
Як побудувати прямі лінії і точки, що належать площині?
Подати алгоритм і приклади побудови прямих ліній, паралельних до площин.
Показати приклади і алгоритм визначення точки перетину прямої з площиною
загального положення і проекціювальною площиною.
Як установити взаємне положення прямої і площини?
Як визначити „видимість” при перетині прямої з площиною?
Які дії і в якій послідовності необхідно їх виконувати при визначенні лінії перетину
двох площин?
У якому випадку дві площини будуть паралельні?
Показати на прикладі побудову двох взаємно паралельних площин.
Показати приклади і алгоритм побудови прямої перпендикулярної до площини.
Як побудувати перпендикуляр з точки на пряму загального положення (за
допомогою площини перпендикулярної до прямої)?
В якому випадку дві площини будуть перпендикулярні одна одній?
Як побудувати дві взаємноперпендикулярні площини?
Встановити чи перпендикулярні площини загального положення одна одній, якщо їх
однойменні сліди взаємноперпендикулярні?
Що називається кутом між прямою і площиною і які дії необхідно виконати для
побудови проекцій цього кута на кресленику?
Які дії необхідно виконати для побудови на кресленику проекцій лінійного кута для
даного двогранного кута?