Similar presentations:
Логические основы компьютера
1.
Михаилиди И.М.ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА
2.
ВЫСКАЗЫВАНИЯВысказывание - это повествовательное
предложение, про которое можно всегда
определенно сказать истинно оно или ложно
Какие из этих предложений являются
высказыванием?
1. Идет дождь
2. Два плюс два равно пяти
3. Сумма углов треугольника равна 1800
4. Сегодня четверг
5. Петр Петрович живет в Москве
6. За февралем следует октябрь
7. Москва – столица России
8. Солнце – ближайшая к Земле звезда
3.
ВЫСКАЗЫВАНИЯЛогические значения – истина, true (1),
ложь, false (0)
Логическое высказывание - утверждение, которому
всегда можно поставить в соответствие одно из
двух логических значений: ложь (0) или истина
(1)
Логическая переменная – абстрактная величина,
которая может принимать логические значения:
истина (1) или ложь (0)
4.
ЛОГИЧЕСКИЕ ОПЕРАЦИИЛогические операции - операции над логическими
значениями и переменными, результатом
которых является одно из двух возможных
логических значений: истина (1) или ложь (0).
Логические операции:
─ конъюнкция
Λ (&)
─ дизъюнкция
V
─ инверсия
¬
─ импликация
→
─ эквивалентность ↔ (=)
Значение логической операции вычисляется по
таблице истинности
5.
ВЫЧИСЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАЦИЙИнверсия:
F = ¬A
истинна тогда и только тогда, когда операнд
ложен и наоборот
A
F = ¬A
1
0
0
1
6.
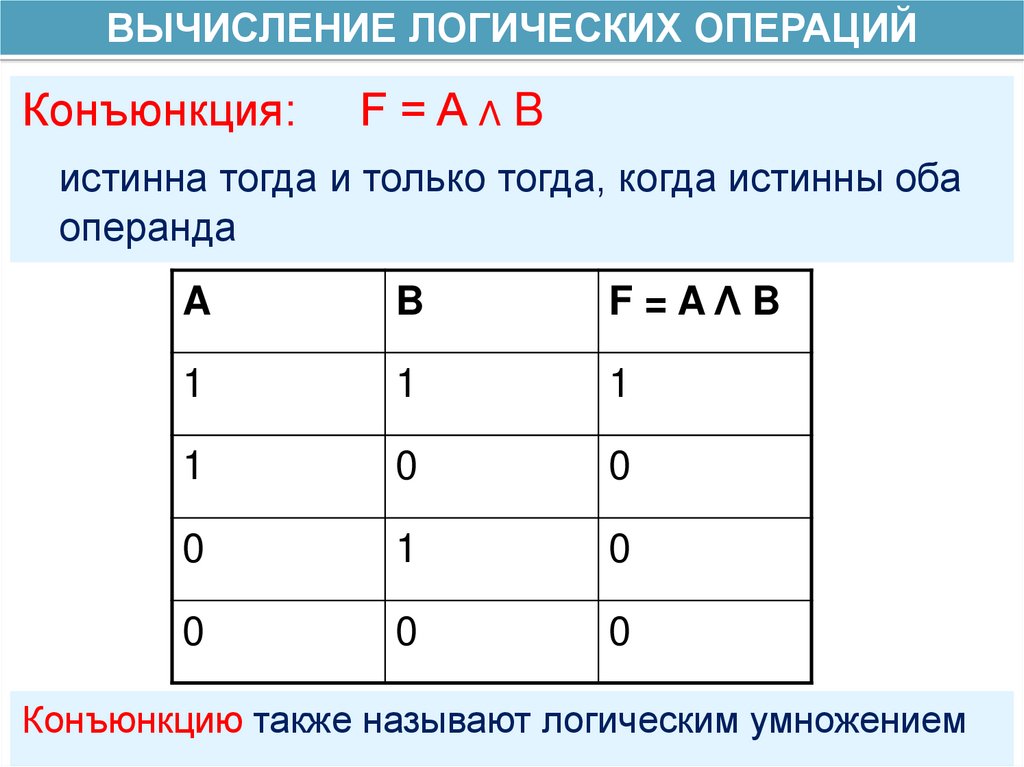
ВЫЧИСЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАЦИЙКонъюнкция:
F=AΛB
истинна тогда и только тогда, когда истинны оба
операнда
A
B
F =AΛ B
1
1
1
1
0
0
0
1
0
0
0
0
Конъюнкцию также называют логическим умножением
7.
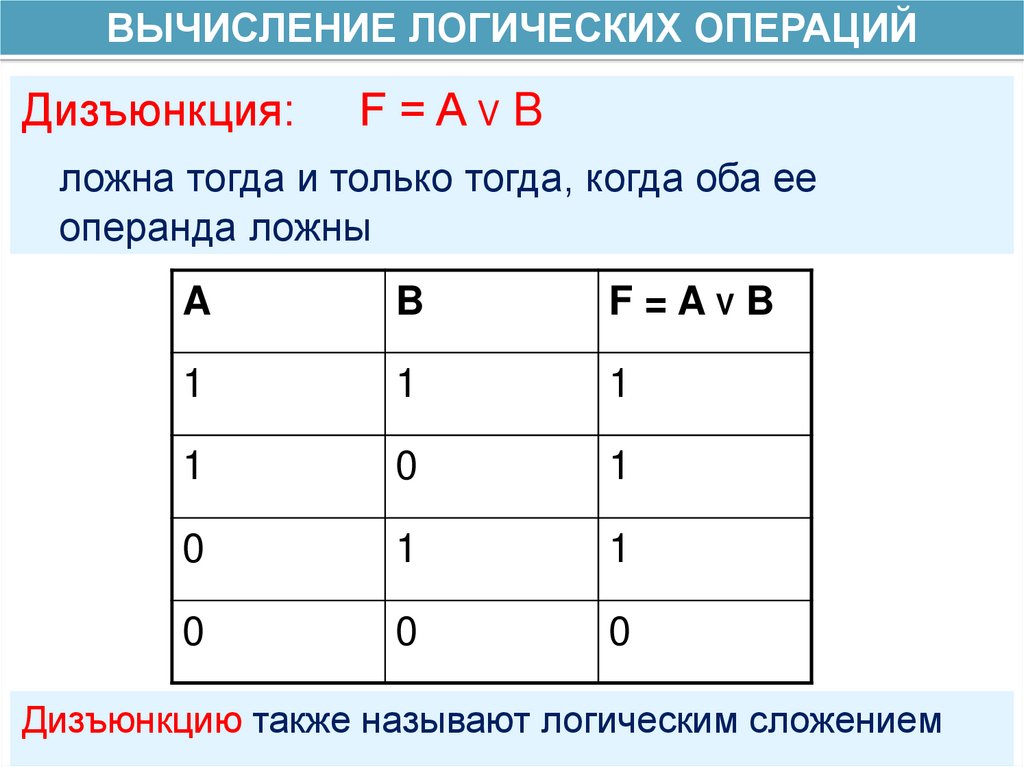
ВЫЧИСЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАЦИЙДизъюнкция:
F=AVB
ложна тогда и только тогда, когда оба ее
операнда ложны
A
B
F=AVB
1
1
1
1
0
1
0
1
1
0
0
0
Дизъюнкцию также называют логическим сложением
8.
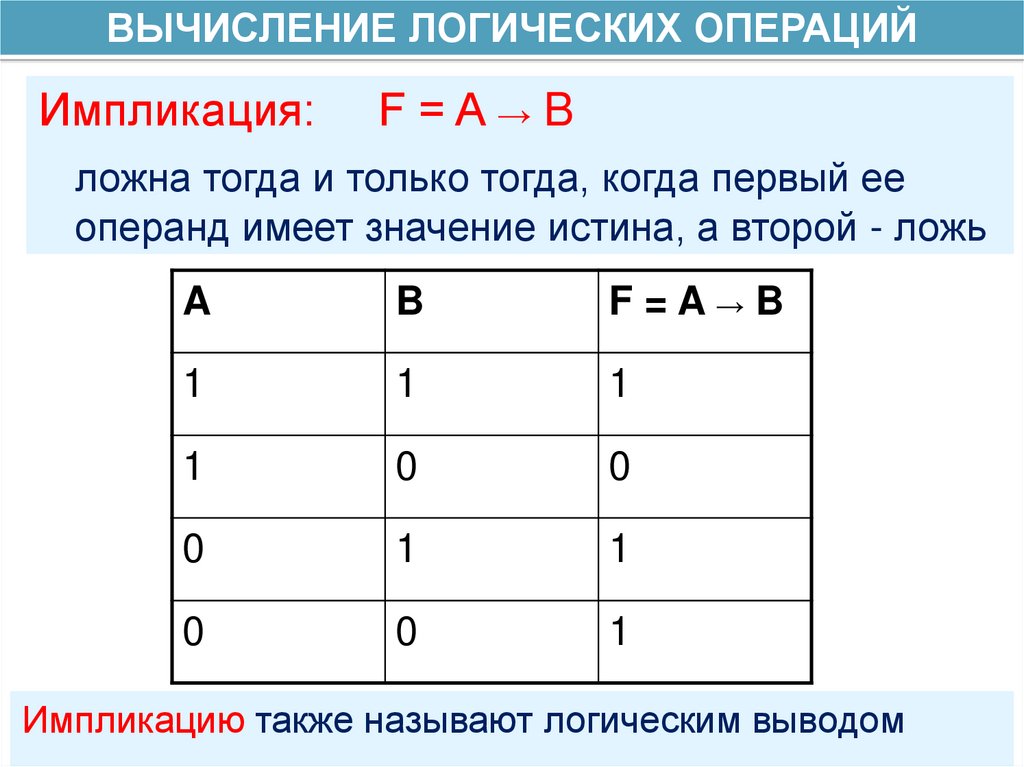
ВЫЧИСЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАЦИЙИмпликация:
F=A→B
ложна тогда и только тогда, когда первый ее
операнд имеет значение истина, а второй - ложь
A
B
F=A→B
1
1
1
1
0
0
0
1
1
0
0
1
Импликацию также называют логическим выводом
9.
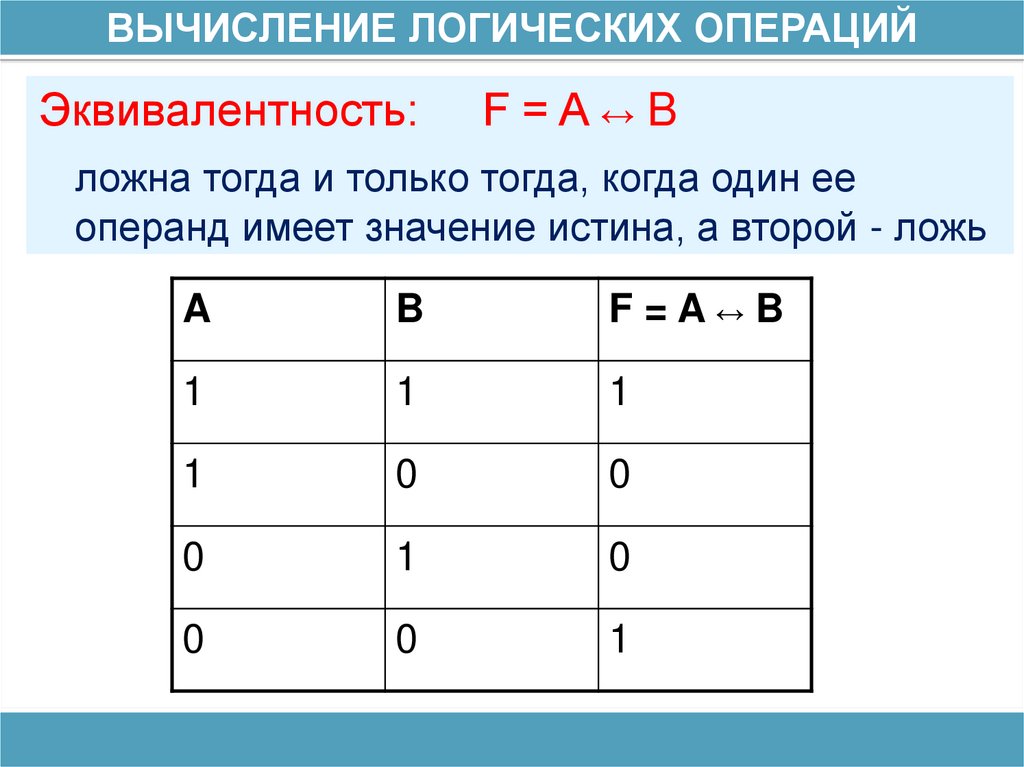
ВЫЧИСЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАЦИЙЭквивалентность:
F=A↔B
ложна тогда и только тогда, когда один ее
операнд имеет значение истина, а второй - ложь
A
B
F=A↔B
1
1
1
1
0
0
0
1
0
0
0
1
10.
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕЛогическое выражение – это правильно
построенная последовательность логических
переменных и логических значений,
соединенных знаками логических операций, в
котором таже могут использоваться скобки для
изменения приоритета операций.
Примеры логических выражений:
A V(B Λ D )
¬(1 Λ D ) → Z
(А=C) V A Λ (B V ¬C)
11.
ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕИндуктивное определение логических выражений
(1) <логическое выражение> : := <логическое значение> |
< логическая переменная> | (< логическое
выражение>) |
< одноместная логическая операция> < логическое
выражение> |
< логическое выражение> < двуместная логическая
операция> < логическое выражение >
(2) < логическое значение > : := 0 |1
(3)< логическая переменная > : := А | B | C | D | E | G | H |
…|Z
(4)< одноместная логическая операция > : := ¬
(5)< двуместная логическая операция > : := V | Λ | → | ↔
12.
ПРИОРИТЕТНОСТЬ ЛОГИЧЕСКИХ ОПЕРАЦИЙПорядок выполнения логических операций в
логическом выражении:
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
Для изменения порядка выполнения логических операций
используются скобки
Примеры:
Λ (B V D ) порядка
A Λвыполнения
BVD
Для измененияAуказанного
2
1
2
логических операций
используются1 скобки
¬(D V 1 ) → Z
¬D V 1 → Z
2
1
1
3
2
3
13.
ЗАКОНЫ ЛОГИКИЗаконы де Моргана
¬ (А V B) = ¬А Λ ¬ B
¬ (А Λ B) = ¬А V ¬ B
Закон отрицание отрицания (двойного отрицания)
¬(¬А)=A
Закон исключенного третьего
A V ¬А=1
Закон противоречия (непротиворечия)
A Λ ¬А=0
14.
ЗАКОНЫ ЛОГИКИИмпликацию можно выразить
через дизъюнкцию и отрицание:
А → В = ¬A v В
Эквивалентность можно выразить
через отрицание, дизъюнкцию и конъюнкцию:
А ↔ В = (¬A v В) Λ (¬ В v А)
Исключающее ИЛИ (ХОR) можно выразить
через отрицание, дизъюнкцию и конъюнкцию :
A ⊻ B = ((A ∧ ¬ B) ⋁ (¬ A ∧ B))
15.
ЗАКОНЫ ЛОГИКИЗакон дистрибутивности (распределительный) :
для дизъюнкции (логического сложения):
(А V B) Λ C = (A Λ C) V (B Λ C)
для конъюнкции (логического умножения):
(A Λ B) V C = (A V C) Λ (B V C)
Закон идемпотентности (равносильности):
для дизъюнкции:
АVA=A
для конъюнкции:
AΛA=A
16.
ЗАКОНЫ ЛОГИКИЗакон коммутативности:
для логического сложения:
для логического умножения:
АVB=BVA
A Λ B = B Λ A.
Закон ассоциативности :
для дизъюнкции (логического сложения):
(А V B) V C = A V (B V C)
для конъюнкции (логического умножения):
(A Λ B) Λ C = A Λ (B Λ C)
17.
ЗАКОНЫ ЛОГИКИЗаконы исключения констант в логическом
выражении для дизъюнкции:
АV1=1
АV0=A
для конъюнкции:
AΛ 1 =A
AΛ 0 = 0
Закон поглощения:
для дизъюнкции: А V (A Λ B) = A;
для конъюнкции : A Λ (A V B) = A.
18.
УПРОЩЕНИЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙЗаконы логики используются для упрощения
логических выражений.
Упрощение логических выражений заключается в
следующием:
─ убрать все скобки;
─ уменьшить количество операций в выражении;
─ уменьшить количество операндов в
выражении.
Например: (A V С Λ A) Λ (BVC) = A Λ B V A ΛC
19.
УПРОЩЕНИЕ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙПример 1. Упростить выражение (А V В) Λ (А V С).
Решение:
Раскроем скобки:
(А V В) Λ (А V С) =А Λ (А V С) V В Λ (А V С) =
=A Λ A V A Λ C V B Λ A V B Λ C
По закону идемпотентности A Λ A =A, следовательно:
AΛAVAΛ C V BΛAV BΛ C =AVAΛ C V BΛAV BΛ C
В выражениях А и А Λ C вынесем за скобки А и, используя
свойство 1 V С= 1 и AΛ1 =A получим
A V A Λ C V B Λ A V B Λ C = A Λ (1 V C) V B Λ A V B Λ C =
= A V B Λ A V B Λ C (или тут можно применить сразу
применить закон поглощения: A V A Λ C = A )
Аналогично предыдущему пункту вынесем за скобки А (или
применим закон поглощения A V B Λ A = A).















 informatics
informatics








