Логические основы компьютера

1.

ЛОГИЧЕСКИЕ ОСНОВЫ КОМПЬЮТЕРА.
ФОРМЫ МЫШЛЕНИЯ
АЛГЕБРА ЛОГИКИ
ПОСТРОЕНИЕ ТАБЛИЦ
ИСТИННОСТИ. ЗАКОНЫ ЛОГИКИ
БАЗОВЫЕ ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
КОМПЬЮТЕРА

2.

Логика
Логика – это наука о формах и способах мышления.
Первые учения о формах и способах мышления возникли в Древнем
Китае и Индии. Основоположником формальной логики является
Аристотель.
Аристотель (384-322 до н.э.). Основоположник
формальной логики (понятие, суждение, умозаключение).
Джордж Буль (1815-1864). Создал новую область
науки - Математическую логику (Булеву алгебру или
Алгебру высказываний).
Клод Шеннон (1916-2001). Его исследования
позволили применить алгебру логики в
вычислительной технике

3.

Формы мышления
Мышление всегда осуществляется через понятия, высказывания и
умозаключения.
Понятие - это форма мышления, которая выделяет существенные
признаки предмета или класса предметов, позволяющие отличать их от
других.
Высказывание - это формулировка своего понимания окружающего
мира. Высказывание является повествовательным предложением, в
котором что-либо утверждается или отрицается. По поводу
высказывания можно сказать, истинно оно или ложно.
Умозаключение - это форма мышления, с помощью которой из одного
или нескольких суждений может быть получено новое суждение.

4.

Понятие
Существенными называются такие признаки, каждый из которых, взятый отдельно,
необходим, а все вместе достаточны, чтобы с их помощью отличить данный
предмет от всех остальных и сделать обобщение, объединив однородные
предметы в множество.
Примеры понятий:
•Единичные понятия: самая высокая гора в Европе, этот стол, Москва и т.д.
•Общие понятия: красота, металл, доброта, глупость, лес, коллектив и т.д.
•Абстрактные понятия: вес, жесткость, цвет, вселенная, человечество и т.д.
•Конкретные понятия: круг, дом, пламя, битва и т.д.
Рядом с названием предмета перечислены его признаки. Какие из них являются
существенными для данного предмета?
А) Ученик - высокий; умный; одет в форму; на спине - ранец; посещает школу;
любит книги; много знает; овладевает знаниями; учится; веселый.
Б) Ромашка - полевой цветок; имеет белые лепестки и желтую середину;
лекарственное растение; неприхотливый цветок; цветок, растущий у дороги.

5.

Понятие
Любое понятие характеризуется содержанием и объемом.
Содержание понятия - совокупность (множество) его признаков. Среди
признаков предмета есть существенные и второстепенные. Содержание понятия
может меняться в зависимости от знаний, от точки зрения и т.д. Например, для
обычного человека содержанием понятия "вода" являются следующие ее
признаки: прозрачная, жидкая, безвкусная, ее пьют, утоляя жажду. Для химика
вода - вещество, содержащее водород и кислород, компонент многих реакций.
Объем понятия - множество предметов, к которым прилагается понятие.
Например,
объем
понятия
"четырехугольник":
параллелограмм,
ромб,
прямоугольник, квадрат, трапеция. Между объемом и содержанием понятия
существует
важное
соотношение:
при
увеличении
содержания
уменьшается его объем и наоборот.
Расположите и запишите понятия в порядке расширения их объемов:
насекомое,
живое существо,
комар.
Комар, насекомое,
живое существо.
понятия

6.

Высказывание
Высказывание (суждение) - это предложение на любом языке,
содержание которого можно однозначно определить как истинное или
ложное.
В русском языке
предложениями:
высказывания
выражаются
повествовательными
Земля вращается вокруг Солнца.
Москва - столица.
Но не всякое повествовательное предложение является высказыванием:
Это высказывание ложное.
Побудительные и вопросительные предложения высказываниями не
являются.
Без стука не входить!
Откройте учебники.
Ты выучил стихотворение?

7.

Высказывание или нет?
Зимой идет дождь.
Снегири живут в Крыму.
Кто к нам пришел?
У треугольника 5 сторон.
Как пройти в библиотеку?
Переведите число в десятичную систему.
Запишите домашнее задание

8.

Высказывание
в математической логике – утверждение, истинность которого (в общем случае)
зависит от значений входящих в него переменных.
Высказывания
Частные
(3>5)
Истинные
(1=1)
Общие
(y>5)
Ложные
(-5<-10)
Тождественно
истинные
(x2+1)>0
Тождественно
ложные
( (x2+y2)<0 )
Зависящие
от условий
(x+y<0)

9.

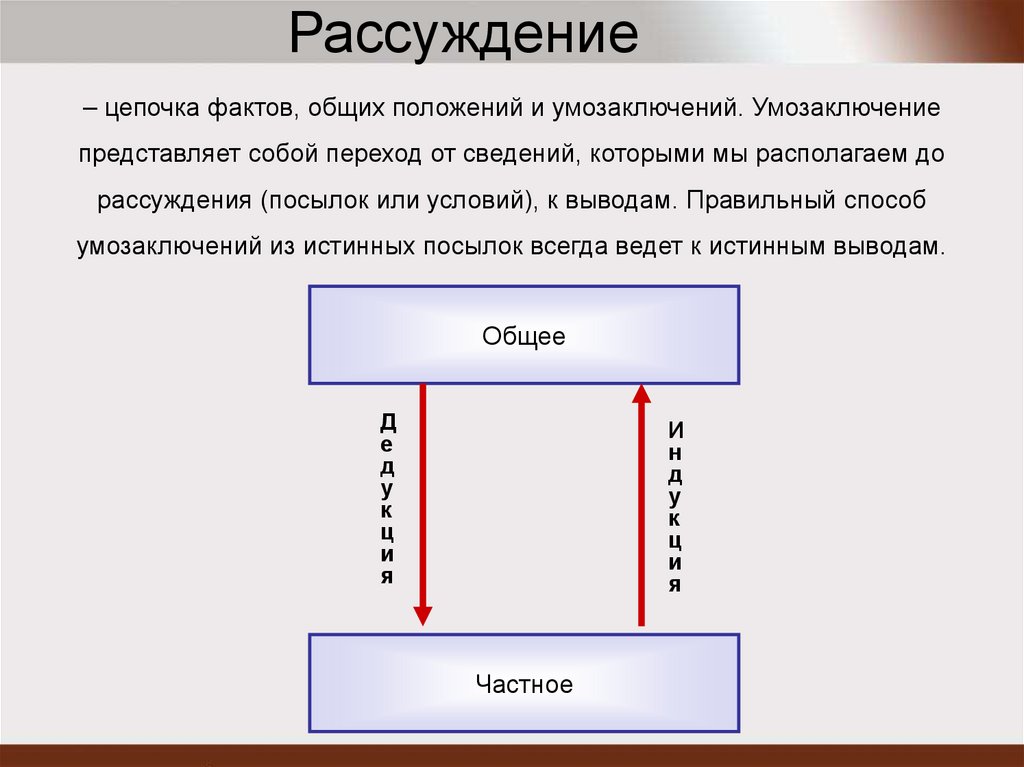
Рассуждение
– цепочка фактов, общих положений и умозаключений. Умозаключение
представляет собой переход от сведений, которыми мы располагаем до
рассуждения (посылок или условий), к выводам. Правильный способ
умозаключений из истинных посылок всегда ведет к истинным выводам.
Общее
Д
е
д
у
к
ц
и
я
И
н
д
у
к
ц
и
я
Частное

10.

11.

Алгебра логики
Алгебра логики определяет правила записи, вычисления значений,
упрощения и преобразования высказываний.
В алгебре логики высказывания обозначают буквами и называют
логическими переменными.
Если
высказывание
истинно,
то
значение
соответствующей
ему
логической переменной обозначают единицей (А = 1), а если ложно - нулём
(В = 0).
0 и 1 называются логическими значениями.

12.

Простые и сложные высказывания
Высказывания бывают простые и сложные.
Высказывание называется простым, если никакая его часть сама не
является высказыванием.
Сложные (составные) высказывания строятся из простых с помощью
логических операций.
Название логической операции
Логическая связка
Инверсия (логическое отрицание)
«не»; «неверно, что»
Дизъюнкция (логическое сложение)
«или»
Конъюнкция (логическое умножение)
«и»; «а»; «но»; «хотя»
Импликация (логическое следование)
если – то;
Эквивалентность (логическая равнозначность)
тогда, и только тогда
Логические операции имеют следующий приоритет:
инверсия, конъюнкция, дизъюнкция, импликация, эквивалетность

13.

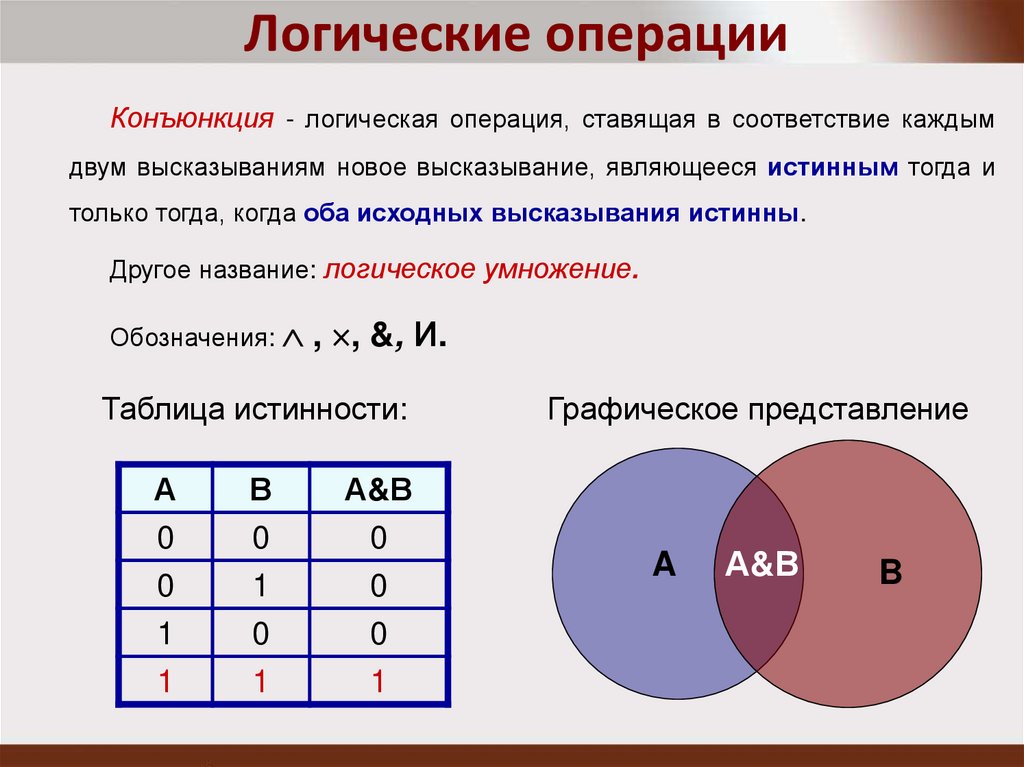
Логические операции
Конъюнкция - логическая операция, ставящая в соответствие каждым
двум высказываниям новое высказывание, являющееся истинным тогда и
только тогда, когда оба исходных высказывания истинны.
Другое название: логическое умножение.
Обозначения:
, , &, И.
Таблица истинности:
А
В
А&В
0
0
0
0
1
0
1
0
0
1
1
1
Графическое представление
A
А&В
B

14.

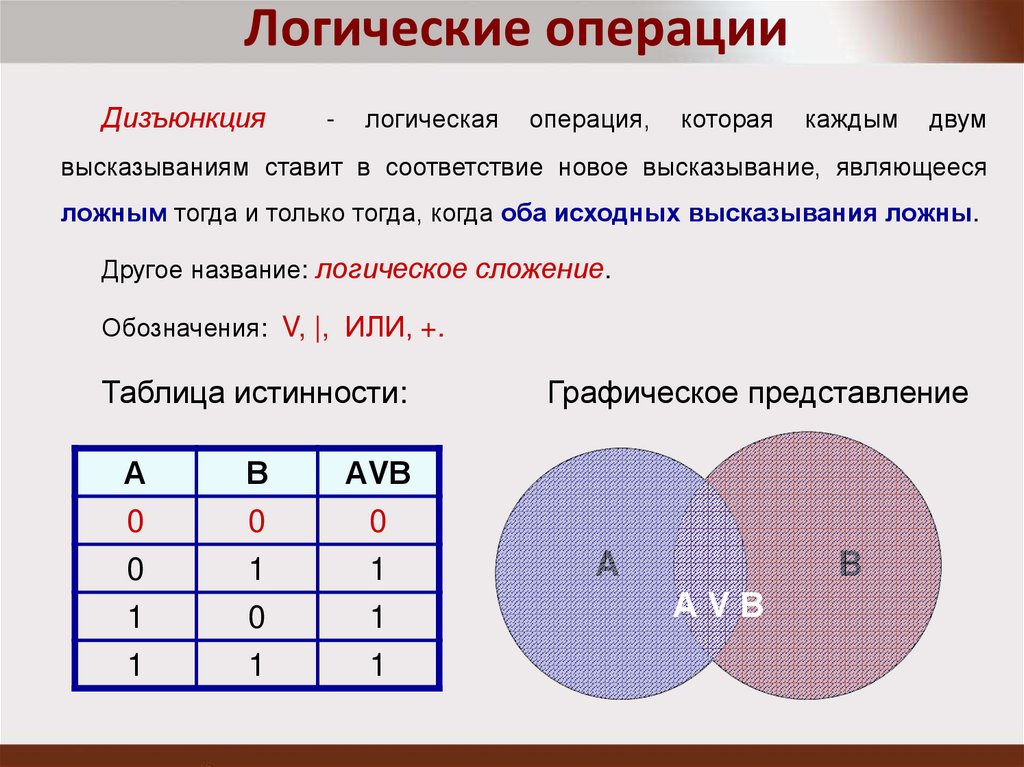
Логические операции
Дизъюнкция
-
логическая
операция,
которая
каждым
двум
высказываниям ставит в соответствие новое высказывание, являющееся
ложным тогда и только тогда, когда оба исходных высказывания ложны.
Другое название: логическое сложение.
Обозначения: V, |, ИЛИ, +.
Таблица истинности:
А
В
АVВ
0
0
0
0
1
1
1
0
1
1
1
1
Графическое представление
B
A
АVВ

15.

Логические операции
Инверсия - логическая операция, которая каждому высказыванию
ставит в соответствие новое
противоположно исходному.
высказывание,
значение
которого
Другое название: логическое отрицание.
Обозначения: НЕ, ¬ , ¯ .
Таблица истинности:
А
Ā
0
1
1
0
Графическое представление
Ā
A

16.

Логические операции
Импликация – это логическая операция, ставящая в соответствие каждым
двум
простым
высказываниям
составное
высказывание,
являющееся
ложным тогда и только тогда, когда условие (первое высказывание)
истинно, а следствие (второе высказывание) ложно.
В естественном языке – «Если A, то B»;
Обозначение –
→
Таблица истинности:
А
В
А В
0
0
1
0
1
1
1
0
0
1
1
1
Графическое представление
А
B A B

17.

Логические операции
Логическая эквивалентность (равнозначность) – это логическая операция,
ставящая в соответствие каждым двум высказываниям составное высказывание,
являющееся истинным тогда и только тогда, когда оба исходных высказывания
одновременно истины или одновременно ложны.
В естественном языке – «Тогда и только тогда и в том и только том случае»;
Обозначение –
↔
Таблица истинности:
А
В
А↔В
0
0
1
0
1
0
1
0
0
1
1
1
Графическое представление
A↔B
AA
B
B

18.

Построение таблиц истинности для логических
выражений
подсчитать n - число переменных в выражении
подсчитать общее число логических операций в выражении
установить последовательность выполнения логических операций
определить число столбцов в таблице
заполнить шапку таблицы, включив в неё переменные и операции
определить число строк в таблице без шапки: m =2n
выписать наборы входных переменных
провести заполнение таблицы по столбцам, выполняя логические
операции в соответствии с установленной последовательностью

19.

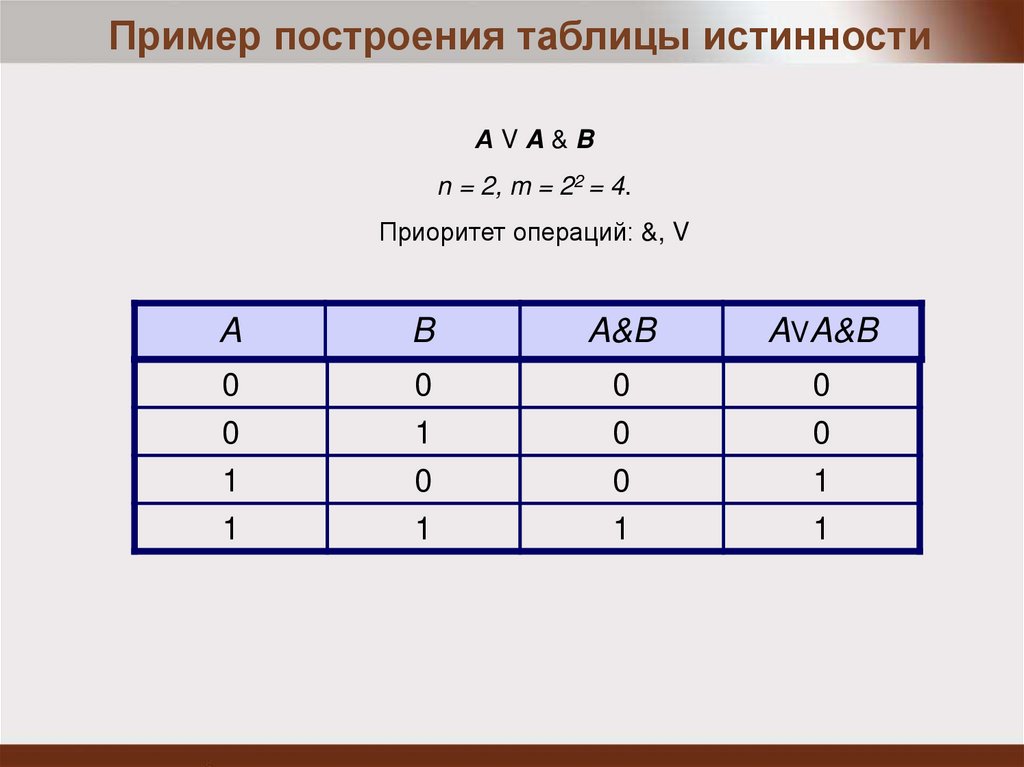
Пример построения таблицы истинности
АVA&B
n = 2, m = 22 = 4.
Приоритет операций: &, V
A
B
A&B
AVA&B
0
0
0
0
0
1
0
0
1
0
0
1
1
1
1
1

20.

Свойства логических операций
Законы алгебры-логики
Закон исключения
Переместительный
третьего
A&
AB
&=
ĀB
=&
0A
AV
AB
V=
ĀB
=V
1A
(A & B) &
AC
& =AA= &
A ( B & C)
Закон
Сочетательный
повторения
(A V B) V
AC
VA
=A=VA( B V C)
Законы операций
Распределительный
с0и1
A&(BVC)=
A & 0=0;(A&B)
A &1V=(A&C)
A
A V 0 = =A;(AVB)&(AVC)
AV1=1
AV(B&C)
Закон
Законы
двойного
общей
отрицания
инверсии
A&B=ĀVB
Ā=A
AVB =Ā&B

21.

Доказательство закона
Распределительный закон для логического сложения:
A v (B & C) = (A v B) & (A v C).
A
B
C
B&C
A v (B & C)
AvB
AvC
(A v B) & (A v C)
0
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
1
0
0
0
1
0
0
0
1
1
1
1
1
1
1
1
0
0
0
1
1
1
1
1
0
1
0
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
1
1
1
1
Складываем
Умножаем
Умножаемвыделенных
(АvB)
ВА
наи С(В&С)
В
C
наии(AvC
выводим
выводим
и выводим
)и выводим
результат.
результат.
результат.
результат.
Равенство
столбцов
доказывает
распределительный закон.

22.

Решение логических задач
Задача. Коля, Вася и Серёжа гостили летом у бабушки. Однажды один
из мальчиков нечаянно разбил любимую бабушкину вазу.
На вопрос, кто разбил вазу, они дали такие ответы:
Серёжа: 1) Я не разбивал. 2) Вася не разбивал.
Вася:
3) Серёжа не разбивал. 4) Вазу разбил Коля.
Коля:
5) Я не разбивал. 6) Вазу разбил Серёжа.
Бабушка знала, что один из её внуков
(правдивый), оба раза сказал правду; второй
(шутник) оба раза сказал неправду; третий
(хитрец) один раз сказал правду, а другой раз неправду. Назовите имена правдивого, шутника
и хитреца.
Кто из внуков разбил вазу?

23.

Решение.
Пусть К =«Коля разбил вазу», В =«Вася разбил вазу», С =«Серёжа разбил вазу».
Представим в таблице истинности высказывания каждого мальчика. Так как
ваза разбита одним внуком, составим не всю таблицу, а только её фрагмент,
содержащий наборы входных переменных: 001, 010, 100.
K
B
C
Утверждение
Серёжи
С
В
Утверждение
Васи
Утверждение
Коли
С
K
К
C
0
0
1
0
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
0
1
1
1
1
0
0
Исходя из того, что знает о внуках бабушка, следует искать в таблице строки,
содержащие в каком-либо порядке три комбинации значений: 00, 11, 01 (или 10).
Это первая строка.
Вазу разбил Серёжа, он - хитрец. Шутником оказался Вася. Имя правдивого
внука - Коля.

24.

Упрощение логических выражений
Упростить логическое выражение до 3-х простейших операций:
(( A B C ) C ) ( A B C )
Справка
1). X Y = ¬X v Y
2). Преобразуем ¬X:
Х
Y
( A B C) C ( A B C) C ( A B C) C
( A B C) A B C A B C A B C A (B C)
( A B C A ( B C )) C ( A B C ) C A B C A C
=0
A B C A C A C ( B 1) A C
(5)
(6)
( 12, 16 )
( 15, 16 )
Аналогично для Y:
( A B C ) ( A B) C A B C A C B C A B C
X Y= A C A C B C A B C C ( A A B) A B C
C A B C C A B
=1
( 10 )

25.

Решение логических задач упрощением
логических выражений
На соревнованиях по легкой атлетике Андрей, Боря, Сережа и Володя
заняли первые четыре места. Но когда девочки стали вспоминать, как эти
места распределились между победителями, то мнения разошлись:
Даша: Андрей был первым, а Володя – вторым.
Галя: Андрей был вторым, а Борис – третьим.
Лена: Боря был четвертым, а Сережа – вторым.
Известно, что каждая девочка в одном утверждении ошиблась, а в другом
была права. Кто из мальчиков какое место занял?
Введем обозначения:
А1 – Андрей первый, В2 – Володя второй,
А2 – Андрей второй, Б3 – Борис третий,
Б4 – Борис четвертый, С2 – Сережа второй

26.

Решение логических задач упрощением
логических выражений
Условие того, что в каждом утверждении одно высказывание истинно, а другое ложно:
X Y 1
преобразуем
X Y X Y 1;
Запишем это условие для высказываний каждой девочки:
А1 В 2 1;
А2 Б 3 1;
Б 4 С 2 1;
Тогда логическое произведение всех трех выражений = 1;
А1 В2 А2 Б 3 Б 4 С 2 1;
После преобразований:
( А1 В 2 А1 В 2) ( А2 Б 3 А2 Б 3) ( Б 4 С 2 Б 4 С 2) 1;
Так как один и тот же человек не может занять разные места, и разные спортсмены не
могут находиться на одном месте, получим из первых 2-х скобок:
( А1 В 2 А2 Б 3 А1 В 2 А2 Б 3 А1 В 2 А2 Б 3 А1 В 2 А2 Б 3)
Полученный результат умножим логически на 3-ю скобку:
( А1 В 2 А2 Б 3 А1 В 2 А2 Б 3) ( Б 4 С 2 Б 4 С 2) 1;
Ответ:
Сергей
А1=1;
– третий,
Б3=1; С2=1;
Володя
=>- В4=1
четвертый
А1 Андрей
В 2 А2– первый,
Б3 Б 4
С 2 1;– второй, Борис

27.

Дополнительный справочный материал
1).
A A
2).
A B A B
3).
A B A B
4).
A B A B
5).
A B A B
6).
A B ( A B) ( A B) ( A B) ( A B)
7).
A ( A B) A
8).
A A B A
9).
A ( A B) A B
10).
A A B A B
11).
Законы коммутативности :
( A B) B A;
12).
Законы
A B B A
ассоциативности :
( A B) C A ( B C );
13).
Законы
A A A;
14).
Законы
( A B) C A ( B C )
и демпотентности :
A A A
д истрибутивности :
A ( B C ) ( A B) ( A C );
15).
A 1 1;
A 1 A;
16.
A 0 0;
A A 0
A ( B C ) ( A B) ( A C )
A A 1

28.

Базовые
логические элементы
компьютера

29.

ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Дискретный преобразователь, который после обработки входных двоичных
сигналов выдает на выходе сигнал, являющийся значением одной из
логических операций, называется логическим элементом.
Базовые логические элементы реализуют три базовые логические
операции:
логический элемент «И» (конъюнктор) – логическое умножение;
логический элемент «ИЛИ» (дизъюнктор) – логическое сложение;
логический элемент «НЕ» (инвертор) – логическое отрицание.
Любая логическая операция может быть представлена в виде комбинации
трех базовых, поэтому любые устройства компьютера, производящие
обработку и хранение информации, могут быть собраны из базовых
логических элементов.
Логические элементы компьютера оперируют с сигналами,
представляющими собой электрические импульсы.

30.

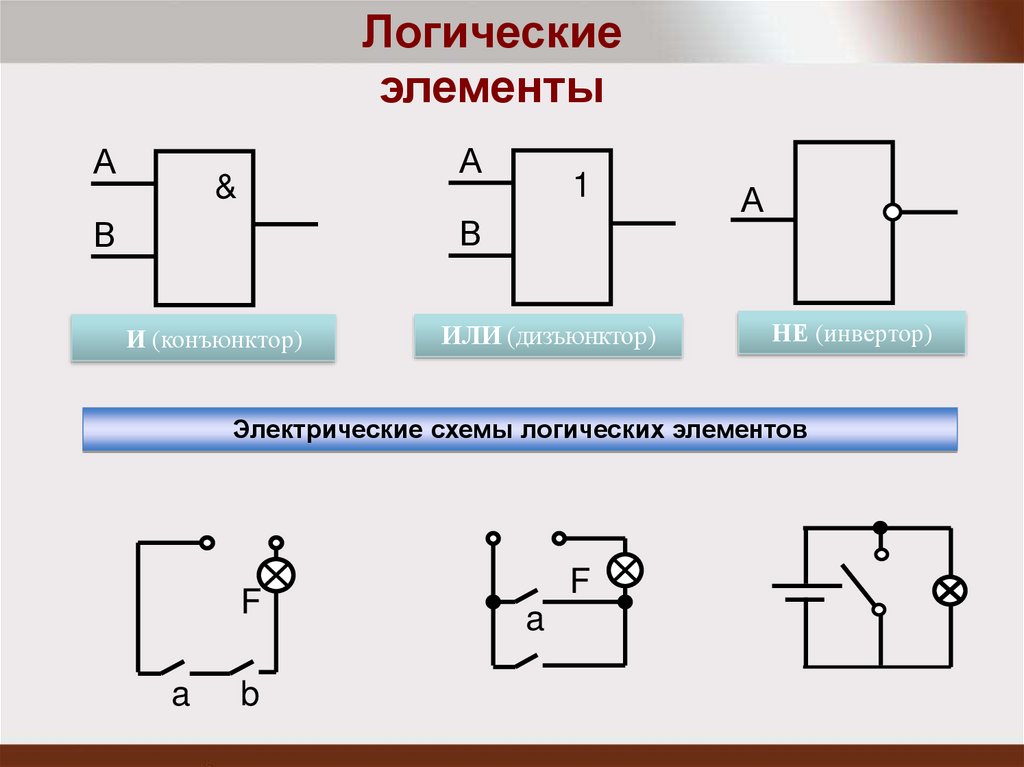
Логические
элементы
А
А
&
1
В
В
И (конъюнктор)
ИЛИ (дизъюнктор)
А
НЕ (инвертор)
Электрические схемы логических элементов
F
a
b
F
a

31.

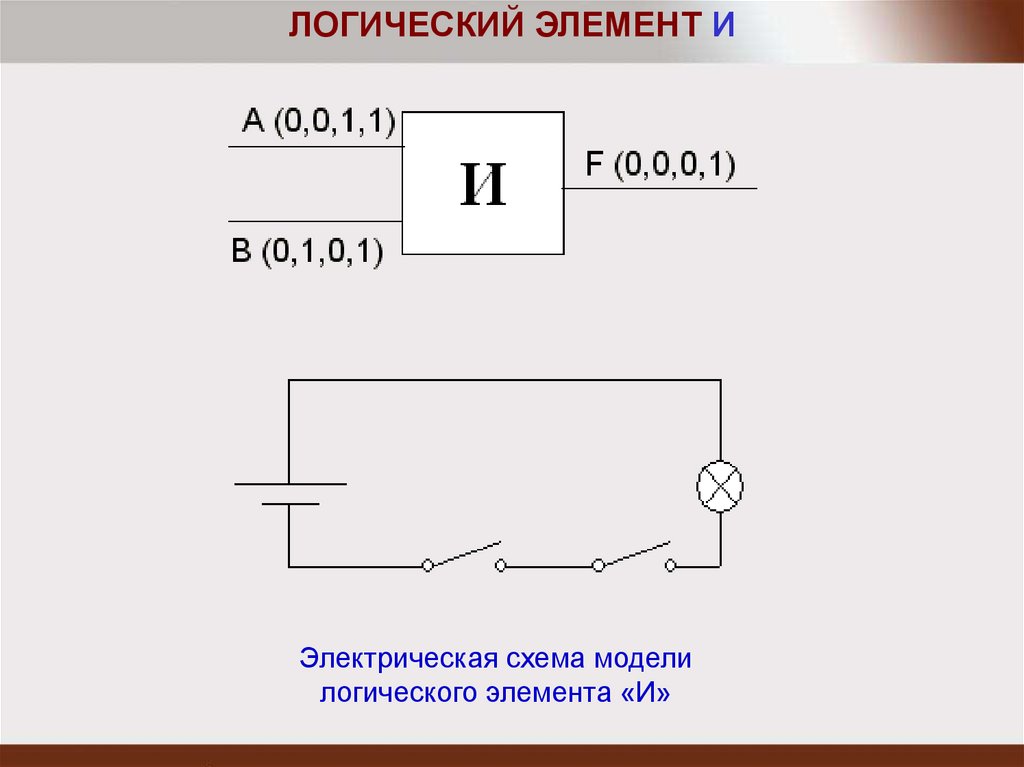
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ И
Электрическая схема модели
логического элемента «И»

32.

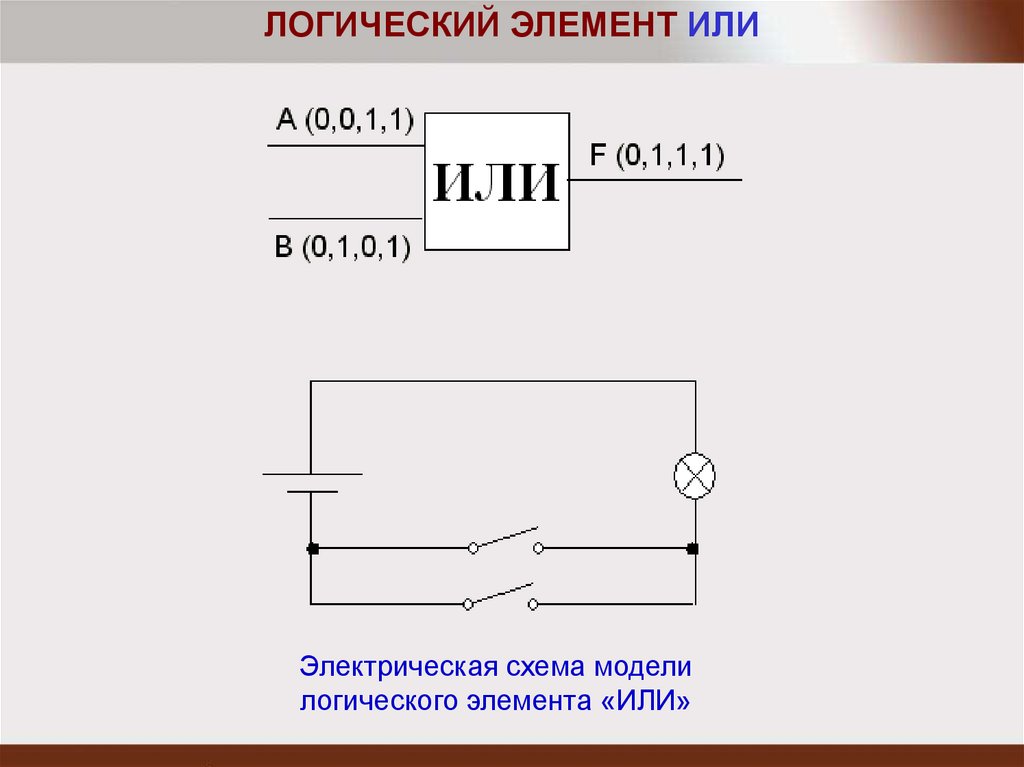
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ ИЛИ
Электрическая схема модели
логического элемента «ИЛИ»

33.

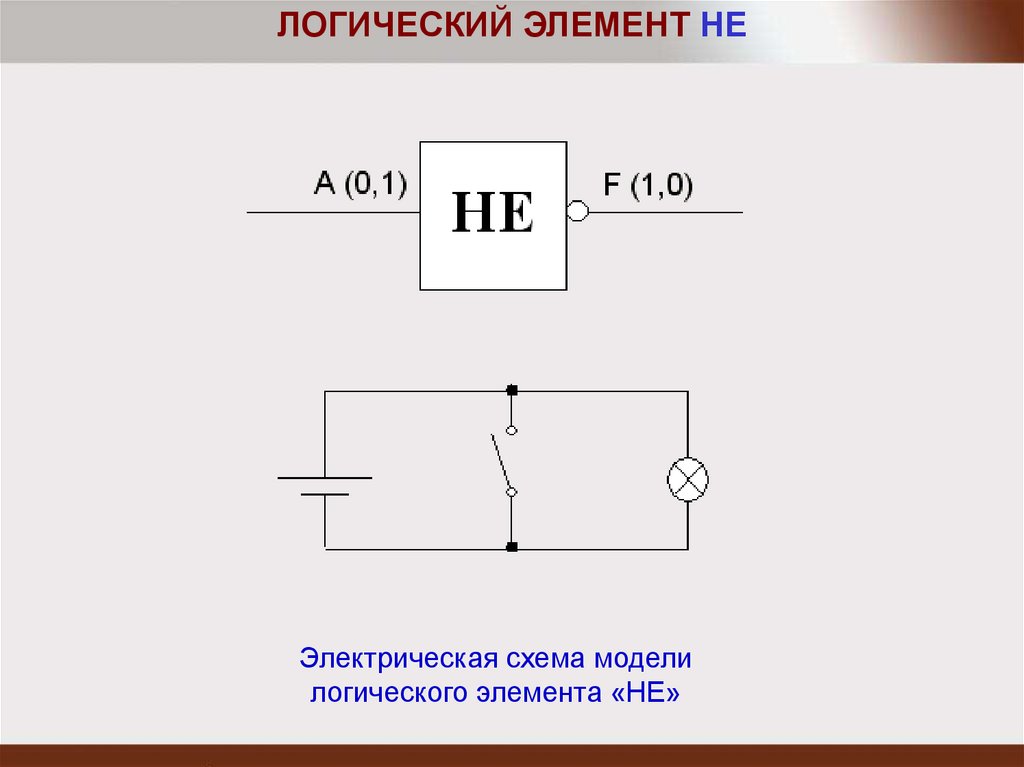
ЛОГИЧЕСКИЙ ЭЛЕМЕНТ НЕ
Электрическая схема модели
логического элемента «НЕ»

34.

Анализ электронной схемы
Какой сигнал
бытькомбинации
на выходе при
каждомна
возможном
Решение.
Вседолжен
возможные
сигналов
входах А инаборе
В внесём в
сигналовистинности.
на входах? Проследим преобразование каждой пары сигналов
таблицу
при прохождении их через логические элементы и запишем полученный
результат в таблицу. Заполненная таблица истинности полностью
описывает рассматриваемую электронную схему.
А 0010
В 0101
&
0010 F
1010
A
B
F
0
0
0
0
1
0
1
0
1
0
1
0
В инвертор поступает сигнал от входа В.
В конъюнктор поступают сигналы от входа А и от инвертора. Таким
образом, F = A & B.

35.

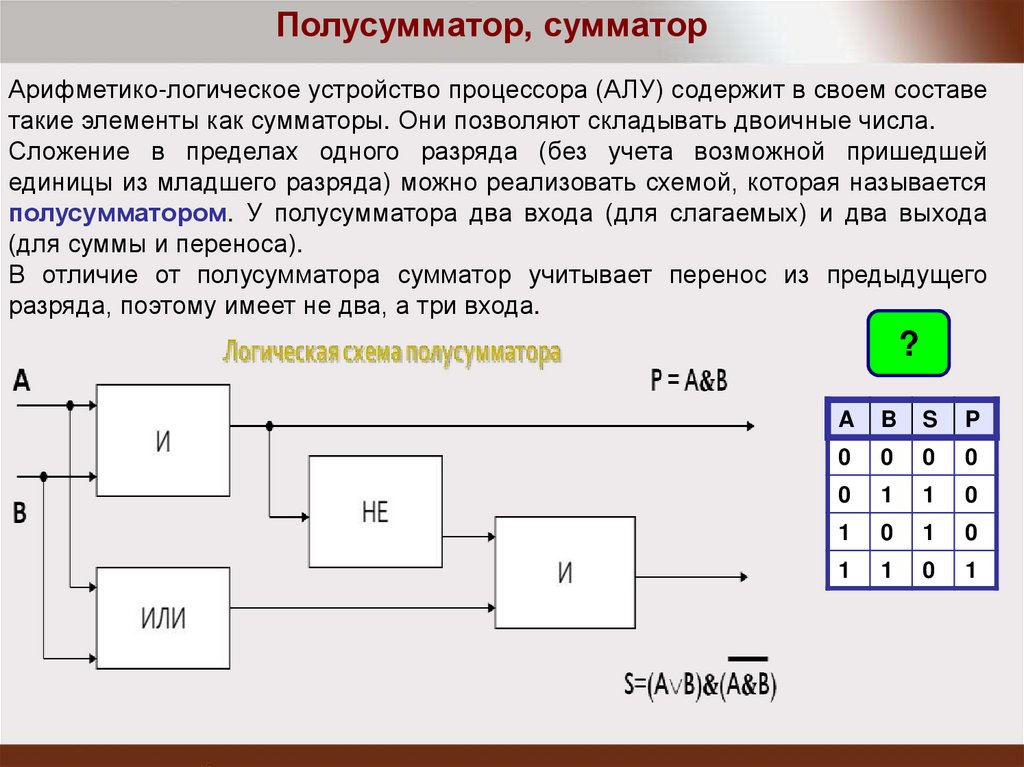
Полусумматор, сумматор
Арифметико-логическое устройство процессора (АЛУ) содержит в своем составе
такие элементы как сумматоры. Они позволяют складывать двоичные числа.
Сложение в пределах одного разряда (без учета возможной пришедшей
единицы из младшего разряда) можно реализовать схемой, которая называется
полусумматором. У полусумматора два входа (для слагаемых) и два выхода
(для суммы и переноса).
В отличие от полусумматора сумматор учитывает перенос из предыдущего
разряда, поэтому имеет не два, а три входа.
?
A
B
S
P
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1

36.

Триггер
(trigger - защелка, спусковой крючок) - это устройство, позволяющее
запоминать, хранить и считывать информацию.
Каждый триггер хранит 1 бит информации, т.е он может находиться в одном из
двух устойчивых состояний — логический «0» или логическая «1».
Триггер способен почти мгновенно переходить из одного электрического
состояния в другое и наоборот.
Логическая схема триггера выглядит следующим образом:
Входы триггера расшифровываются следующим образом — S (от английского Set установка) и R (Reset - сброс). Они используются для установки триггера в
единичное состояние и сброса в нулевое. В связи с этим такой триггер называется
RS-триггер.
Выход Q называется прямым, а противоположный — инверсный. Сигналы на
прямом и инверсном выходах, конечно же, должны быть противоположны.
Q
Q

37.

Триггер
Пусть для определенности на вход S подан единичный сигнал, a R=0. Тогда независимо
от состояния другого входа, который подсоединен к выходу Q (иначе говоря, вне
зависимости от предыдущего состояния триггера), верхний по схеме элемент ИЛИ-НЕ
получит на выходе 0 (результат ИЛИ равен 1, но его инверсия - 0). Этот нулевой сигнал
передается на вход другого логического элемента, где на втором входе R тоже
установлен 0. В итоге после выполнения логических операций ИЛИ-НЕ над двумя
входными нулями этот элемент получает на выходе 1, которую возвращает первому
элементу на соответствующий вход. Последнее обстоятельство очень важно: теперь,
когда на этом входе установилась 1, состояние другого входа (S) больше не играет
роли. Иными словами, если даже теперь убрать входной сигнал S, внутреннее
распределение уровней сохранится без изменения.
Поскольку Q = 1, триггер перешел в единичное
состояние, и, пока не придут новые внешние сигналы,
сохраняет его. Итак, при подаче сигнала на вход S
триггер переходит в устойчивое единичное состояние.
Q
Q
При противоположной комбинации сигналов R = 1 и S = 0 вследствие полной
симметрии схемы все происходит совершенно аналогично, но теперь на выходе
Q уже получается 0. Иными словами, при подаче сигнала на R-триггер
сбрасывается в устойчивое нулевое состояние.
Таким образом окончание действия сигнала в обоих случаях приводит к тому, что
R = 0 и S = 0.