Основы логики и логические основы компьютера

1.

Основы логики и логические
основы компьютера

2.

Первые учения о формах и способах рассуждений возникли в странах
Древнего Востока (Китай, Индия).
В основе современной логики лежат учения, созданные
древнегреческими мыслителями.
Формы мышления
Основы формальной логики заложил Аристотель, который впервые
отделил логические формы мышления (речи) от его содержания.
Логика — это наука о формах и способах мышления.
Законы логики отражают в сознании человека свойства, связи и отношения
объектов окружающего мира. Логика позволяет строить формальные
модели окружающего мира, отвлекаясь от содержательной стороны.
Основными формами мышления являются понятие, высказывание и
умозаключение.

3.

Понятие
Понятие - это форма мышления, фиксирующая основные,
существенные признаки объекта, выделяющие, отличающие его от
других объектов.
Объекты, объединенные понятием, образуют некоторое множество.
«компьютер» «автомобиль»
Содержание понятия совокупность существенных
признаков объекта.
Содержание понятия
«персональный компьютер»:
«Персональный компьютер —
это универсальное электронное
устройство для автоматической
обработки информации,
предназначенное для одного
пользователя».
Объем понятия определяется
совокупностью предметов, на
которую оно распространяется.
Объем понятия «персональный
компьютер» выражает всю
совокупность (сотни миллионов)
существующих в настоящее
время в мире персональных
компьютеров.

4.

Высказывание
Свое понимание окружающего мира человек формулирует в форме
высказываний (суждений, утверждений).
Высказывание строится на основе понятий и по форме является
повествовательным предложением. Не может быть повелительным или
вопросительным предложением, т.к. оценка его истинности или ложности
невозможна.
Естественный язык: «Два умножить на два равно четырем»
Формальный язык: «2 • 2 = 4».
Истинное высказывание (true): связь понятий правильно отражает
свойства и отношения реальных вещей. «Процессор является устройством
обработки информации».
Ложное высказывание (false): не соответствует реальной
действительности. «Процессор является устройством печати».
Высказывание — это форма мышления, в которой что-либо утверждается
или отрицается о свойствах реальных предметов и отношениях между ними
(истина или ложь).
На основании простых высказываний могут быть построены составные
высказывания. «Процессор является устройством обработки информации и
принтер является устройством печати»
Иногда истинность высказывания является относительной (компьютер).

5.

Умозаключение.
Умозаключение – это форма мышления, с помощью которой из одного
или нескольких суждений (посылок) может быть получено новое суждение
(заключение).
«Все углы треугольника равны»
«Этот треугольник равносторонний»
Посылками умозаключения по правилам формальной логики могут
быть только истинные суждения.
Если умозаключение проводится в соответствии с правилами формальной
логики, то оно будет истинным. В противном случае можно прийти к
ложному умозаключению.

6.

Алгебра высказываний
Алгебра высказываний была разработана для того, чтобы можно было
определить истинность или ложность высказываний не вникая в их содержание.
«Отцом» алгебры высказываний является Джордж Буль
Суждения (простые высказывания) - логические переменные
А = «Два умножить на два равно четырем».
В = «Два умножить на два равно пяти».
В алгебре высказываний высказывания обозначаются именами
логических переменных, которые могут принимать лишь два
значения: «истина» (1) и «ложь» (0). Логические константы
Истина — 1 (А = 1)
Ложь — 0 (В = 0)
Логическая переменная: символически обозначенная логическая величина,
которая может принимать значение ИСТИНА или ЛОЖЬ.
Логическое выражение: простое или сложное высказывание.
Для образования сложных высказываний используются базовые
логические операции, выражаемые с помощью логических связок «и»,
«или», «не».

7.

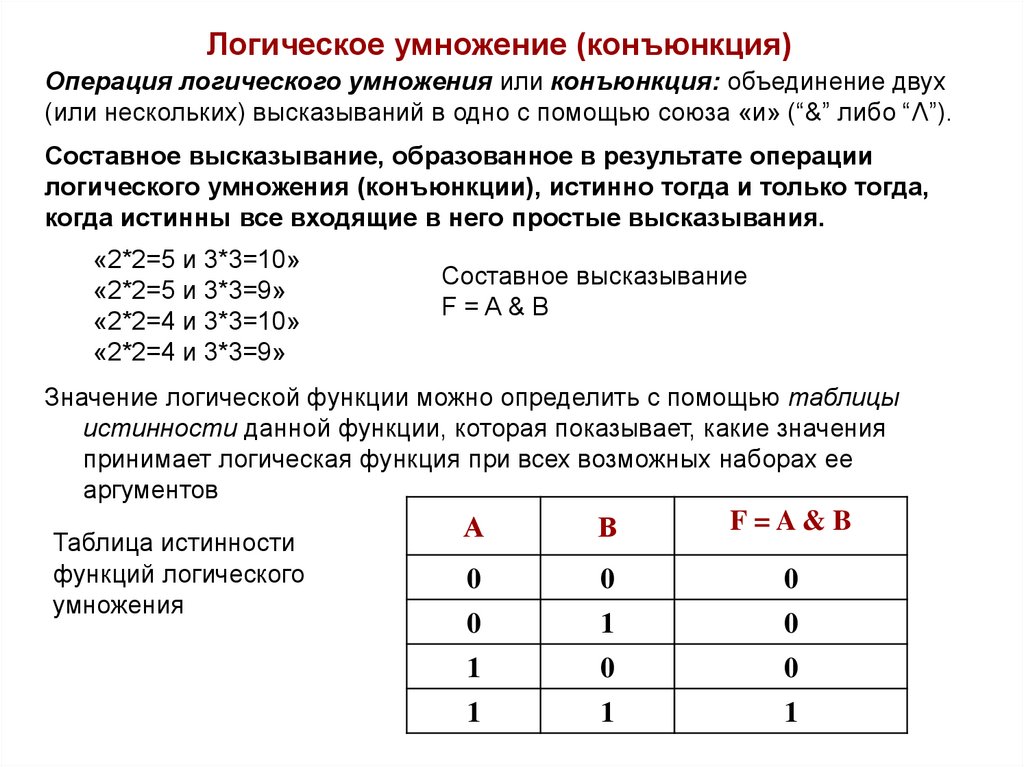
Логическое умножение (конъюнкция)
Операция логического умножения или конъюнкция: объединение двух
(или нескольких) высказываний в одно с помощью союза «и» (“&” либо “Λ”).
Составное высказывание, образованное в результате операции
логического умножения (конъюнкции), истинно тогда и только тогда,
когда истинны все входящие в него простые высказывания.
«2*2=5 и 3*3=10»
«2*2=5 и 3*3=9»
«2*2=4 и 3*3=10»
«2*2=4 и 3*3=9»
Составное высказывание
F=A&B
Значение логической функции можно определить с помощью таблицы
истинности данной функции, которая показывает, какие значения
принимает логическая функция при всех возможных наборах ее
аргументов
Таблица истинности
функций логического
умножения
А
В
F=A&B
0
0
0
0
1
0
1
0
0
1
1
1

8.

Логическое сложение (дизъюнкция)
Операция логического сложения или дизъюнкция - объединение двух
(или нескольких) высказываний с помощью союза «или» («v» либо «+»).
Составное высказывание, образованное в результате логического
сложения (дизъюнкции), истинно тогда, когда истинно хотя бы одно из
входящих в него простых высказываний.
«2*2=5 или 3*3=10»
«2*2=5 или 3*3=9»
«2*2=4 или 3*3=10»
«2*2=4 или 3*3=9»
Таблица истинности функции
логического сложения
Составное высказывание F = A v В
А
В
F=AvВ
0
0
0
0
1
1
1
0
1
1
1
1

9.

Логическое отрицание (инверсия)
Присоединение частицы «не» к высказыванию называется операцией
логического отрицания или инверсией (- над переменной).
Логическое отрицание (инверсия) делает истинное высказывание
ложным и, наоборот, ложное — истинным (Ā, ¬А)
F=Ā
А — «Два умножить на два равно четырем» — истина
F — «Два умножить на два не равно четырем» — ложь
Таблица истинности
функции логического
отрицания
А
F=Ā
0
1
1
0

10.

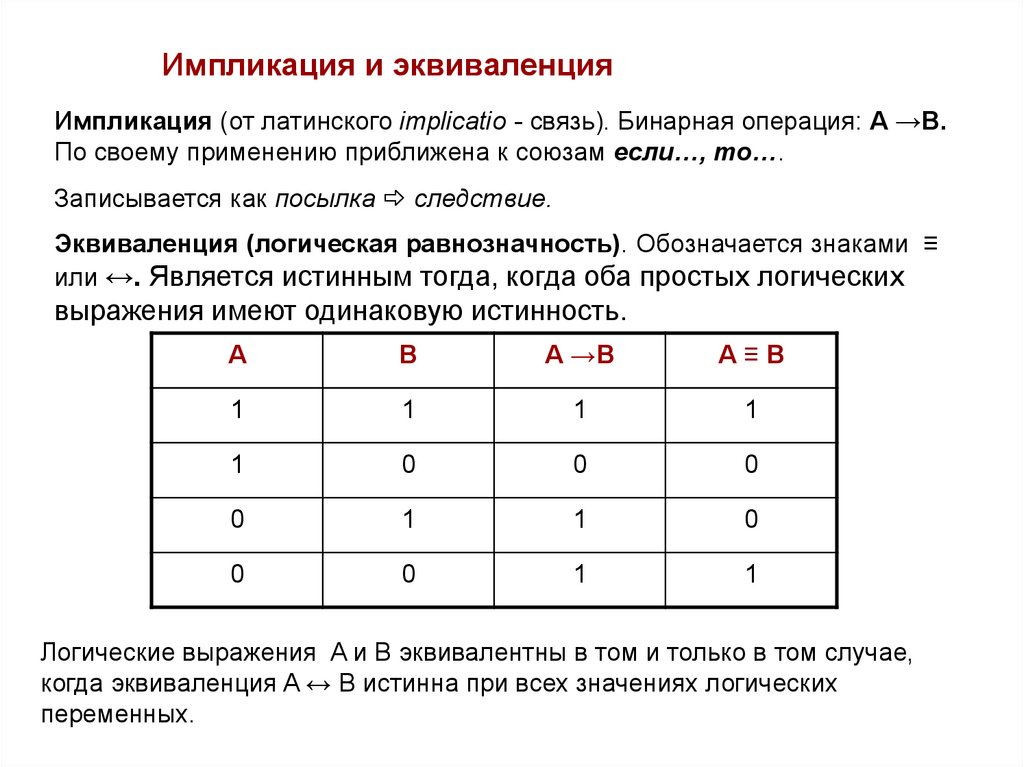
Импликация и эквиваленция
Импликация (от латинского implicatio - связь). Бинарная операция: А →В.
По своему применению приближена к союзам если…, то….
Записывается как посылка следствие.
Эквиваленция (логическая равнозначность). Обозначается знаками ≡
или ↔. Является истинным тогда, когда оба простых логических
выражения имеют одинаковую истинность.
А
В
А →В
А≡В
1
1
1
1
1
0
0
0
0
1
1
0
0
0
1
1
Логические выражения A и B эквивалентны в том и только в том случае,
когда эквиваленция A ↔ B истинна при всех значениях логических
переменных.

11.

Логические выражения и таблицы истинности
Логические выражения = логические переменные (высказывания) + знаки
логических операций (логические функции).
Составное высказывание «(2*2 = 5 или 2*2 = 4) и (2*2 ≠ 5 или 2*2 ≠ 4)»
А = «2*2 = 5» — ложно (0)
В = «2*2 = 4» — истинно (1)
Составное высказывание: (А v В) ∩ (А v В)
Последовательность выполнения логических операций:
1. инверсия
4. импликация
2. конъюнкция
3. дизъюнкция
5. эквивалентность
Для изменения указанного порядка могут использоваться скобки:
F = (A v B)&(Ā v В)
Истинность или ложность составных высказываний определяется формально,
руководствуясь законами алгебры высказываний, не обращаясь к смысловому
содержанию высказываний.
F = (A v B)&( Ā v В) = (0 v 1)&(1 v 0) = 1 & 1 = 1

12.

Алгоритм построения таблицы истинности
Последовательность действий при построении таблиц истинности:
1. количество строк равно количеству возможных комбинаций значений
логических переменных, входящих в логическое выражение. Если количество
логических переменных равно n, то количество строк — 2n.
2. количество столбцов равно количеству логических переменных плюс
количество логических операций.
3. построить макет таблицы с определённым количеством строк и столбцов,
обозначить столбцы и внести в таблицу возможные наборы значений исходных
логических переменных
4. заполнить таблицу по столбцам, выполняя базовые логические операции в
необходимой последовательности, просчитывая каждое действие
F = (A v B)&( Ā v В)

13.

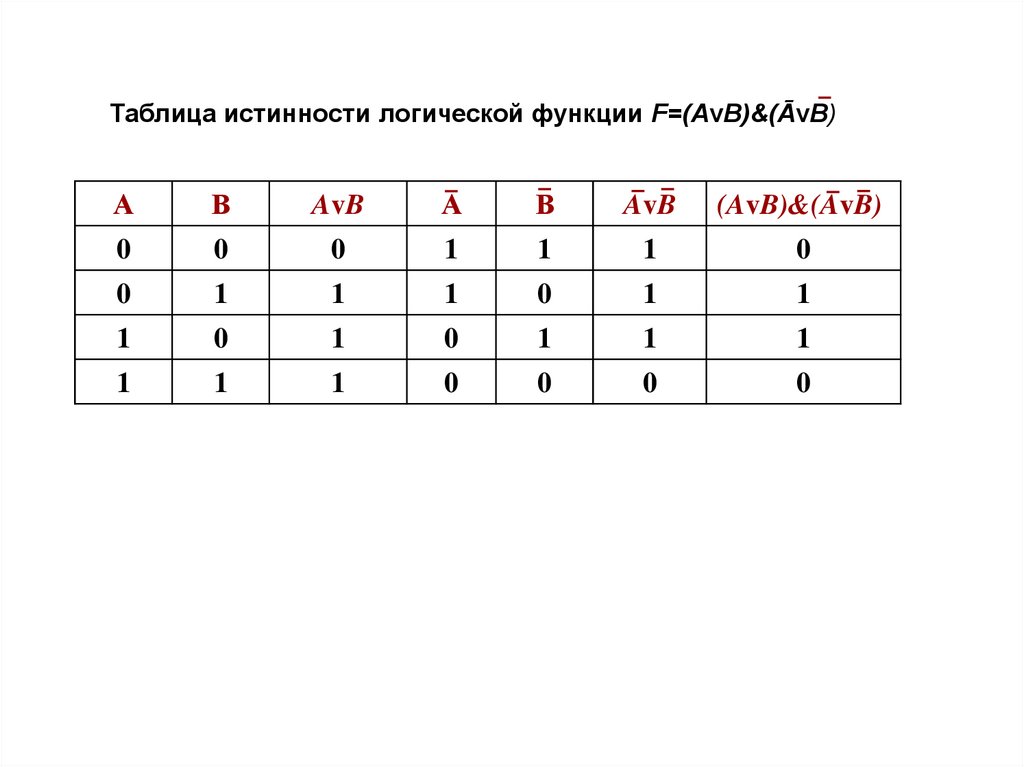
Таблица истинности логической функции F=(AvB)&(ĀvB)
А
В
AvB
А
В
AvB
(AvB)&(AvB)
0
0
0
1
1
1
0
0
1
1
1
0
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0

14.

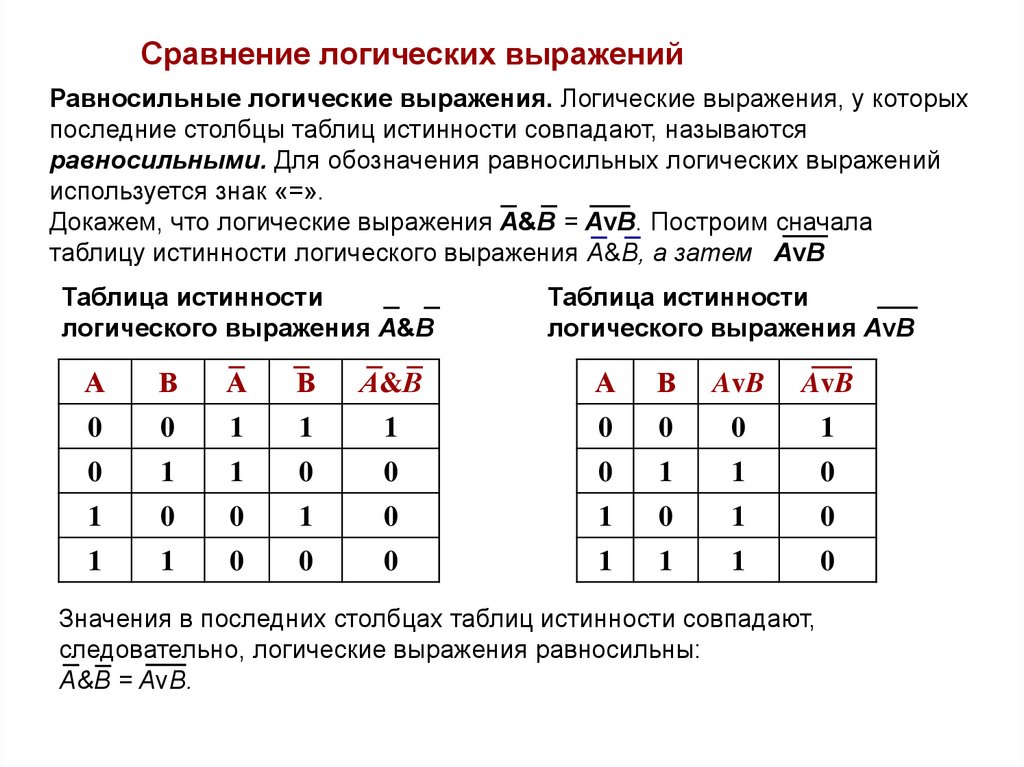
Сравнение логических выражений
Равносильные логические выражения. Логические выражения, у которых
последние столбцы таблиц истинности совпадают, называются
равносильными. Для обозначения равносильных логических выражений
используется знак «=».
Докажем, что логические выражения А&В = AvB. Построим сначала
таблицу истинности логического выражения А&В, а затем AvB
Таблица истинности
логического выражения А&В
Таблица истинности
логического выражения AvB
А
В
А
В
А&В
А
В
AvB
AvB
0
0
1
1
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
1
0
1
0
1
0
1
1
0
0
0
1
1
1
0
Значения в последних столбцах таблиц истинности совпадают,
следовательно, логические выражения равносильны:
А&В = AvB.

15.

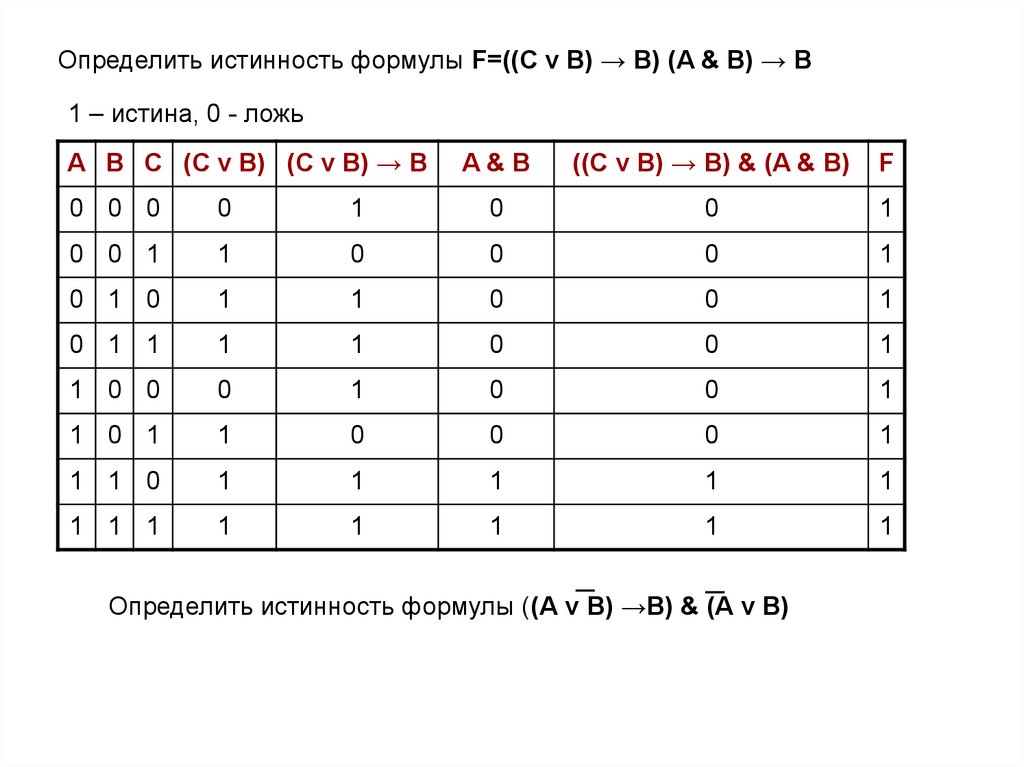
Определить истинность формулы F=((C v B) → B) (A & B) → B
1 – истина, 0 - ложь
А В С (C v B) (C v B) → B
A&B
((C v B) → B) & (A & B)
F
0 0 0
0
1
0
0
1
0 0 1
1
0
0
0
1
0 1 0
1
1
0
0
1
0 1 1
1
1
0
0
1
1 0 0
0
1
0
0
1
1 0 1
1
0
0
0
1
1 1 0
1
1
1
1
1
1 1 1
1
1
1
1
1
Определить истинность формулы ((А v В) →В) & (А v В)

16.

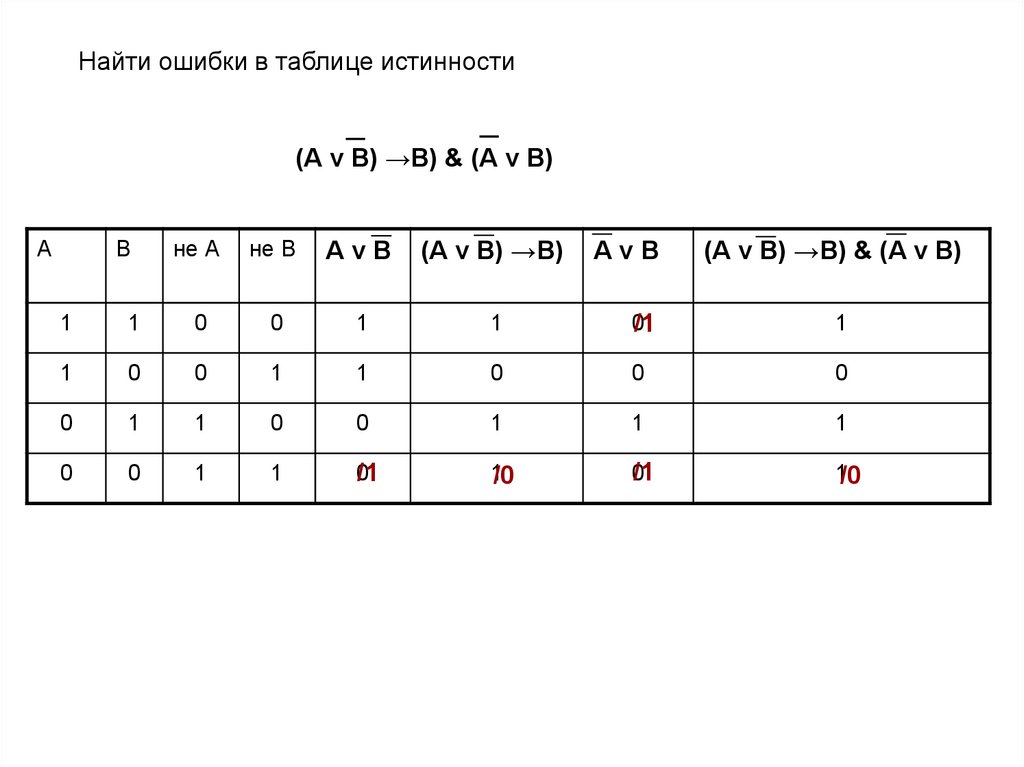
Найти ошибки в таблице истинности
(А v В) →В) & (А v В)
А
В
не А
не В
АvВ
(А v В) →В)
АvВ
(А v В) →В) & (А v В)
1
1
0
0
1
1
0/1
1
1
0
0
1
1
0
0
0
0
1
1
0
0
1
1
1
0
0
1
1
0
/1
1/0
/1
0
1/0

17.

Логические законы
Закон тождества
А=А
Закон исключённого третьего (либо истина, либо ложь)
Закон двойного отрицания (отрицания отрицания)
Закон коммутативности
(переместительный):
Закон ассоциативности:
А&В = В&А
Аv А=1
=
А=А
АvВ=ВvА
(А&В)&С = А&(В&С)
(А v В) v С = В v (А v С)
Закон дистрибутивности (распределительный). В отличие от обычной
алгебры за скобки можно выносит и общие слагаемые:
Относительно сложения
(А&В) v (А&С) = А&(В v С)
Закон склеивания
Относительно умножения
(А v В) &(А v С) = А v(В & С)
А&B+A&B=A
Закон исключения констант
(A+B)&(A+B)=A
сложение
умножение
Аv1=1, Аv0=А
А&1=А, А&0=0

18.

Преобразования логических переменных
Недостаток табличного способа определения истинности: большое
количество логических переменных даёт большое количество вариантов.
Законы де Моргана
Законы поглощения
(A&B)=AvB
(AvB)=A&B
A&(AvB)=A
Av(A&B) =A
A&(AvB)=AВ
Av(A&B) =A
Закон равносильности AvA =A; A&А =A
Закон противоречия
А+А=1;
A&A =0
Формула имеет нормальную форму, если в ней отсутствуют знаки
эквивалентности, импликации, двойного отрицания, при этом знаки
отрицания находятся только при переменных.
A→B=AvB
A↔B= A&B v A&B = (AvB)&(AvB)

19.

Упростить логическое выражение:
1)
(А v В → В & С)
=
2)
=
((А v В) v (В & С)) =
((А v В) & (В & С)) =
(А v В) & В & С = В & С = 1
(А →А v В) v( В & (А & В)) = (А v (А v В)) v( В v (А & В)) =
(А v (А & В)) v( В v (А & В)) =
А v (А & В) v В v (А & В)
= А v 0 v В v 1= 1

20.

На вопрос, кто из трёх учащихся изучал логику, был получен ответ: Если
изучал первый, то изучал и второй, но неверно, что если изучал третий, то
изучал и второй. Кто изучал логику?
Введём переменные:
А - изучал первый;
В – изучал второй;
С – изучал третий.
Составляем сложное высказывание:
(А В) & (C B)
(А v В) & (C v B)
(А v В) & (C & B)
(А v В) & C & B
А&C&BvВ&C&B
Логику изучает третий ученик

21.

Задачи:
1) На выставке собак 1,2 и 3 места заняли собаки с кличками Джек, Лесси и
Гриф. Трое судей на вопрос хозяев собак ответили:
1-й судья: Джек занял второе место
2-й судья: Лесси заняла не второе место
3-й судья: Гриф не был первым
После объявления результатов оказалось, что двое судей ошиблись, а один
оказался прав. Как распределились призовые места?
Решение: Д2неЛ2неГ1
Д2Л2Г1 v Д2Л2Г1 v Д2Л2Г1 =
Д2Л2Г1 v Д2Л2Г1 v Д2Л2Г1 = 0 v 0 v 1
Ответ: Джек – 1, Лесси – 2, Гриф - 3

22.

2) Ограбили ювелирный магазин. Перед судом предстали трое известных
преступников: Трус, Балбес и Бывалый. Следствием установлено:
- если Трус не виновен или Балбес виновен, то Бывалый виновен;
- если Трус не виновен, то Балбес не виновен
Виновен ли Трус?
Решение: Тр – виновен, Бал – виновен, Быв - виновен
((Тр v Бал) Быв) & ( Тр Бал)
((Тр v Бал) v Быв) & ( Тр v Бал)
((Тр & Бал) v Быв) & ( Тр v Бал)
(Тр & Бал v Быв) & ( Тр v Бал)
(Тр v Быв) & (Бал v Быв) & ( Тр v Бал)
Трус виновен

23.

3) В лесу проводился кросс. Обсуждая его итоги, одна белка сказала:
«Заяц занял первое место, а второе – лиса». Вторая белка возразила:
«Заяц занял второе место, косуля – первое». На что филин заметил, что
в высказывании каждой белки одна часть верная, а другая – нет. Как
распределились места в кроссе?
Решение: Б1=З1Л2; Б2=З2К1
(З1Л2 v З1Л2) & (З2К1v З2К1)=1
З1Л2З2К1 v З1Л2З2К1 v З1Л2З2К1 v З1Л2З2К1=1
0v0v1v0=1

24.

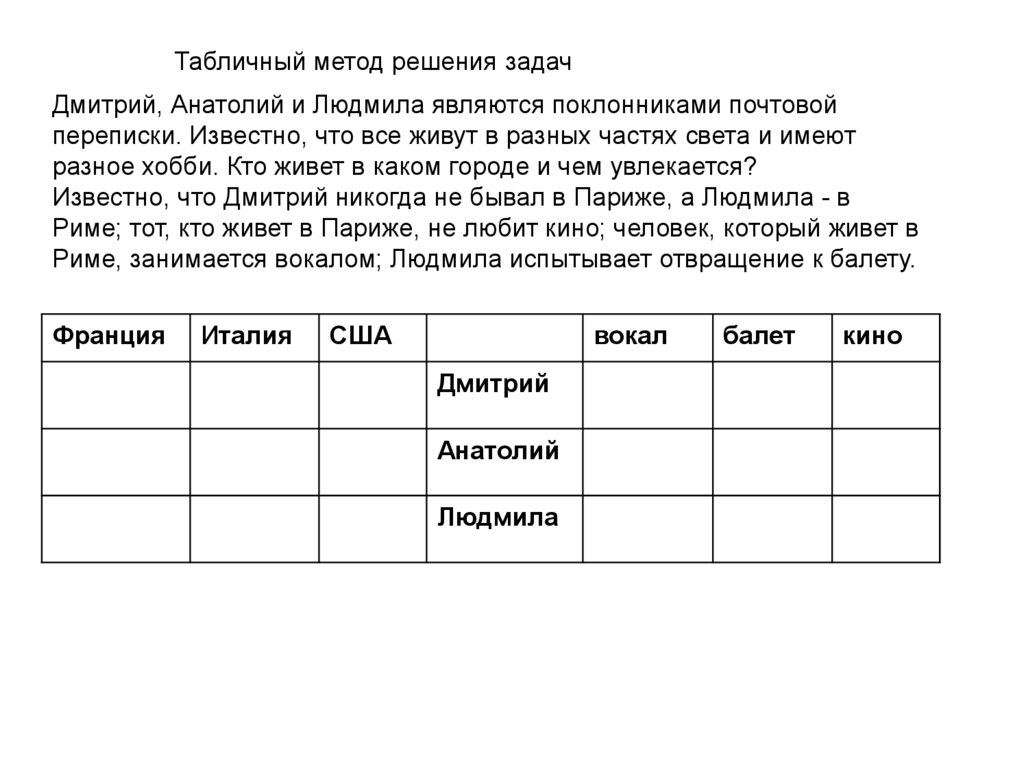
Табличный метод решения задач
Дмитрий, Анатолий и Людмила являются поклонниками почтовой
переписки. Известно, что все живут в разных частях света и имеют
разное хобби. Кто живет в каком городе и чем увлекается?
Известно, что Дмитрий никогда не бывал в Париже, а Людмила - в
Риме; тот, кто живет в Париже, не любит кино; человек, который живет в
Риме, занимается вокалом; Людмила испытывает отвращение к балету.
Франция
Италия
США
вокал
Дмитрий
Анатолий
Людмила
балет
кино

25.

Упростить логическое выражение
1) (А & В → С) & (В→С &D)
(А v В → С) & (В v С &D)
((А v В) v С) & (В v С &D)
(А & В v С) & (В v С &D)
((А & В) v С) & (В v С &D)
((А & В) v С) & (В v С &D)
2) (А v В) &(D→(С v А)) & (D→(А&С)) &(DvА)
(А v В) &(D v (С v А)) & (D v (А&С)) &(D&А)
(А v В) &(D & (С v А)) & (D v (А&С)) & D&А
(А v В) & D & С & А & (D v А&С) & D&А
(А v В) & 1 & С & А & (D v А&С) & 0