Логические основы построения компьютера

1.

2.

История развития алгебры логики
Джорж Буль
2 .11.1815г. -8.12.1864 г.
В 1842 году английский математик Джорж Буль
разработал математическую логику или алгебру логики,
которую впоследствии стали называть «булевой
алгеброй». В булевой алгебре высказывания принято
обозначать прописными латинскими Буквами: А,В,X,Y. В
алгебре Буля введены три основные логические
операции с высказываниями: сложение, умножение,
отрицание. Определены аксиомы (законы) алгебры
логики для выполнения этих операций. Действия,
которые
производятся
над
высказываниями,
записываются
в
виде
логических
выражений
Спустя 100 лет алгебра логики стала основой теории
цифровых вычислительных машин, ее используют в
компьютерной логике, электронике, в основе всех
микропроцессорных операций.

3.

«LOGOS» -- СЛОВО, МЫСЛЬ,
ПОНЯТИЕ, РАССУЖДЕНИЕ, ЗАКОН
ЛОГИКА -- ЭТО УЧЕНИЕ О СПОСОБАХ
РАССУЖДЕНИЙ И ДОКАЗАТЕЛЬСТВ,
НАУКА О ЗАКОНАХ И ФОРМАХ
МЫШЛЕНИЯ.

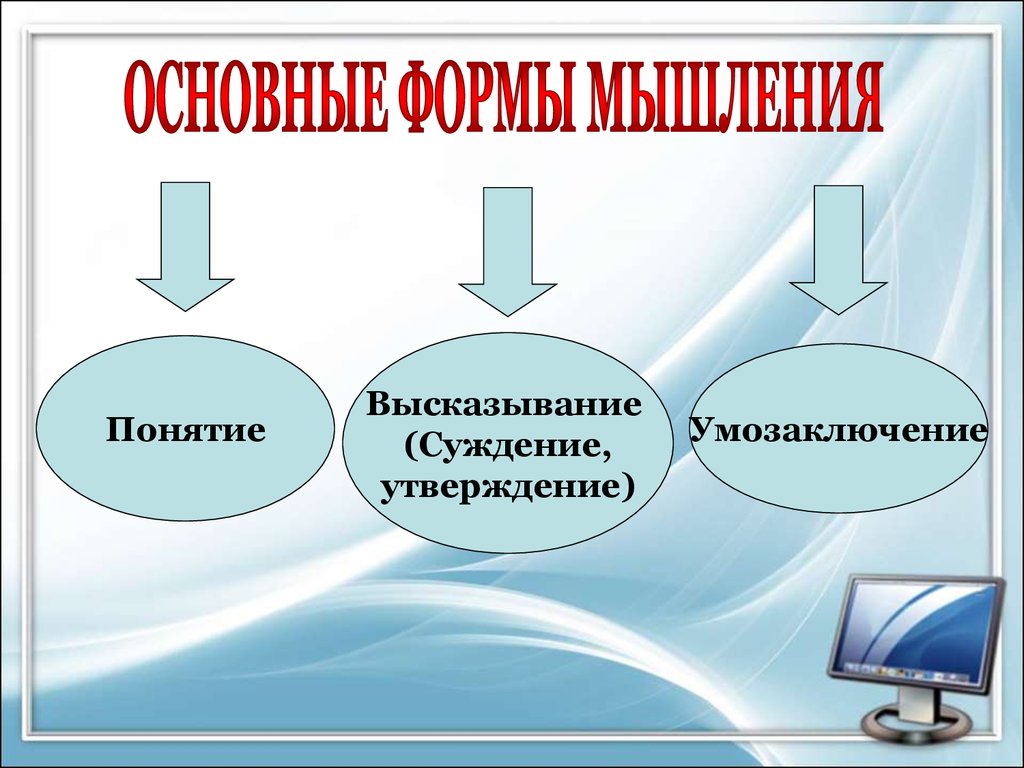
4.

Понятие
Высказывание
(Суждение,
утверждение)
Умозаключение

5.

Понятие – это форма мышления, фиксирующая
основные, существенные признаки объекта.
Например: компьютер, портфель, трапеция, ураганный ветер
Понятие
Содержание
Совокупность
существенных
признаков объекта
Например: содержание
понятия ПК –
универсальное
электронное устройство
для автоматической
обработки информации
Объем
Совокупность
предметов, на которую
распространяется
понятие
Например: понятие город – это
множество городов;
Понятие ПК – совокупность
существующих в мире ПК

6.

Высказывание – это форма мышления, в которой чтолибо утверждается или отрицается о свойствах реальных
предметов и отношениях между ними.
Высказывание является повествовательным предложением.
Высказывание
Истинное
Ложное
Вопросительные и восклицательные
предложения не являются высказываниями,
так как в них ни чего не утверждается и не
отрицается.

7.

Примеры высказываний
1
Все кошки серы
2
Париж – столица Франции
Ложь
Истина
3
Сумма углов треугольника -180 градусов
Истина
4
10+5=14
Ложь
5
Число 23 является простым
Истина
Выражения, не являющиеся высказываниями
1
Делайте утреннюю зарядку!
Не высказывание
2
На улице идет дождь ?
Не высказывание
3
5х - 2
Не высказывание
4
Разность чисел 12 и х равна 6.
Не высказывание

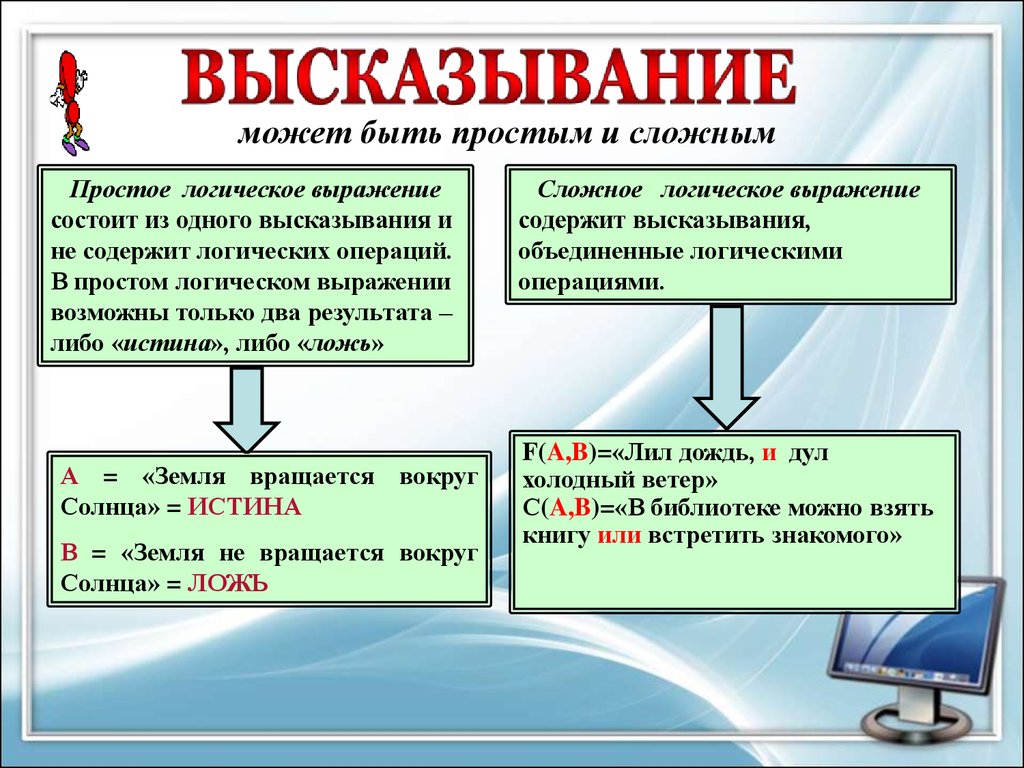
8.

может быть простым и сложным
Простое логическое выражение
состоит из одного высказывания и
не содержит логических операций.
В простом логическом выражении
возможны только два результата –
либо «истина», либо «ложь»
А = «Земля вращается вокруг
Солнца» = ИСТИНА
В = «Земля не вращается вокруг
Солнца» = ЛОЖЬ
Сложное логическое выражение
содержит высказывания,
объединенные логическими
операциями.
F(A,B)=«Лил дождь, и дул
холодный ветер»
С(A,B)=«В библиотеке можно взять
книгу или встретить знакомого»

9.

Умозаключение – это форма мышления, с помощью
которой из одного или нескольких суждений (посылок)
может быть получено новое суждение (заключение).
Посылками умозаключения – могут быть только
истинные суждения.
Например:
1. Все металлы – простые
вещества.
Литий – металл.
Литий – простое
вещество.
2. Все школьники –
отличники.
Вовочка – школьник.
Вовочка – отличник.

10.

Алгебра
высказываний

11.

Алгебра высказываний была разработана для того,
чтобы можно было определять истинность или ложность
составного высказывания, не вникая в их содержание.
Алгебра логики (алгебра высказываний) – раздел
математической логики, изучающий строение (форму,
структуру) сложных логических высказываний и способы
установления их истинности с помощью алгебраических
методов.
Под высказыванием (суждением) будем понимать
повествовательное предложение, относительно которого
можно сказать, истинно или ложно.

12.

Высказывание может принимать одно из двух
возможных логических значений:
ИСТИНА или ЛОЖЬ
ЛОГИЧЕСКИЕ
ПОСТОЯННЫЕ
Или
ЛОГИЧЕСКИЕ
КОНСТАНТЫ

13.

Простые высказывания в алгебре логики
обозначаются прописными латинскими
буквами.
А – «Два умножить на два равно четырем».
В – «Два умножить на два равно пяти».
Какова истинность высказываний?
Первое высказывание истинно (А = 1).
Второе высказывание ложно (В = 0).

14.

Составное высказывание на
естественном языке образуется с
помощью связок и, или, не,
которые в алгебре логики заменяются
на логические операции
умножения, сложения и отрицания.
Логические операции задаются
таблицами истинности.

15.

Логические операции
НЕ,
, not, ¬
И , , and, &, *, ·
ИЛИ, , or, +
=> ,
=, ~ , <=> , ≡ ,
Инверсия, логическое отрицание
Конъюнкция, логическое умножение
Дизъюнкция, логическое сложение
Импликация, логическое следование
Эквивалентность, логическое равенство

16.

Инверсия - логическое отрицание
Логическое отрицание делает истинное высказывание ложным и,
наоборот, ложное – истинным. От лат. inversio - переворачиваю
Таблица истинности функции логического отрицания
A
А
истина
ложь
ложь
истина
или
A
А
0
1
1
0
ИСТИНА – 1 ЛОЖЬ - 0
В переводе на естественный язык «Не А», «Неверно, что А»
Пример: Даны высказывания
А – «Число 4 – четное» = ИСТИНА
Не А – «Неверно, что число 4 – четное» = ЛОЖЬ

17.

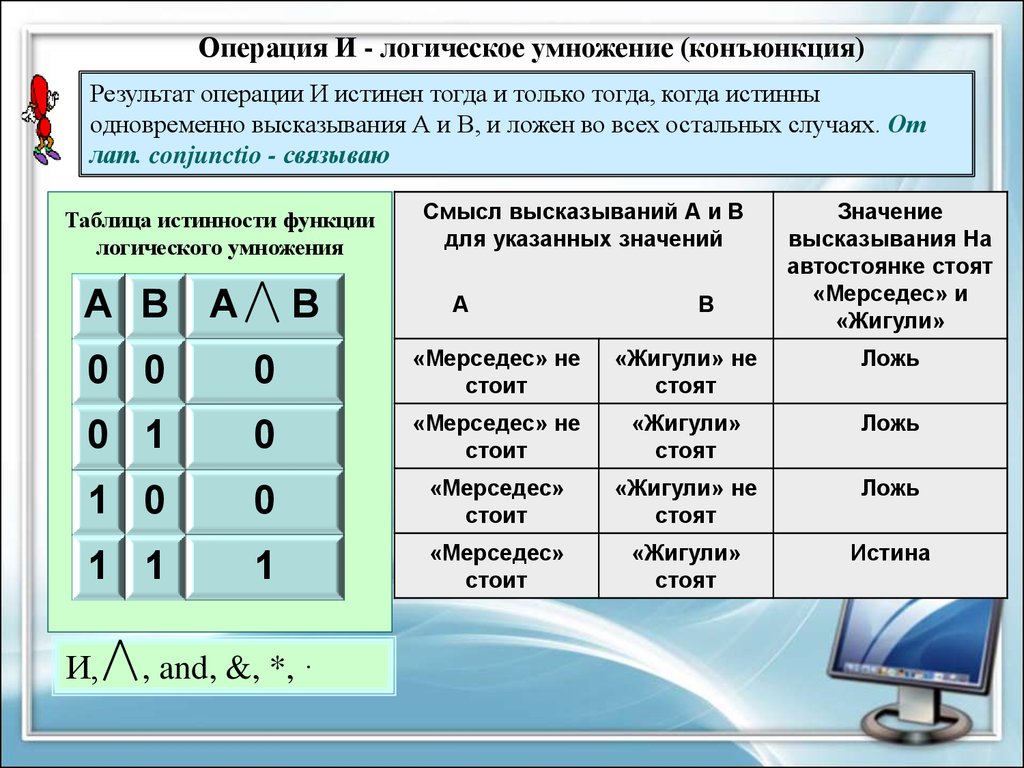
Операция И - логическое умножение (конъюнкция)
Результат операции И истинен тогда и только тогда, когда истинны
одновременно высказывания А и В, и ложен во всех остальных случаях. От
лат. conjunctio - связываю
Таблица истинности функции
логического умножения
A B A
B
Смысл высказываний А и В
для указанных значений
А
В
Значение
высказывания На
автостоянке стоят
«Мерседес» и
«Жигули»
0 0
0
«Мерседес» не
стоит
«Жигули» не
стоят
Ложь
0 1
0
«Мерседес» не
стоит
«Жигули»
стоят
Ложь
1 0
0
«Мерседес»
стоит
«Жигули» не
стоят
Ложь
1 1
1
«Мерседес»
стоит
«Жигули»
стоят
Истина
И,
, and, &, *, ·

18.

Операция ИЛИ - логическое сложение (дизъюнкция, объединение)
Результат операции ИЛИ истинен, когда истинно А, либо истинно В, либо
истинно и А и В одновременно, и ложно тогда, когда аргументы А и В –ложны
От лат. disjunctio – различаю.
Таблица истинности
функции логического
сложения
A
0
0
1
1
B
0
1
0
1
ИЛИ,
A
B
0
1
1
1
, or, +
Смысл высказываний А и В для
указанных значений
А
В
Значение
высказывания На
автостоянке стоят
«Мерседес» и
«Жигули»
«Мерседес» не
стоит
«Жигули» не
стоят
Ложь
«Мерседес» не
стоит
«Жигули»
стоят
Истина
«Мерседес» стоит
«Жигули» не
стоят
Истина
«Мерседес» стоит
«Жигули»
стоят
Истина

19.

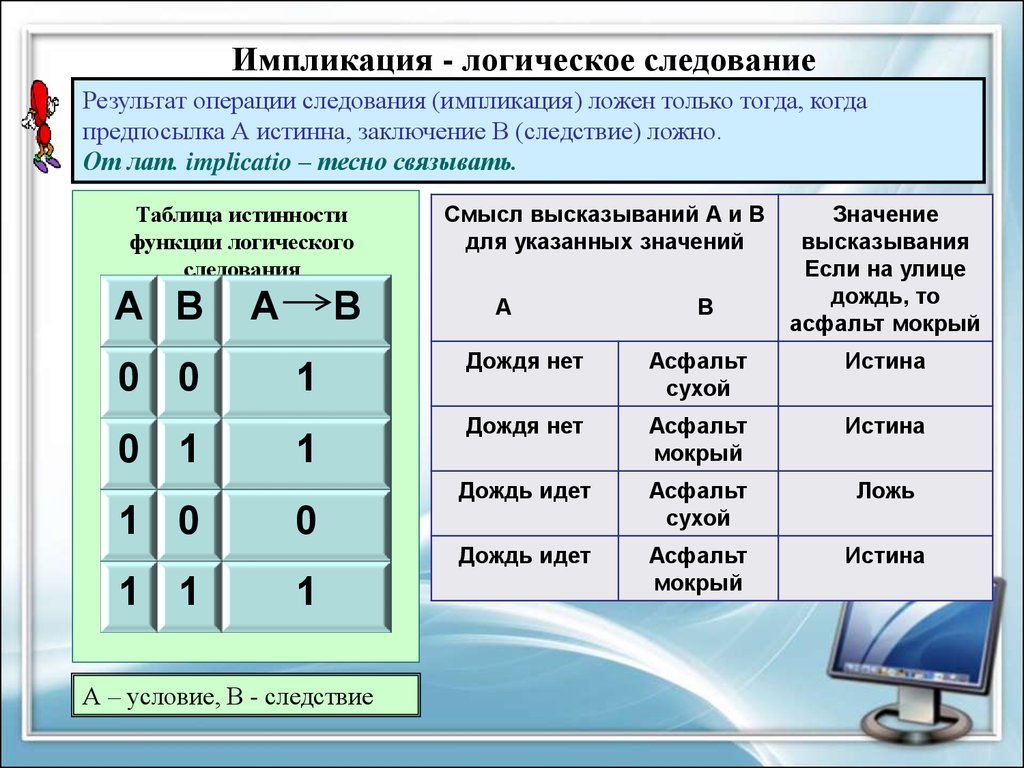
Импликация - логическое следование
Результат операции следования (импликация) ложен только тогда, когда
предпосылка А истинна, заключение В (следствие) ложно.
От лат. implicatio – тесно связывать.
Таблица истинности
функции логического
следования
A B
0 0
0 1
1 0
1 1
A
B
1
1
Смысл высказываний А и В
для указанных значений
А
Дождя нет
Асфальт
сухой
Истина
Дождя нет
Асфальт
мокрый
Истина
Дождь идет
Асфальт
сухой
Ложь
Дождь идет
Асфальт
мокрый
Истина
0
1
А – условие, В - следствие
В
Значение
высказывания
Если на улице
дождь, то
асфальт мокрый

20.

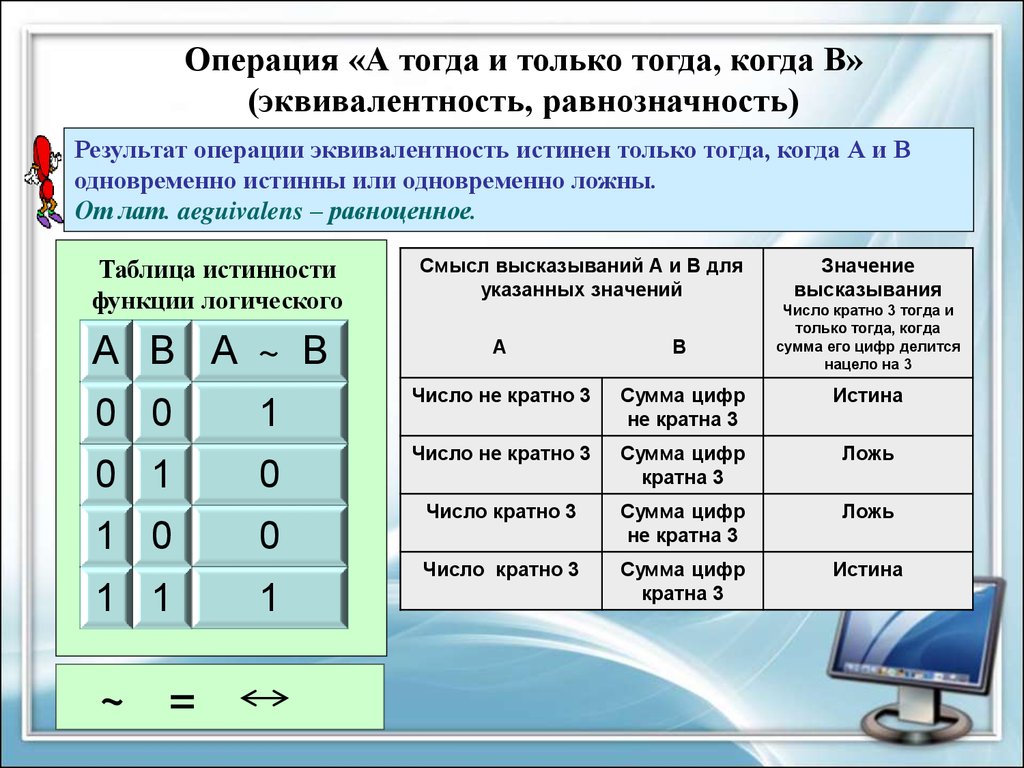
Операция «А тогда и только тогда, когда В»
(эквивалентность, равнозначность)
Результат операции эквивалентность истинен только тогда, когда А и В
одновременно истинны или одновременно ложны.
От лат. aeguivalens – равноценное.
Таблица истинности
функции логического
равенства
A B A ~ B
0 0
0 1
1 0
1 1
~ =
1
0
0
1
Смысл высказываний А и В для
указанных значений
Значение
высказывания
Число кратно 3 тогда и
только тогда, когда
сумма его цифр делится
нацело на 3
А
В
Число не кратно 3
Сумма цифр
не кратна 3
Истина
Число не кратно 3
Сумма цифр
кратна 3
Ложь
Число кратно 3
Сумма цифр
не кратна 3
Ложь
Число кратно 3
Сумма цифр
кратна 3
Истина

21.

Порядок выполнения логических
операций
1.
2.
3.
4.
5.
6.
Действия в скобках.
Операция отрицания (“не”).
Конъюнкция (“и”).
Дизъюнкция (“или”).
Импликация .
Эквивалентность
.

22.

Основные законы булевой алгебры
№
Закон
Пояснение
Для
дизъюнкции
Для
конъюнкции
1
Ассоциативность
Независимость от
порядка выполнения
однотипных
действий
А+(В+С)=
(А+В)+С=А+В
+С
А∙(В∙С)=
(А∙В) ∙С
=А∙В∙С
2
Коммутативност
ь
Независимость от
перестановки
А+В=В+А
А∙В=В∙А
3
Дистрибутивност
ь (распределение)
Правило раскрытия
скобок и внесение за
скобки
А+(В∙С)=
(А+В) ∙(А+С) =
(А+В) ∙(В+С) =
(А∙С)+В
(А+В)∙С=
А∙С+В∙С =
А∙В +В∙С =
В∙ (А+С)
4
Идемпотентность
Отсутствие степеней
и коэффициентов
А+А=А
А∙А=А
5
Инволюция
Двойная инверсия
А=А

23.

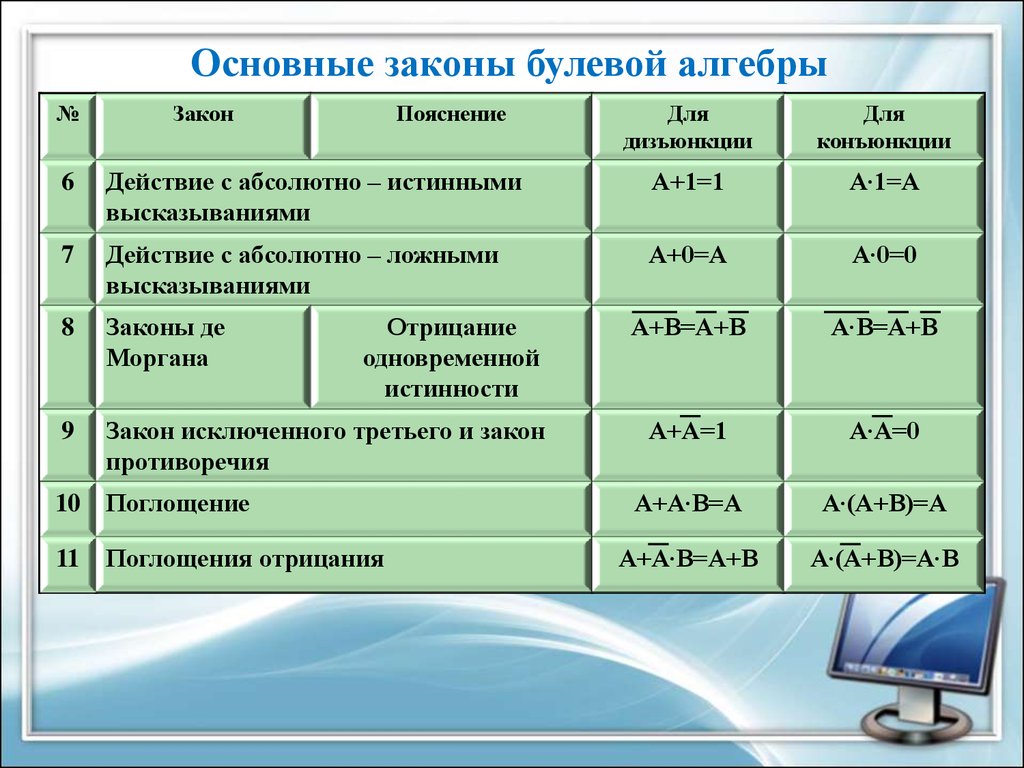
Основные законы булевой алгебры
№
Закон
Пояснение
Для
дизъюнкции
Для
конъюнкции
6
Действие с абсолютно – истинными
высказываниями
А+1=1
А∙1=А
7
Действие с абсолютно – ложными
высказываниями
А+0=А
А∙0=0
8
Законы де
Моргана
А+В=А+В
А∙В=А+В
9
Закон исключенного третьего и закон
противоречия
А+А=1
А∙А=0
А+А∙В=А
А∙(А+В)=А
А+А∙В=А+В
А∙(А+В)=А∙В
Отрицание
одновременной
истинности
10 Поглощение
11
Поглощения отрицания

24.

РЕШЕНИЕ
ЗАДАЧ

25.

Задача. Формулой логического высказывания:
«Если Катя окончит четверть без «троек» и каждый день
будет мыть посуду, то родители купят ей ноутбук»
является…
1) А => (В & С);
2) (А│В) &С;
3) (A&B) =>C;
4) (A=> B)&C.
ОТВЕТ: (A&B) =>C.

26.

Составление таблиц истинности по логической формуле
Дано логическое выражение А∙В. Требуется построить
таблицу истинности.
А
В
В
А∙В
0
0
1
0
0
1
0
0
1
0
1
1
1
1
0
0

27.

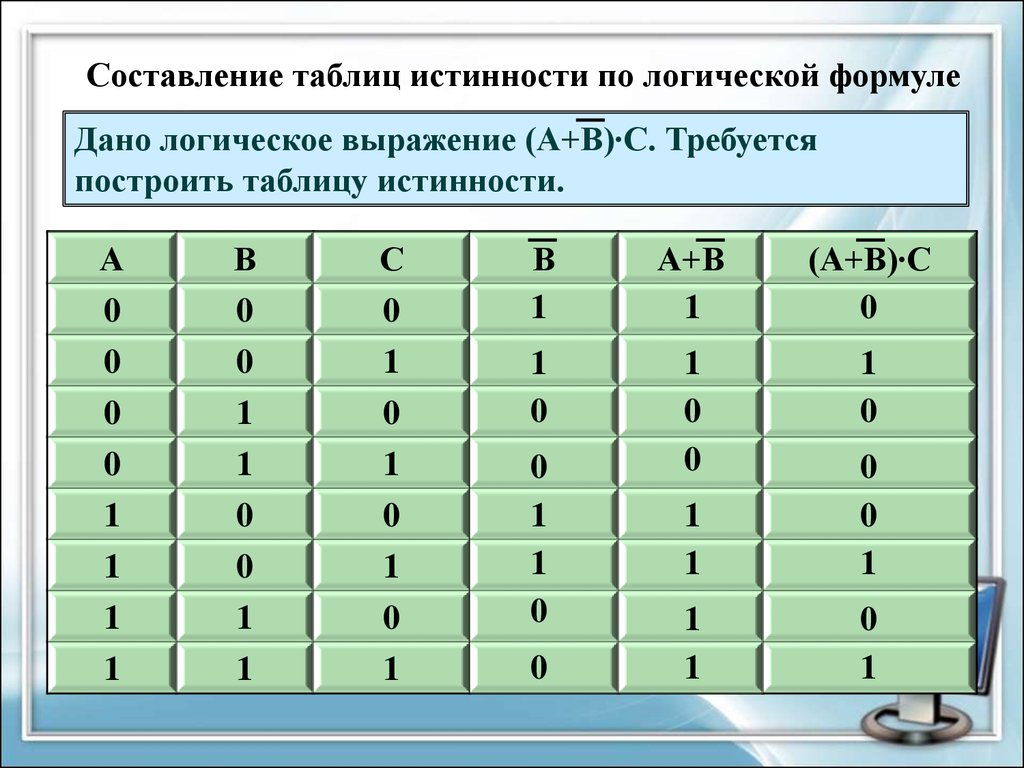
Составление таблиц истинности по логической формуле
Дано логическое выражение (А+В)∙С. Требуется
построить таблицу истинности.
А
0
0
В
0
0
С
0
1
0
0
1
1
1
0
0
1
0
1
0
1
1
1
1
1
0
1
В
1
А+В
1
(А+В)∙С
0
1
0
1
0
0
1
0
0
1
1
0
0
1
1
0
0
1
1
1
0
1

28.

Задача.
" Кто преступник"
Определить участника преступления, исходя из двух
посылок:
1) "Если Иванов не участвовал или Петров участвовал, то
Сидоров участвовал";
2) "Если Иванов не участвовал, то Сидоров не участвовал".
Решение
Составим выражения:
I - "Иванов участвовал в преступлении";
P - "Петров участвовал в преступлении";
S - "Сидоров участвовал в преступлении".
Запишем посылки в виде формул:
¬I˅P→S и ¬I→¬S

29.

Составим таблицу
Из таблицы видно, что совершил преступление
Иванов.

30.

Применим для решения этой же задачи
преобразования с помощью законов алгебры
логики:
Тогда имеем:
F(I,P,S)=( ¬I˅P→S) &( ¬I→¬S)=(¬(¬I˅P)˅S) & (I˅¬S) =
= (I & ¬P ˅S) & (I ˅¬S) = I&¬P˅ I & S˅ I &¬P &¬S ˅0 =
= I&¬P ˅ I & S = I & (¬P˅S)
Из последнего выражения видно, что выражение
верно, если I=1, значит преступник - Иванов.