Застосування похідної для дослідження функції

1.

ТЕМА. Застосування похідної для дослідження функції
Схема дослідження функції f(x):
1) знайти область визначення функції;
2) дослідити функцію на парність/непарність та
періодичність (для тригонометричних функцій);
3) знайти точки перетину графіка функції з осями
координат (якщо це можливо);
4) знайти похідну функції та її критичні точки;
5) знайти проміжки зростання/спадання та екстремуми
функції;
6) побудувати графік функції.

2.

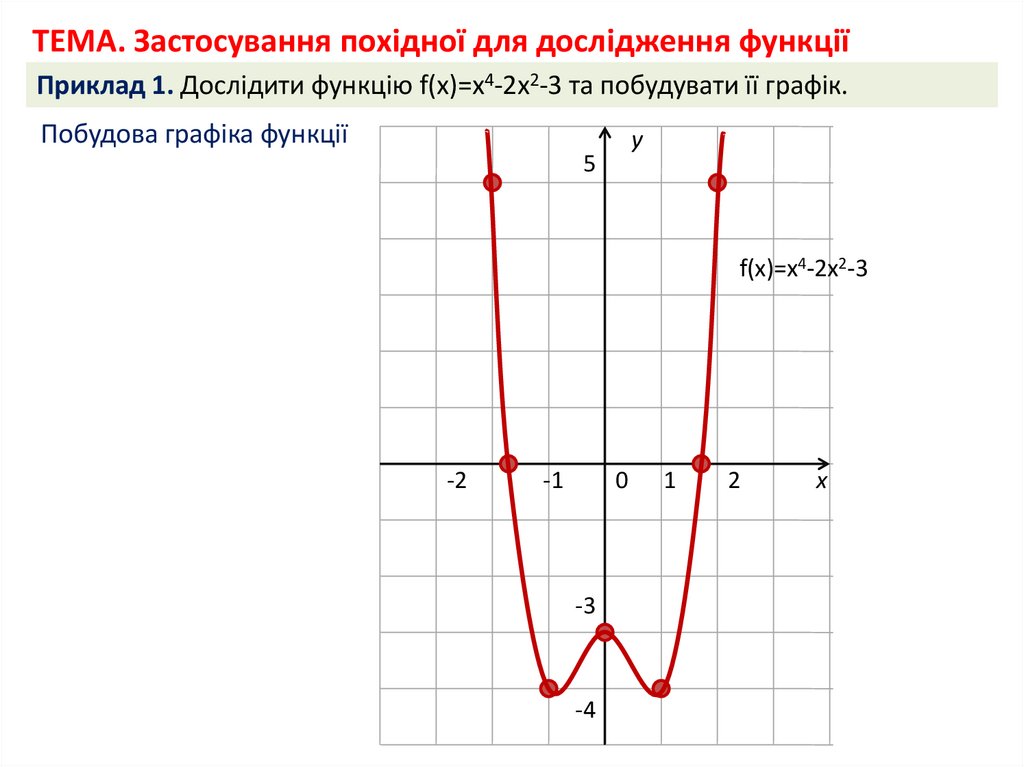
ТЕМА. Застосування похідної для дослідження функції
Приклад 1. Дослідити функцію f(x)=х4-2х2-3 та побудувати її графік.
D(f)=R;
f(-x)= (-х)4-2(-х)2-3= х4-2х2-3=f(x); - функція парна,
тому її графік симетричний відносно осі Оу.
Точки перетину з осями координат:
з віссю Оу х=0; f(0)=-3;
з віссю Ох у=0; х4-2х2-3=0;
f’(x)= 4х3-4х;
f’(x)= 0;
-
x 3 1.7
4х3-4х=0; 4х(х2-1)=0;
х=-1, x=1, х=0 – критичні точки;
min
-1
+
max
min
–
0
f(-1)=f(1)= 1-2-3=-4;
1
+
х

3.

ТЕМА. Застосування похідної для дослідження функції
Приклад 1. Дослідити функцію f(x)=х4-2х2-3 та побудувати її графік.
Побудова графіка функції
y
5
f(x)=х4-2х2-3
-2
-1
0
-3
-4
1
2
x

4.

ТЕМА. Застосування похідної для дослідження функції
Приклад 2. Дослідити функцію y x 3x та побудувати її графік.
2
x 1
D(у): х+1≠0; х≠-1; - область визначення на симетрична відносно початку
координат, тоді функція ні парна, ні непарна.
Точки перетину з осями координат:
з віссю Оу х=0; у(0)=0; (0;0)
з віссю Ох у=0; x 2 3x
0; х2-3х=0; х=0;х=3; х≠-1; (3;0)
x 1
(2 x 3)( x 1) ( x 2 3x) x 2 2 x 3
y
( x 1) 2
( x 1) 2
у’= 0;
+
х2+2х+3=0;
х=1, x=3 – критичні точки;
max
min
-
-3
у(-3)=-9;
-1
1
у(1)=-1;
+
х

5.

ТЕМА. Застосування похідної для дослідження функції
Приклад 1. Дослідити функцію y x 3x та побудувати її графік.
2
x 1
Побудова графіка функції

6.

ТЕМА. Застосування похідної для дослідження функції
Приклад 3. Дослідити функцію f ( x) x 4 та побудувати її графік.
x2
D(f): х≠0;
f ( x) x
4
4
x
( x) 2
x2
- функція ні парна, ні непарна.
Точки перетину з осями координат:
графік не перетинає вісь Оу (х ≠0);
4
з віссю Ох f(x)=0; x 2 0; х3=-4; x 3 4 1.6
x
8
f ( x) 1 3
x
f’(x)= 0;
1
8
3=8; х≠0
х
0
;
x3
х=2 – критична точка;
+
0
min
+
2
f(2)=3;
х

7.

ТЕМА. Застосування похідної для дослідження функції
Приклад 3. Дослідити функцію f ( x) x 4
2
та побудувати її графік.
x
y
Побудова графіка функції
f ( x) x
3
1
3 4
-2
-1
0
2
x
4
x2

8.

Список використаної літератури:
Математика. Підручник. 10 клас (рівень стандарту). Авт. Істер О. С.
Математика. Підручник. 10 клас (рівень стандарту). Авт. Нелін Є. П.
Математика. Підручник. 10 клас (рівень стандарту). Авт. Мерзляк А. Г.
Математика. Підручник. 10 клас (рівень стандарту). Авт. Бевз Г. П.