Similar presentations:
Похідна функції, її геометричний та фізичний зміст
1.
2.
1. Приріст функції та приріст аргументуЗафіксуємо точку х0 з області визначення функції у = f(х).
Нехай х — довільна точка з деякого околу точки х0
Тоді Δ x = x – x0 - приріст аргументу
Звідси
x = x0 + Δ x
Різниця х — х0 називається приростом
незалежної змінної
(або аргументу) у точці x0 і позначається Δx
(чит. Дельта ікс)
Δf (x0 ) = f ( x)
f ( x0 )
– приріст функції в точці х0, або
Δf (x0 ) = f ( x0 + Δx)
f ( x0 )
3.
Похіднаy
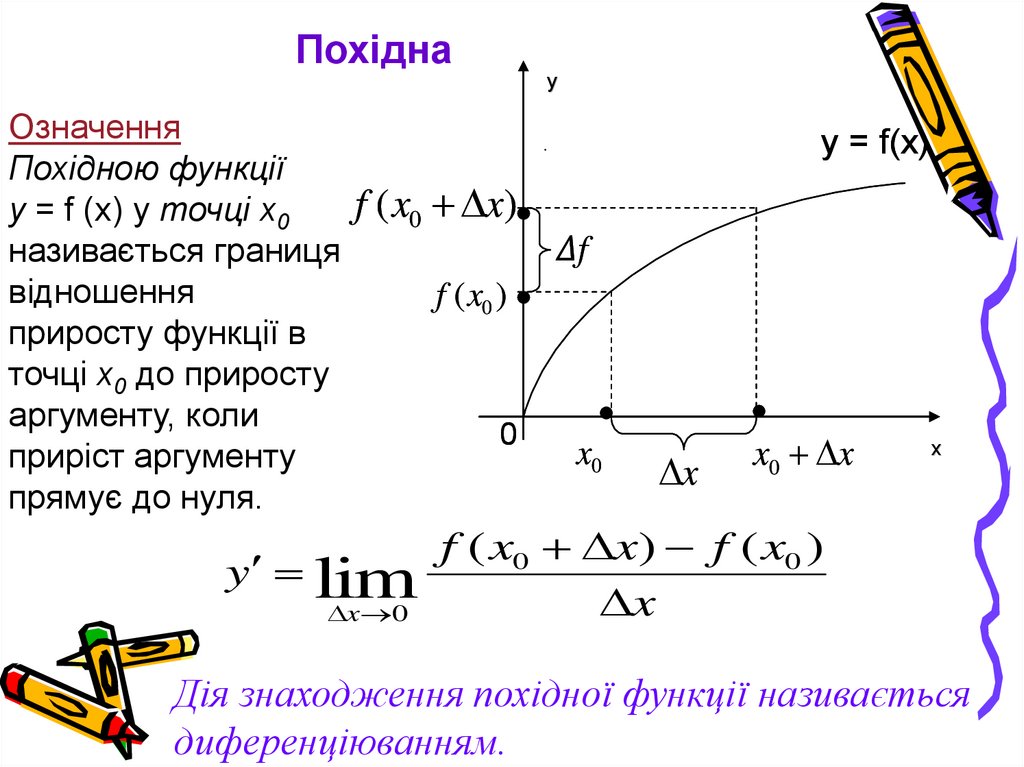
Означення
Похідною функції
f ( x0 x)
у = f (x) у точці х0
називається границя
відношення
f ( x0 )
приросту функції в
точці х0 до приросту
аргументу, коли
0
приріст аргументу
прямує до нуля.
y lim
x 0
у = f(х)
Δf
x0
x
x0 x
x
f ( x0 x) f ( x0 )
x
Дія знаходження похідної функції називається
диференціюванням.
4.
Похідніелементарних
функцій.
C 0
x 1
n
n 1
x n x
1
x
2 x
1
n
x
n 1
n
n x
1
1
2
x
x
5.
6.
Розум полягає не тільки в знанні , а й в уміннізастосувати знання на ділі.
Зразки виконання завдань
Використовуємо ці три правила
1) у = х5
2) у = 2х3
3) у = -3х-4
4) у = х3 + 2х2 – 5х
5) у = 2х4 – 3х2 + 6х
у′ = 5х4
у′ = 6х2
у′ = 12х-5
у′ = 3х2 + 4х - 5
у′ = 8х3 - 6х + 6
Аристотель
7.
Геометричне значення похідноїЗначення похідної функції у = f(х) у точці х0 дорівнює
кутовому коефіцієнту дотичної до графіка функції у =
f(х) у точці х0:
k = f´(x0) = tg α,
де α – кут, який утворює дотична з додатним напрямом
осі абсцис
у = f´(x0) • (x – x0) + f(x0) –
рівняння дотичної до графіка
функції у = f(х) у точці х0
f(х0)
α


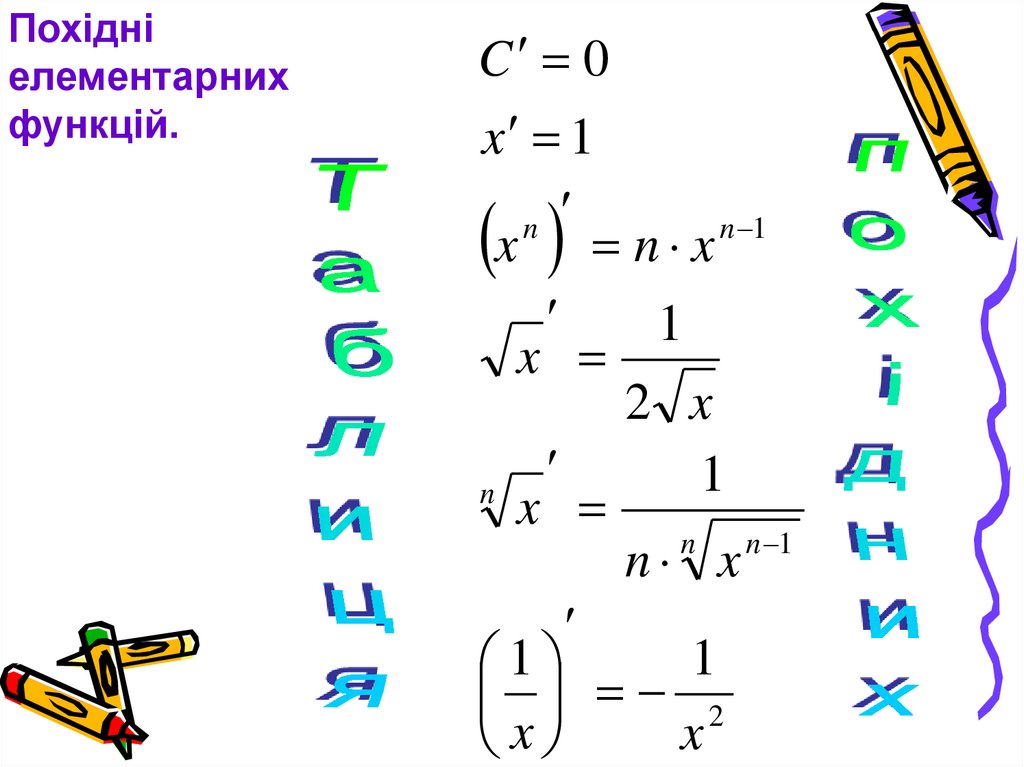




 mathematics
mathematics








