Вычисление площади фигуры. Урок 2

1. Вычисление площади фигуры.

* Вычисление
площади фигуры.
Геометрическая интерпретация интеграла
Урок 2.

2.

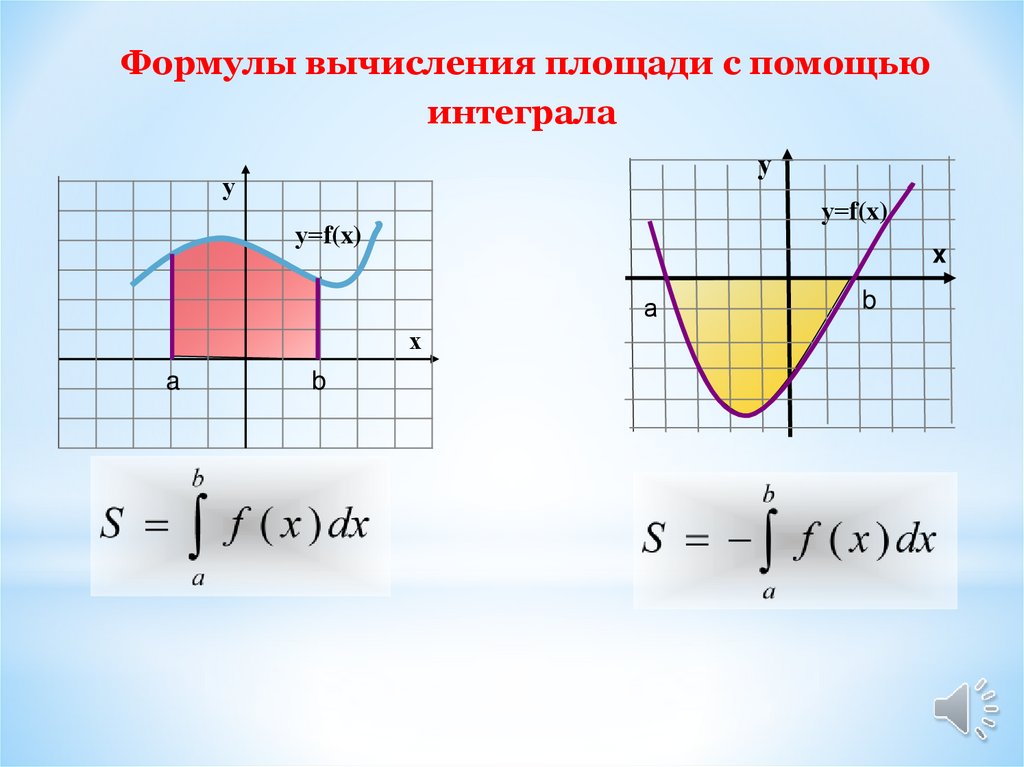
Формулы вычисления площади с помощью
интеграла
у
у
у=f(x)
у=f(x)
x
а
х
a
b
b

3.

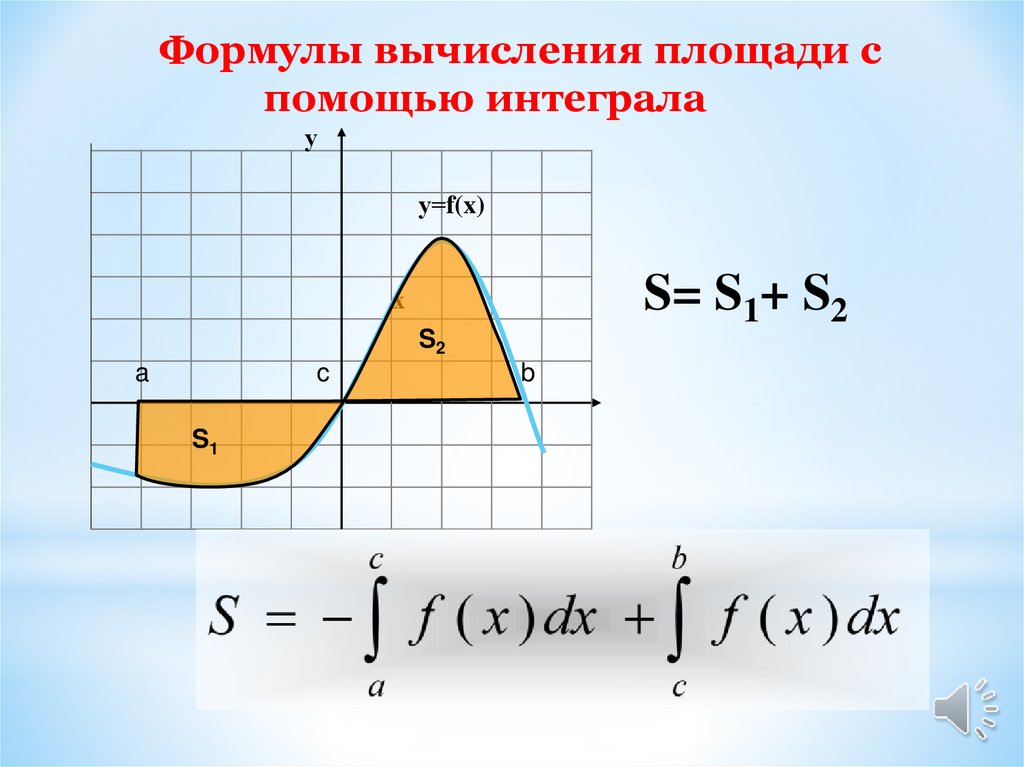
Формулы вычисления площади с
помощью интеграла
у
у=f(x)
S= S1+ S2
х
S2
a
c
S1
b

4.

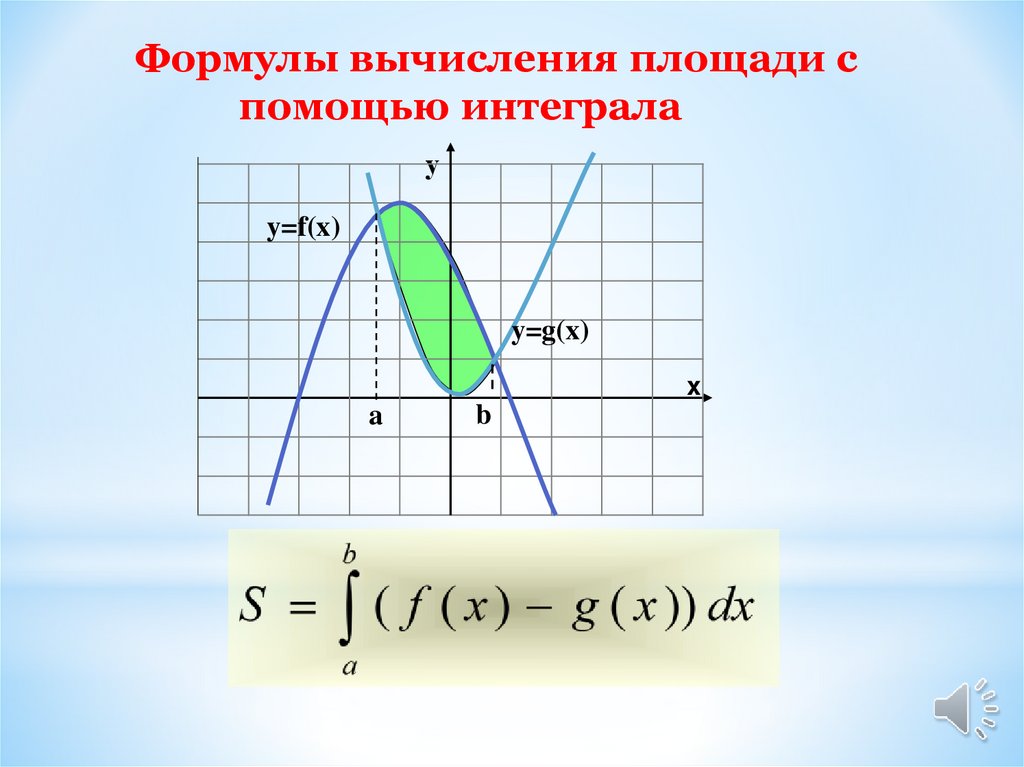
Формулы вычисления площади с
помощью интеграла
у
y=f(x)
y=g(x)
x
a
b

5.

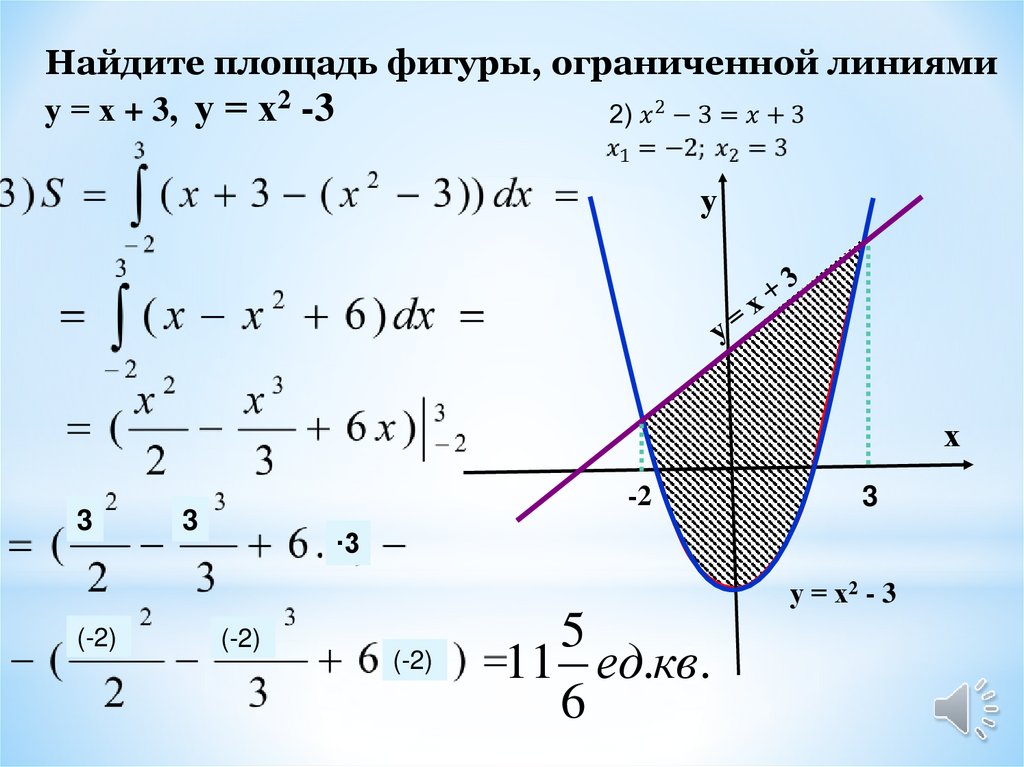
Найдите площадь фигуры, ограниченной линиями
у = х + 3, у = х2 -3
у
х
3
-2
3
3
∙3
у = х2 - 3
(-2)
(-2)
(-2)
5
11 ед.кв.
6

6.

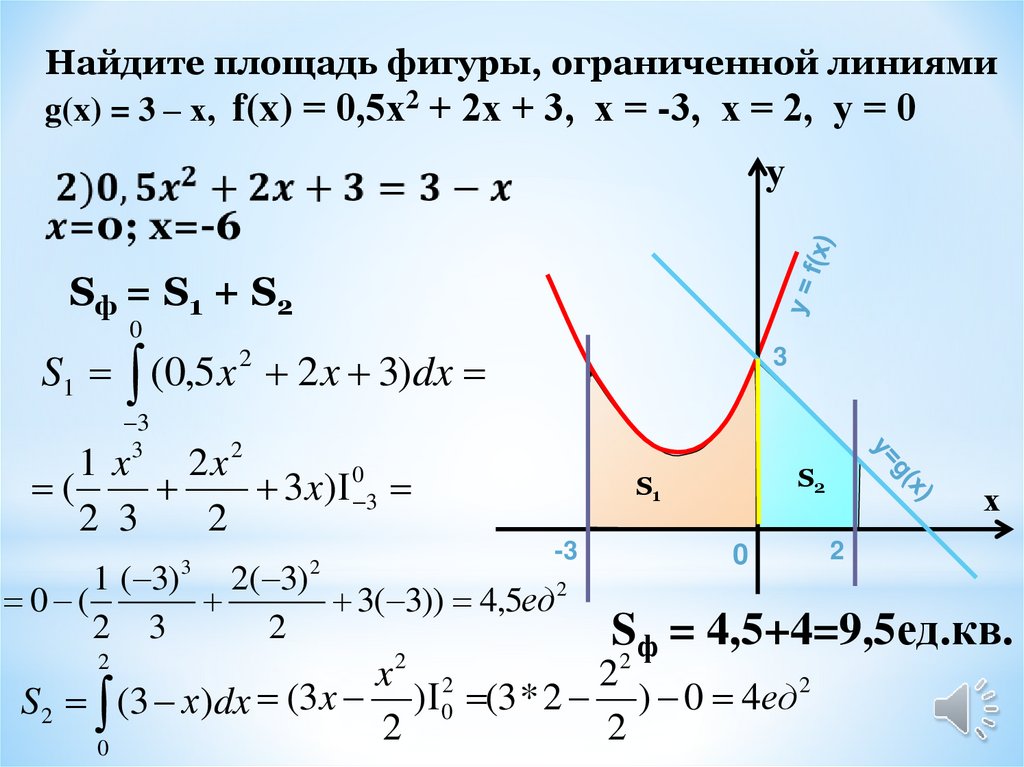
Найдите площадь фигуры, ограниченной линиями
g(x) = 3 – х, f(x) = 0,5х2 + 2х + 3, х = -3, х = 2, у = 0
у
Sф = S1 + S2
0
S1 (0,5 x 2 2 x 3)dx
3
3
1 x3 2 x 2
(
3x) 0 3
2 3
2
-3
1 ( 3) 2( 3)
0 (
3( 3)) 4,5ед 2
2 3
2
3
2
S2
S1
0
2
Sф = 4,5+4=9,5ед.кв.
x2 2
22
2
(
3
x
)
(
3
*
2
)
0
4
ед
S 2 (3 х)dx
0
2
2
0
2
х

7.

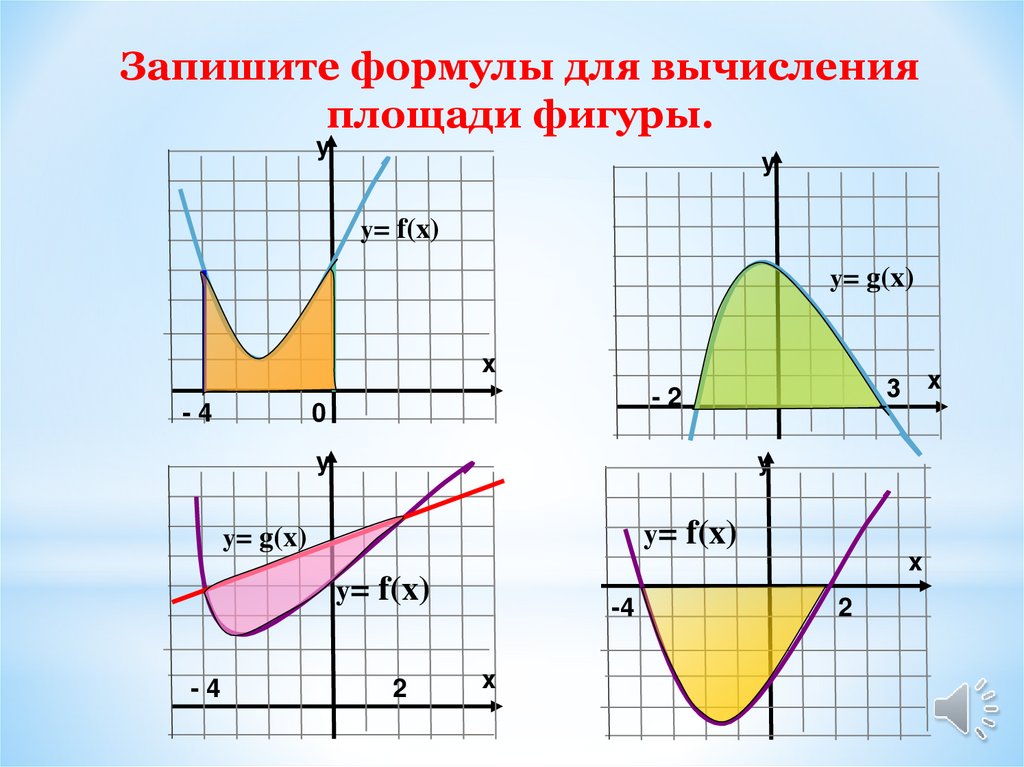
Запишите формулы для вычисления
площади фигуры.
y
y
y= f(x)
y= g(x)
x
-4
0
y
y
y= f(x)
y= g(x)
x
y= f(x)
-4
x
-2
2
-4
x
2

8.

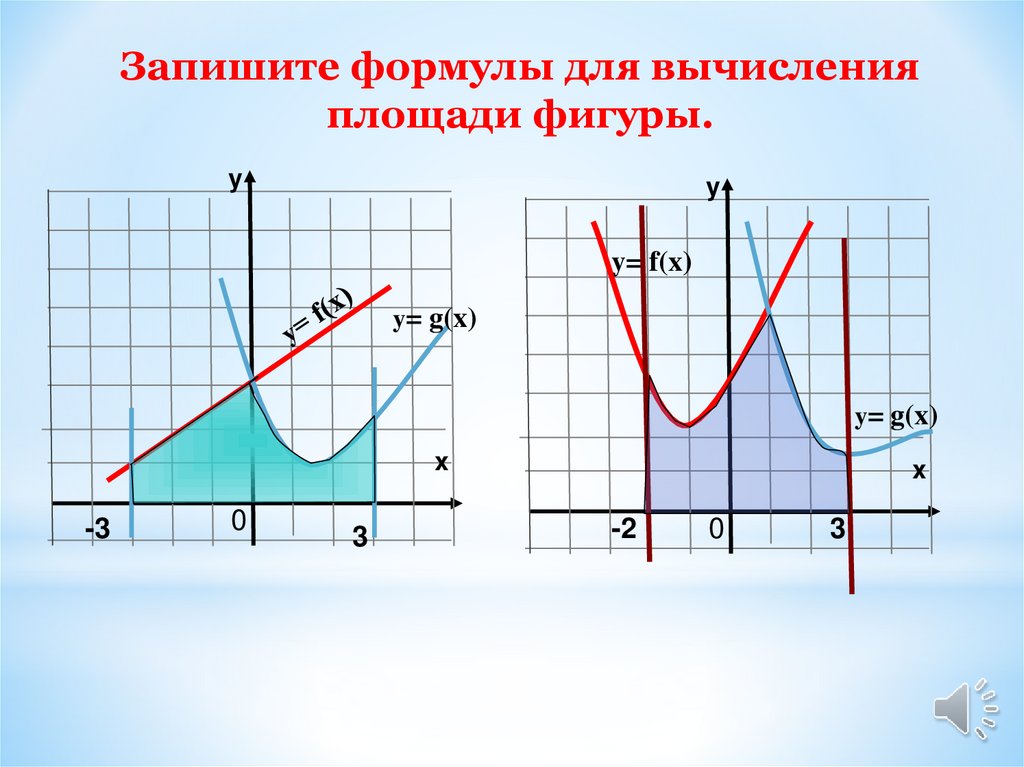
Запишите формулы для вычисления
площади фигуры.
y
y
y= f(x)
y= g(x)
y= g(x)
x
-3
0
3
x
-2
0
3