Similar presentations:
Задание точки, прямой, плоскости и многогранников на комплексном эпюре (чертеже) Монжа (лекция № 04)
1.
ПЕНЗЕНСКИЙГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра прикладной информатики
ДИСЦИПЛИНА
ИНЖЕНЕРНАЯ И КОМПЬЮТЕРНАЯ ГРАФИКА
РАЗДЕЛ I. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Тема 1 раздела
ЗАДАНИЕ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ И МНОГОГРАННИКОВ
НА КОМПЛЕКСНОМ ЭПЮРЕ (ЧЕРТЕЖЕ) МОНЖА
Пенза 2017 г.
2.
ПЛАН ПРОВЕДЕНИЯ ЛЕКЦИИ № 4Дисциплина
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ. ИНЖЕНЕРНАЯ ГРАФИКА
Раздел I
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
Тема 1 раздела
ЗАДАНИЕ ТОЧКИ, ПРЯМОЙ, ПЛОСКОСТИ И МНОГОГРАННИКОВ
НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ МОНЖА
Учебные цели - после изучения темы лекции студенты должны:
Знать какие точки прямой называются её следами и алгоритм нахождения следов прямой
Знать, как определить истинную длину прямой и угол наклона её к плоскости проекций способом
прямоугольного треугольника
Знать, как на эпюре изображаются взаимно параллельные, пересекающиеся и скрещивающиеся прямые
Знать, в каком случае прямой угол между прямыми будет проецироваться на плоскость проекций без
искажения
Учебные вопросы лекции:
Следы прямой
Определение истинной длины прямой и угла наклона её к плоскости проекций
Взаимное расположение двух прямых
Проекции прямого угла
Задание на самостоятельную работу:
Изучить, понять и запомнить материал лекции 4
Рекомендуемая учебная литература:
Изучить и запомнить изложенный теоретический материал по конспекту лекций и учебнику: Фролов С.А.
Начертательная геометрия: учебник.- 3-е изд., перераб и доп.- М.:ИНФРА-М, 2008.- (Высшее образование): см. с. 39, 40, 4851, 209
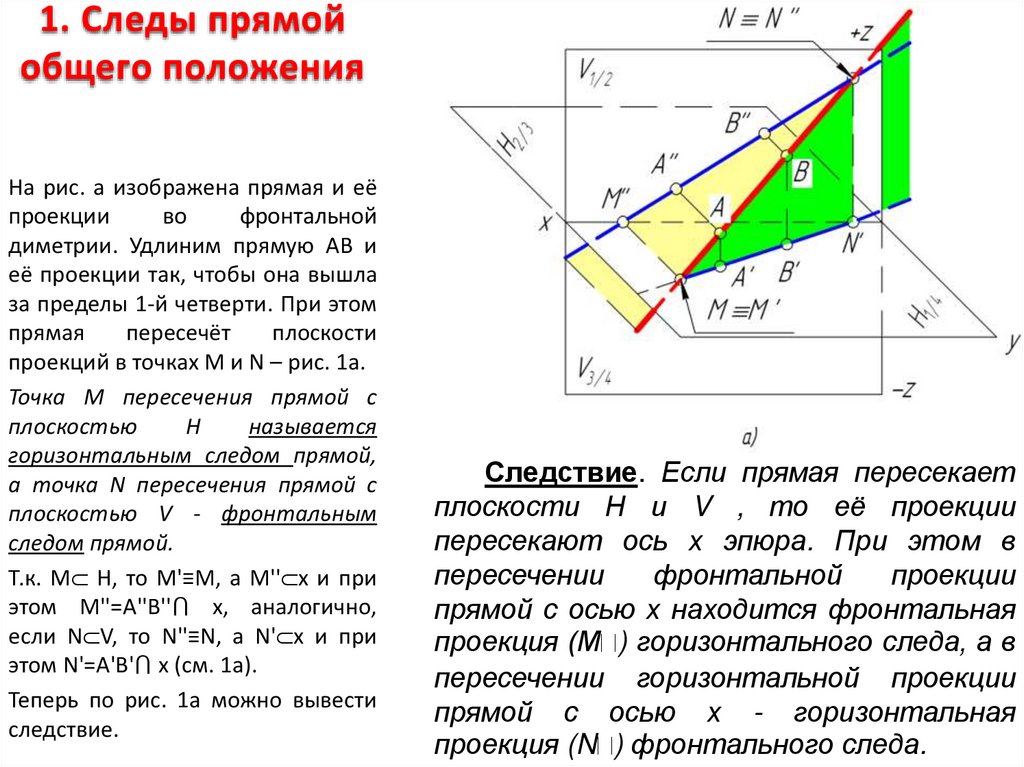
3. 1. Следы прямой общего положения
На рис. a изображена прямая и еёпроекции
во
фронтальной
диметрии. Удлиним прямую АВ и
её проекции так, чтобы она вышла
за пределы 1-й четверти. При этом
прямая
пересечёт
плоскости
проекций в точках М и N – рис. 1a.
Точка М пересечения прямой с
плоскостью
Н
называется
горизонтальным следом прямой,
а точка N пересечения прямой с
плоскостью V - фронтальным
следом прямой.
Т.к. М Н, то М'≡М, а М'' х и при
этом М''=А''В''⋂ х, аналогично,
если N V, то N''≡N, а N' х и при
этом N'=А'В'⋂ х (см. 1a).
Теперь по рис. 1a можно вывести
следствие.
Следствие. Если прямая пересекает
плоскости Н и V , то её проекции
пересекают ось х эпюра. При этом в
пересечении
фронтальной
проекции
прямой с осью х находится фронтальная
проекция (М ) горизонтального следа, а в
пересечении горизонтальной проекции
прямой с осью х - горизонтальная
проекция (N ) фронтального следа.
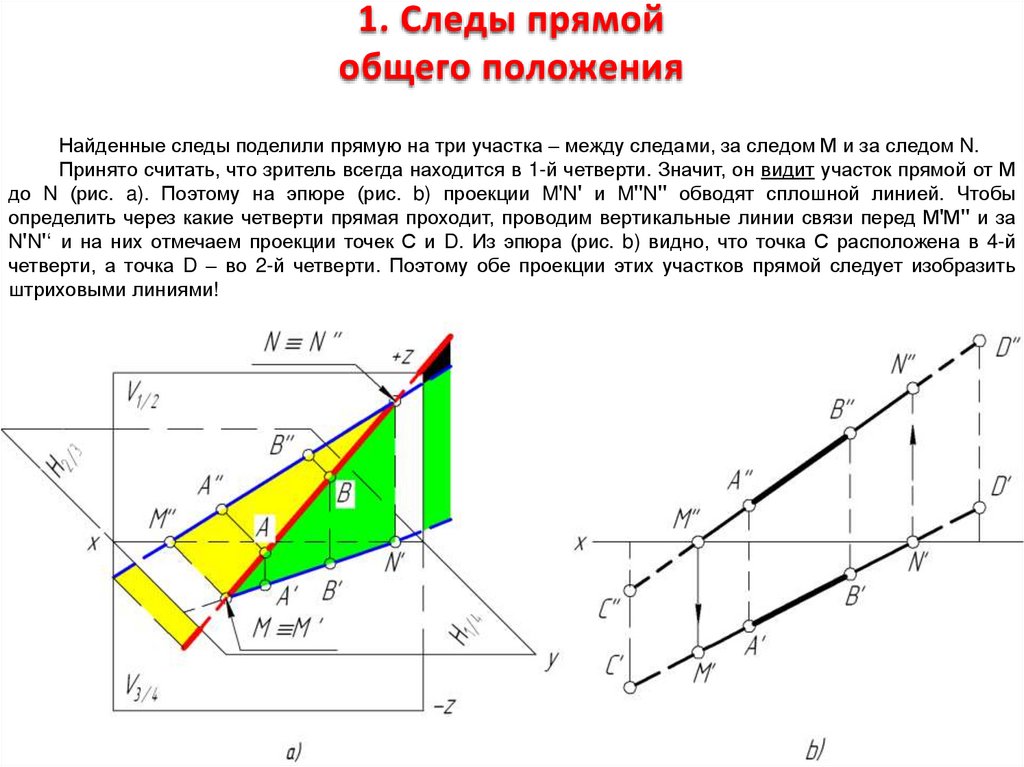
4. 1. Следы прямой общего положения
Найденные следы поделили прямую на три участка – между следами, за следом М и за следом N.Принято считать, что зритель всегда находится в 1-й четверти. Значит, он видит участок прямой от М
до N (рис. a). Поэтому на эпюре (рис. b) проекции M'N' и M''N'' обводят сплошной линией. Чтобы
определить через какие четверти прямая проходит, проводим вертикальные линии связи перед М'М'' и за
N'N'‘ и на них отмечаем проекции точек С и D. Из эпюра (рис. b) видно, что точка С расположена в 4-й
четверти, а точка D – во 2-й четверти. Поэтому обе проекции этих участков прямой следует изобразить
штриховыми линиями!
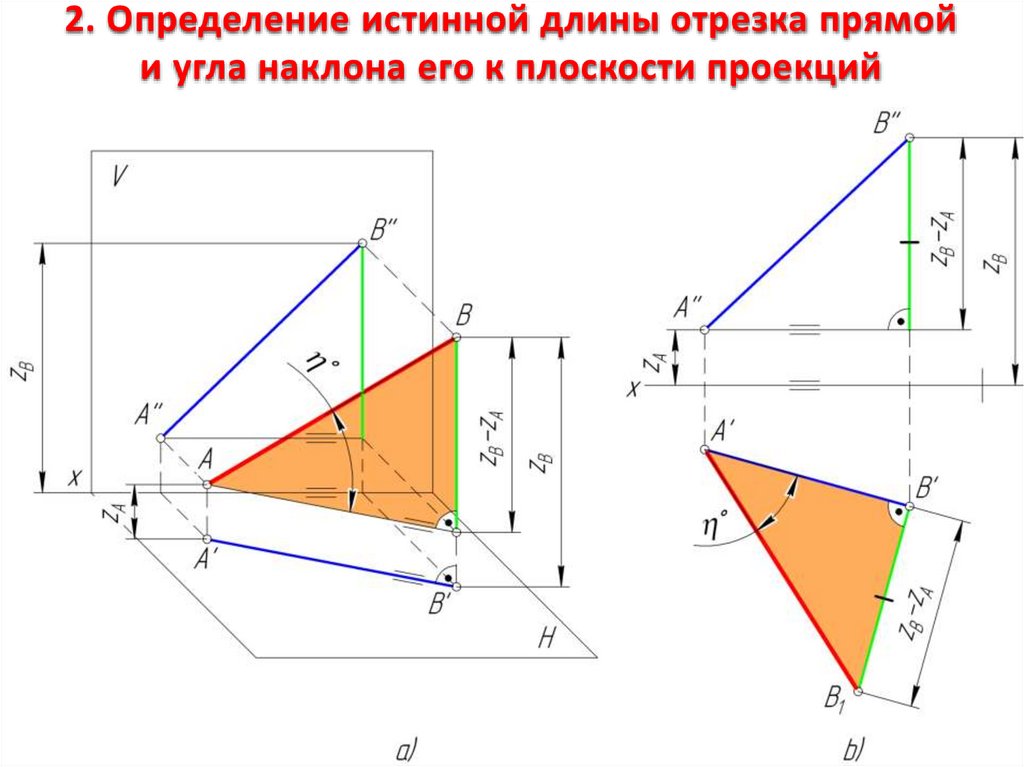
5.
На рис. 2а) во фронтальнойдиметрии показано, из каких
условий составляются размеры
прямоугольного
треугольника,
гипотенуза которого есть длина
отрезка прямой в пространстве.
Следствие. Длина отрезка прямой
равна гипотенузе прямоугольного
треугольника, в котором один
катет есть проекция отрезка, а
второй катет равен разности
расстояний концов отрезка от
той плоскости проекции, на
которой взят первый катет, т.
е. проекция отрезка; угол между
гипотенузой
и
катетомпроекцией равен углу наклона
прямой к той же плоскости
6. 2. Определение истинной длины отрезка прямой и угла наклона его к плоскости проекций
7.
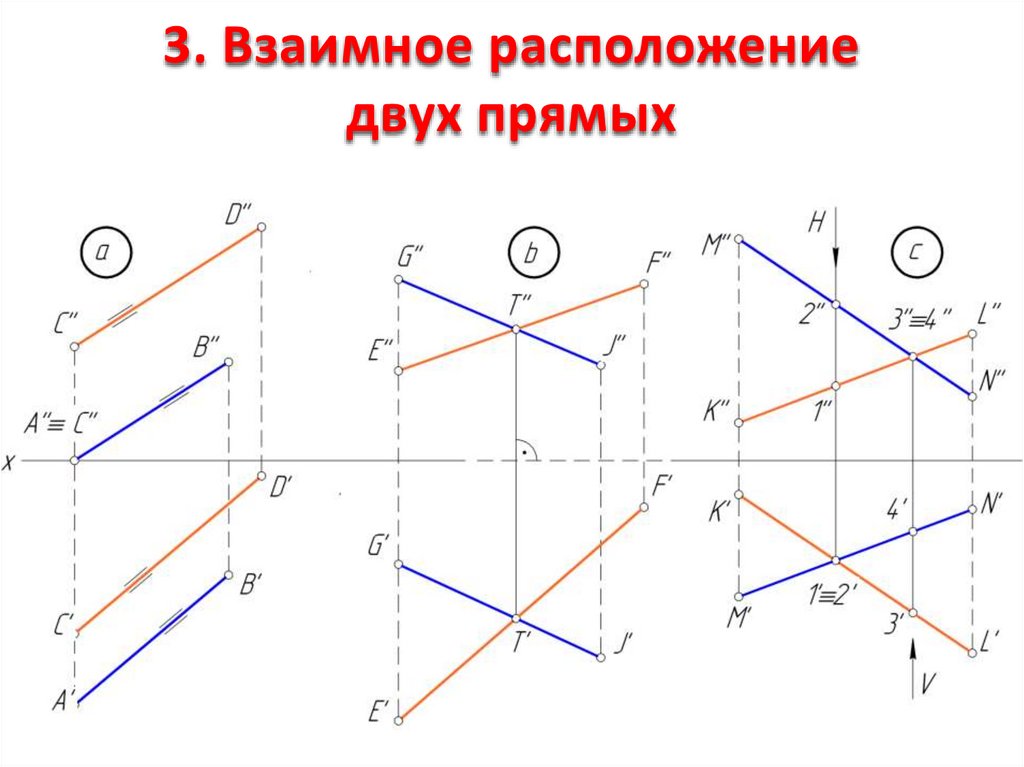
8. 3. Взаимное расположение двух прямых
9.
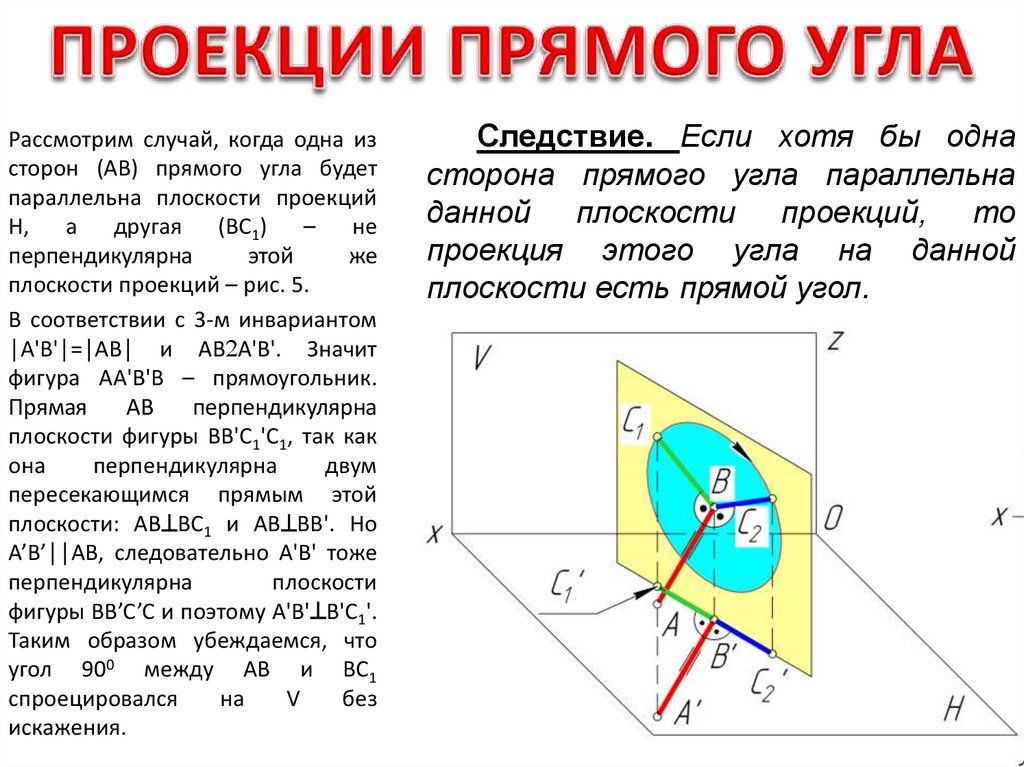
Рассмотрим случай, когда одна изсторон (АВ) прямого угла будет
параллельна плоскости проекций
H, а другая (ВС1) –
не
перпендикулярна
этой
же
плоскости проекций – рис. 5.
В соответствии с 3-м инвариантом
│А'B'│=│AB│ и АВ А'В'. Значит
фигура АА'В'В – прямоугольник.
Прямая
АВ
перпендикулярна
плоскости фигуры BB'C1'C1, так как
она
перпендикулярна
двум
пересекающимся прямым этой
плоскости: АВ ВС1 и АВ ВВ'. Но
А’В’││АВ, следовательно А'В' тоже
перпендикулярна
плоскости
фигуры BB’C’C и поэтому А'В' B'C1'.
Таким образом убеждаемся, что
угол 900 между АВ и ВС1
спроецировался
на
V
без
искажения.
Следствие. Если хотя бы одна
сторона прямого угла параллельна
данной плоскости проекций, то
проекция этого угла на данной
плоскости есть прямой угол.
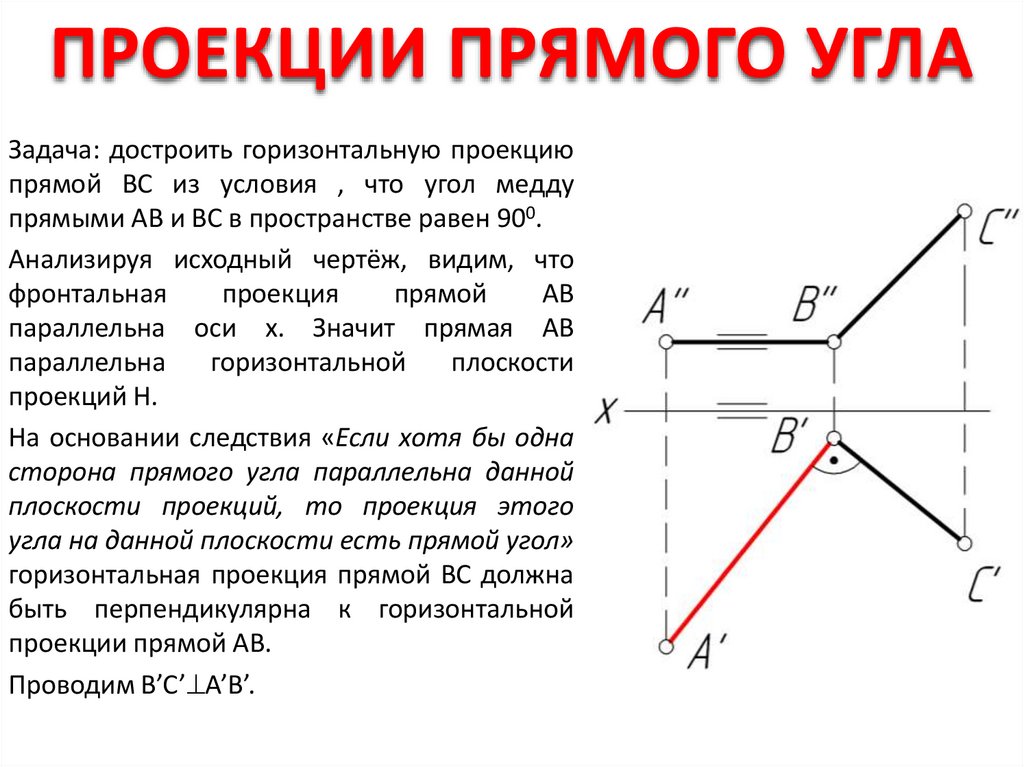
10. ПРОЕКЦИИ ПРЯМОГО УГЛА
Задача: достроить горизонтальную проекциюпрямой ВС из условия , что угол медду
прямыми АВ и ВС в пространстве равен 900.
Анализируя исходный чертёж, видим, что
фронтальная
проекция
прямой
АВ
параллельна оси х. Значит прямая АВ
параллельна
горизонтальной
плоскости
проекций Н.
На основании следствия «Если хотя бы одна
сторона прямого угла параллельна данной
плоскости проекций, то проекция этого
угла на данной плоскости есть прямой угол»
горизонтальная проекция прямой ВС должна
быть перпендикулярна к горизонтальной
проекции прямой АВ.
Проводим В’C’ A’B’.





 drafting
drafting








