Проецирование точки. Способы задания плоскости на чертеже

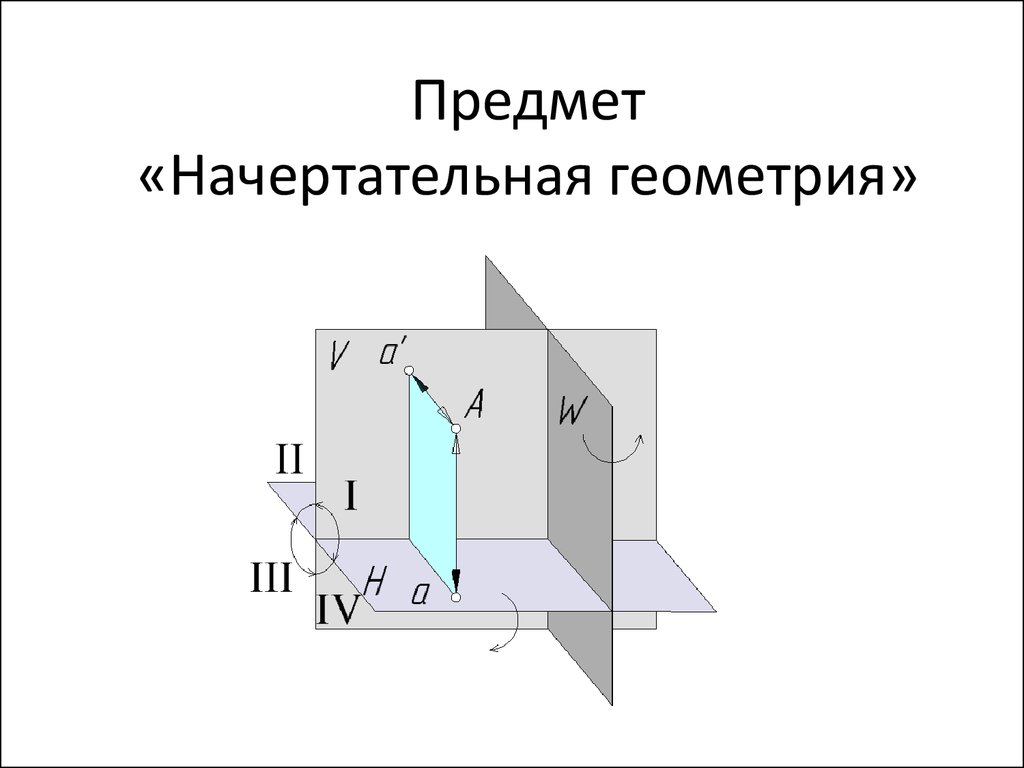
1. Предмет «Начертательная геометрия»

2.

ПРОЕЦИРОВАНИЕ ТОЧКИ

3. ВВЕДЕНИЕ

Чертеж – это своеобразный язык, с помощью
которого, используя всего лишь точки, линии и
ограниченное число геометрических знаков и цифр,
человек имеет возможность изобразить на поверхности
геометрические фигуры (машины, приборы, инженерные
сооружения и т.д.).
Этот графический язык является интернациональным,
он понятен любому технически грамотному человеку,
независим от того, на каком языке он говорит.
Начертательная
геометрия
(НГ)
составляет
теоретическую базу для составления чертежа. Говорят,
“если чертеж – язык техники, то НГ – грамматика
этого языка”.

4. История развития НГ

• НГ возникла в связи с большими потребностями
человечества: из практических задач строительства
различных сооружений, крепостных укреплений, пирамид
и т.д., из запросов машиностроения.
• Леон Батиста Альберти (1404-1472) – итальянский ученый.
Теоретическая разработка основ перспективы; способ
построения перспективы с помощью сетки.
• Лоренцо Гибберти (1378-1455) – итальянский зодчий.
Перенес принципы живописной перспективы на пластическое
изображение в виде рельефа.
• Леонардо да Винчи (1452-1519) – итальянский художник и
скульптор. Примеры применения перспективных изображений, в частности, “наблюдательной” перспективы.

5.

• Альберт Дюрер (1471-1528) – немецкий художник и гравер.
Разработал основы рисования; графические способы
построения плоских и пространственных кривых;
построение перспективы предмета по данным его
горизонтальной и фронтальной проекциям.
• Дезарг (1593-1662) – французский архитектор и математик.
Общий метод изображения предметов в перспективе;
применение для построения перспективы метода
координат – начало аксонометрического метода в НГ.
• Амадео Франсуа Фрезье (1682—1773) - французский ученый
и инженер. Пользовался различными приемами
проецирования, приводил примеры проецирования на две
взаимно перпендикулярные плоскости, для определения
истинного вида фигуры применял способы преобразования
чертежа.

6.

• Возникновение начертательной геометрии как науки
связывают с именем французского математика и инженера
Гаспара Монжа (1746—1818). Выдающиеся способности
позволили сыну торговца скобяными товарами в бургундском
городке Бон, пробившись через все сословные преграды, стать
в 24 года заведующим кафедрами математики и физики в
Королевской военно-инженерной школе в Мезьере, а в 34 года
быть избранным членом Парижской академии наук. В 1795 г. в
Париже для подготовки преподавателей была открыта
Нормальная школа, значительный объем в программе,
которой занимали предметы, связанные с теорией и
практическим приложением начертательной геометрии.
Первый курс начертательной геометрии в этой школе прочел
Монж. Стенограммы его лекций были напечатаны в 1795 г. в
«Журнале Нормальной школы», а в 1799 г. вышли отдельной
книгой. Это был первый учебник, где начертательная
геометрия была заявлена как самостоятельная наука.

7.

• Первым русским ученым, связавшим свою судьбу с
начертательной геометрией, был Яков Александрович
Севастьянов (1796—1849) — профессор Корпуса
инженеров путей сообщения, автор переводных и
оригинальных трудов.
• В 1822 г. курс начертательной геометрии в Казанском
университете читал Н.И. Лобачевский. Однако ведущее
положение в подготовке кадров и развитии начертательной
геометрии в России XIX в. сохранял Корпус инженеров путей
сообщения. Здесь учились, передавали знания следующим
поколениям внесшие заметный вклад в науку:
• А.Х.Редер (1809—1873), Н.П. Дуров (1834—1879), Н.И.
Макаров (1824—1904), В.И. Рынин (1877—1942). 14
классических трудов в области начертательной геометрии
создал Валериан Иванович Курдюмов (1853–1904).

8. Предмет начертательной геометрии.

• Начертательная геометрия – раздел геометрии. Предметом
НГ является изложение и обоснование способов
изображения пространственных фигур (линий, поверхностей
и т.д.) и способов решения задач геометрического характера
по заданным изображениям данной фигуры.
• Цели НГ:
- Научить строить изображения
- Научиться читать эти изображения
- Научиться решать задачи геометрического характера
на этих изображениях
- Развивать пространственное изображение

9. Образование проекций. Методы проецирования.

• В курсе НГ под проецированием понимается отображение
пространственного образа на плоскость, которую называют
плоскостью проекций (ПП).

10.

Центральное проецирование
(Коническое)

11. (

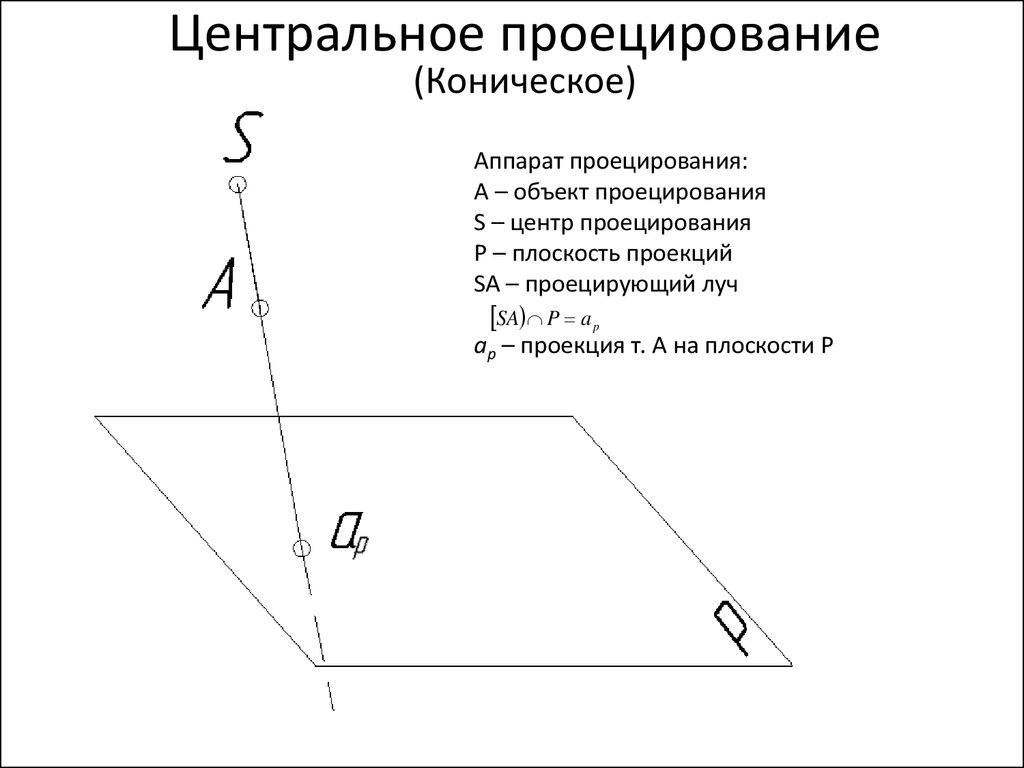
Центральное проецирование
(Коническое)
(
Аппарат проецирования:
А – объект проецирования
S – центр проецирования
Р – плоскость проекций
SA – проецирующий луч
SA P a p
ap – проекция т. А на плоскости Р

12. Свойства проецирования:

• Проекцией точки называют точку пересечения
проецирующего луча с ПП.
• Каждая точка пространства имеет единственную свою
проекцию на ПП.
• Каждая точка на ПП может быть проекцией множества
точек пространства, расположенных на проецирующем
луче.
• Одна проекция точки не определяет однозначно ее
положения в пространстве.

13.

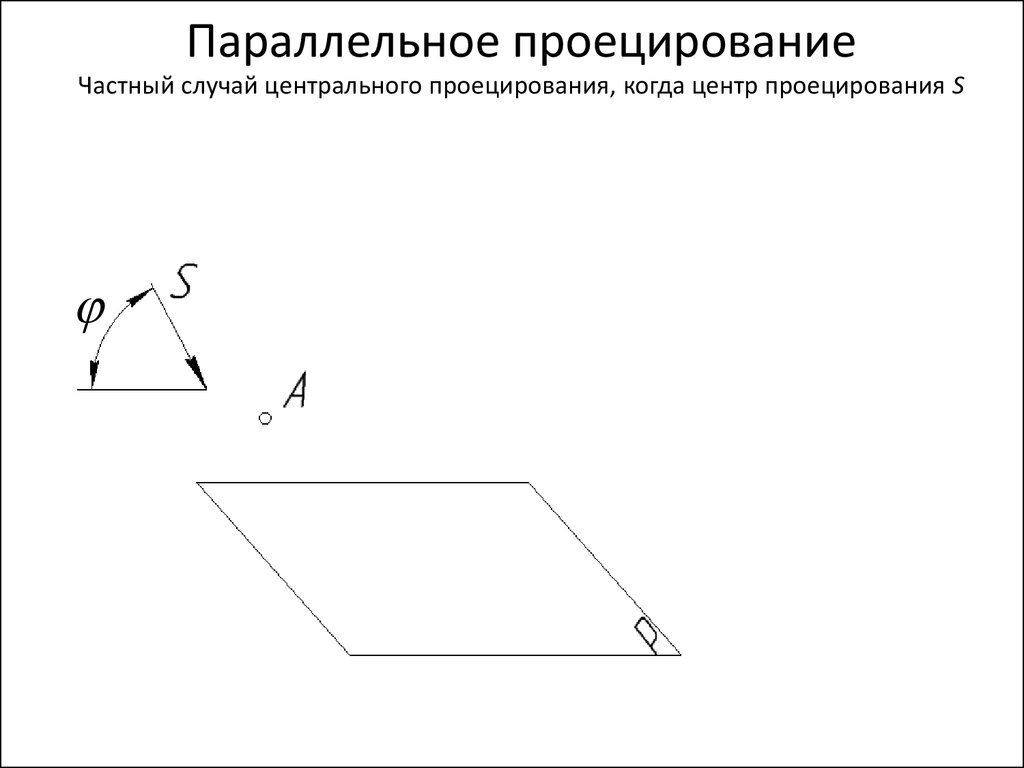
Параллельное проецирование
Частный случай центрального проецирования, когда центр проецирования S

14.

Параллельное проецирование
Частный случай центрального проецирования, когда центр проецирования S
Аппарат проецирования:
А – объект проецирования
S – направление проецирования
Р – плоскость проекций

15.

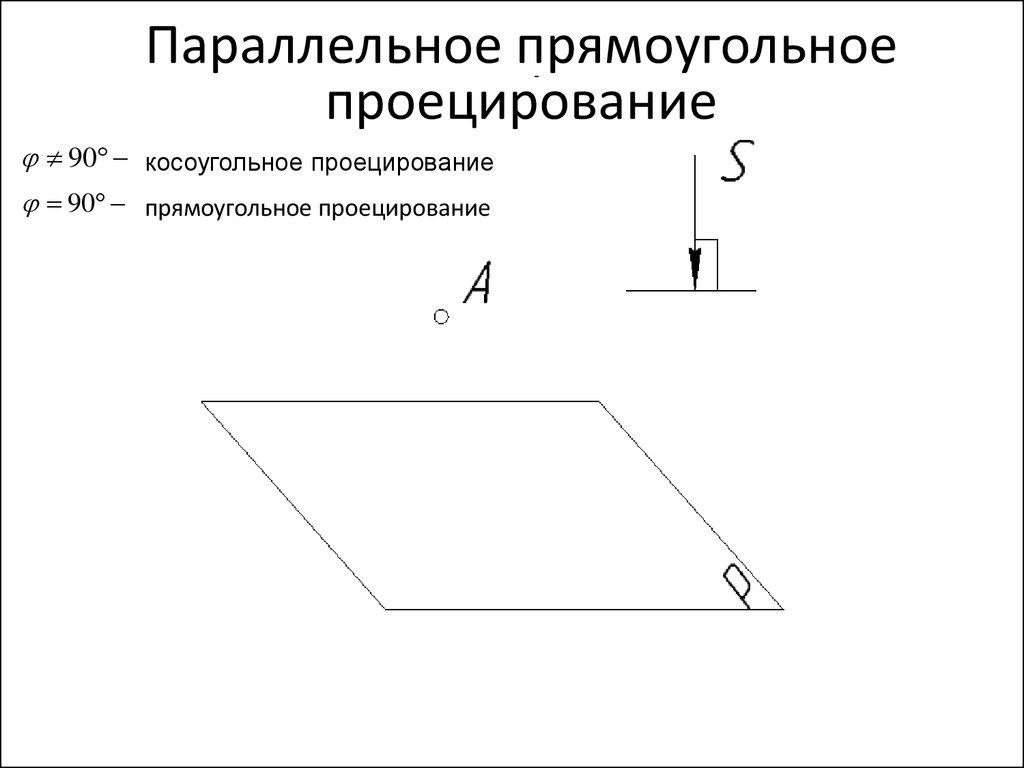
Параллельное прямоугольное
проецирование
-
90 косоугольное проецирование
90 прямоугольное проецирование

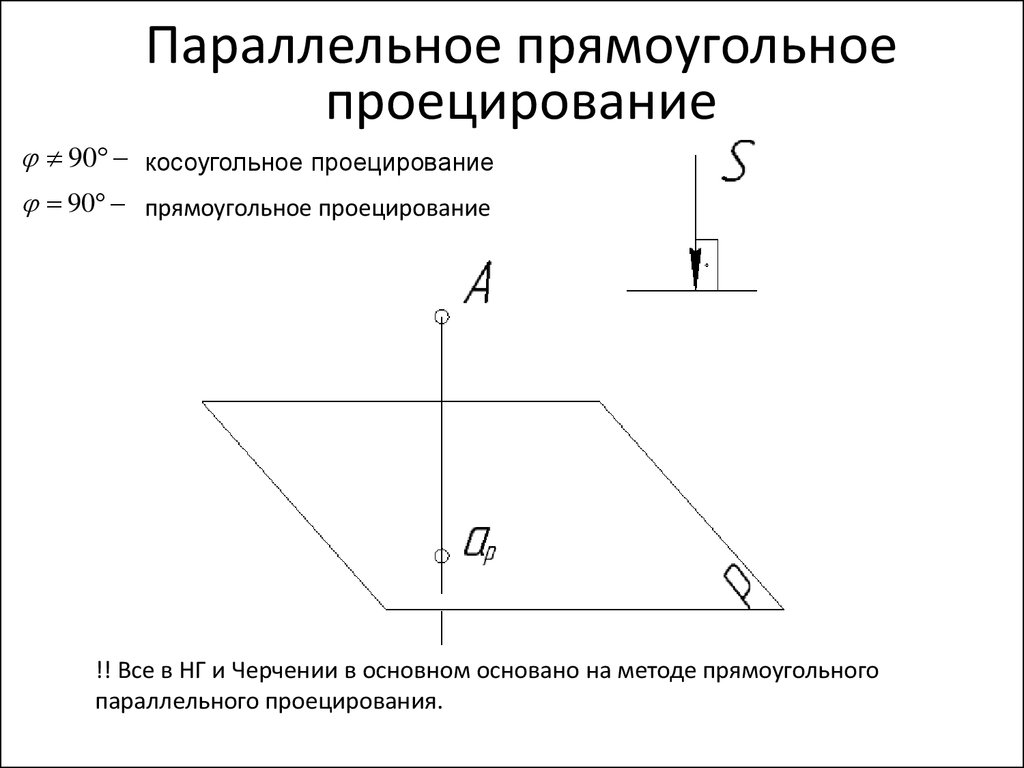
16.

Параллельное прямоугольное
проецирование
90 косоугольное проецирование
90 прямоугольное проецирование
!! Все в НГ и Черчении в основном основано на методе прямоугольного
параллельного проецирования.

17.

Проецирование точки на две взаимноперпендикулярные ПП
• Для получения ортогонального чертежа
обладающего свойством “обратимости”
необходимо иметь, по крайней мере, две
связанные между собой ортогональные
проекции объекта.
• В трудах, опубликованных Г. Монжем в 1799
году, предлагалось использовать систему двух
взаимно перпендикулярных плоскостей
проекций. Линия пересечения плоскостей Н и
V называется осью проекций (x).

18.

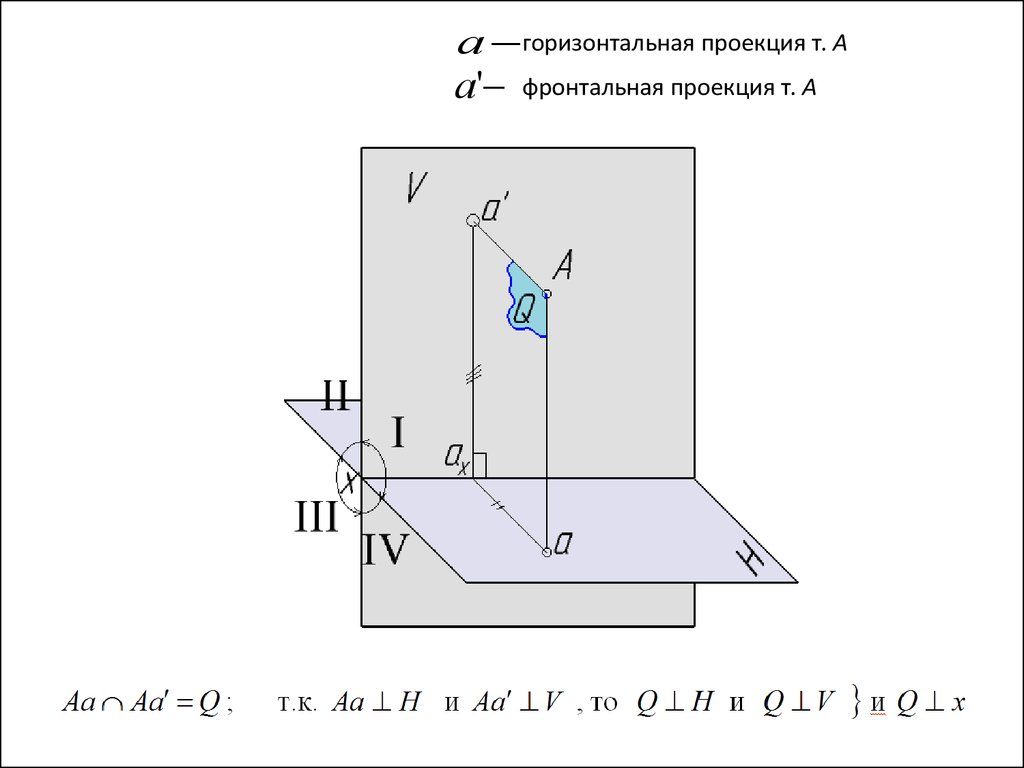
19.

Н - горизонтальной плоскостью проекций (расположена горизонтально)
V - фронтальной плоскостью проекций (расположена вертикально)
V H x - ось проекций
I четверть – над Н перед V;
III четверть - под Н за V;
II четверть – над Н за V;
IV четверть - под Н перед V;

20.

а горизонтальная проекция т. А
а'
фронтальная проекция т. А

21.

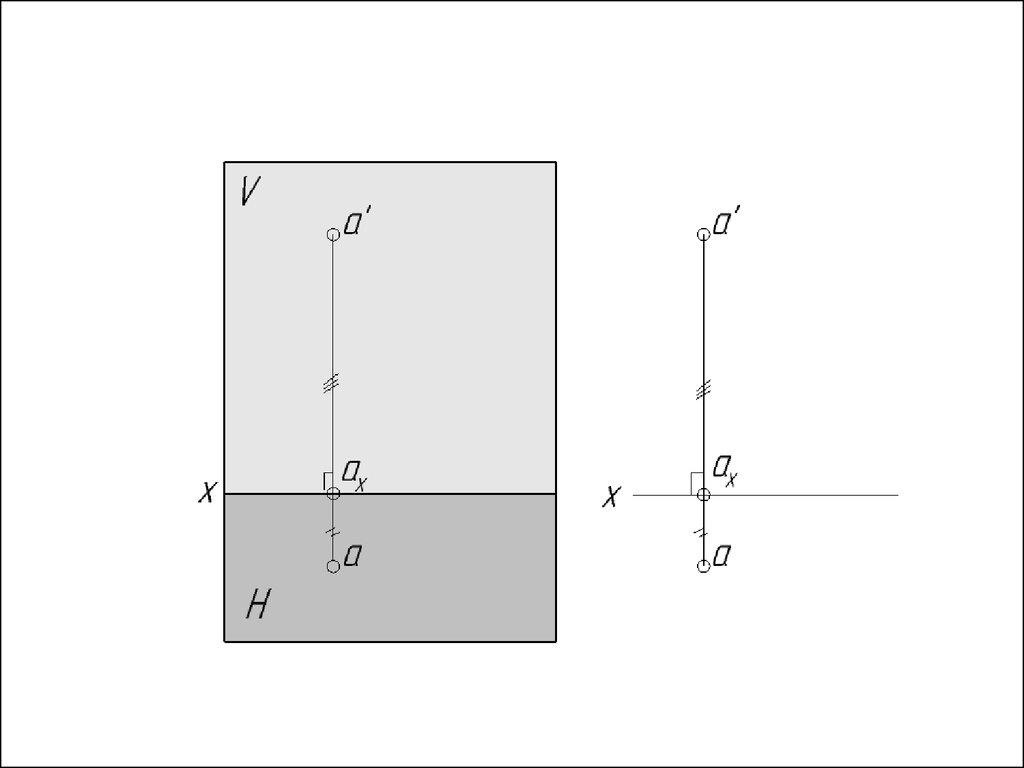
• Теорема: проекции некоторой точки получаются
расположенными на прямых перпендикулярных к
оси проекций и пересекающих эту ось в одной и той
же точке:
• Для получения изображений на плоскости Г. Монж
предложил совместить ПП в одну плоскость,
совпадающую с плоскостью чертежа – эпюра
Монжа. При этом фронтальная плоскость проекций
остается неподвижной, а горизонтальная
вращением вокруг оси x совмещается с плоскостью
чертежа. (Обратим внимание: задняя полуплоскость
Н при этом поднимается.)
• При этом фронтальная и горизонтальная
проекции точки располагаются на одной прямой,
перпендикулярной к оси проекцийпрямой
- линия связи.

22.

23.

24. Проецирование точки на три взаимно-перпендикулярные ПП

В практике составления чертежа изделия зачастую необходимо не две,
а три и более число проекций.
Помимо горизонтальной и фронтальной плоскостей проекций зачастую
используется и третья плоскость проекций, которая перпендикулярна к
плоскостям V и Н - профильная плоскость проекций W.

25.

Три взаимно перпендикулярные плоскости попарно пересекаются по трем прямым осям проекций x, y и z, пересекающихся в точке О. Плоскости V, Н и W делят
пространство на 8 октантов.
Для получения проекций точки А в системе трех плоскостей проекций необходимо
осуществить прямоугольное проецирование на плоскости Н, V и W.

26.

27.

28.

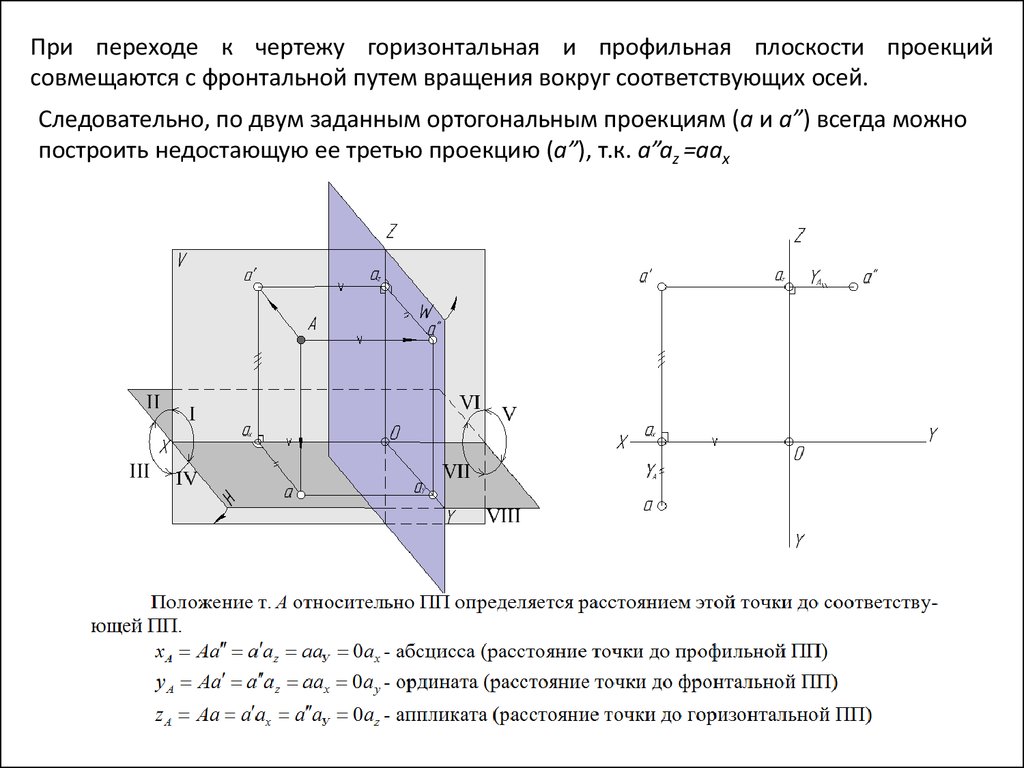
При переходе к чертежу горизонтальная и профильная плоскости проекций
совмещаются с фронтальной путем вращения вокруг соответствующих осей.
Следовательно, по двум заданным ортогональным проекциям (a и a”) всегда можно
построить недостающую ее третью проекцию (a”), т.к. a”az =aax

29.

Пример: построить проекции точки в осной и безосной системах по ее
прямоугольным координатам А(30, 15, 40).
Алгоритм построения проекций точки:

30.

Пример: построить проекции точки в осной и безосной системах по ее
прямоугольным координатам А(30, 15, 40).
Алгоритм построения проекций точки:
1). По координате Х откладываем ХА= 30 мм

31.

Пример: построить проекции точки в осной и безосной системах по ее
прямоугольным координатам А(30, 15, 40).
Алгоритм построения проекций точки:
1). По координате Х откладываем ХА= 30 мм
2). Проводим линию связи
3). По координате Y откладываем YA= 15 мм

32.

Пример: построить проекции точки в осной и безосной системах по ее
прямоугольным координатам А(30, 15, 40).
Алгоритм построения проекций точки:
1). По координате Х откладываем ХА= 30 мм
2). Проводим линию связи
3). По координате Y откладываем YA= 15 мм
4). По координате Z откладываем ZA= 40 мм

33.

Пример: построить проекции точки в осной и безосной системах по ее
прямоугольным координатам А(30, 15, 40).
Алгоритм построения проекций точки:
1). По координате Х откладываем ХА= 30 мм
2). Проводим линию связи
3). По координате Y откладываем YA= 15 мм
4). По координате Z откладываем ZA= 40 мм
5). Координатным методом определяем
профильную проекцию a”az =aax

34.

ПРЕЦИРОВАНИЕ ПРЯМОЙ

35.

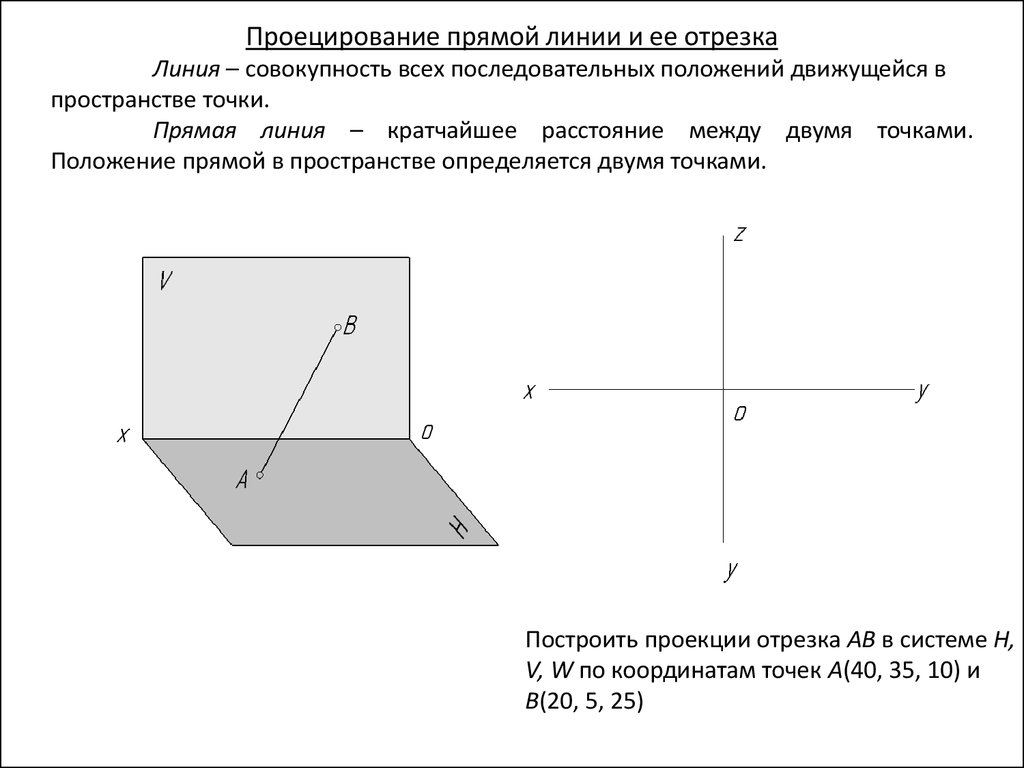
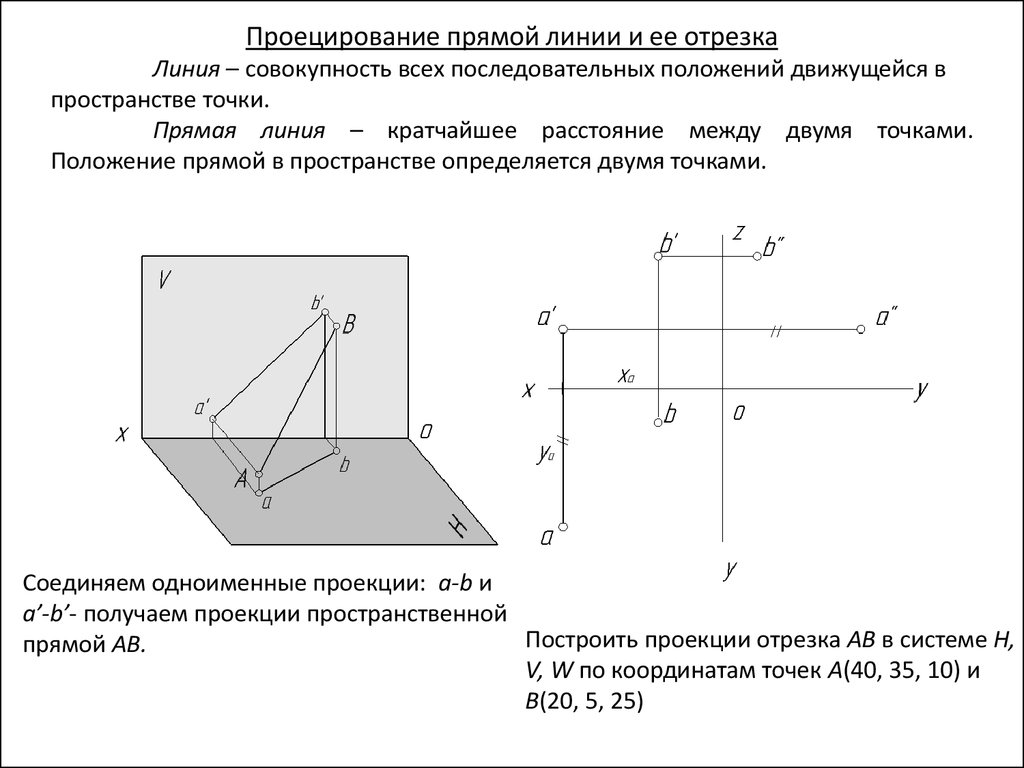
Проецирование прямой линии и ее отрезка
Линия – совокупность всех последовательных положений движущейся в
пространстве точки.
Прямая линия – кратчайшее расстояние между двумя точками.
Положение прямой в пространстве определяется двумя точками.
Построить проекции отрезка АВ в системе H,
V, W по координатам точек А(40, 35, 10) и
В(20, 5, 25)

36.

Проецирование прямой линии и ее отрезка
Линия – совокупность всех последовательных положений движущейся в
пространстве точки.
Прямая линия – кратчайшее расстояние между двумя точками.
Положение прямой в пространстве определяется двумя точками.
Построить проекции отрезка АВ в системе H,
V, W по координатам точек А(40, 35, 10) и
В(20, 5, 25)

37.

Проецирование прямой линии и ее отрезка
Линия – совокупность всех последовательных положений движущейся в
пространстве точки.
Прямая линия – кратчайшее расстояние между двумя точками.
Положение прямой в пространстве определяется двумя точками.
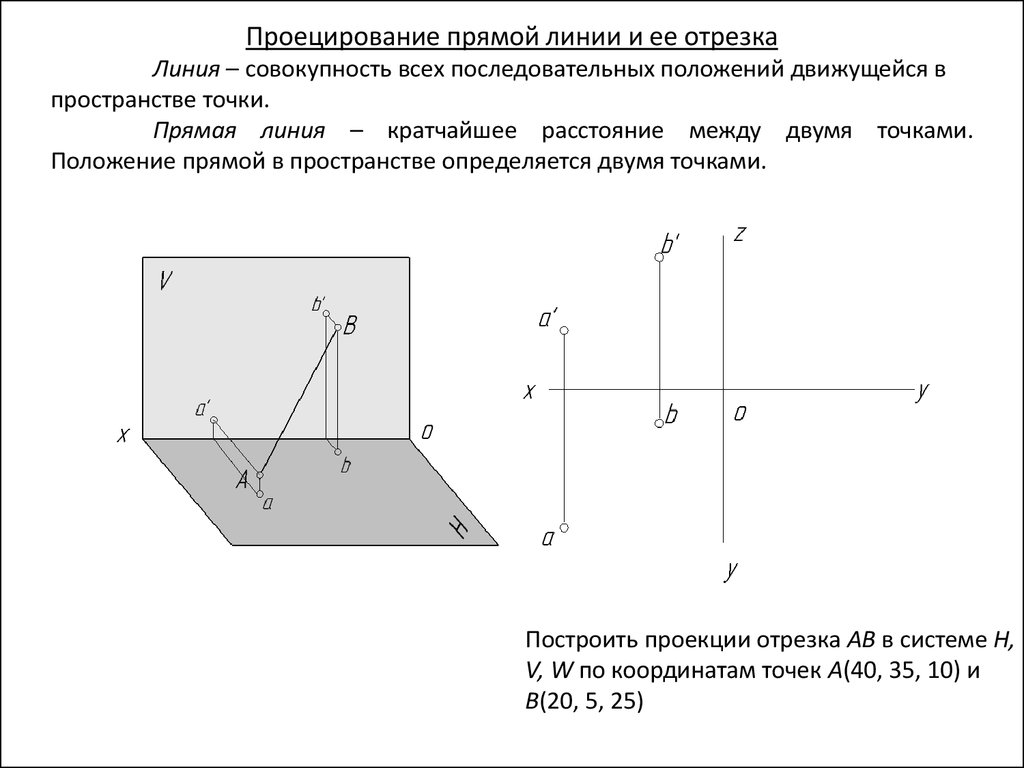
Соединяем одноименные проекции: a-b и
a’-b’- получаем проекции пространственной
Построить проекции отрезка АВ в системе H,
прямой АВ.
V, W по координатам точек А(40, 35, 10) и
В(20, 5, 25)

38.

Проецирование прямой линии и ее отрезка
Линия – совокупность всех последовательных положений движущейся в
пространстве точки.
Прямая линия – кратчайшее расстояние между двумя точками.
Положение прямой в пространстве определяется двумя точками.
Соединяем одноименные проекции: a-b и
a’-b’- получаем проекции пространственной
Построить проекции отрезка АВ в системе H,
прямой АВ.
V, W по координатам точек А(40, 35, 10) и
В(20, 5, 25)

39.

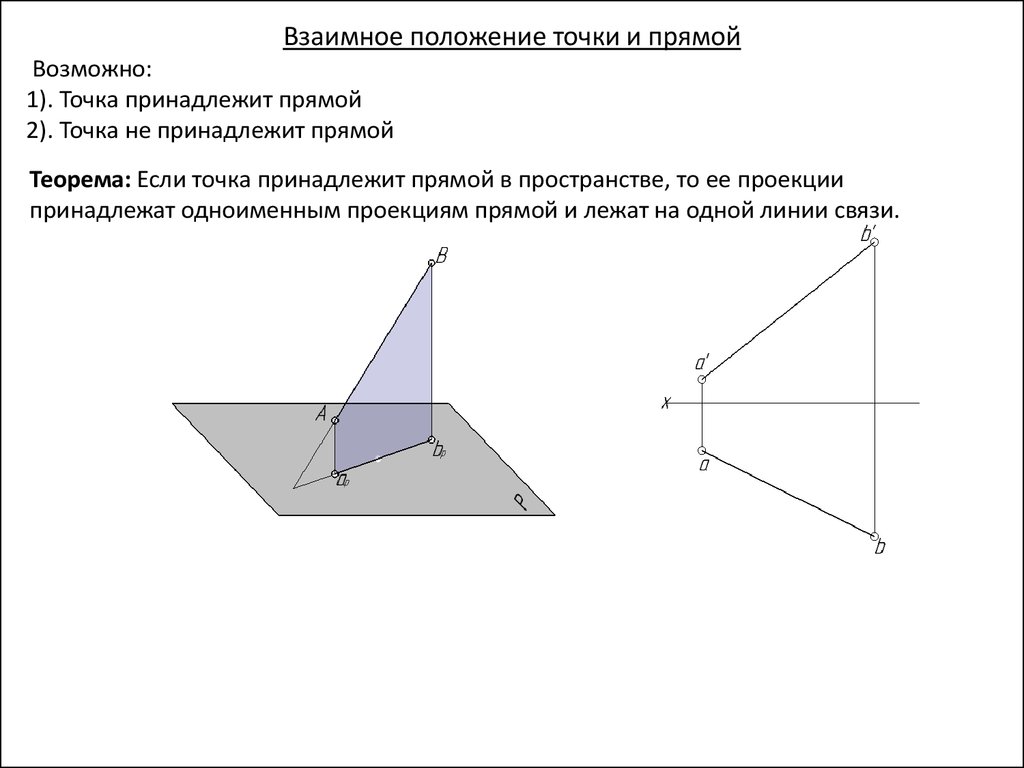
Взаимное положение точки и прямой
Возможно:
1). Точка принадлежит прямой
2). Точка не принадлежит прямой
Теорема: Если точка принадлежит прямой в пространстве, то ее проекции
принадлежат одноименным проекциям прямой и лежат на одной линии связи.

40.

Взаимное положение точки и прямой
Возможно:
1). Точка принадлежит прямой
2). Точка не принадлежит прямой
Теорема: Если точка принадлежит прямой в пространстве, то ее проекции
принадлежат одноименным проекциям прямой и лежат на одной линии связи.

41.

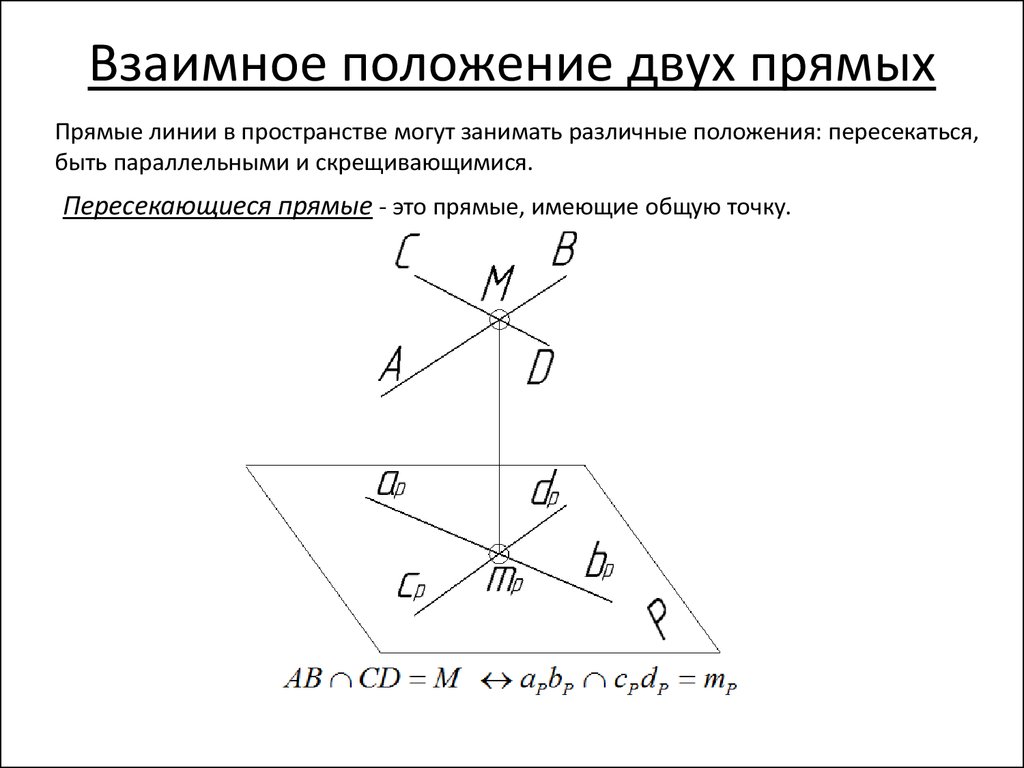
ВЗАИМНОЕ ПОЛОЖЕНИЕ ПРЯМЫХ

42. Взаимное положение двух прямых

Прямые линии в пространстве могут занимать различные положения: пересекаться,
быть параллельными и скрещивающимися.
Пересекающиеся прямые - это прямые, имеющие общую точку.

43.

44.

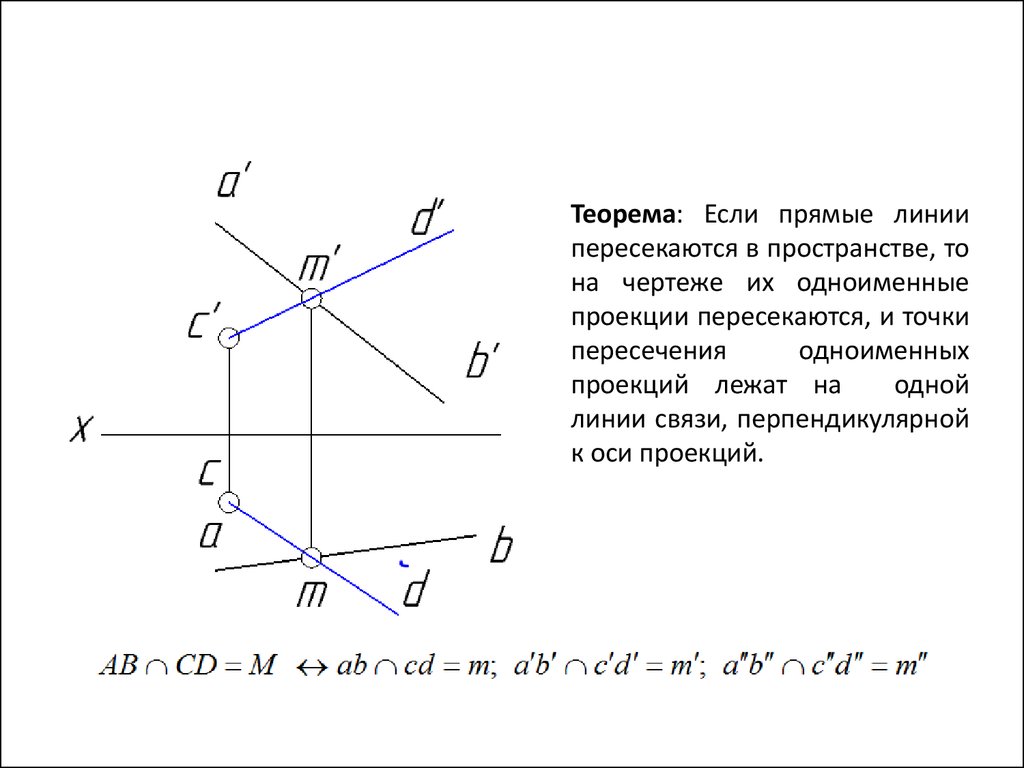
Теорема: Если прямые линии
пересекаются в пространстве, то
на чертеже их одноименные
проекции пересекаются, и точки
пересечения
одноименных
проекций лежат на
одной
линии связи, перпендикулярной
к оси проекций.

45.

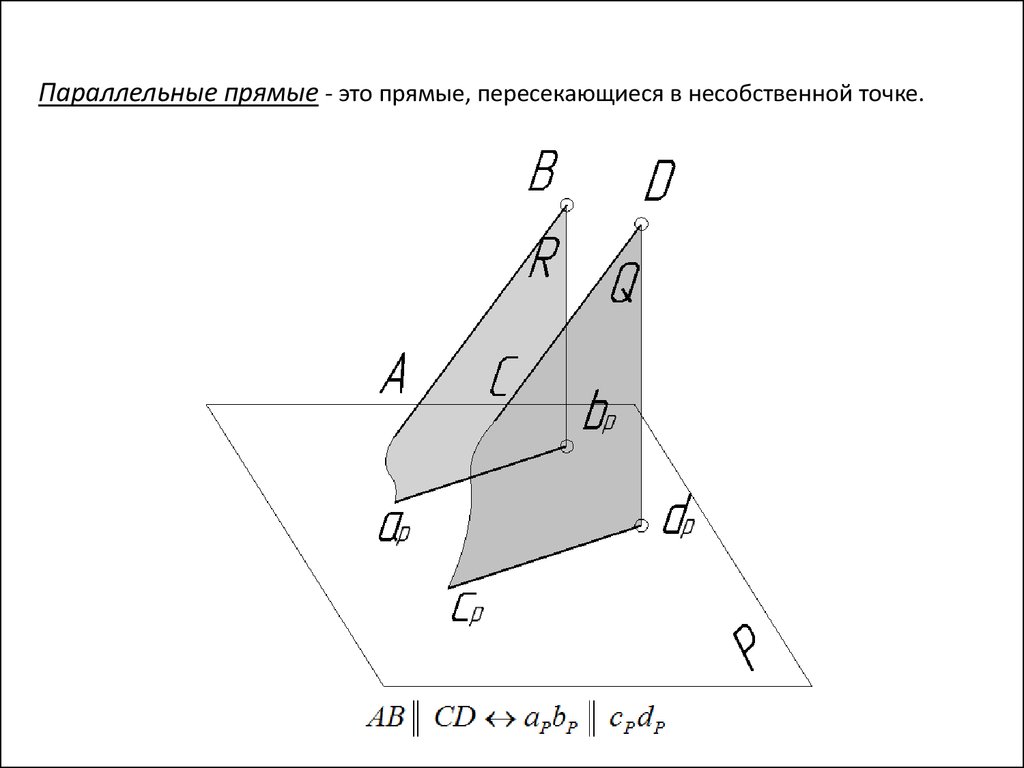
Параллельные прямые - это прямые, пересекающиеся в несобственной точке.

46.

Теорема: Если прямые линии
параллельны в пространстве,
то
на
чертеже
их
одноименные
проекции
также параллельны

47.

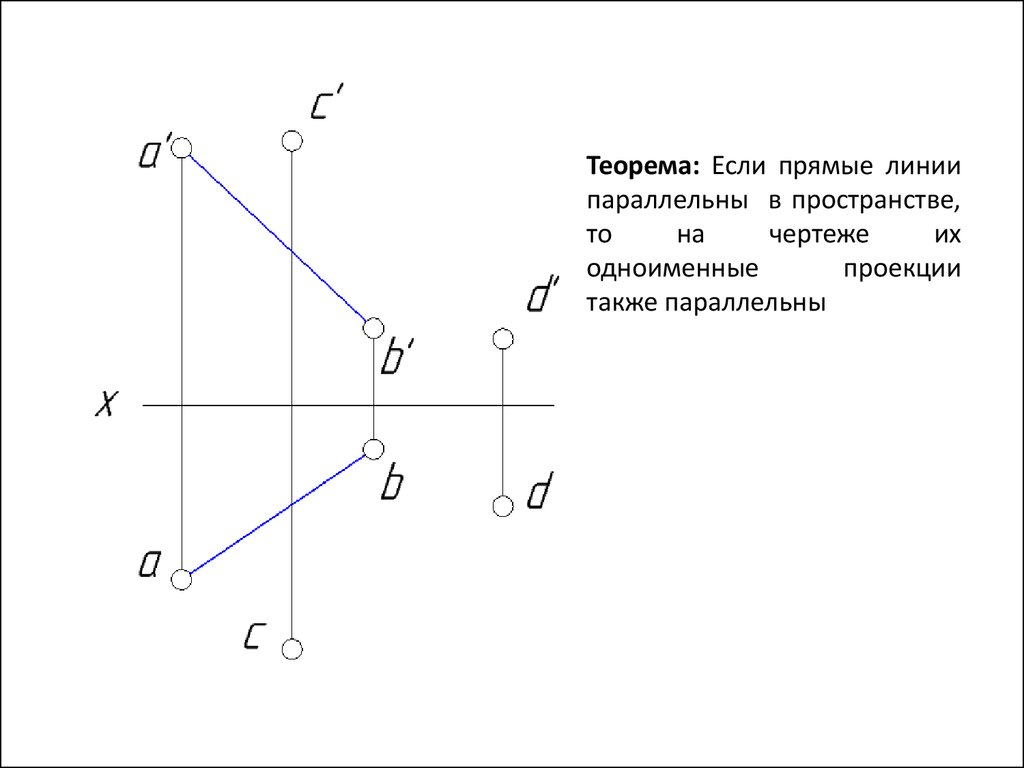
Теорема: Если прямые линии
параллельны в пространстве,
то
на
чертеже
их
одноименные
проекции
также параллельны

48.

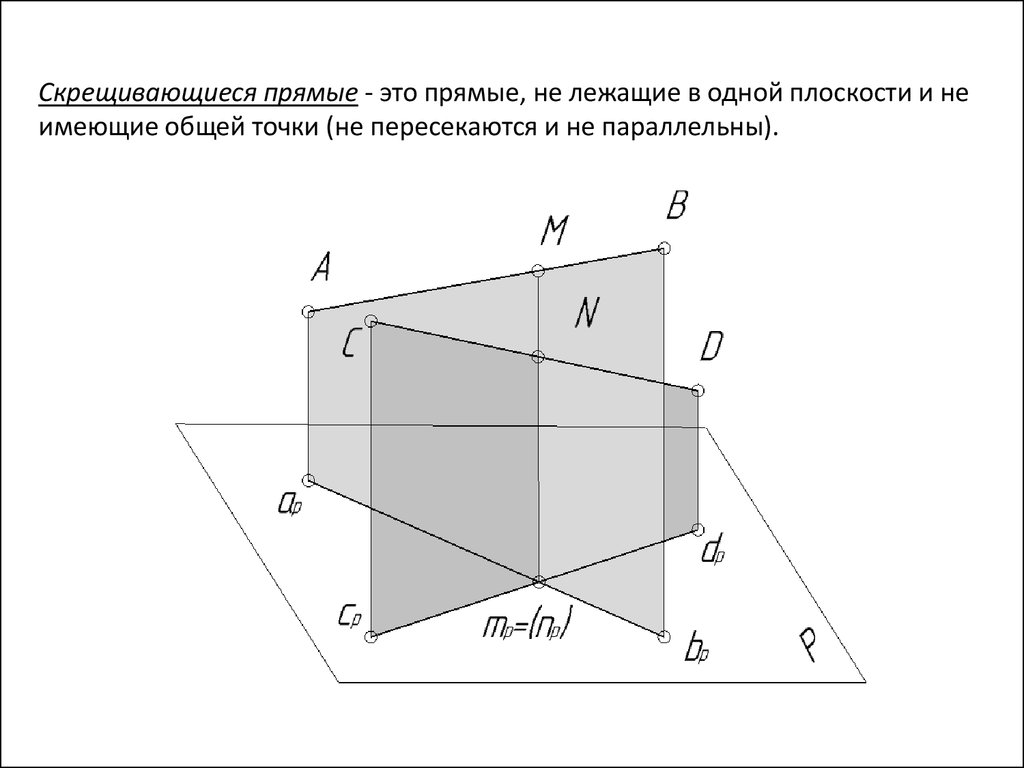
Скрещивающиеся прямые - это прямые, не лежащие в одной плоскости и не
имеющие общей точки (не пересекаются и не параллельны).

49.

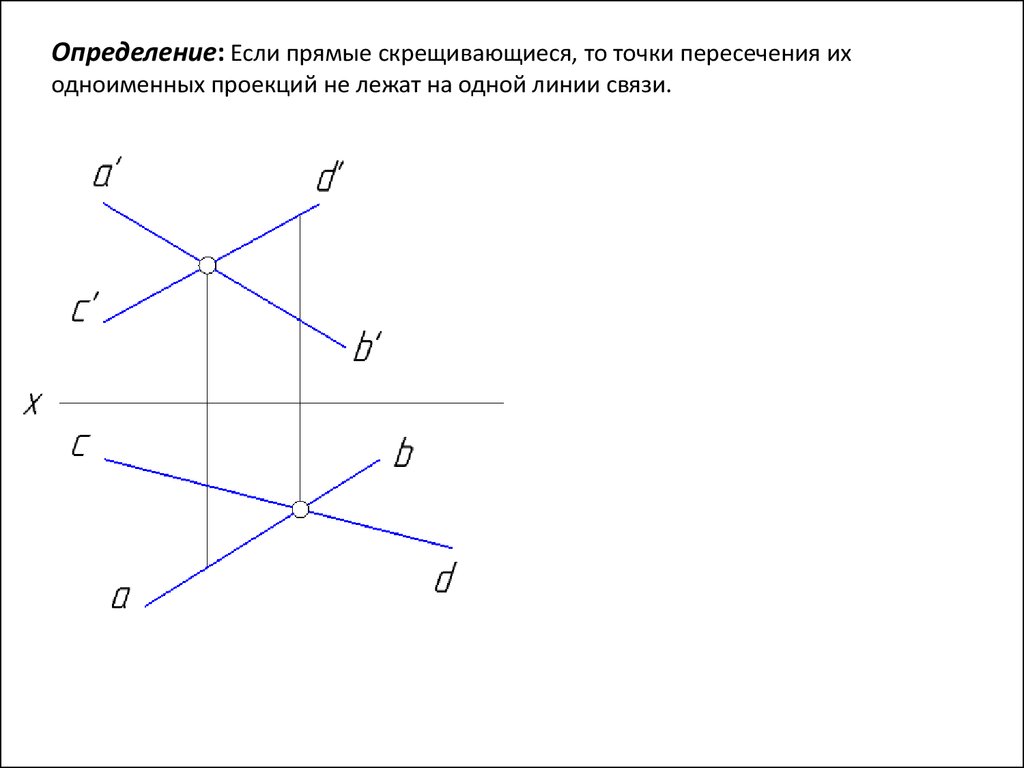
Определение: Если прямые скрещивающиеся, то точки пересечения их
одноименных проекций не лежат на одной линии связи.

50.

Определение: Если прямые скрещивающиеся, то точки пересечения их
одноименных проекций не лежат на одной линии связи.
Точки пресечения одноименных проекций
(например, m и n) представляют проекции
двух точек принадлежащих разным
прямым:
• точка с проекциями m и m’ принадлежит
прямой AB
• точка с проекциями n и n’ принадлежит
прямой CD
• Эти точки одинаково удалены от
плоскости V , но по-разному от плоскости
H.
Они принадлежат одному горизонтальнопроецирующему лучу и имеют разные
аппликаты.
Эти точки называются “конкурирующими”.
Проекция одной из конкурирующих точек
наиболее удаленной от ПП считается
“невидимой”.

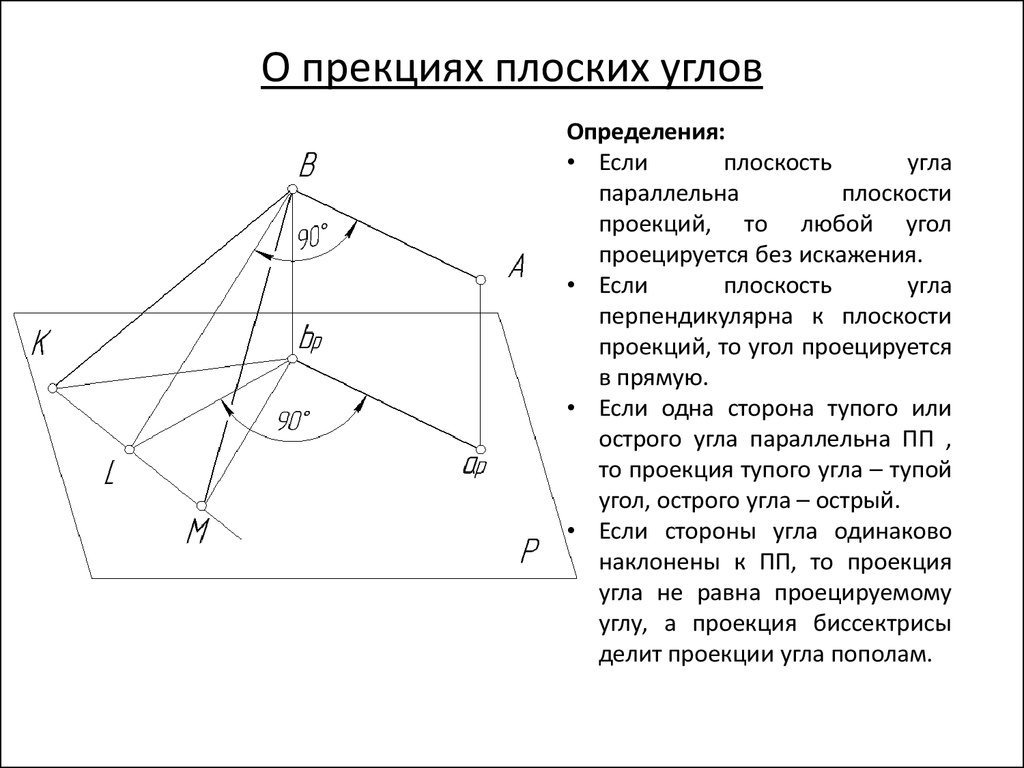
51. О прекциях плоских углов

Определения:
• Если
плоскость
угла
параллельна
плоскости
проекций, то любой угол
проецируется без искажения.
• Если
плоскость
угла
перпендикулярна к плоскости
проекций, то угол проецируется
в прямую.
• Если одна сторона тупого или
острого угла параллельна ПП ,
то проекция тупого угла – тупой
угол, острого угла – острый.
• Если стороны угла одинаково
наклонены к ПП, то проекция
угла не равна проецируемому
углу, а проекция биссектрисы
делит проекции угла пополам.

52.

!Частный случай проецирования прямого угла
Теорема:
Если
плоскость
прямого
угла
не
перпендикулярна к плоскости
проекций, а хотя бы одна из
сторон угла параллельна этой
плоскости, то прямой угол
проецируется на нее в виде
прямого же угла.
Или
Теорема: Если одна из сторон
прямого угла параллельна
плоскости проекций, а другая
ей не перпендикулярна, то
прямой угол на эту плоскость
проецируется в виде прямого
же угла.

53.

!Частный случай проецирования прямого угла

54.

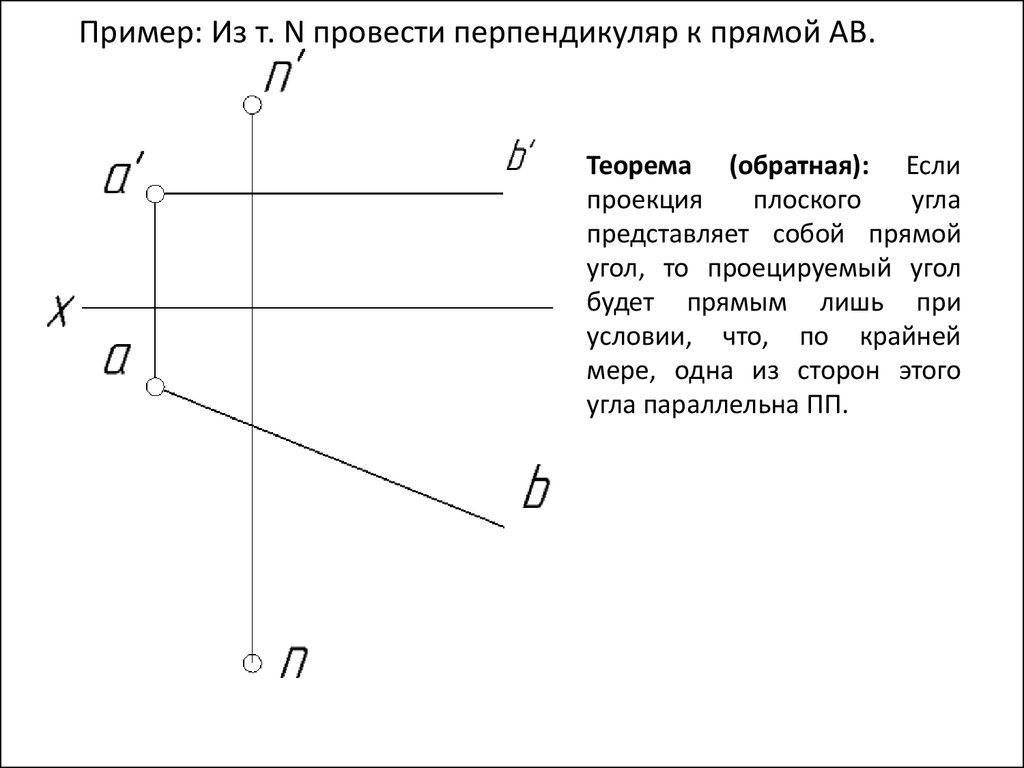
Пример: Из т. N провести перпендикуляр к прямой АВ.
Теорема (обратная): Если
проекция
плоского
угла
представляет собой прямой
угол, то проецируемый угол
будет прямым лишь при
условии, что, по крайней
мере, одна из сторон этого
угла параллельна ПП.

55.

Пример: Из т. N провести перпендикуляр к прямой АВ.
Теорема (обратная): Если
проекция
плоского
угла
представляет собой прямой
угол, то проецируемый угол
будет прямым лишь при
условии, что, по крайней
мере, одна из сторон этого
угла параллельна ПП.
Т.к. прямая АВ параллельна плоскости Н, то прямой угол отобразится без
искажения (в прямой) именно на эту плоскость: akn = AKN = 900

56.

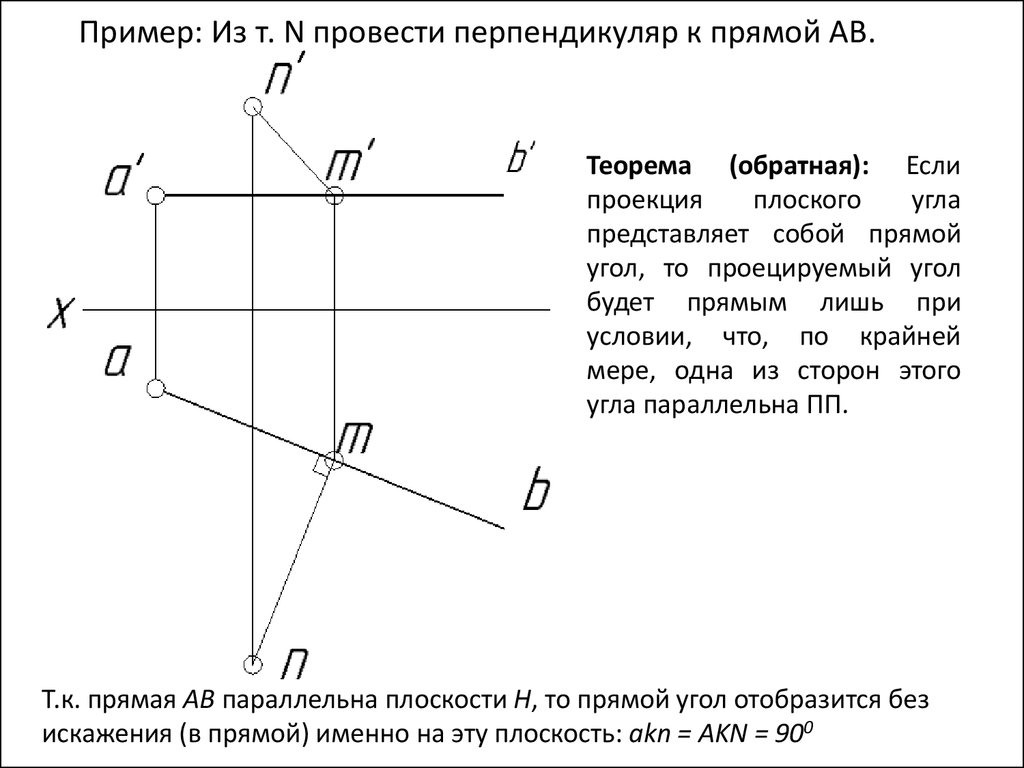
Пример: Из т. N провести перпендикуляр к прямой АВ.
Теорема (обратная): Если
проекция
плоского
угла
представляет собой прямой
угол, то проецируемый угол
будет прямым лишь при
условии, что, по крайней
мере, одна из сторон этого
угла параллельна ПП.
Т.к. прямая АВ параллельна плоскости Н, то прямой угол отобразится без
искажения (в прямой) именно на эту плоскость: akn = AKN = 900

57.

ПЛОСКОСТЬ

58. ПЛОСКОСТЬ

• Поверхность
–
совокупность
всех
последовательных положений движущейся в
пространстве линии.
• В ВМ плоскость является простейшей
поверхностью – поверхность первого порядка
• В НГ плоскость представляют как предельное
понятие ровности или как бесконечная
поверхность, имеющая на всем протяжении
одинаковое направление.

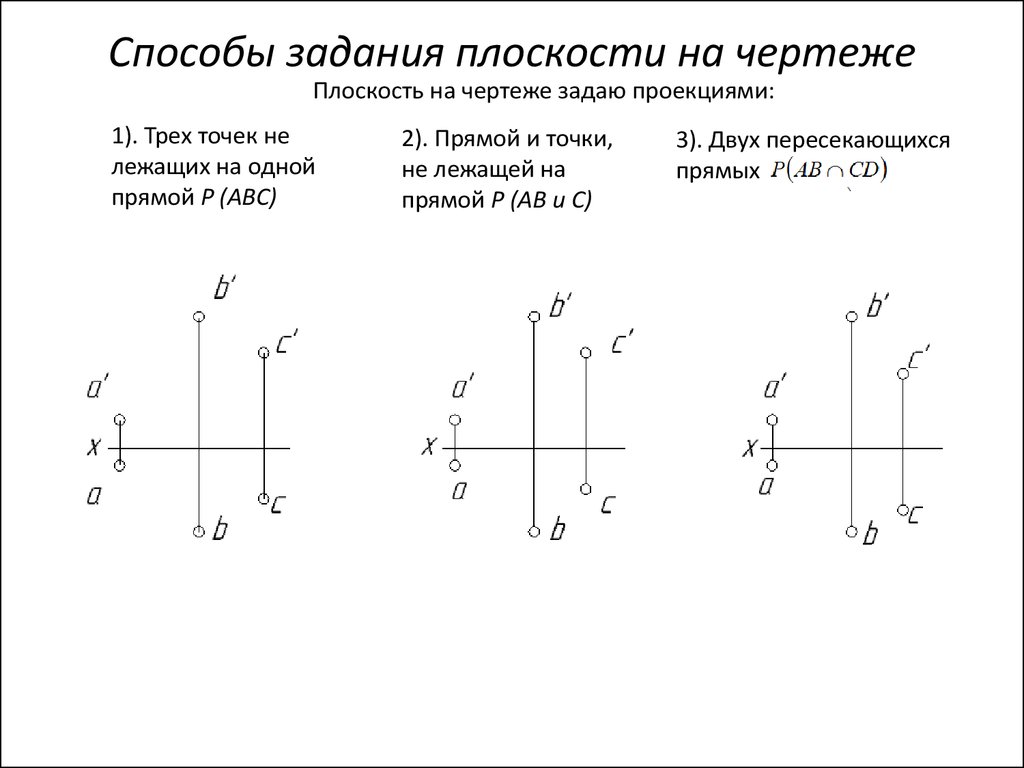
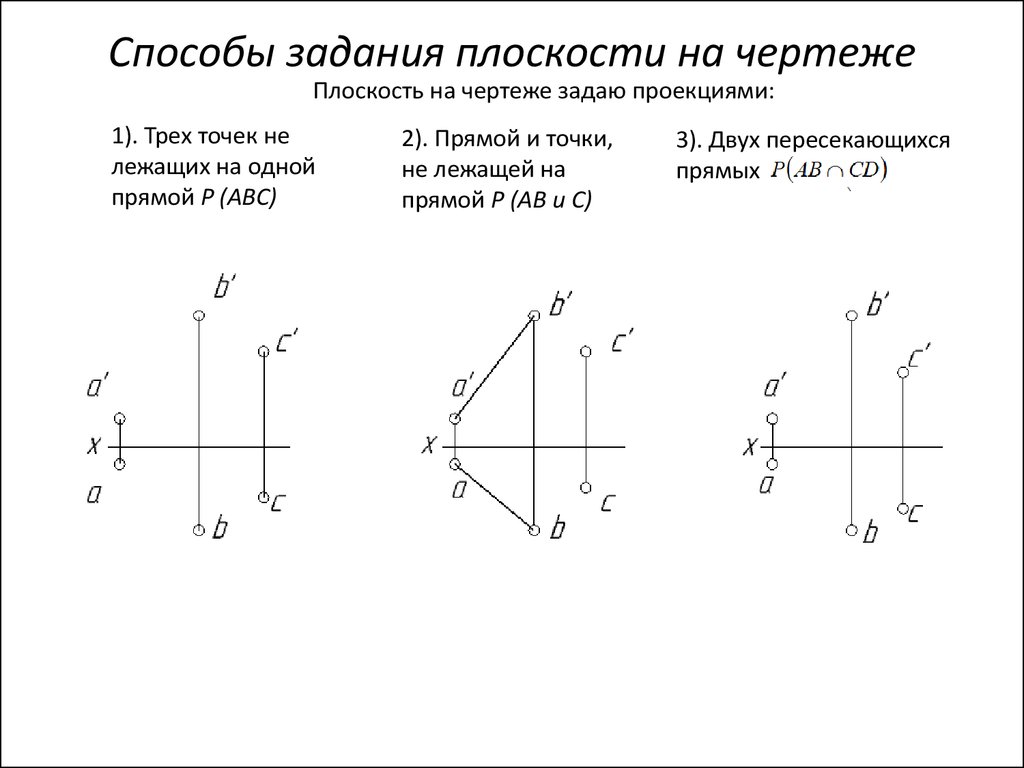
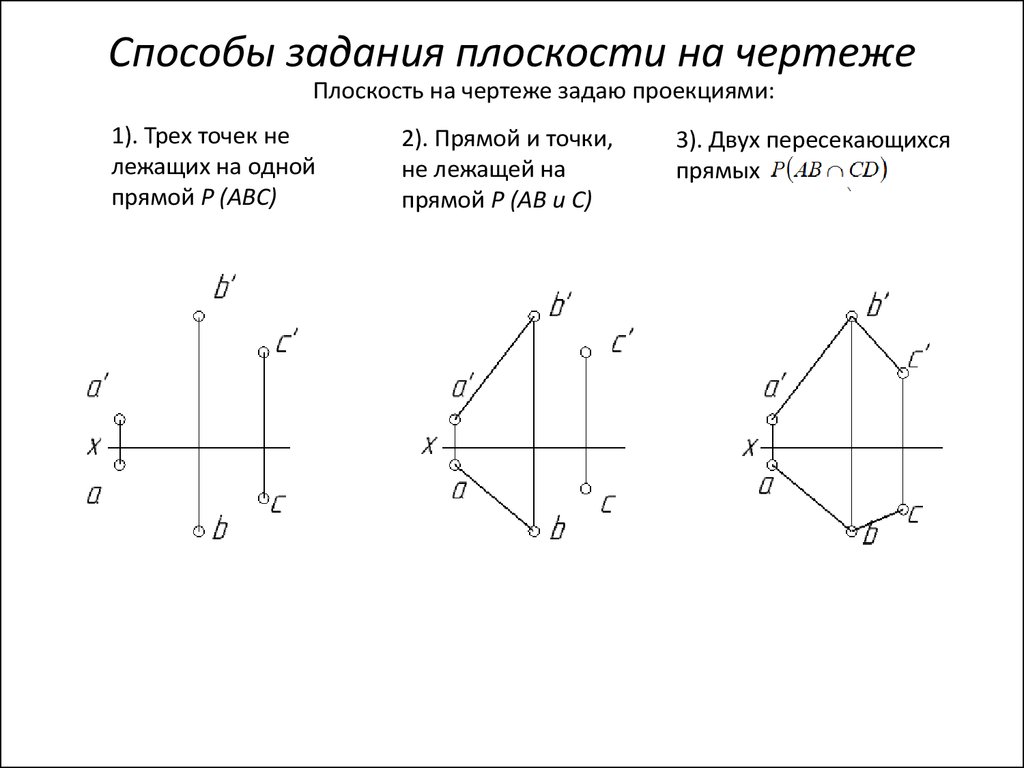
59. Способы задания плоскости на чертеже

Плоскость на чертеже задаю проекциями:
1). Трех точек не
лежащих на одной
прямой P (ABC)
2). Прямой и точки,
не лежащей на
прямой P (AB и C)
3). Двух пересекающихся
прямых

60. Способы задания плоскости на чертеже

Плоскость на чертеже задаю проекциями:
1). Трех точек не
лежащих на одной
прямой P (ABC)
2). Прямой и точки,
не лежащей на
прямой P (AB и C)
3). Двух пересекающихся
прямых

61. Способы задания плоскости на чертеже

Плоскость на чертеже задаю проекциями:
1). Трех точек не
лежащих на одной
прямой P (ABC)
2). Прямой и точки,
не лежащей на
прямой P (AB и C)
3). Двух пересекающихся
прямых

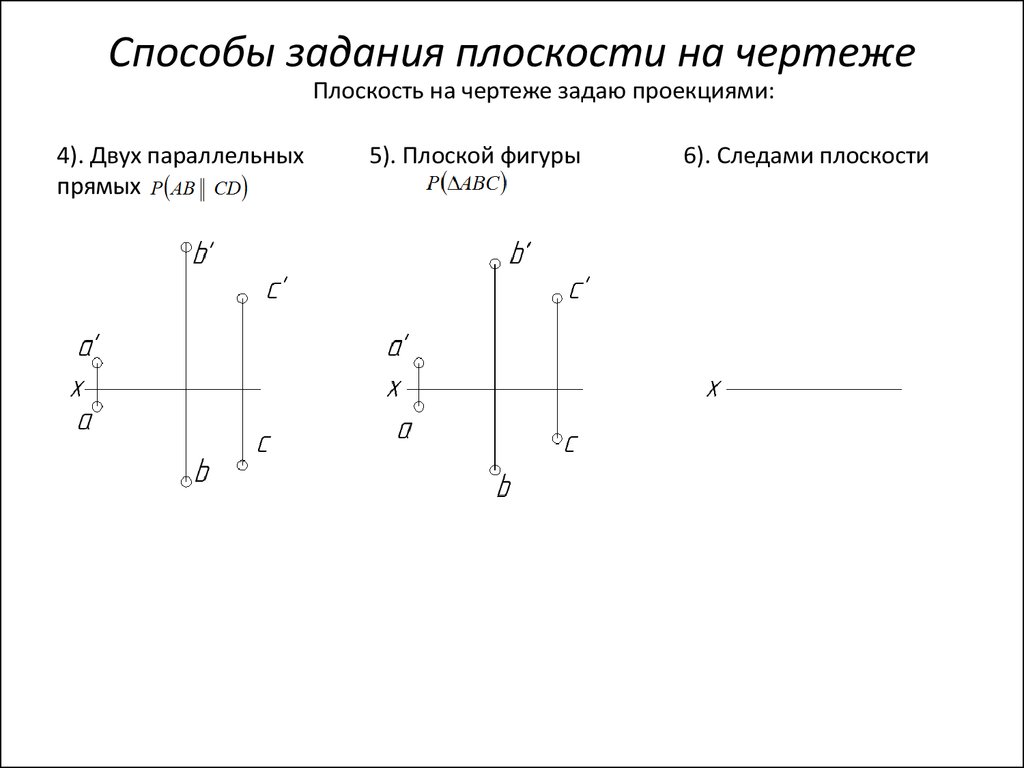
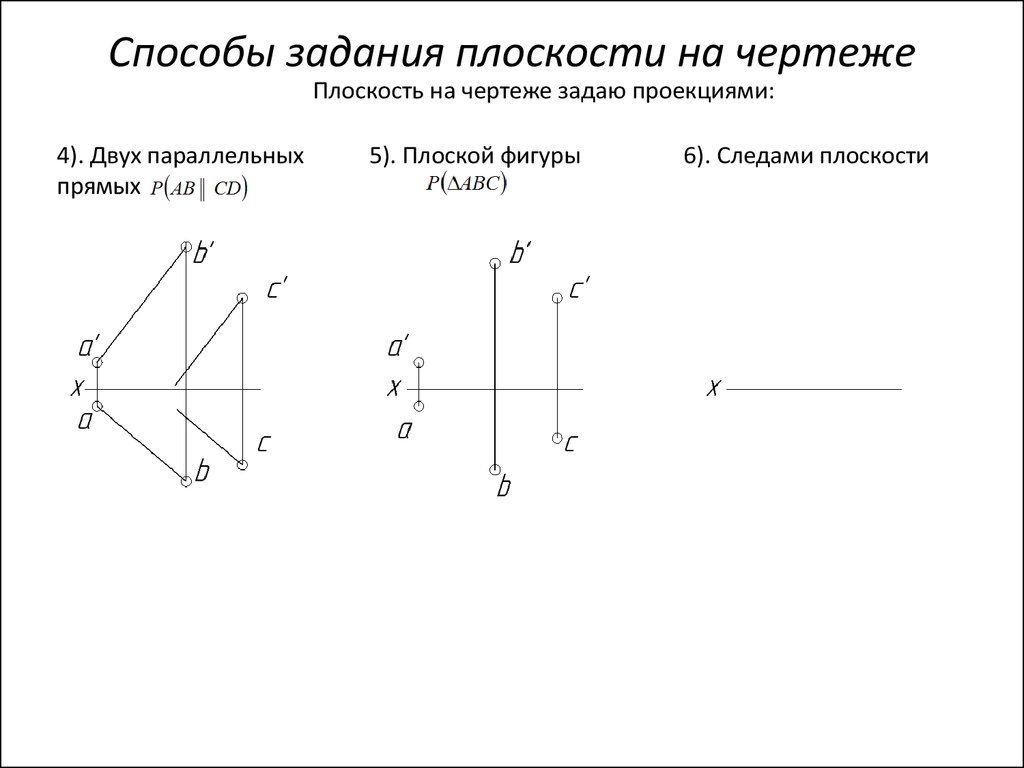
62. Способы задания плоскости на чертеже

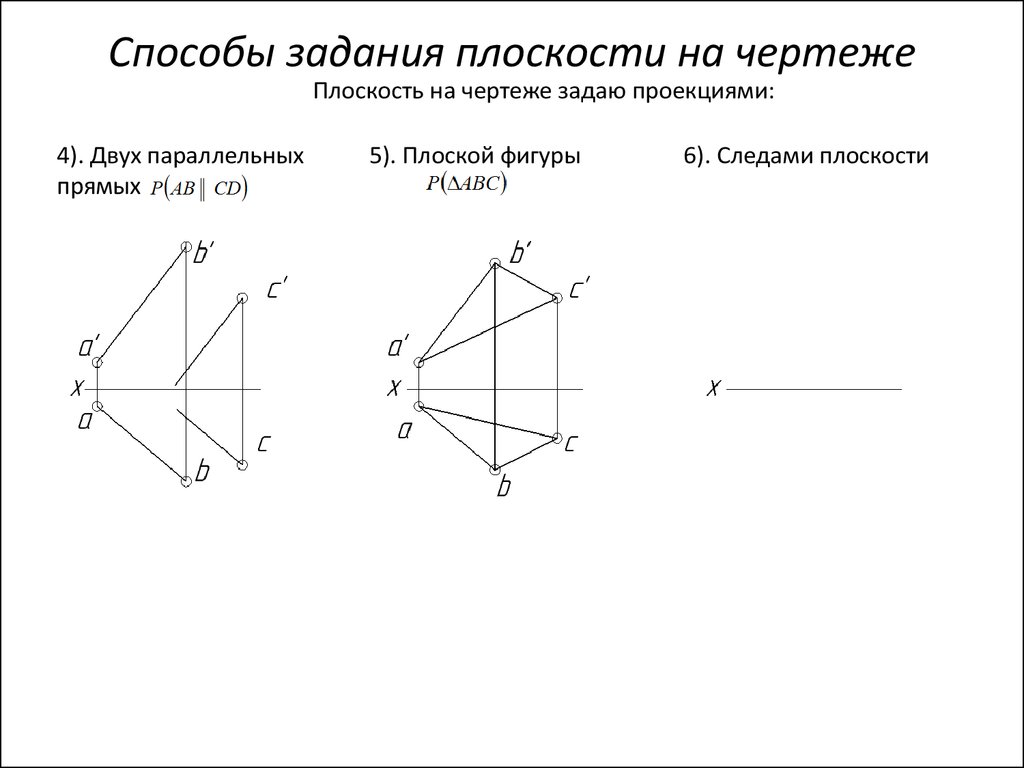
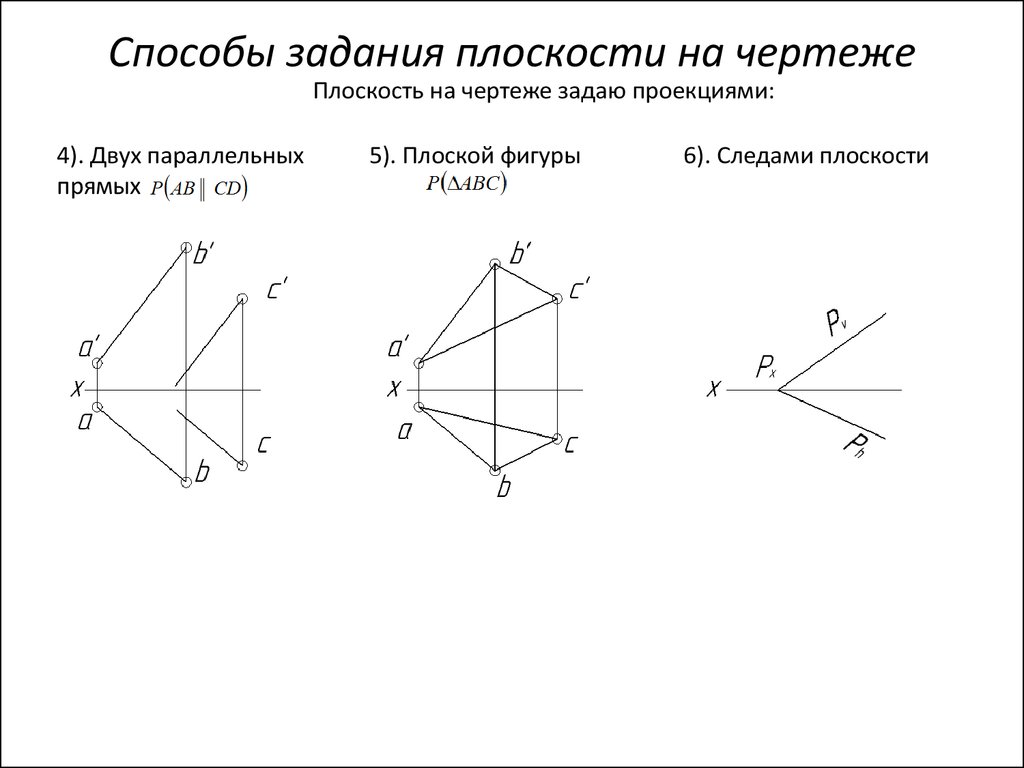
Плоскость на чертеже задаю проекциями:
4). Двух параллельных
прямых
5). Плоской фигуры
6). Следами плоскости

63. Способы задания плоскости на чертеже

Плоскость на чертеже задаю проекциями:
4). Двух параллельных
прямых
5). Плоской фигуры
6). Следами плоскости

64. Способы задания плоскости на чертеже

Плоскость на чертеже задаю проекциями:
4). Двух параллельных
прямых
5). Плоской фигуры
6). Следами плоскости

65. Способы задания плоскости на чертеже

Плоскость на чертеже задаю проекциями:
4). Двух параллельных
прямых
5). Плоской фигуры
6). Следами плоскости

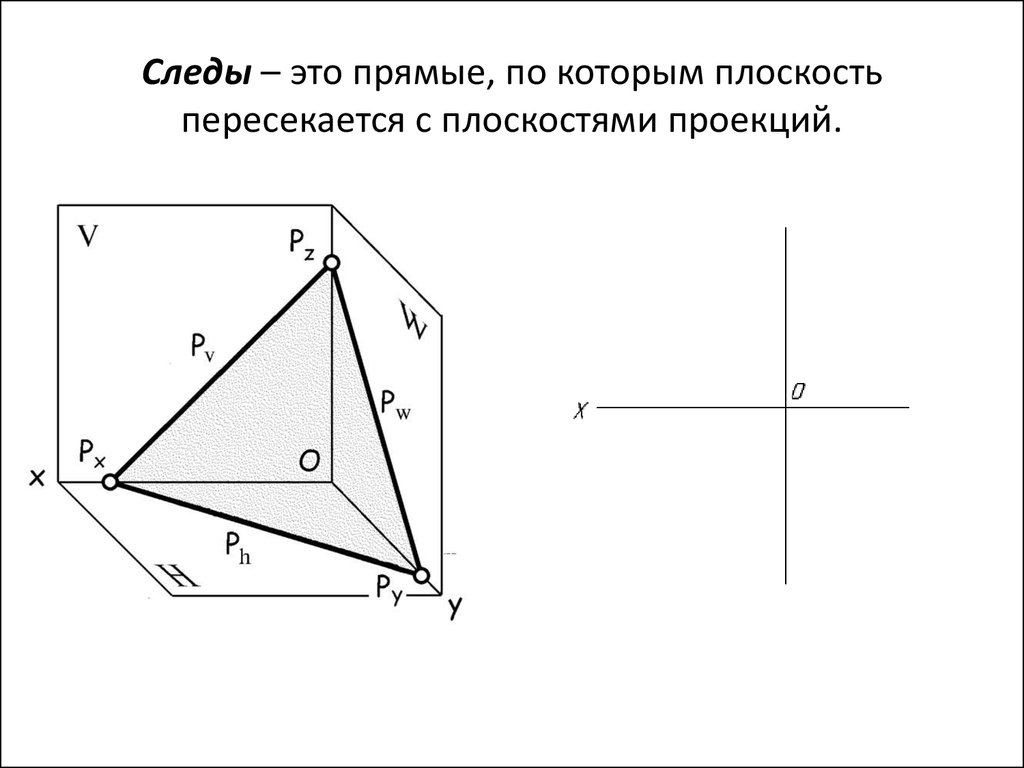
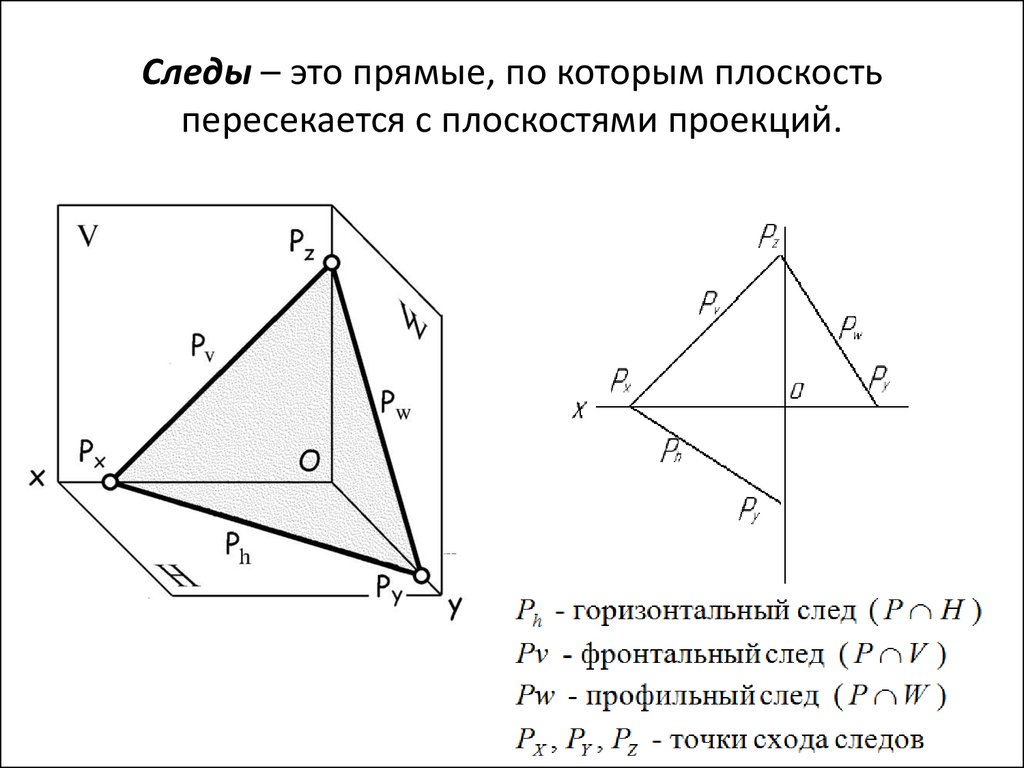
66. Следы – это прямые, по которым плоскость пересекается с плоскостями проекций.

67. Следы – это прямые, по которым плоскость пересекается с плоскостями проекций.

68.

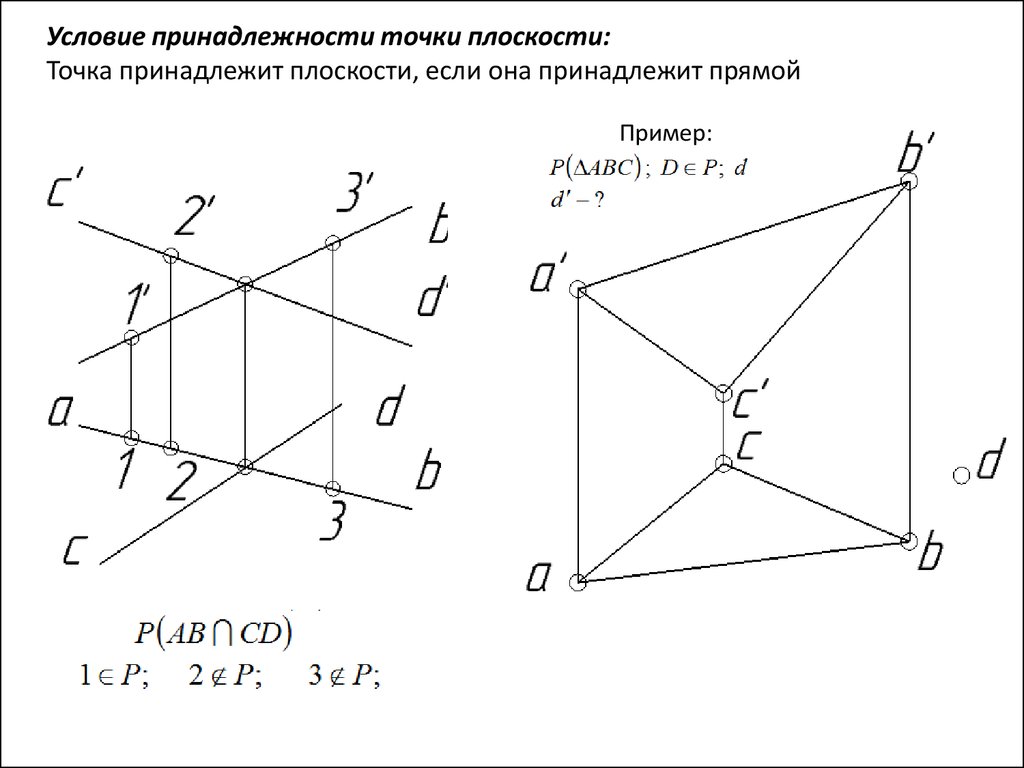
Условие принадлежности точки плоскости:
Точка принадлежит плоскости, если она принадлежит прямой
Пример:

69.

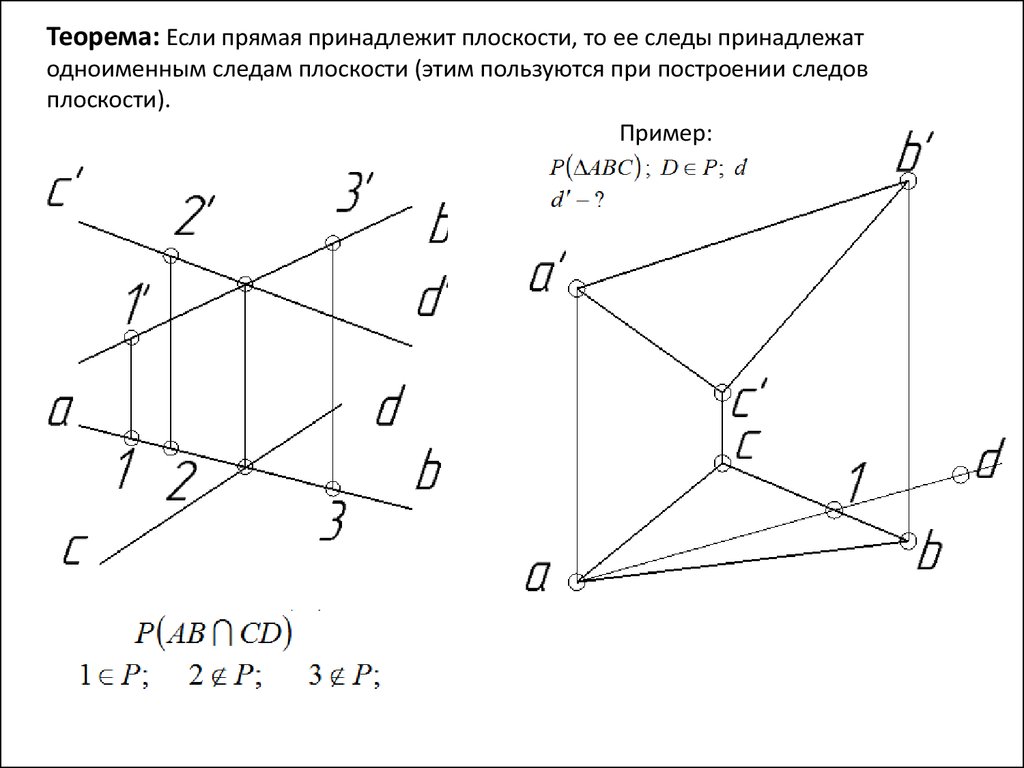
Теорема: Если прямая принадлежит плоскости, то ее следы принадлежат
одноименным следам плоскости (этим пользуются при построении следов
плоскости).
Пример:

70.

Теорема: Если прямая принадлежит плоскости, то ее следы принадлежат
одноименным следам плоскости (этим пользуются при построении следов
плоскости).
Пример:

71.

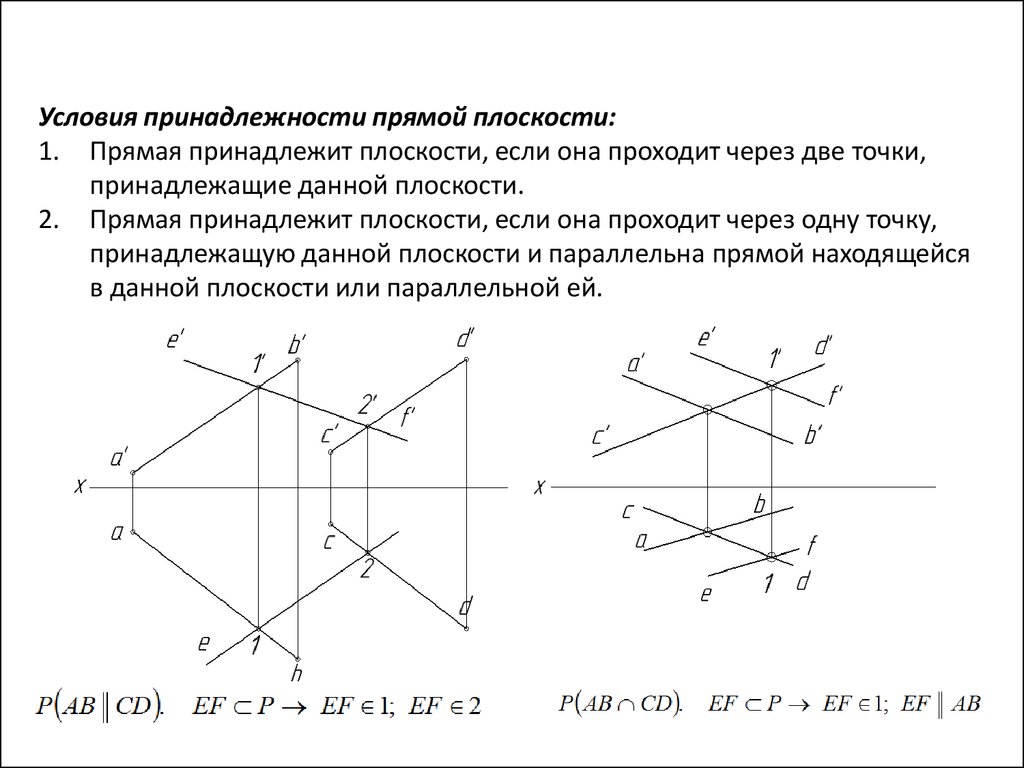
Условия принадлежности прямой плоскости:
1. Прямая принадлежит плоскости, если она проходит через две точки,
принадлежащие данной плоскости.
2. Прямая принадлежит плоскости, если она проходит через одну точку,
принадлежащую данной плоскости и параллельна прямой находящейся
в данной плоскости или параллельной ей.

72.

Условия принадлежности прямой плоскости:
1. Прямая принадлежит плоскости, если она проходит через две точки,
принадлежащие данной плоскости.
2. Прямая принадлежит плоскости, если она проходит через одну точку,
принадлежащую данной плоскости и параллельна прямой находящейся
в данной плоскости или параллельной ей.

73.

Условия принадлежности прямой плоскости:
1. Прямая принадлежит плоскости, если она проходит через две точки,
принадлежащие данной плоскости.
2. Прямая принадлежит плоскости, если она проходит через одну точку,
принадлежащую данной плоскости и параллельна прямой находящейся
в данной плоскости или параллельной ей.

74.

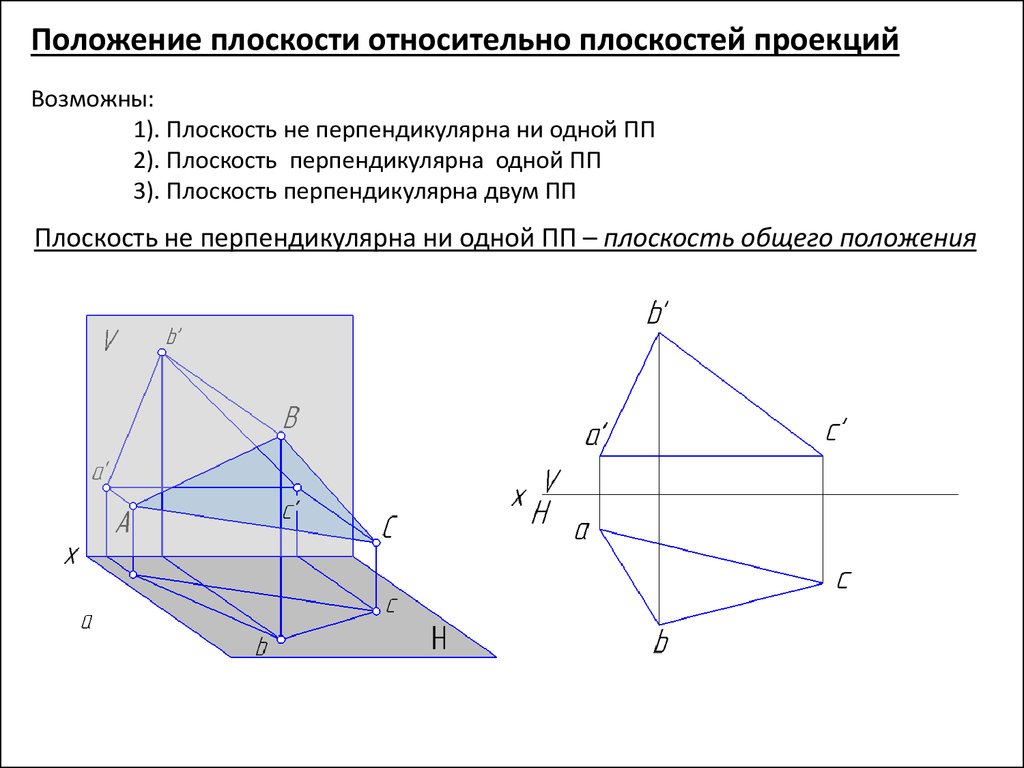
Положение плоскости относительно плоскостей проекций
Возможны:
1). Плоскость не перпендикулярна ни одной ПП
2). Плоскость перпендикулярна одной ПП
3). Плоскость перпендикулярна двум ПП
Плоскость не перпендикулярна ни одной ПП – плоскость общего положения

75.

Плоскости перпендикулярна одной или двум ПП – плоскость частного
положения
Плоскости перпендикулярна одной плоскости проекций – проецирующие плоскости
1). Горизонтально – проецирующая плоскость (ГПП) – плоскость перпендикулярная к
плоскости Н.

76.

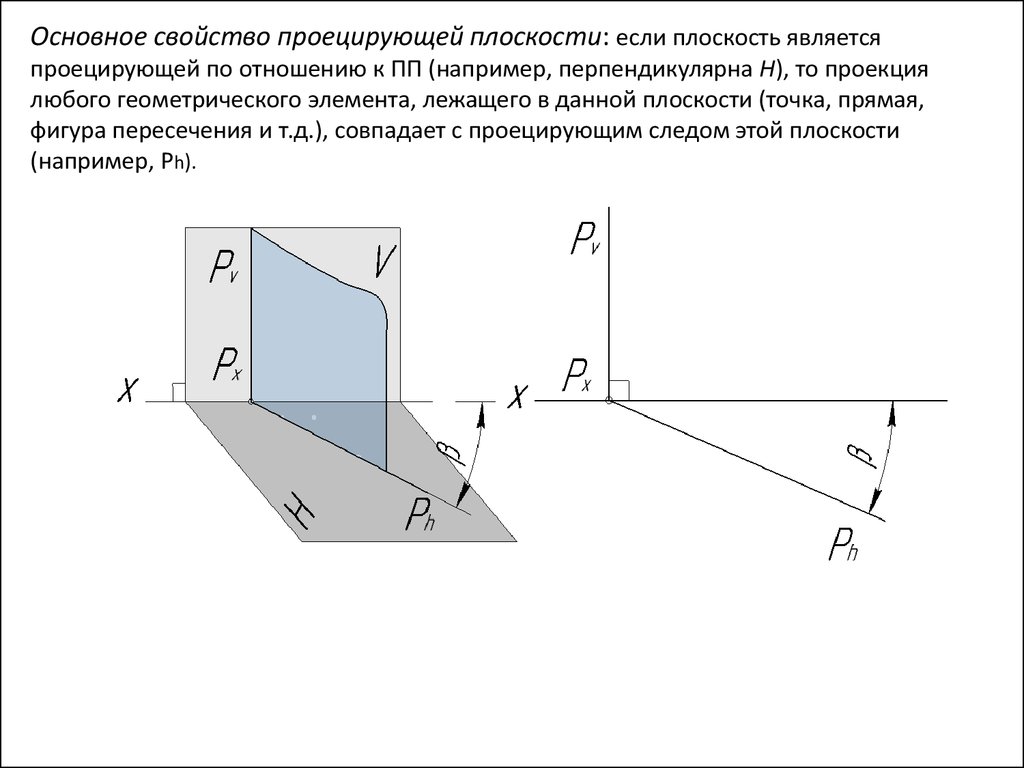
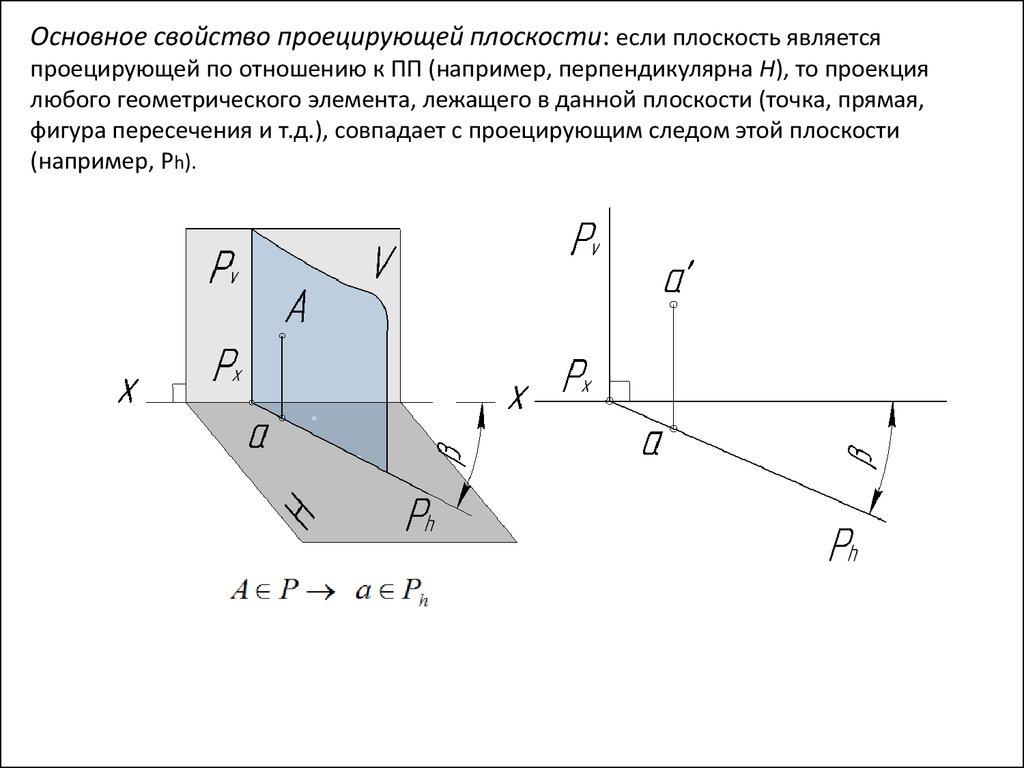
Основное свойство проецирующей плоскости: если плоскость является
проецирующей по отношению к ПП (например, перпендикулярна Н), то проекция
любого геометрического элемента, лежащего в данной плоскости (точка, прямая,
фигура пересечения и т.д.), совпадает с проецирующим следом этой плоскости
(например, Ph).

77.

Основное свойство проецирующей плоскости: если плоскость является
проецирующей по отношению к ПП (например, перпендикулярна Н), то проекция
любого геометрического элемента, лежащего в данной плоскости (точка, прямая,
фигура пересечения и т.д.), совпадает с проецирующим следом этой плоскости
(например, Ph).

78.

Основное свойство проецирующей плоскости: если плоскость является
проецирующей по отношению к ПП (например, перпендикулярна Н), то проекция
любого геометрического элемента, лежащего в данной плоскости (точка, прямая,
фигура пересечения и т.д.), совпадает с проецирующим следом этой плоскости
(например, Ph).

79.

Пример:
Построить
чертеж
фронтально-проецирующей
плоскости,
наклоненной к плоскости Н под углом 450 , задав ее точкой А и
прямой общего положения ВС.

80.

Пример:
Построить
чертеж
фронтально-проецирующей
плоскости,
наклоненной к плоскости Н под углом 450 , задав ее точкой А и
прямой общего положения ВС.

81.

Пример:
Построить
чертеж
профильно-проецирующей
плоскости,
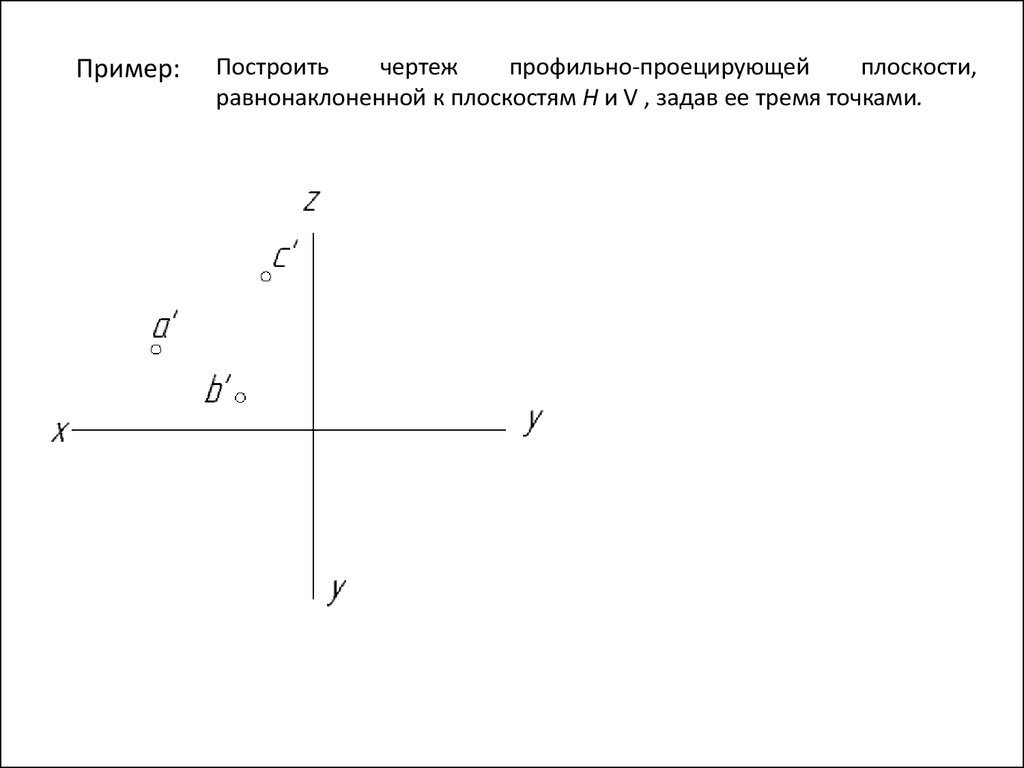
равнонаклоненной к плоскостям Н и V , задав ее тремя точками.

82.

Пример:
Построить
чертеж
профильно-проецирующей
плоскости,
равнонаклоненной к плоскостям Н и V , задав ее тремя точками.

83.

Пример:
Построить
чертеж
профильно-проецирующей
плоскости,
равнонаклоненной к плоскостям Н и V , задав ее тремя точками.

84.

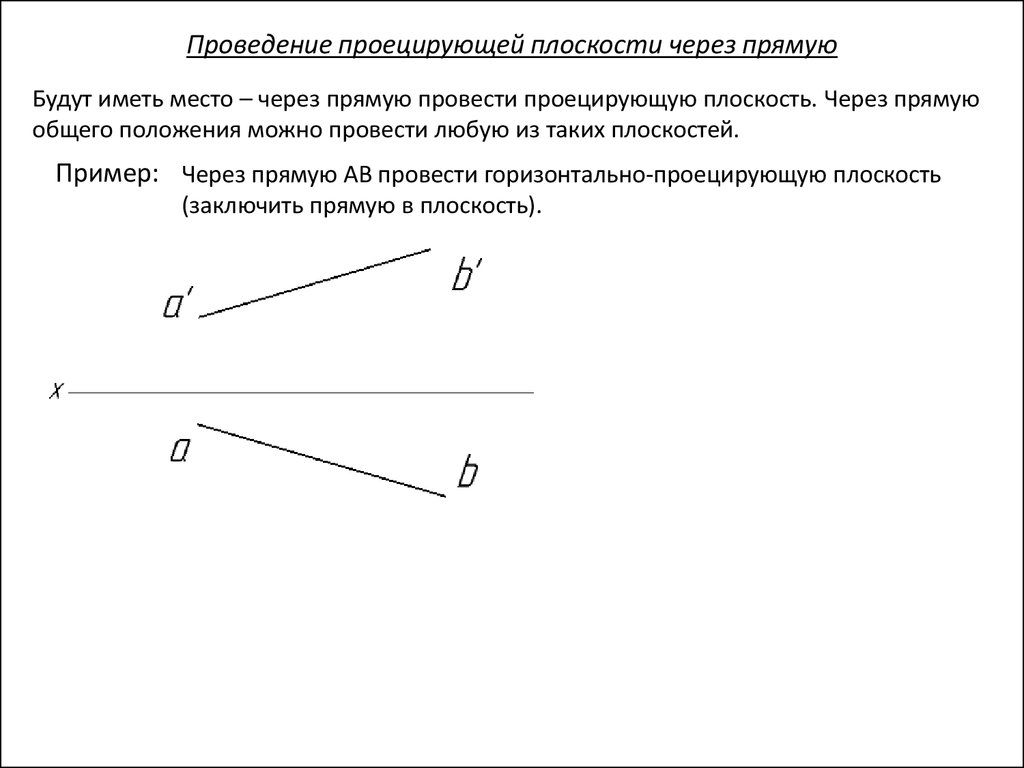
Проведение проецирующей плоскости через прямую
Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
общего положения можно провести любую из таких плоскостей.
Пример: Через прямую АВ провести горизонтально-проецирующую плоскость
(заключить прямую в плоскость).

85.

Проведение проецирующей плоскости через прямую
Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
общего положения можно провести любую из таких плоскостей.
Пример: Через прямую АВ провести горизонтально-проецирующую плоскость
(заключить прямую в плоскость).

86.

Проведение проецирующей плоскости через прямую
Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
общего положения можно провести любую из таких плоскостей.
Пример: Через прямую АВ провести фронтально-проецирующую плоскость
(заключить прямую в плоскость).

87.

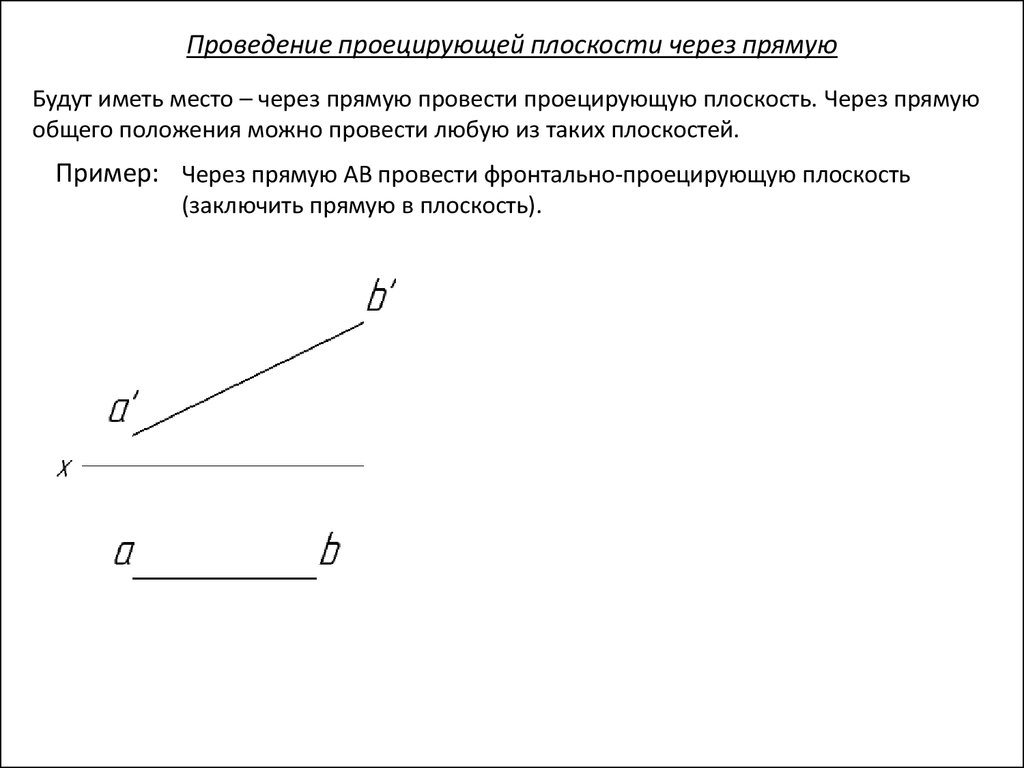
Проведение проецирующей плоскости через прямую
Будут иметь место – через прямую провести проецирующую плоскость. Через прямую
общего положения можно провести любую из таких плоскостей.
Пример: Через прямую АВ провести фронтально-проецирующую плоскость
(заключить прямую в плоскость).

88.

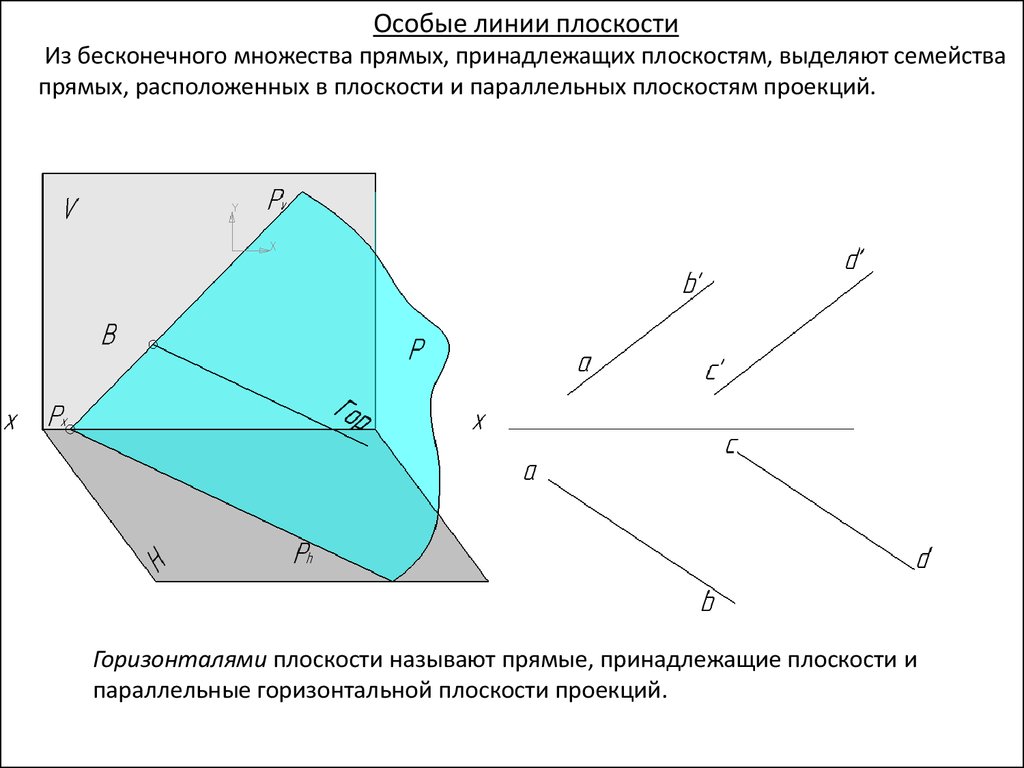
Особые линии плоскости
Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства
прямых, расположенных в плоскости и параллельных плоскостям проекций.
Горизонталями плоскости называют прямые, принадлежащие плоскости и
параллельные горизонтальной плоскости проекций.

89.

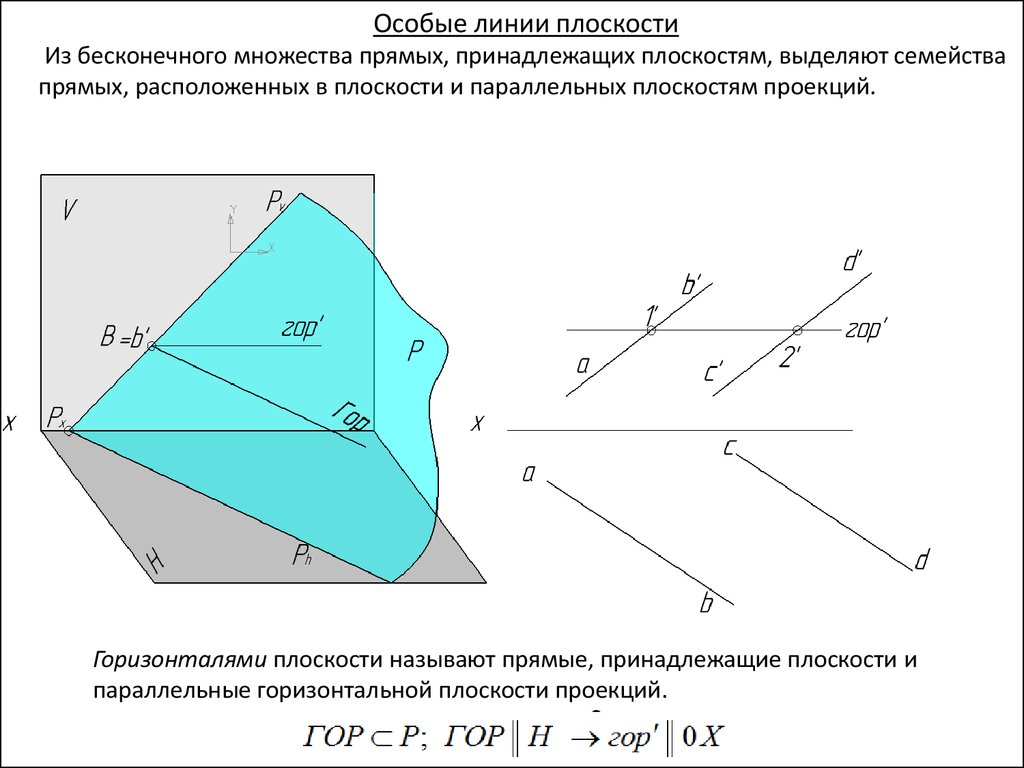
Особые линии плоскости
Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства
прямых, расположенных в плоскости и параллельных плоскостям проекций.
Горизонталями плоскости называют прямые, принадлежащие плоскости и
параллельные горизонтальной плоскости проекций.

90.

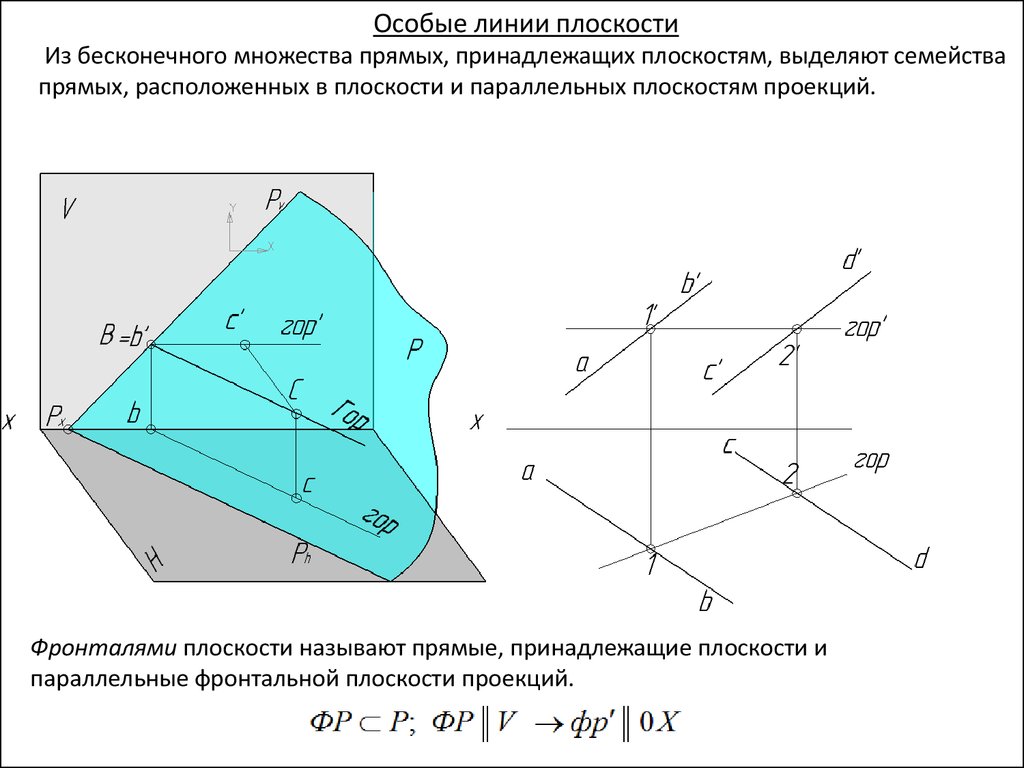
Особые линии плоскости
Из бесконечного множества прямых, принадлежащих плоскостям, выделяют семейства
прямых, расположенных в плоскости и параллельных плоскостям проекций.
Фронталями плоскости называют прямые, принадлежащие плоскости и
параллельные фронтальной плоскости проекций.