Similar presentations:
Интегральное исчисление функции. Лекция 4. Интегрирование рациональных функций
1.
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕФУНКЦИИ
ЛЕКЦИЯ 4
ИНТЕГРИРОВАНИЕ
РАЦИОНАЛЬНЫХ ФУНКЦИЙ
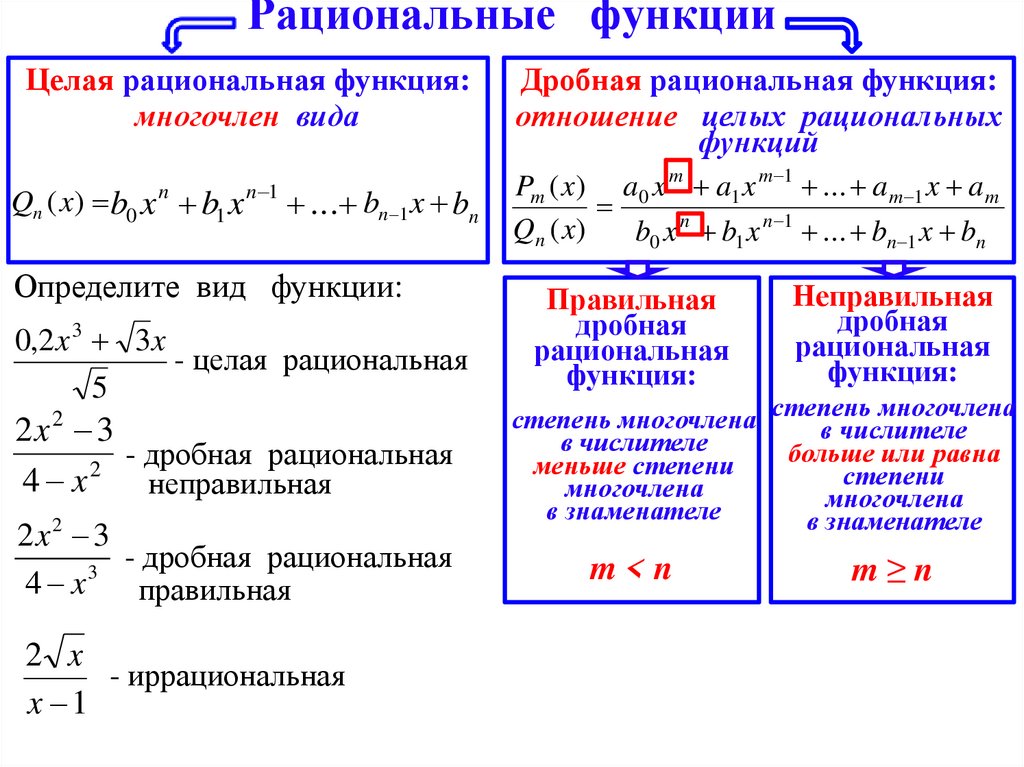
2. Рациональные функции
Целая рациональная функция:многочлен вида
Qn (x) b0 x n b1 x n 1 ... bn 1 x bn
Определите вид функции:
0,2 x 3 3x
- целая рациональная
5
2x 3
- дробная рациональная
2
4 x
неправильная
2
2x 2 3
- дробная рациональная
3
4 x
правильная
2 x
- иррациональная
x 1
Дробная рациональная функция:
отношение целых рациональных
функций
Pm ( x) a 0 x m a1 x m 1 ... a m 1 x a m
Qn ( x )
b0 x n b1 x n 1 ... bn 1 x bn
Правильная
дробная
рациональная
функция:
Неправильная
дробная
рациональная
функция:
многочлена
степень многочлена степень
в числителе
в числителе
больше или равна
меньше степени
степени
многочлена
многочлена
в знаменателе
в знаменателе
m<n
m≥n
3.
Интегрирование правильных рациональных функцийПри интегрировании правильной рациональной функции
её нужно разложить в сумму простейших рациональных функций.
Простейшими называются рациональные функции вида:
A
Ax B
Ax B
A
,
k 2, 3,...
I.
II.
, k 2, 3,... III. 2
IV. 2
k D 0,
k
ax bx c
(ax bx c)
x a ( x a)
Определите вид функции:
5
5
- не простейшая, так как
- простейшая первого вида
2
x 1 знаменатель разлагается
x 2
на
действительные
3
множители
первой
простейшая
второго
вида
степени
( x 5) 2
3x 2
- не простейшая, так как
2
3
2x 3
( x 3 ) знаменатель разлагается
- простейшая третьего вида
2
на
действительные
3x 2 x 1
множители
первой
степени
5( x 4)
- простейшая четвёртого вида
3
2
3
( x 3)
3
2
2x 9 x 9
2
- простейшая
первого вида
4.
Схема разложения правильных рациональныхфункций на простейшие рациональные функции
N/N
1
2
3
4
5
Исходная дробь
Вид ее разложения на слагаемые



 mathematics
mathematics








