Числовая окружность на координатной плоскости

1.

Тема: ТРИГОНОМЕТРИЯ
Тригонометрические
функции
Тригонометрические
преобразования
Тригонометрические
уравнения
3-й урок:
Числовая окружность на
координатной плоскости

2.

ТЕМА:
Числовая
окружность
на
координатной

3.

ЦЕЛЬ:
рассмотреть числовую окружность на
координатной плоскости; вместе найти
координаты двух точек; далее
самостоятельно составить таблицы
значений координат других основных
точек окружности;
проверить умение находить
координаты точек числовой
окружности.

4.

Актуализация знаний

5.

В курсе геометрии 9 класса изучали следующий
материал:

6.

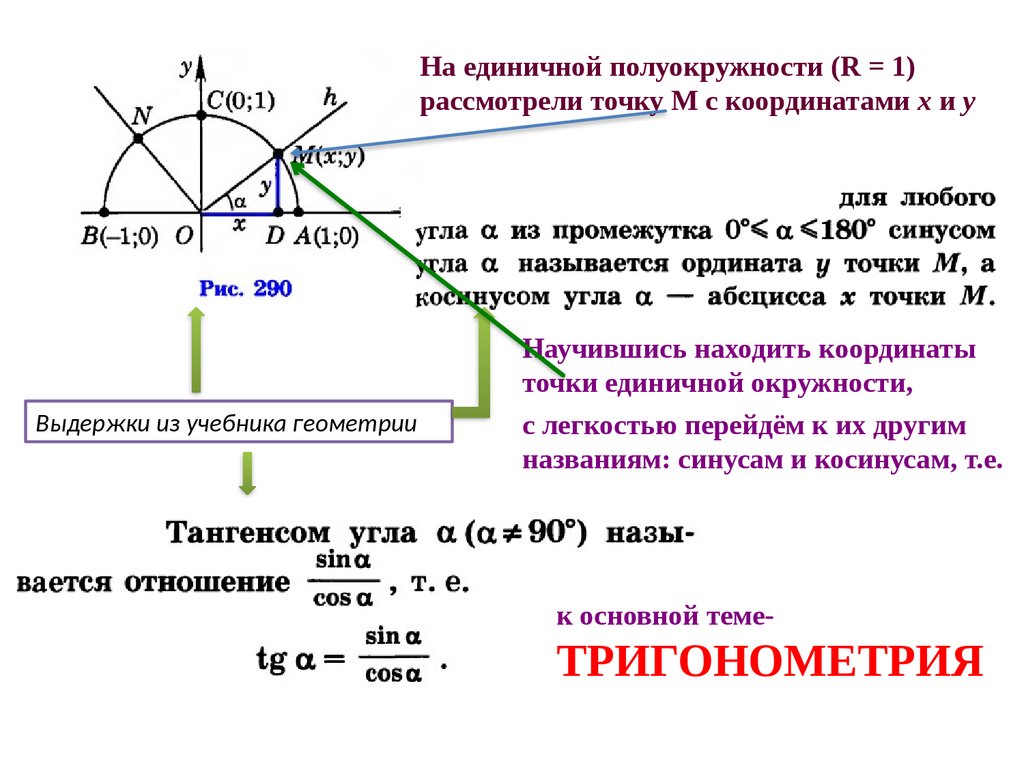
На единичной полуокружности (R = 1)
рассмотрели точку М с координатами х и у
Выдержки из учебника геометрии
Научившись находить координаты
точки единичной окружности,
с легкостью перейдём к их другим
названиям: синусам и косинусам, т.е.
к основной теме-
ТРИГОНОМЕТРИЯ

7.

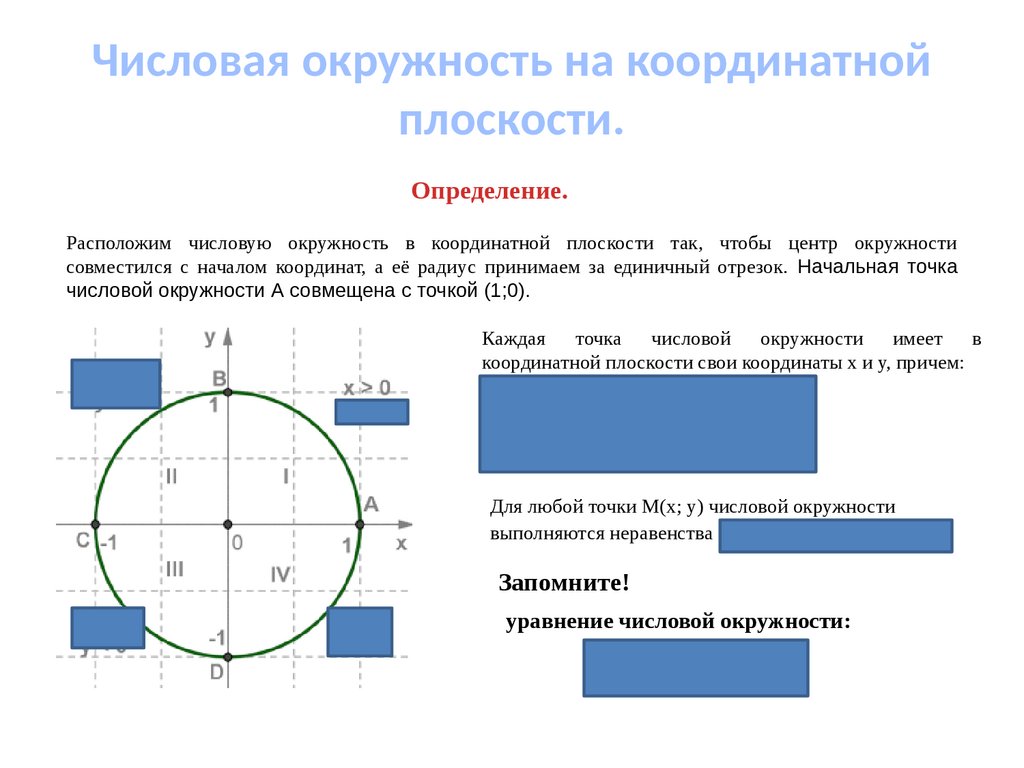
Числовая окружность на координатной
плоскости.
Определение.
Расположим числовую окружность в координатной плоскости так, чтобы центр окружности
совместился с началом координат, а её радиус принимаем за единичный отрезок. Начальная точка
числовой окружности A совмещена с точкой (1;0).
Каждая точка числовой окружности имеет в
координатной плоскости свои координаты х и у, причем:
1) x > 0, у > 0 в первой четверти;
2) х < 0, у > 0 во второй четверти;
3) х < 0, у < 0 в третьей четверти;
4) х > 0, у < 0 в четвертой четверти.
Для любой точки М(х; у) числовой окружности
выполняются неравенства -1 < x < 1; -1 < у < 1.
Запомните!
уравнение числовой окружности:

8.

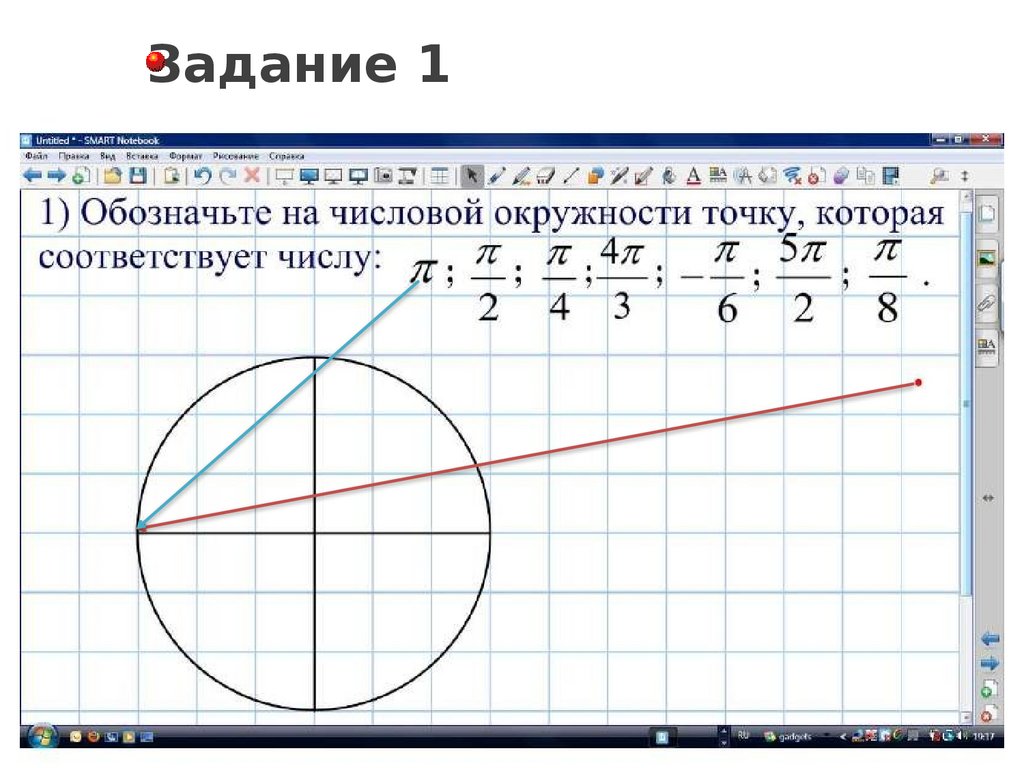
Задание 1

9.

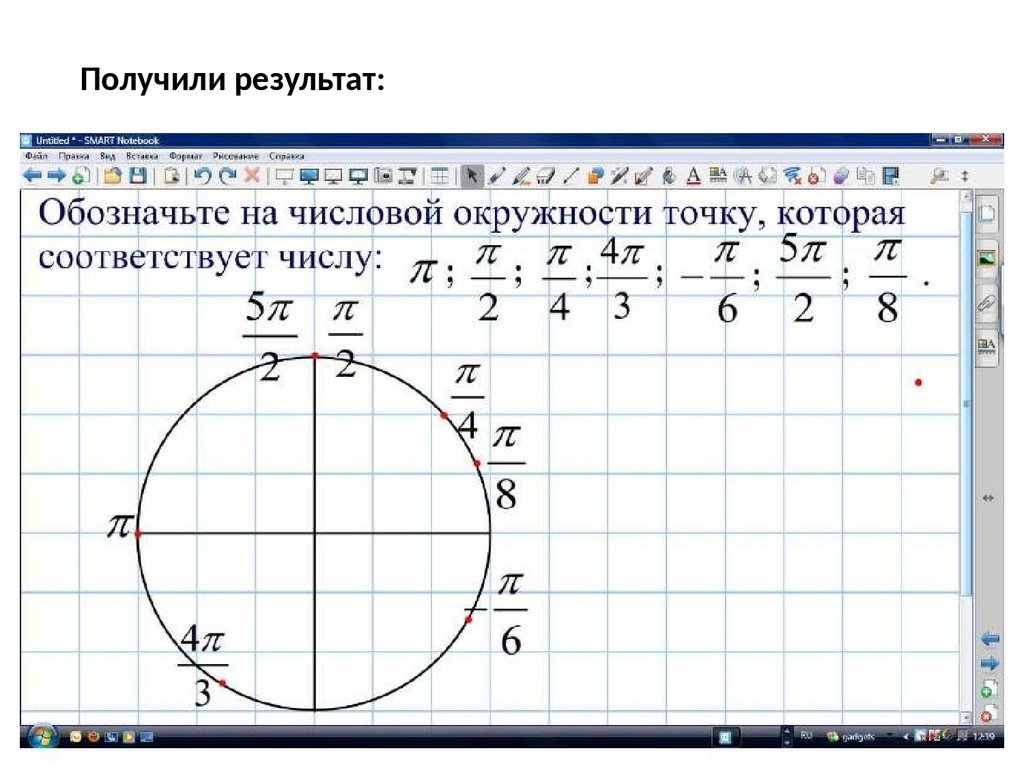
Получили результат:

10.

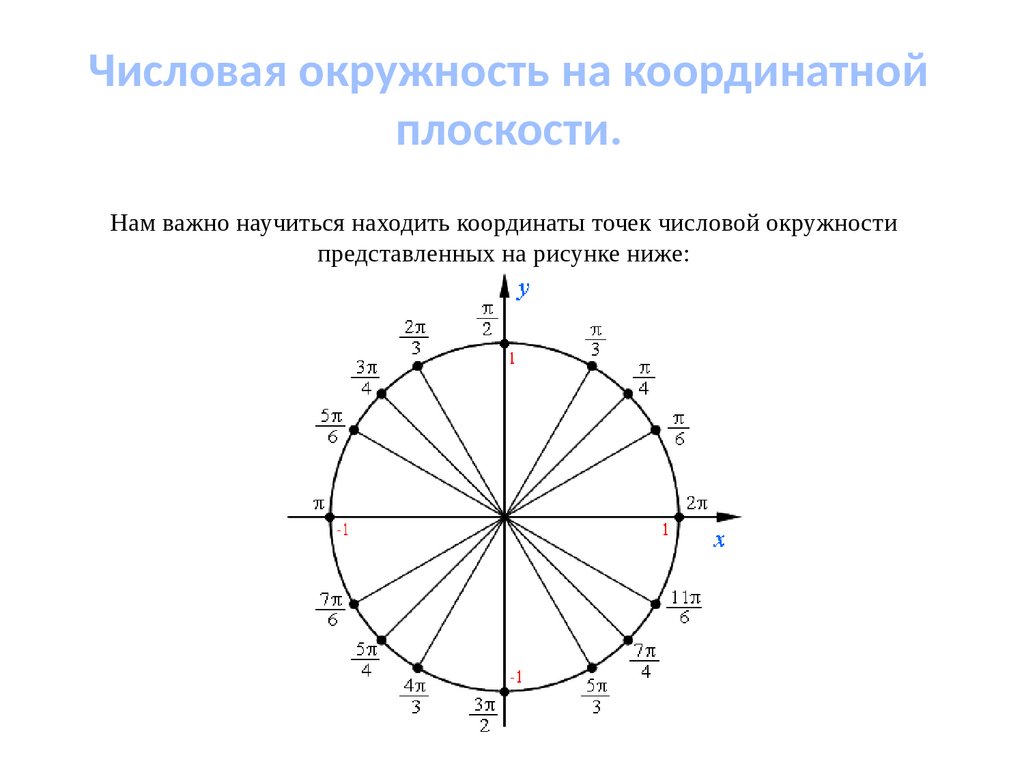
Числовая окружность на координатной
плоскости.
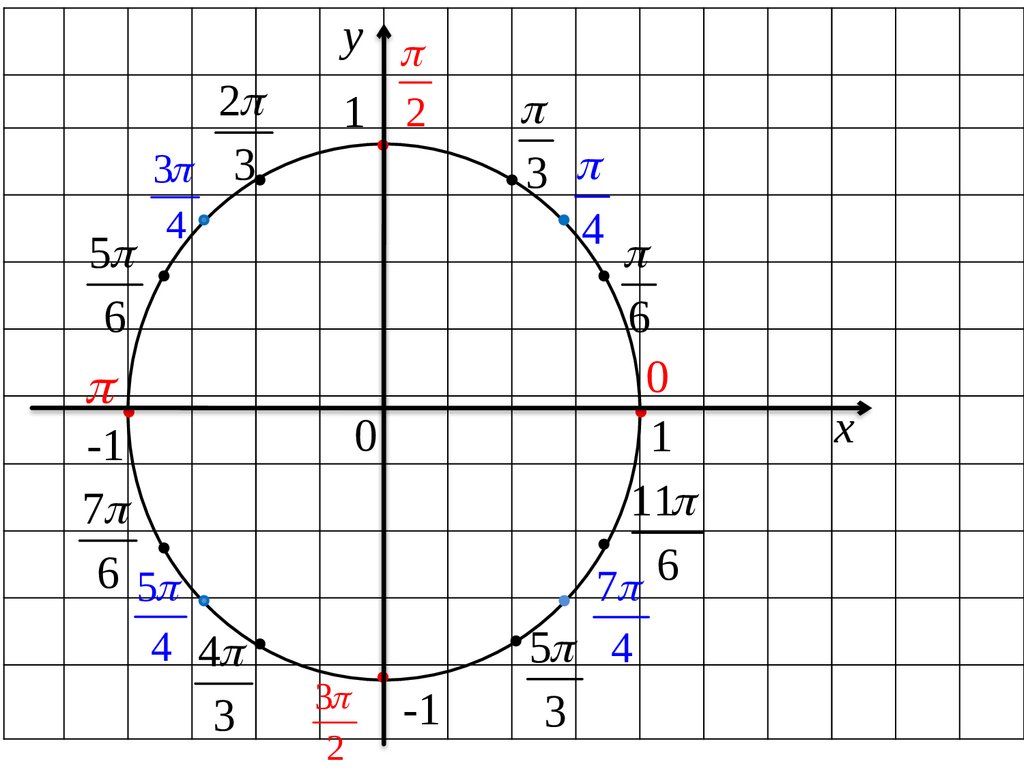
Нам важно научиться находить координаты точек числовой окружности
представленных на рисунке ниже:

11.

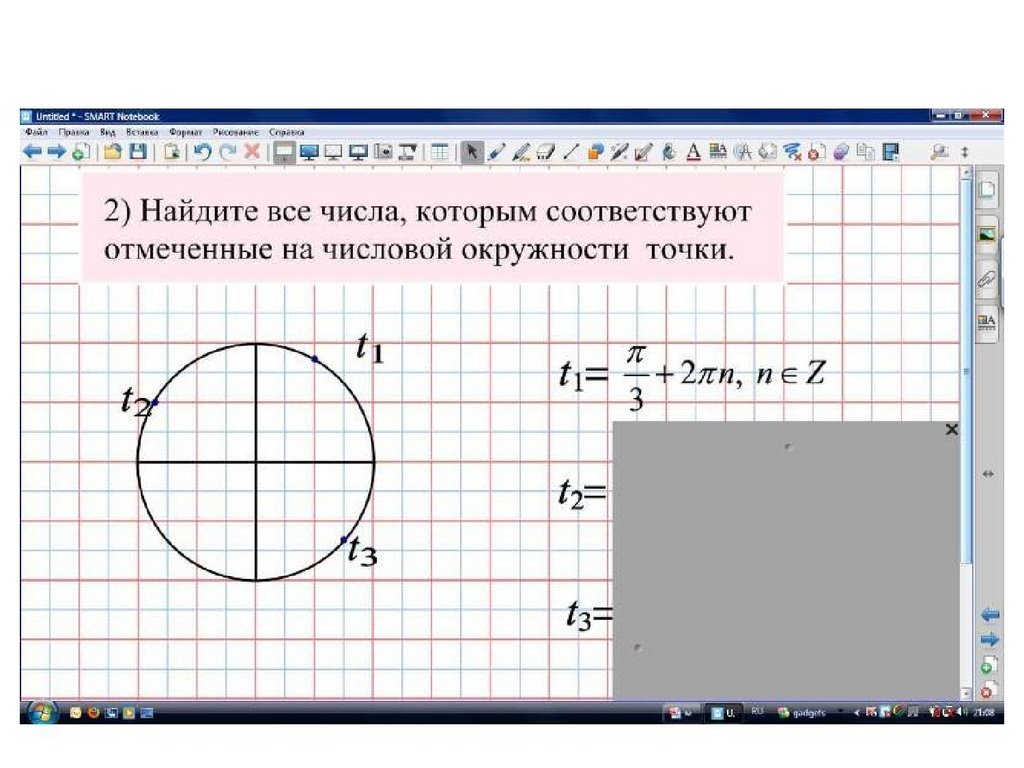
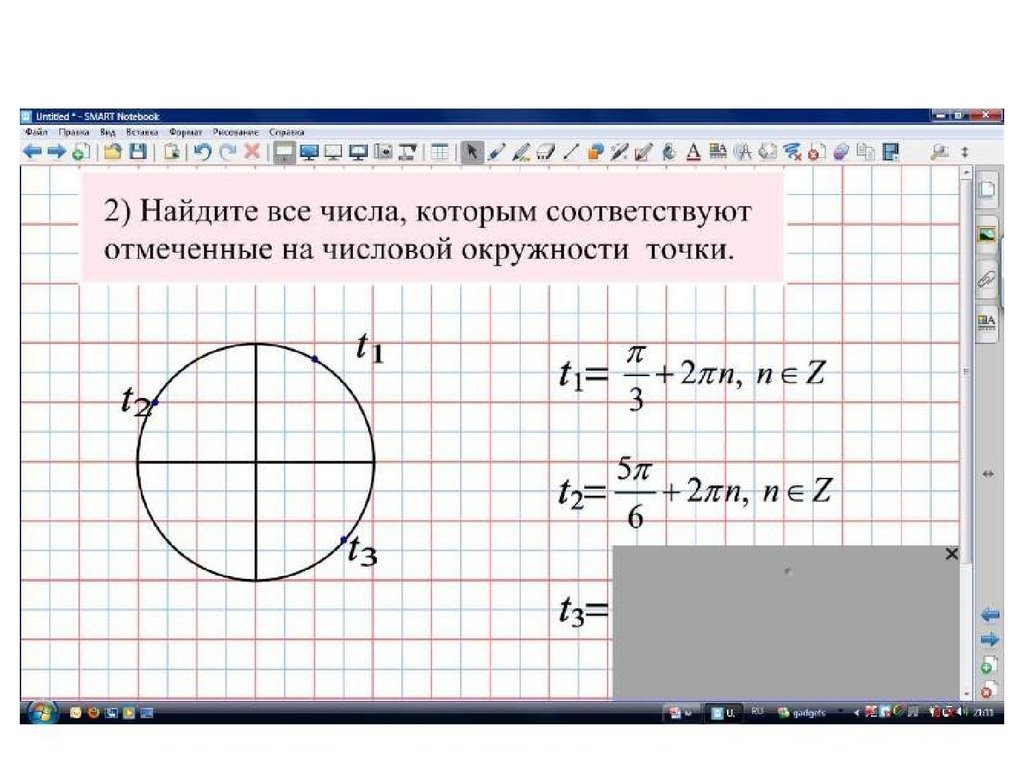
Задание 2

12.

13.

14.

Итог выполнения задания:

15.

Изучение нового материала

16.

Учитель
Возьмём систему координат и на неё
наложим числовую окружность так,
чтобы их центры совпали, а
горизонтальный радиус окружности
совпал с положительным направлением
оси ОХ

17.

2
3 3
5
6
у
1 2
4
6
0
1
11
6
7
0
-1
7
6 5
4 4
3
3
2
3
4
-1
5 4
3
х

18.

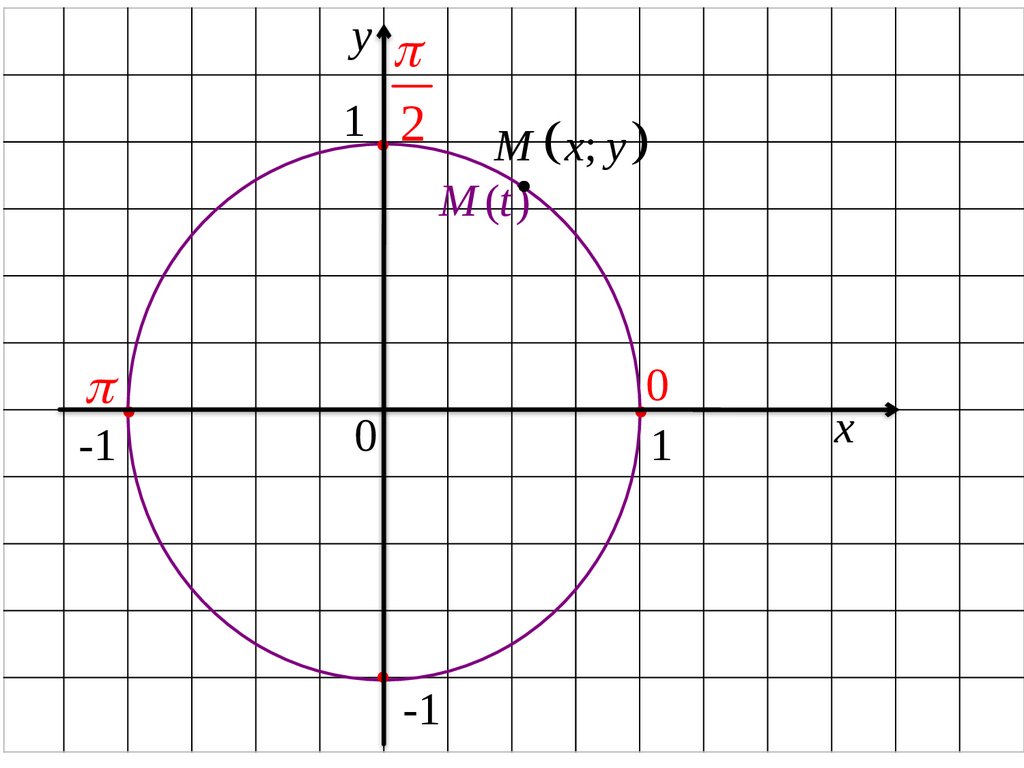
Учитель
В результате имеем точки, которые
принадлежат одновременно числовой
окружности и координатной
плоскости. Рассмотрим одну из таких
точек, например, точку М

19.

у
1 2
-1
M x; y
М (t )
0
1
0
-1
х

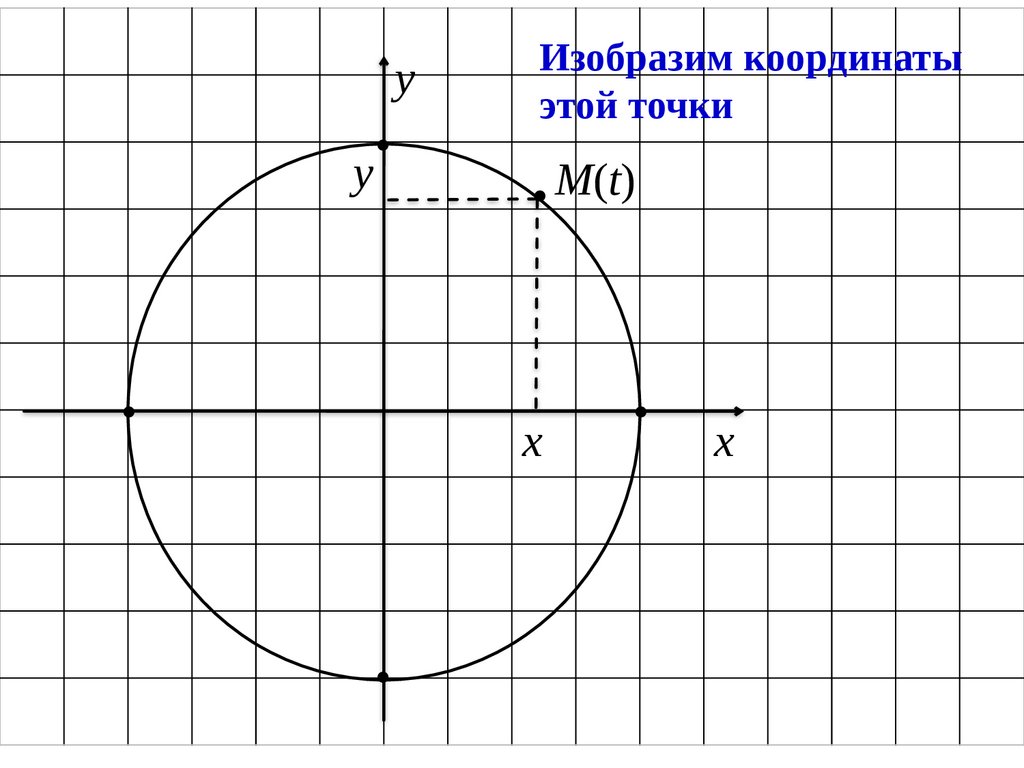
20.

у
Изобразим координаты
этой точки
у
М(t)
х
х

21.

Учитель
Найдем координаты интересующих нас
точек единичной окружности, которые
рассмотрели ранее со знаменателями 4,
3 , 6 и числителем π.

22.

Задание 3
Найти координаты точки единичной
окружности, соответствующей числу,
соответственно, и углу
4

23.

Изобразим
радиус
и по
координаты
точки
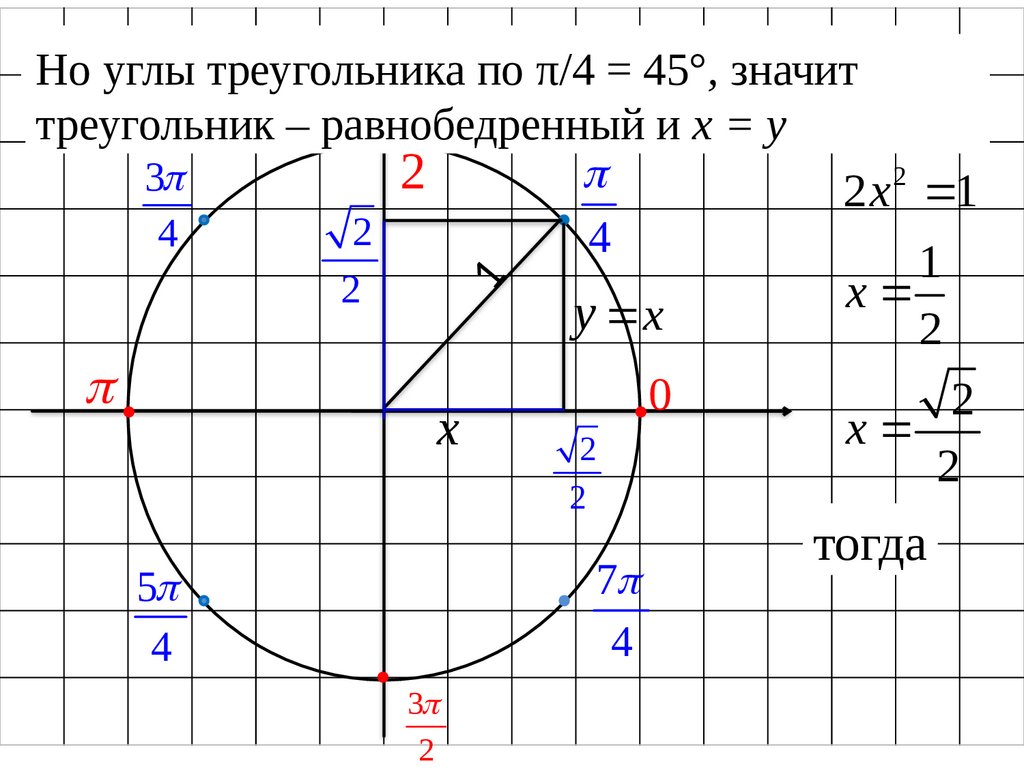
НоПоуглы
треугольника
π/4 = х45°,
значит
теореме
Пифагора
имеем
+
х
=
1
4
треугольник – равнобедренный и х = у
2
2
3
2 х 1
2
4
4
1
2
х
у х
2
0
2
х
х
2
2
2
2
1
2
2
7
4
5
4
3
2
тогда

24.

Задание 4
Найти координаты точки единичной
окружности, соответствующей числам
(углам)
6
и 3

25.

5
6
7
6
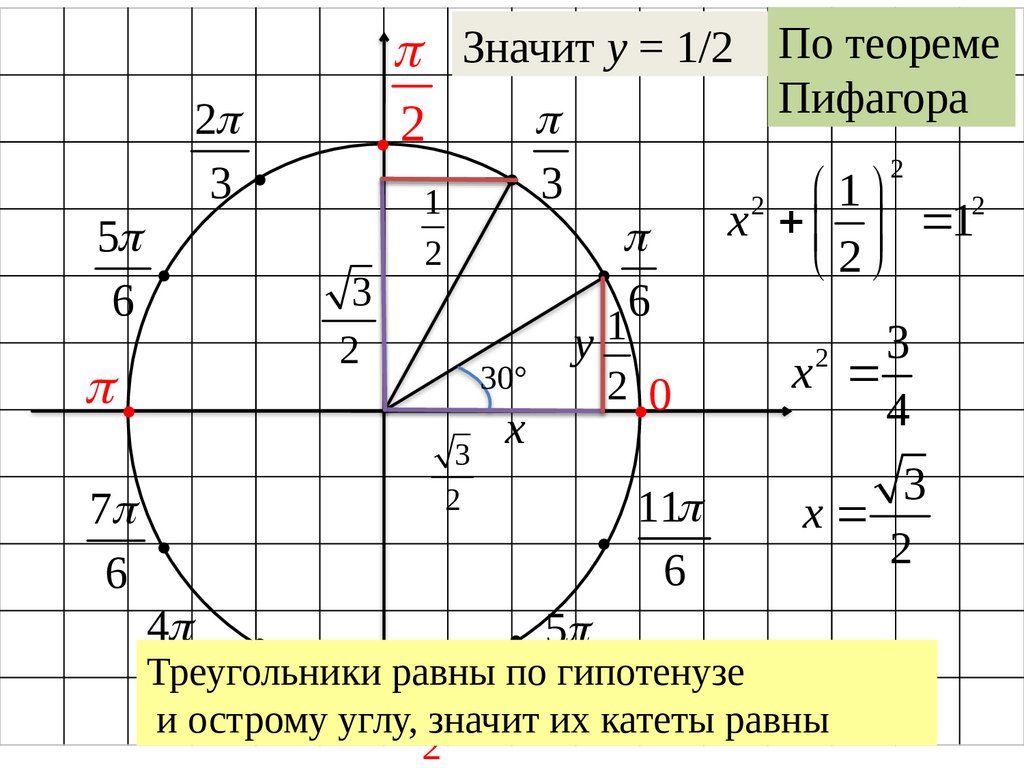
Значит у = 1/2 По теореме
Пифагора
2
2
3
3
2
3
1
2
30°
3
2
х
2
6
1
2
х 1
2
у1
2 0
11
6
4
5
Треугольники равны
3 по гипотенузе
3
3
2
3
х
4
2
3
х
2
и острому углу, значит их катеты равны
2

26.

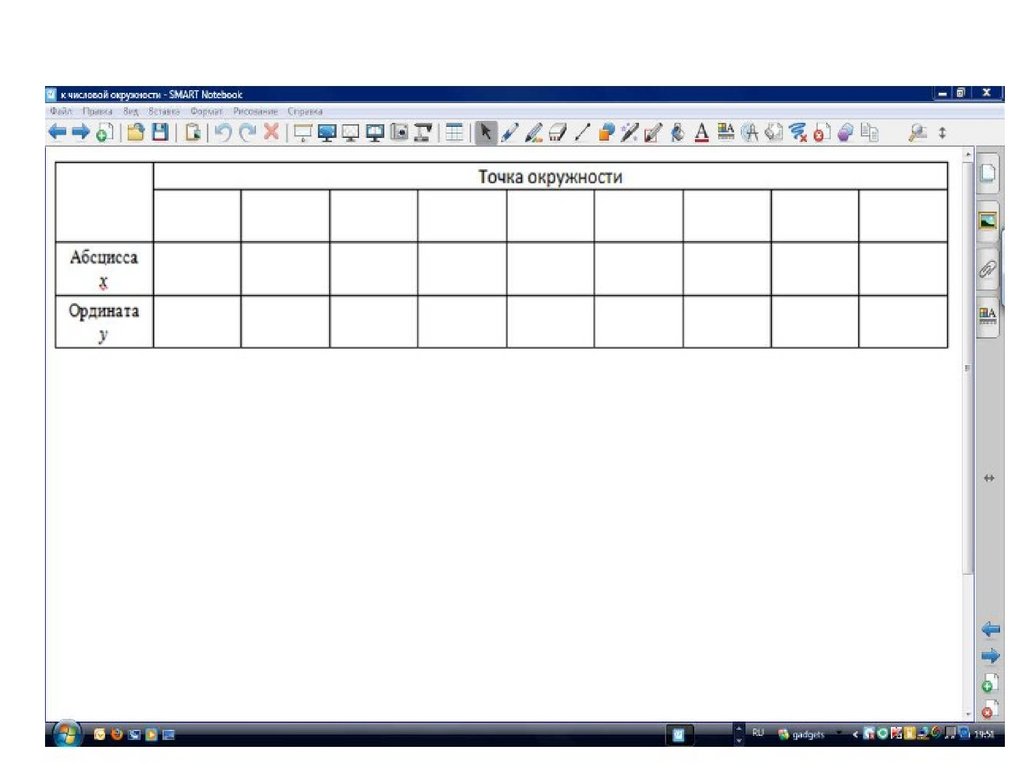
Задание 5
Заполнить первую таблицу .

27.

28.

Учитель
Сначала в таблицу внести точки
окружности, кратные 2 и 4

29.

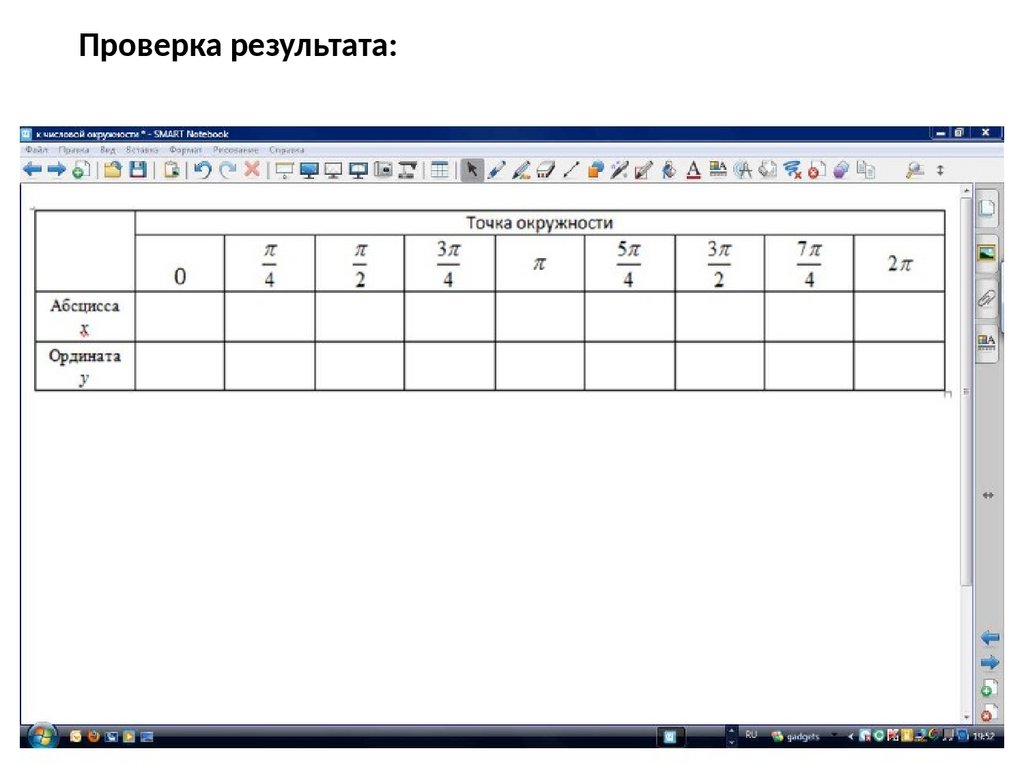
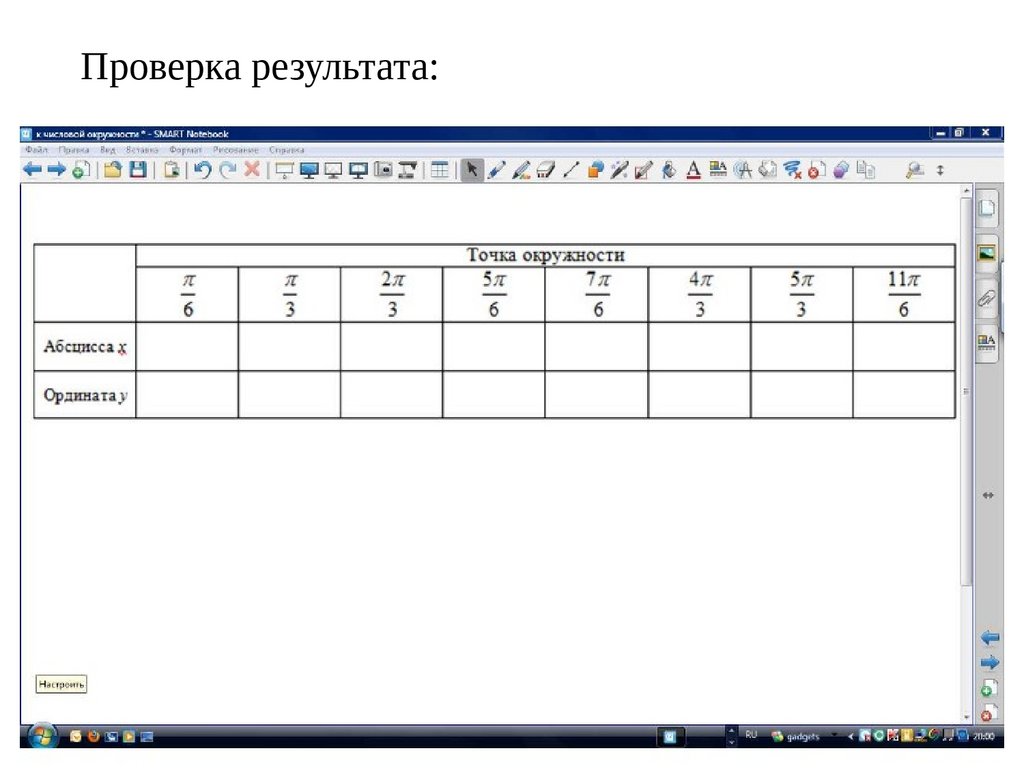
Проверка результата:

30.

Задание 6
Заполнить самостоятельно в таблице
ординаты и абсциссы данных точек с
учётом знаков координат, в
зависимости от того, в какой
четверти расположена точка,
используя выше полученные длины
отрезков для координат точек.

31.

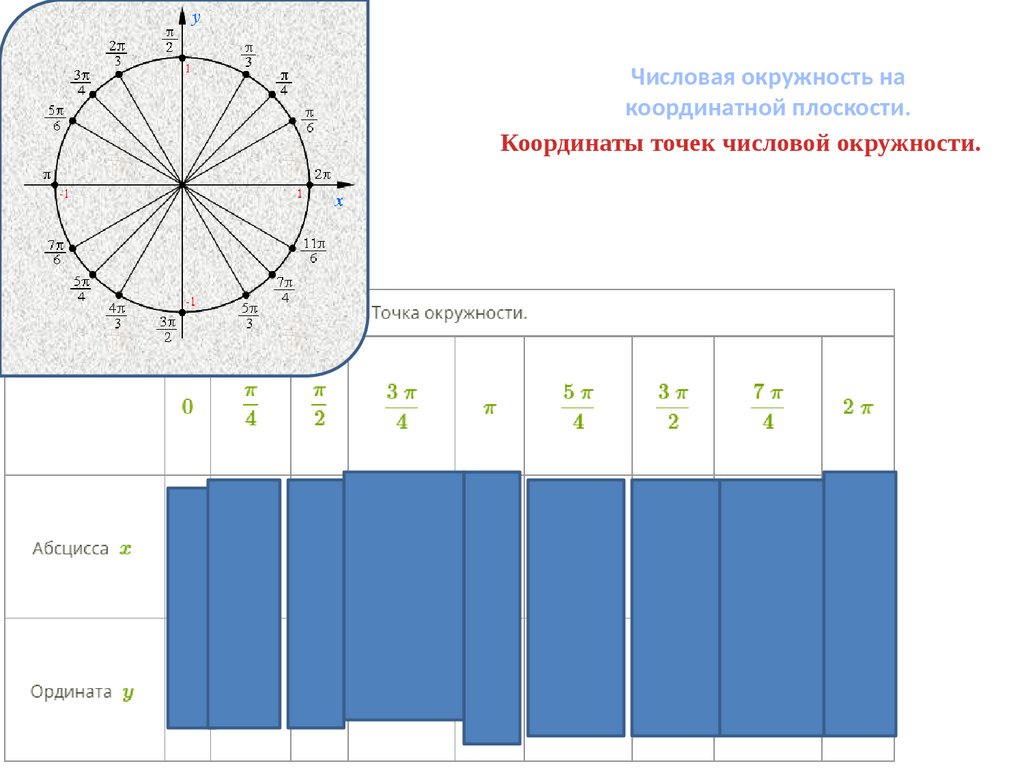
Числовая окружность на
координатной плоскости.
Координаты точек числовой окружности.

32.

Задание 7
Заполнить вторую таблицу .

33.

34.

Учитель
Сначала в таблицу внести точки
окружности, кратные 3 и 6

35.

Проверка результата:

36.

Задание 8
Заполнить самостоятельно в
таблице ординаты и абсциссы
данных точек

37.

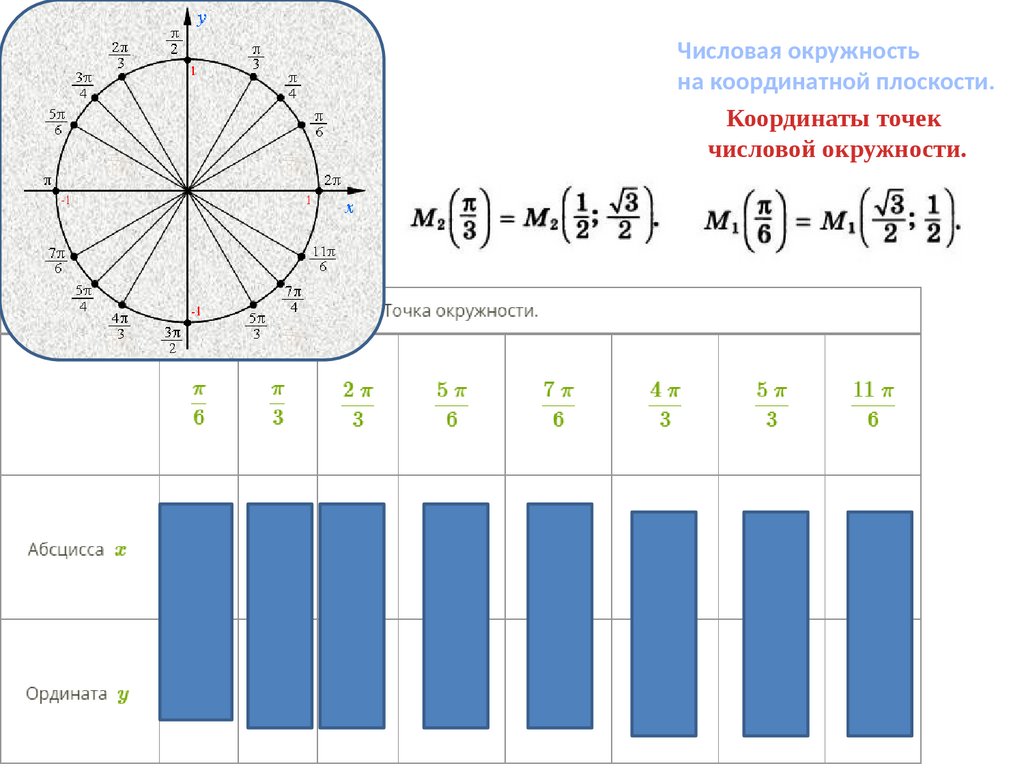
Числовая окружность
на координатной плоскости.
Координаты точек
числовой окружности.

38.

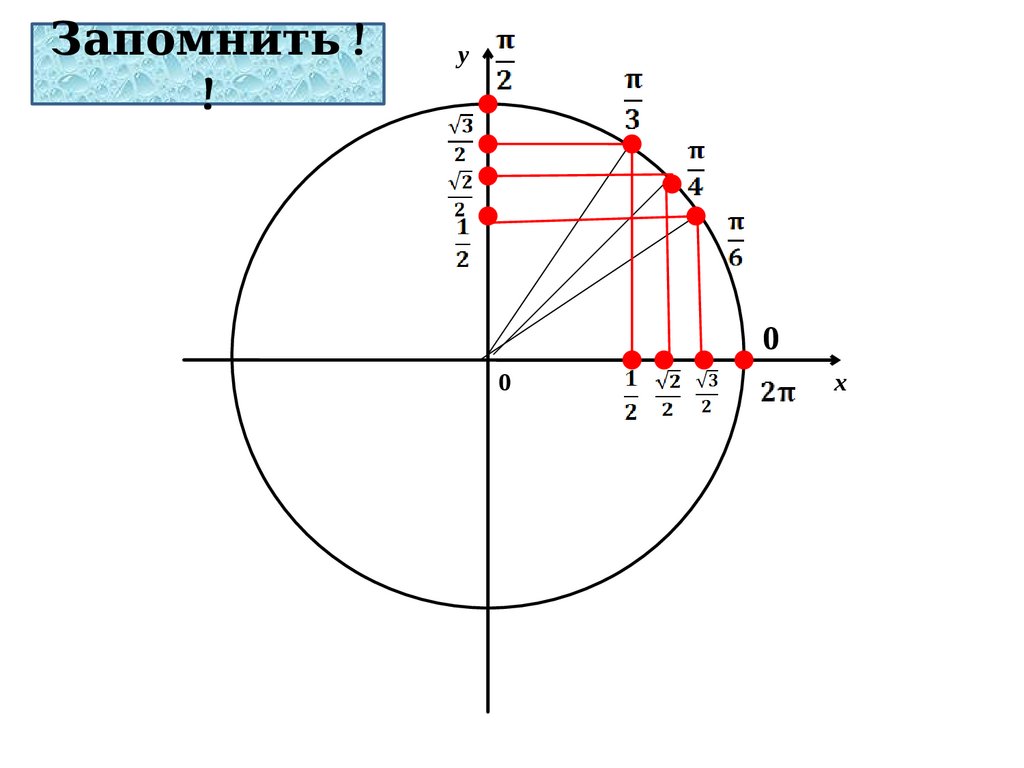
Запомнить !
!
у
0
0
х

39.

Числовая окружность на координатной
плоскости.
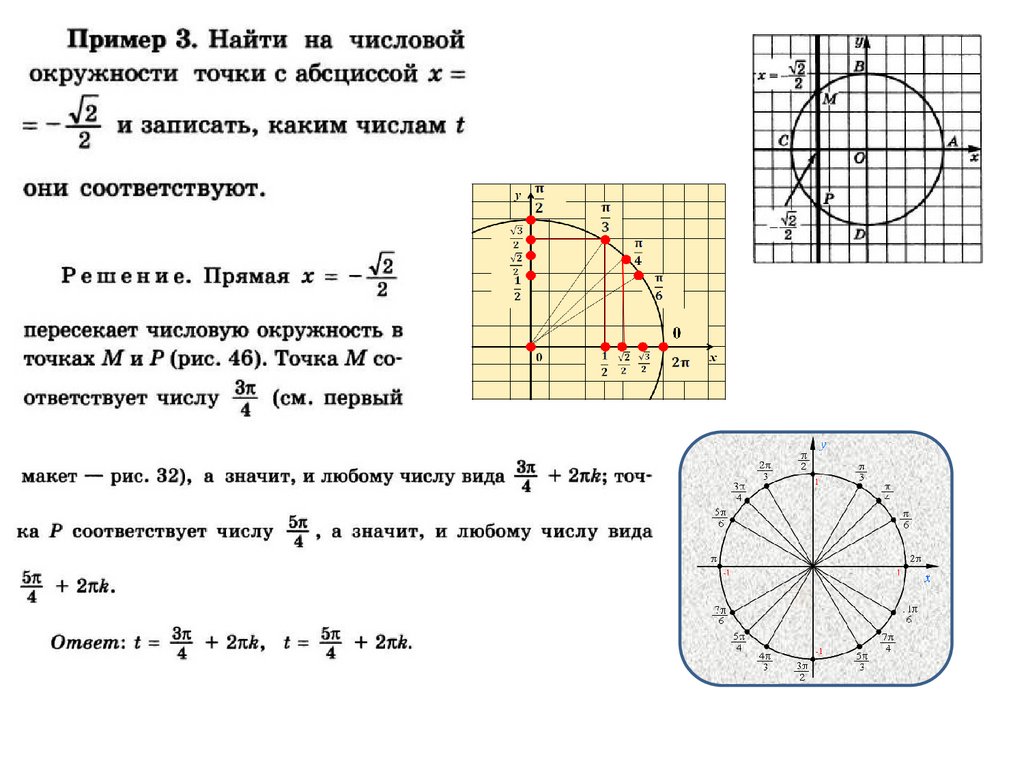
Пример
Найти координату точки числовой окружности: Р(45π/4)
Решение:
Т.к. числам t и t+2π•k (k-целое число) соответствует одна и тоже
точка числовой окружности то:
45π/4 = (10 + 5/4) • π = 10π +5π/4 = 5π/4 + 2π•5
Значит, числу 45π/4 соответствует та же точка числовой
окружности, что и числу 5π/4.
Посмотрев значение точки 5π/4 в таблице получаем:

40.

Числовая окружность
на координатной
плоскости.
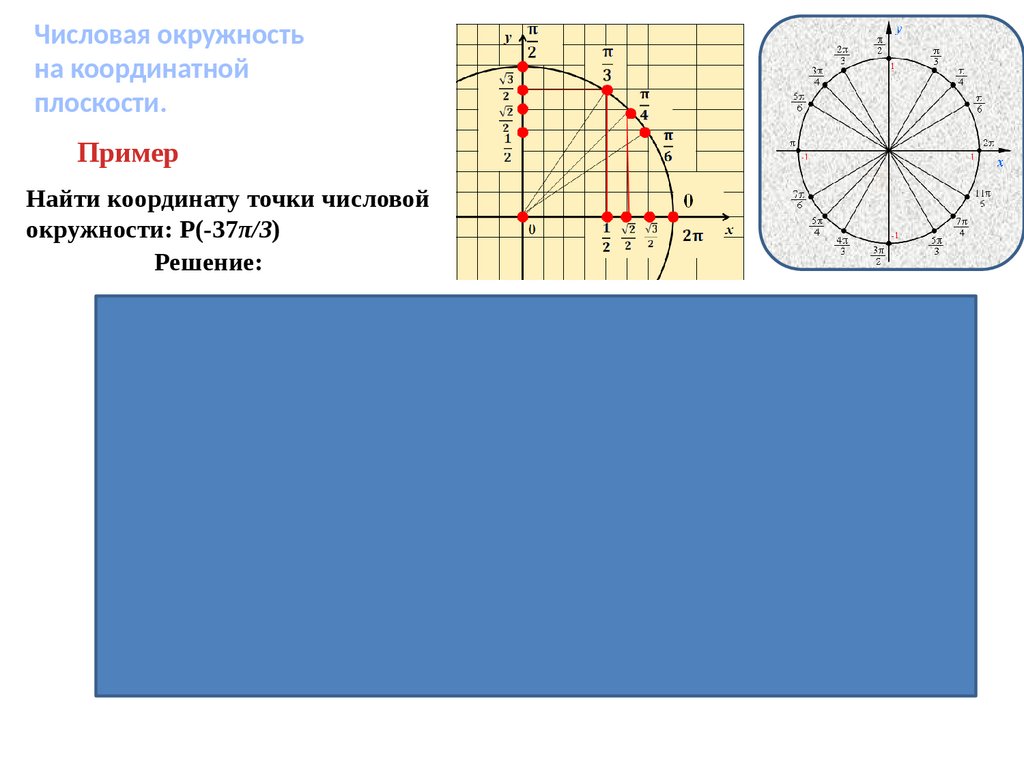
Пример
Найти координату точки числовой
окружности: Р(-37π/3)
Решение:
Т.к. числам t и t+2π•k (k-целое число) соответствует одна и тоже точка
числовой окружности то:
-37π/3 = -(12 + 1/3) • π = -12π –π/3 = -π/3 + 2π•(-6)
Значит, числу -37π/3 соответствует та же точка числовой
окружности, что и числу –π/3, а числу –π/3 соответствует та же
точка что и 5π/3. Посмотрев значение точки 5π/3 в таблице получаем:

41.

Числовая окружность
на координатной плоскости.
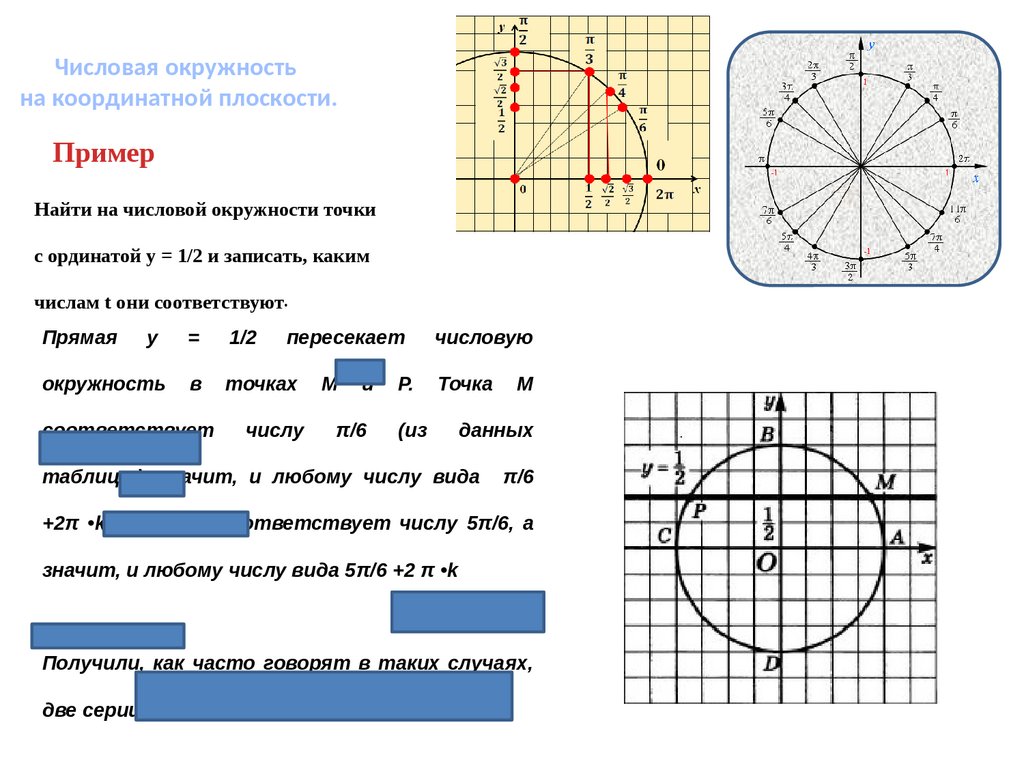
Пример
Найти на числовой окружности точки
с ординатой у = 1/2 и записать, каким
числам t они соответствуют.
Прямая
у
=
1/2
пересекает
окружность
в
точках
соответствует
числу
М
и
Р.
π/6
(из
числовую
Точка
М
данных
таблицы) значит, и любому числу вида
π/6
+2π •k . Точка Р соответствует числу 5π/6, а
значит, и любому числу вида 5π/6 +2 π •k
Получили, как часто говорят в таких случаях,
две серии значений: π/6 +2 π •k и 5π/6 +2 π •k

42.

43.

Подведение итогов урока

44.

Учитель
Домашнее задание
1) В дальнейшем для нахождения значений
синуса, косинуса, тангенса и котангенса
точек и углов необходимо выучить по
заполненным таблицам значения координат
точек, принадлежащих первой четверти т.к.
далее мы научимся выражать значения
координат всех остальных точек через
значения точек первой четверти;
2) Готовить теоретические вопросы к зачету.