Similar presentations:
Скалярний добуток векторів. Кут між векторами. 9 клас
1.
07.03.239 клас
2.
Повторимо!3.
Досі ми множили вектори на число. Виявляється, можна множити і вектор навектор. Оскільки розглядають таке множення, при якому добуток двох векторів
дорівнює числу (скаляру), то його називають скалярним добутком.
4.
5.
Кут між двома векторами – кут, що утворенийвекторами, які колінеарні даним і виходять з однієї
точки.
a
b
Кут між векторами змінюється в межах від 0о до
180о. Якщо хоча б один із векторів нульовий, то кут між
цими векторами невизначений. Кут між однаково
напрямленими векторами дорівнює 0о, а між
протилежно напрямленими – 180о.
6.
Теорема.Скалярний добуток двох векторів дорівнює добутку
їх абсолютних величин на косинус кута між ними.
7.
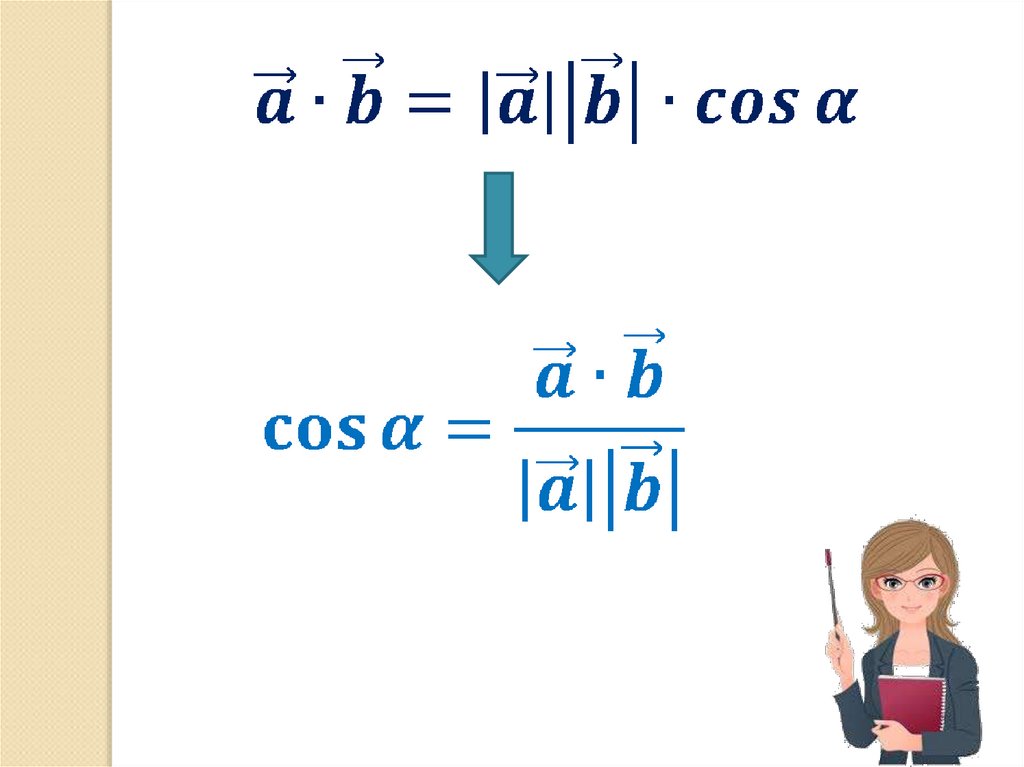
Для обчислення кута між векторамивикористовують формулу:
Наслідок.
o
Якщо a b 0 , то 0 90
о
o
Якщо a b 0 , то 90 180
o
Якщо a b 0 , то 90
і
8.
Скалярнимдобутком
двох
ненульових
векторів називають
число, що дорівнює добутку модулів
цих векторів на косинус кута між
ними.
9.
Якщо кут α – гострий, тоЯкщо кут α – тупий, то
Якщо кут α – прямий, то
10.
11.
12.
13.
14.
Приклад.Дано:
Знайти:
Розв’язання:
Відповідь:
15.
Приклад.Дано:
Знайти:
Розв’язання:
Відповідь: 5
16.
17.
Приклад.Дано:
Знайти: y
Розв’язання:
Оскільки
Відповідь: 10
18.
Приклад.Дано:
Знайти: cosα
Розв’язання:


















 mathematics
mathematics








