5.2 Definicja siły centralnej 5.3 Ruch płaski pod wpływem siły centralnej

5.4 Ruch punktu materialnego w polu sił centralnych.

1.33M

Category:

physics

Wprowadzenie do fizyki. Część piąta. Siły centralne

1. Wprowadzenie do fizyki

Mirosław Kozłowski
rok akad. 2002/2003

2. Część piąta Siły centralne

3. Siły centralne Slajd podsumowania

5.1 Historia grawitacji
5.2 Definicja siły centralnej
5.3 Ruch płaski pod wpływem siły centralnej
5.4 Ruch punktu materialnego w polu sił centralnych
5.5 Wnioski
5.6 Prawa Keplera (orbity kołowe)
5.7 Nowe układy planetarne
5.8 Zasada antropiczna
Siły centralne
3
Koniec
pokazu

4.

Linki do stron WWW
Hyper Physics
Astronomy Picture of the Day
Space Photos and Images
4

5.

http://www.planetary.org/html/society/advisors/
sagandot.html
Ziemia widziana z Voyagera 1 z odległości 6,4 bilionów
kilometrów
5

6.

http://antwrp.gsfc.nasa.gov/apod/ap980129.html
The Earth-Moon System
Credit:NEAR Spacecraft Team, JHUAPL, NASA
6

7.

Earth at Night
Credit: C. Mayhew & R. Simmon (NASA/GSFC), NOAA/NGDC, DMSP
Digital Archive
http://antwrp.gsfc.nasa.gov/apod/ap001127.html
7

8.

8
http://antwrp.gsfc.nasa.gov/apod/ap010204.html
Welcome to Planet Earth
Credit: Apollo 17 Crew, NASA

9. 5.1 Historia grawitacji

Johannes Kepler (1571-1630)
1619 - Harmonia Światów
Kwadraty okresów obiegów planet są
proporcjonalne do sześcianów promieni orbit.
2
3
T
r .
Robert Hooke (1635-1703)
Siły, dzięki którym istnieje Układ Słoneczny, a
więc siły utrzymujące planety wokół Słońca
oraz Księżyc wokół Ziemi to są te same siły,
dzięki którym jabłko spada z jabłoni.
Siły centralne
9

10.

Isaak Newton (1642-1726)
1687 - Mathematical Principles of
Natural Philosophy
1. Zasady dynamiki
d r
F ma m 2 .
dt
2
2. Grawitacja: Ruch w polu grawitacyjnym elipsa (okrąg), parabola, hiperbola.
Siły centralne
10

11.

Ruch jednostajny po okręgu:
r
2
mv
Fd
er ,
r
Fd Fd ,
2
mv
F d
.
r
Siły centralne
11

12.

Prawo Keplera (obserwacja!)
2 r
3
T
r ,
v
2
r
3
r ,
2
v
2
2
1
v ,
r
2
2
v
1
Fd
2, F
r
r
Siły centralne
12
1
.
2
r

13. 5.2 Definicja siły centralnej 5.3 Ruch płaski pod wpływem siły centralnej

5.2 Definicja siły centralnej
r
Fc F r F r r̂.
r
5.3 Ruch płaski pod wpływem siły
centralnej Fc .
a. Moment pędu
L r p.
Siły centralne
13

14.

b. Dla sił centralnych:
d Lc
0.
dt
Mamy bowiem:
dL dr d p
p r
r F.
dt dt
dt
Siły centralne
14

15.

Lc
dLc
r Fc
dt
r rˆ F r 0;
nie zmienia się w czasie.
Lc r p r mv .
Siły centralne
15

16.

Wiemy jednak, że
v rˆ r r ˆ,
r v r rˆ r r ˆ
2
r eˆ ,
L
2
Lc mr eˆL ,
2
Lc Lc m r stałe.
Siły centralne
16

17.

d Lc
2
2m r r m r 0.
dt
Dla sił centralnych:
Lc stałe mr .
2
Siły centralne
17

18. 5.4 Ruch punktu materialnego w polu sił centralnych.

F ma
2
m rˆ r r ˆ 2r r
F r rˆ.
Otrzymujemy dwa równania:
0 m 2r r ,
2
F r m r r ,
opisujące ruch punktu materialnego w polu
sił centralnych.
Siły centralne
18

19.

Równanie pierwsze
2
m r mr F r .
2
Wprowadzamy nową zmienną r=1/u i
równanie otrzymujemy w postaci:
d u
m 1 1 (*)
u
F
.
2
2
2
d
Lc u u
2
Siły centralne
19

20. 5.5 Wnioski

a. Równanie (*) jest podstawowym równaniem
ruchu opisującym ruch punktu materialnego o
masie m w polu sił centralnych F(r) F(1/u).
b. Równanie (*) jest słuszne dla dowolnej funkcji
F(r)=F(1/u).
Na przykład:
K3
K1
K2
F r ;
;
;
3
2
r
r
r
K5
K4
;
.
0.634
4.62
r
r
Siły centralne
20

21.

W zmiennej u
1
3
2
F K1u , K 2u , K 3u
u
K 4u 0.634 , K 5u 4.62 .
Makroskopowy Wszechświat można opisać
uwzględniając tylko dwa rodzaje sił:
grawitacja – prawo Newtona
elektromagnetyzm – prawo Coulomba, siła
Lorentza.
Siły centralne
21

22.

Oba rodzaje sił mają tę samą zależność od r, (u):
K
2
Fc r 2 Ku .
r
DLACZEGO?
Siły centralne
22

23.

Dla sił typu F=Ku2 otrzymujemy
równanie (*) w postaci:
2
d u
m 1
2
u
Ku
2
2
2
d
Lc u
Km
2 stała,
Lc
czyli
Siły centralne
2
d u
u W stała,
2
d
Km
W - 2 .
Lc
23
( )

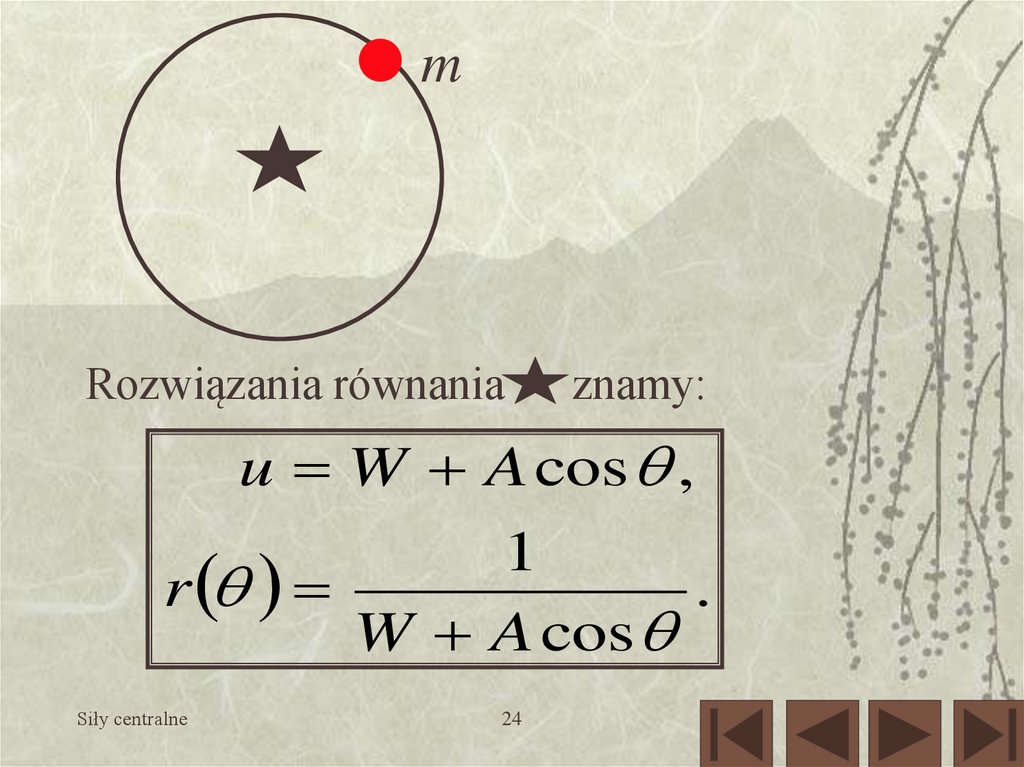
24.

m
Rozwiązania równania
znamy:
u W A cos ,
1
r
.
W A cos
Siły centralne
24

25.

W zależności od wartości stałych W
oraz A:
elipsa (okrąg),
r parabola,
hiperbola.
Siły centralne
25

26. 5.6 Prawa Keplera (orbity kołowe)

Prędkość polowa:
S r 2.
ds
Prędkość polowa ,
dt
ds
dr
2 r
2 rv,
dt
dt
ds
L
2
2 r 2 .
dt
m
ds
stałe.
dt
Siły centralne
26

27.

2 r
T
,
v
2 2
4 r
2
T
,
2
v
4 r
T
,
2
v r
2
2
2
2
2
T
4
4 r 4 am
2 3 2 4
stałe.
3
2
r
r
r
L
2
3
2
Siły centralne
27

28.

Wniosek
1. Prędkość polowa jest stała.
2. T 2/r 3 = stałe.
Siły centralne
28

29. 5.7 Nowe układy planetarne

1. Rozwiązanie równania Newtona w polu potencjału
sił centralnych V(r)
2
d u
m 1
2
u 2 2 K u ,
2
d
Lc u
K
V r
Fc 2
,
r
r
u W A cos ,
1
r
,
W A cos
Siły centralne
29
K
V r ,
r

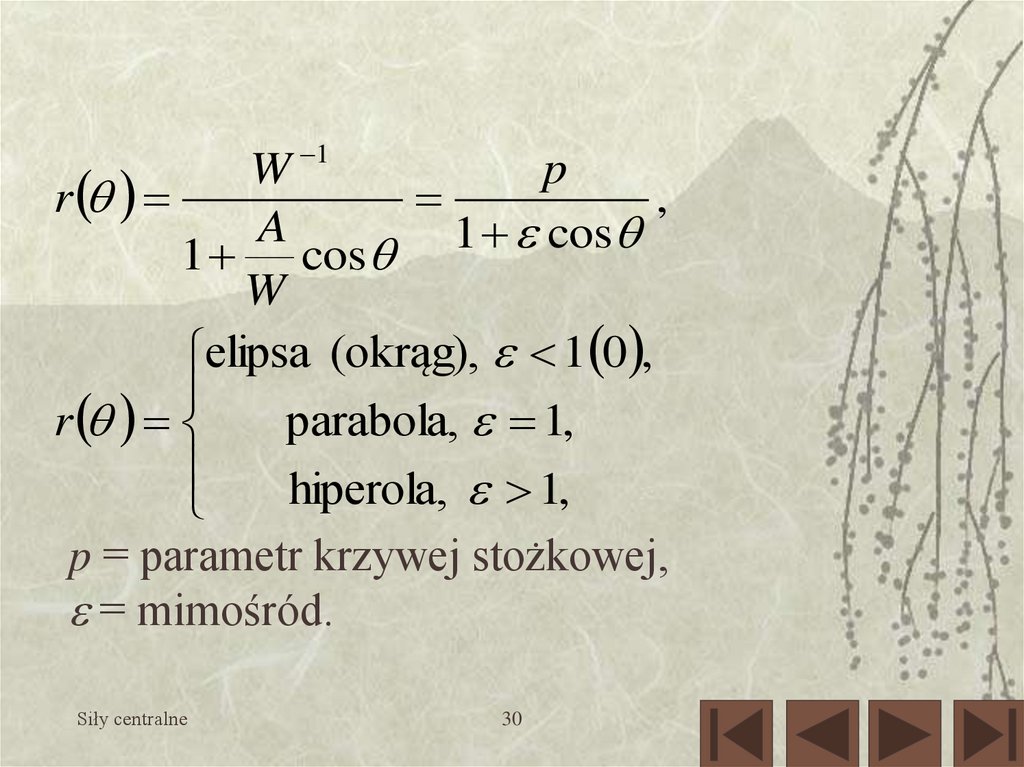
30.

1
W
p
r
,
A
1
cos
1 cos
W
elipsa (okrąg), 1 0 ,
r
parabola, 1,
hiperola, 1,
p = parametr krzywej stożkowej,
= mimośród.
Siły centralne
30

31.

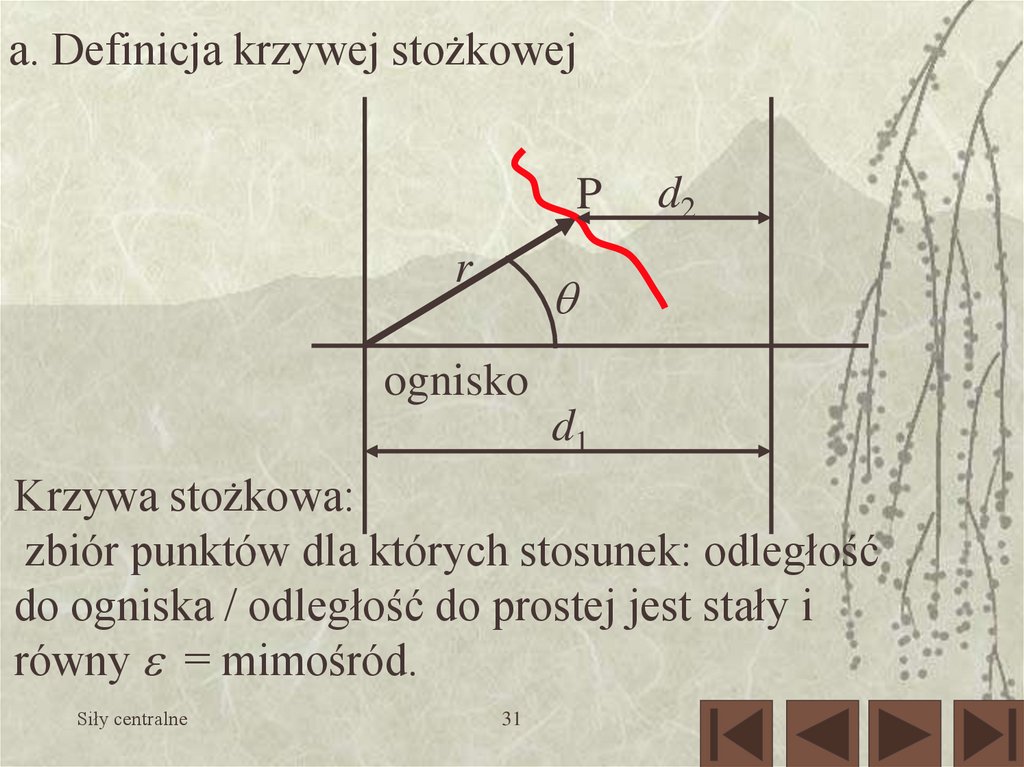
a. Definicja krzywej stożkowej
P
r
d2
ognisko
d1
Krzywa stożkowa:
zbiór punktów dla których stosunek: odległość
do ogniska / odległość do prostej jest stały i
równy = mimośród.
Siły centralne
31

32.

r
r
,
d 2 d1 r cos
d1 r cos r ,
d1
p
r
.
1 cos 1 cos
b. Prędkość radialna na krzywej stożkowej
p sin
vr r
2
1 cos
p sin
.
2
1 cos
Siły centralne
32

33.

Prawo zachowania momentu pędu
L mr θ stała B,
2
B
B 1 cos
θ
,
2
2
mr
mp
2
p sin B 1 cos B
vr
sin .
2
2
mp
mp 1 cos
2
vr stała sin .
Siły centralne
33

34.

2. Zagadnienie dwóch ciał
a. środek masy
z
z’
r1
r0
r2
'
r1
'
r2
y’
x
x’
Siły centralne
34
y

35.

a 1, 2, 3
ra ra r0 ,
va va V ,
d r0
V
.
dt
N
p ma va ma va V ma .
a 1
a
a
p p V ma .
a
Siły centralne
35

36.

Istnieje taki układ odniesienia, w którym p 0.
Układ środka masy
V
p
prędkość środka masy,
ma
a
r0
ma ra
a
m
a
Siły centralne
R,
dR
V,
dt
36

37.

R określa położenie środka masy układu
Wybieramy początek układu w R
ma ra 0,
mava 0.
a
a
Siły centralne
37

38.

b. Zagadnienie dwóch ciał.
Rozważmy dwa ciała oddziałujące na siebie za
pomocą potencjału
V r1 r2 , r r1 r2 .
Całkowita energia układu dwóch ciał:
2
2
m1r1
m2 r2
E
2
2
V r1 r2 .
Siły centralne
38
(1)

39.

Umieszczamy początek układu w środku masy
dwóch ciał. Oznacza to, że
m1r1 m2 r2 0, r r1 r2 ,
m1 r1 r2 r m1 ,
m1r1 m1r2 m1r ,
r2 m1 m2 m1r ,
r2
dr
m1
v2
u , gdzie u
.
m1 m2
dt
Siły centralne
39
m1r
,
m1 m2

40.

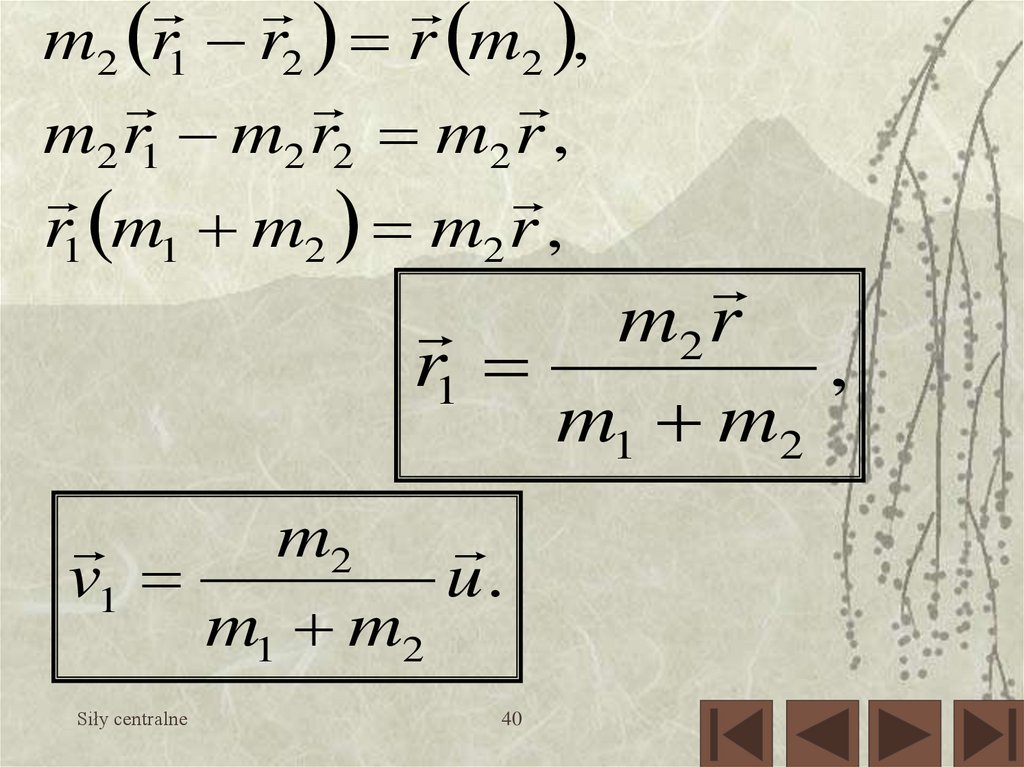
m2 r1 r2 r m2 ,
m2 r1 m2 r2 m2 r ,
r1 m1 m2 m2 r ,
m2 r
r1
,
m1 m2
v1
Siły centralne
m2
u.
m1 m2
40

41.

2
2
Stąd
m1 m2 r
m2 m1r
V r
E
2 m1 m2
2 m1 m2
2
r m1m22
m2 m12
V r
2
2
2 m1 m2
m1 m2
2
m1m2 r m2 m1
2
m m
2
2
1
m1m2
r2 V r .
2 m1 m2
2
r
(2)
E
V r . nazywamy masą zredukowaną.
2
Siły centralne
41

42.

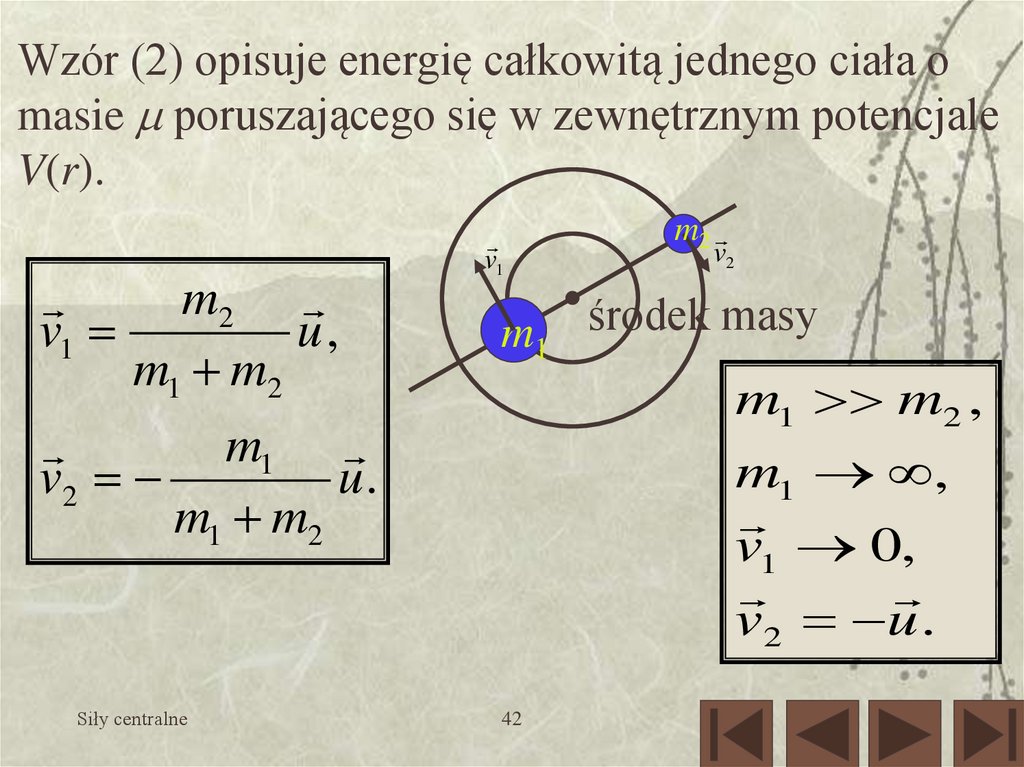
Wzór (2) opisuje energię całkowitą jednego ciała o
masie poruszającego się w zewnętrznym potencjale
V(r).
v1
m2
u,
m1 m2
v2
v1
v2
m1 środek masy
m1 m2 ,
m1
u.
m1 m2
Siły centralne
m2
m1 ,
v1 0,
v 2 u .
42

43. Nowy układ planetarny

50 lat świetlnych
~50 · 1013 km
~5 ·1014 km
1 AU 1.5 · 108 km
Obserwator na Ziemi
108 km
14
10 6.
10 km
Siły centralne
43
v
v

44. Masy Słońca i niektórych planet

Ziemia
5,97 · 1024 kg
Jowisz
1,9 · 1027 kg
Słońce
1,9 · 1030 kg
Siły centralne
44

45.

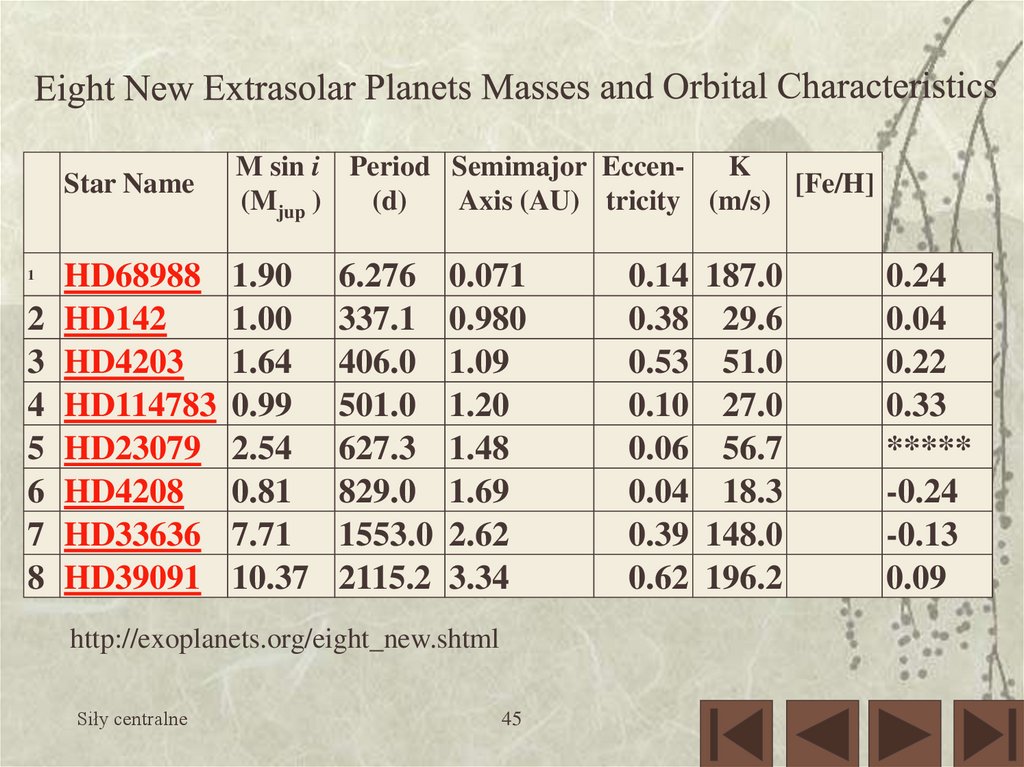
Star Name
M sin i Period Semimajor EccenK
[Fe/H]
(Mjup )
(d)
Axis (AU) tricity (m/s)
HD68988 1.90
2 HD142
1.00
3 HD4203 1.64
4 HD114783 0.99
5 HD23079 2.54
6 HD4208 0.81
7 HD33636 7.71
8 HD39091 10.37
1
6.276 0.071
337.1 0.980
406.0 1.09
501.0 1.20
627.3 1.48
829.0 1.69
1553.0 2.62
2115.2 3.34
http://exoplanets.org/eight_new.shtml
Siły centralne
45
0.14 187.0
0.38 29.6
0.53 51.0
0.10 27.0
0.06 56.7
0.04 18.3
0.39 148.0
0.62 196.2
0.24
0.04
0.22
0.33
*****
-0.24
-0.13
0.09

46.

Siły centralne
46
http://exoplanets.org/doppler.html

47.

Siły centralne
47
http://exoplanets.org/graphics/kepslaw.gif

48.

Siły centralne
48
Author: Goeff Marcy (UC Berkeley)
http://origins.stsci.edu/news/2000/01/content
/hd46375rvw.jpg
HD 46375 Radial Velocity

49.

Siły centralne
49
HD 46375 Orbit
Goeff Marcy (UC Berkeley)
http://origins.stsci.edu/news/2000/01/content/
hd46375orbitw.jpg

50.

Nowy układ planetarny
m p 2000me .
e
p
10-10m
Wprawdzie proton i elektron poruszają się wokół
wspólnego środka masy, ale praktyczne biorąc
prędkość protonu jest równa zeru. To gwarantuje
istnienie stabilnej struktury związków chemicznych.
Siły centralne
50

51. 5.8 Zasada antropiczna

Rozpatrzmy własności fizyczne innego (od naszego
Wszechświata) wszechświata, o n wymiarach
przestrzennych w którym siła grawitacji i siła
elektrostatyczna są opisywane za pomocą wzoru:*
K
F n 2 n 1 , n 2.
(1)
r
* Energia potencjalna w innym wszechświecie ma postać:
V r
K
r
2 n
Kr
,
n 2
F r
n 2 K .
V r
2 n Kr1 n
r
r n 1
We wszechświecie z n=2 nie mogą istnieć struktury biologiczne.
Siły centralne
51

52.

Równanie Newtona w innym wszechświecie:
d u
m 1 1
(2)
u 2 2 F .
2
d
L u u
Podstawiamy wzór (1) do wzoru (2) i otrzymujemy:
2
2
d u
m 1
n 1
u 2 2 n 2 Ku ,
2
d
L u
2
d u
m
n 3
u 2 n 2 Ku . ( )
2
d
L
Siły centralne
52

53.

We Wszechświecie trójwymiarowym – naszym
Wszechświecie (n = 3) równanie (2) ma
następujące rodzaje orbit:
parabola
orbity, które nie gwarantują
powstania i podtrzymania
hiperbola
życia.
elipsa – orbita stabilna, która gwarantuje
warunki do powstania i trwania życia.
Siły centralne
53

54.

W innym wszechświecie (n 3) równanie ( )
nie ma rozwiązania w postaci elipsy. Trajektorie
punktów materialnych przyciąganych przez
centrum siły (grawitacja, elektrodynamika) albo
mijają centrum i oddalają się do nieskończoności
albo spadają na centrum siły.
5
2
4
Siły centralne
54
3
1

55. Zasada antropiczna

Wszechświat musi być taki, aby dopuszczać
powstanie w nim obserwatorów.
B. Carter: Confrontation of cosmological theories with
observations, M. Longair ed. Reidel 1973.
Siły centralne
55

56. Zasada antropiczna

Jedynym prawdziwie rzeczywistym
wszechświatem jest ten, który jest
postrzegany, toteż ten rzeczywisty
wszechświat musi dostosować swoje
właściwości do warunków niezbędnych do
istnienia obserwatorów.
P.C. Davies, The anthropic principle,
Progres in Particle and Nuclear Physics, 10 (1983) 1,
Postępy Fizyki 37 (1986) 214.
Siły centralne
56

57.

57
Sir Izaak Newton zmienił obraz świata
http://antwrp.gsfc.nasa.gov/apod/ap000723.html

58.

59.

60.

Płaszczyzna ekliptyki
Płaszczyznę ekliptyki definiujemy jako płaszczyznę zawierającą orbitę Ziemi
wokół Słońca. W tej płaszczyźnie zawarte są orbity większości planet (oprócz
Neptuna). Na zdjęciu (od prawej) widzimy Księżyc oświetlony słabym
promieniowaniem Ziemi oraz planety: Saturn, Mars, Merkury.
Credit: The Clementine Project
http://antwr.gsfc.nasa.gov/apod/ap001014.html
60