Nieinercjalne układy odniesienia

1. Slajd 1

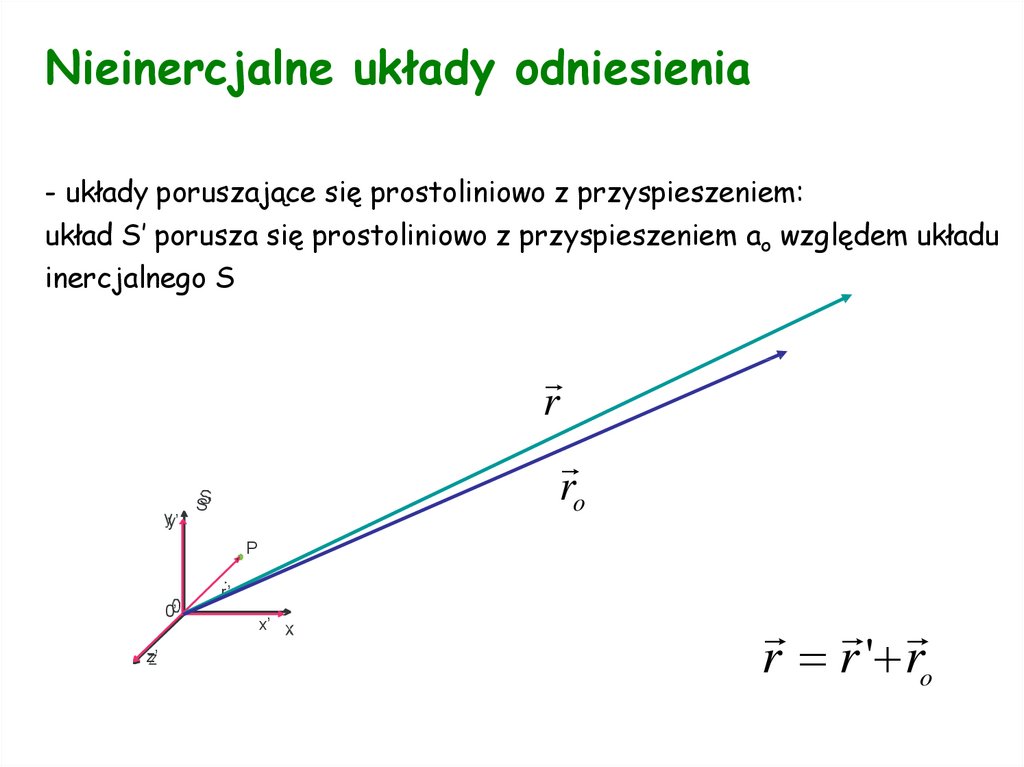
Nieinercjalne układy odniesienia
- układy poruszające się prostoliniowo z przyspieszeniem:
układ S’ porusza się prostoliniowo z przyspieszeniem ao względem układu
inercjalnego S
y’
r
ro
S’
P
r’
0’
z’
x’
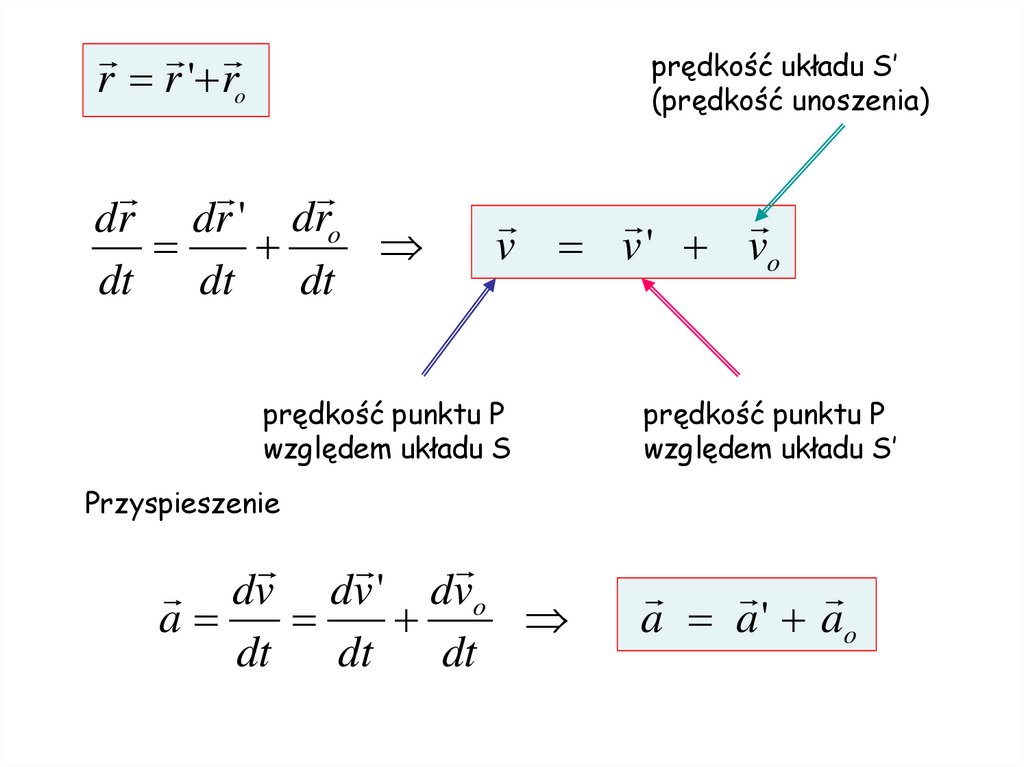
r r ' ro

2. Slajd 2

r r ' ro
prędkość układu S’
(prędkość unoszenia)
dr dr ' dro
dt dt dt
v v ' vo
prędkość punktu P
względem układu S
prędkość punktu P
względem układu S’
Przyspieszenie
dv dv ' dvo
a
dt
dt
dt
a a ' ao

3. Slajd 3

ma ma ' mao ma ' ma mao
mao Fb
siły bezwładności działające na punkt
materialny – pseudosiły, siły pozorne
Zwrot wektora sił bezwładności jest przeciwny do zwrotu wektora
przyspieszenia
ma F
siły rzeczywiście działające na punkt materialny
pochodzące od otoczenia
.
II zasada dynamiki w układzie nieinercjalnym
ma ' F Fb

4. Slajd 4

- układy obracające się:
a) siła odśrodkowa – działa na każde ciało znajdujące się w
odległości r ' od osi obrotu
2
v r
2
Fo m r ' m r ' m
r r
b) siła Coriolisa – działa na ciało poruszające się z prędkością
względem układu obracającego się
.
FC 2m v ' , FC 2m v' sin , v ' , FC , v '
v'

5. Slajd 5

Siła Coriolisa na Ziemi
FC 2m v '
aC 2 v '
ac
Gustave Gaspard de Coriolis
1792 - 1843.
v

6. Slajd 6

Czy laboratorium znajdujące się na powierzchni Ziemi jest układem
inercjalnym?
Ziemia wykonuje dwa ruchy obrotowe:
a) wokół własnej osi
przyspieszenie dośrodkowe
2
2
6
4
4
6
.
4
10
m
2
2 m
ad 1 Rz 2 Rz
3.38 10 2
2 2
T
s
24 3600 s
b) wokół Słońca
przyspieszenie dośrodkowe
ad 2 2 Rz s
4 2
4 2 1.5 1011 m
3 m
2 Rz s
5.95 10 2
2 2
T
s
365 24 3600 s
Tak, ale ze względu na niewielkie wartości przyspieszeń tę
„nieinercjalność” można pominąć w zjawiskach, które będziemy
omawiać.

7. Slajd 7

Prawo zachowania energii
• prawa zachowania są niezależne od własności toru, a często
również od własności danej siły
• prawa zachowania mają zastosowanie nawet wtedy, gdy siły są
nieznane
• prawa zachowania stanowią dogodną pomoc w rozwiązywaniu
zagadnienia ruchu cząstki.
Cząstka o masie m nie jest poddana działaniu żadnej siły. W chwili
t = 0 do cząstki przyłożono siłę
Fp
Fp const

8. Slajd 8

dv
d 2x
F p ma m m 2
dt
dt
Prędkość cząstki
v(t )
Fp
m
dt
Fp
m
t c1
Warunki początkowe
t 0, v v0 , x x0
v(t ) v0
v0 0 c1
Fp
m
t
c1 v 0
m
v t v0
t
Fp

9. Slajd 9

Z definicji
dx
v
dt
otrzymamy
Fp
Fp t 2
x(t ) v0
t dt v0t
c2
m
m 2
x0 0 c2
c2 x0
Fp t 2
x(t ) x0 v0t
m 2

10. Slajd 10

Fp t 2
Fp m 2
m
2
v(t ) v0
x(t ) x0 v0t
v0
v
(
t
)
v
0
m 2
Fp
2m Fp2
m
1
2
2
2
v(t )v0 v0 v(t ) 2v(t )v0 v0
2
Fp
m
x(t ) x0
v(t ) 2 v02
2 Fp
Fp x(t ) x0
m
m
v(t ) 2 v02
2
2

11. Slajd 11

mv 2
2
F p ( x x0 )
energia kinetyczna cząstki
praca wykonana na cząstce przez siłę
Fp
m
m 2
2
Fp x(t ) x0 v(t ) v0
2
2
praca wykonana przez przyłożoną siłę jest równa
zmianie energii kinetycznej cząstki

12. Slajd 12

Praca
– iloczyn skalarny wektorów siły i przemieszczenia
y
r1
W Fp r Fp r cos ( Fp , r )
Fp
r
Fp Fp (r ) const
r2
x
Drogę rozkładamy na N odcinków liniowych takich, że na każdym z nich
Wówczas
Fp (r ) const
N
W Fp (r1 ) r1 Fp (r2 ) r2 Fp (r3 ) r3 Fp (rN ) rN Fp (ri ) ri
równanie to jest słuszne w granicy, gdy ri 0 - toru
i 1
krzywoliniowego nie można dokładnie rozłożyć na skończoną liczbę
odcinków prostoliniowych.

13. Slajd 13

rB
i 1
rA
W lim
Fp (ri ) ri Fp (r ) dr
ri 0
Pracę definiujemy jako:
B
W A B Fp (r ) dr
A
a) Stała siła
B
W A B Fp dx Fp xB x A
F
A
Fp
W
xA
xB
x

14. Slajd 14

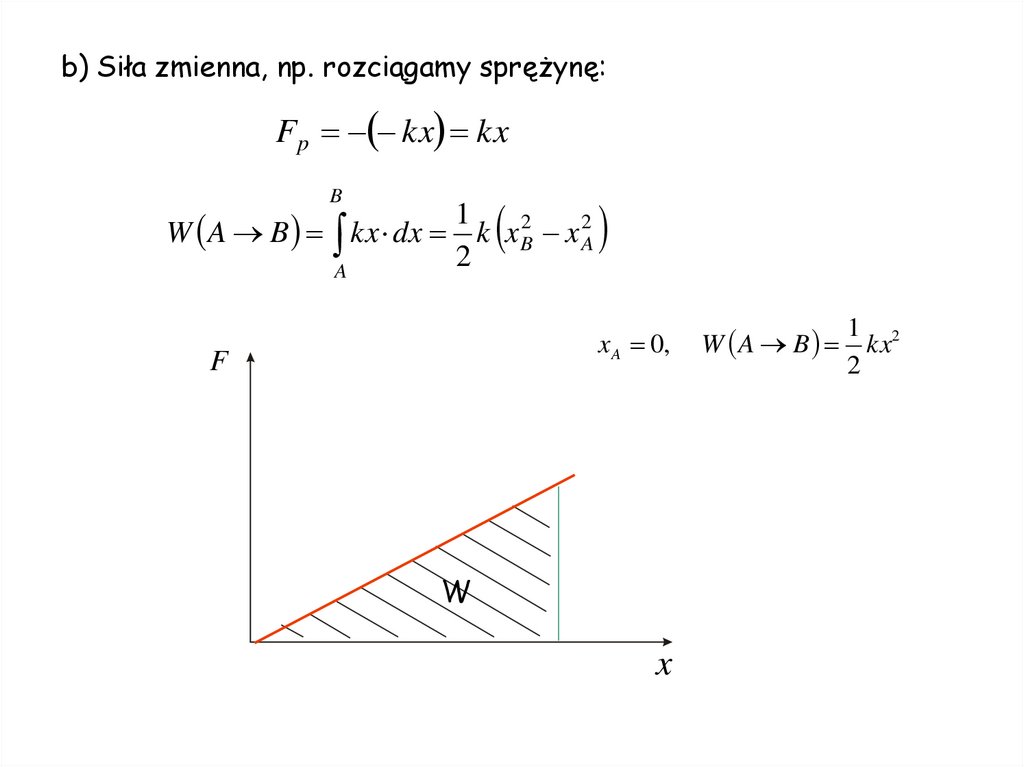
b) Siła zmienna, np. rozciągamy sprężynę:
Fp kx kx
B
1
W A B kx dx k x B2 x A2
2
A
x A 0,
F
W
x
W A B
1 2
kx
2

15. Slajd 15

Praca wykonana przez dowolną siłę
dv
Fp m
dt
?
B
B
dv
dv dr
dv
W ( A B) m dr m dt m v dt
dt
dt dt
dt
A
A
A
B
d 2 d dv dv
dv
v v v
v v
2 v
dt
dt
dt
dt
dt
B
B
m dv 2
m 2 mvB2 mvA2
W ( A B)
dt dv
2 A dt
2A
2
2
praca wykonana przez dowolną siłę = zmiana energii kinetycznej ciała

16. Slajd 16

Moc – szybkość przekazywania energii.
W
r
P
Fp
t
t
W granicy, t 0
dW
dr
P
Fp
Fp v
dt
dt
Moc chwilowa = iloczyn skalarny przyłożonej siły i prędkości chwilowej
ciała.

17. Slajd 17

Siły zachowawcze
y
mvB2 mv A2
W ( A B)
2
2
A
B
mvB2 mv A2
W ( B A)
2
2
x
mvB2 mv A2 mv A2 mvB2
0
W ( A B A)
2 2
2
2
Praca wykonana przez siłę zachowawczą po drodze zamkniętej jest
równa zeru.
Praca wykonana przez silę zachowawczą nie zależy od kształtu toru.

18. Slajd 18

Energia potencjalna
Przykładamy do ciała siłę Fp równoważącą wszystkie inne siły działające
na ciało. Wówczas Ek = const. Praca wykonana przez siłę Fp podczas
przenoszenia tego ciała z punktu A do punktu B pola zachowawczego =
zmianie energii potencjalnej ciała
E p ( B) E p ( A) W ( A B) Fp dr
B
Energia potencjalna ciała w danym punkcie pola
r
A
E p (r ) E p ( A) Fp dr
A
wyznaczona jest z dokładnością do stałej addytywnej

19. Slajd 19

Jeśli punkt A , wówczas E p ( ) 0 i energia potencjalna ciała
względem nieskończoności
r
E p (r ) Fp dr
F
Jeśli siłę przyłożoną zastąpimy siłą
rzeczywiście działającą na ciało
Fp F to energia potencjalna ciała w danym punkcie pola
E p (r ) E p ( A) F dr
r
A
lub względem punktu położonego w nieskończoności
r
E p (r ) F dr

20. Slajd 20

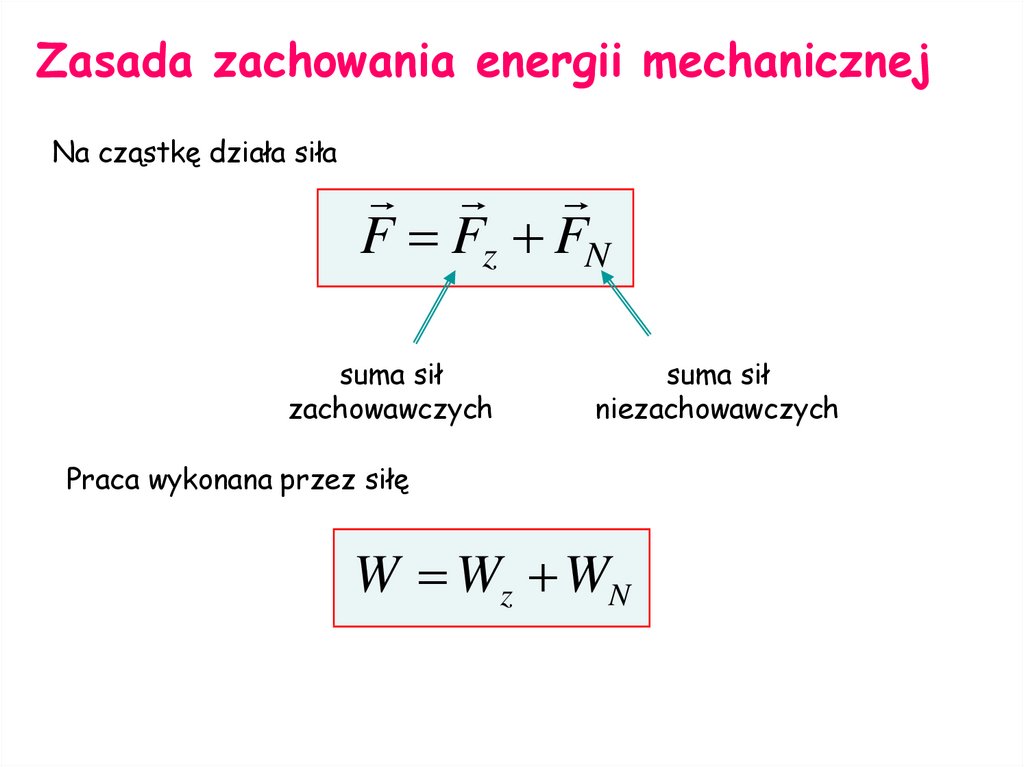
Zasada zachowania energii mechanicznej
Na cząstkę działa siła
F Fz FN
suma sił
zachowawczych
suma sił
niezachowawczych
Praca wykonana przez siłę
W Wz WN

21. Slajd 21

Praca wykonana przez dowolne siły podczas przenoszenia ciała z
punktu A do B = zmianie energii kinetycznej ciała
W W ( A B) EkB EkA
Praca wykonana przez siły zachowawcze = zmianie energii
potencjalnej ciała
Wz W ( A B) E pB E pA
EkB EkA E pB E pA WN

22. Slajd 22

EkB E pB EkA E pA WN
energia całkowita
w punkcie B pola
energia całkowita
w punkcie A pola
E EcB EcA WN
E 0
E const
WN 0
FN 0
Zmiana całkowitej energii mechanicznej układu równa
jest pracy sił niezachowawczych.
Jeśli na ciało (układ ciał) działają tylko siły
zachowawcze wówczas energia mechaniczna jest stała.

23. Slajd 23

Prawa zachowania w nieinercjalnych układach
odniesienia
EcB EcA WN WB
Odśrodkowa siła bezwładności
2
FB m R
a praca przez nią wykonana
B
2
WB FB dr m Rdr
B
A
przy czym
A
Rdr Rdr cos ( Rdr ) RdR
zmiana promienia

24. Slajd 24

2 RB
RB
2
2 R
WB m R dR m
2
RA
RA
2
2
R
R
m 2 B m 2 A
2
2
Praca wykonana przez siłę bezwładności nie zależy od drogi łączącej
punkty A i B – jest więc siłą zachowawczą. Zmiana energii
potencjalnej
E pB E pA WB
2
2
R
R
2
2
A
E pB E pA m
m B
2
2
Energia potencjalna w dowolnym punkcie:
E pB
2
2
2
R
R
R
E pA m 2 A m 2 B m 2 B const
2
2
2
const

25. Slajd 25

Związek siły z energią potencjalną
Przypadek jednowymiarowy – F = F(x)
x
E p ( x) Fx dx
dE p ( x) Fx dx
Fx
dE p
dx
Przypadek trójwymiarowy – F = F(x,y,z)
Fx
E p
x
, Fy
E p
y
, Fz
E p
z
E p E p E p
F i
j
k
i
j k E p gradE p
x
y
z
y
z
x
operator gradientu

26. Slajd 26

Operator gradientu
Każdemu punktowi o współrzędnych (x, y, z) przypisana jest wielkość
skalarna = (x, y, z), to dane pole jest polem skalarnym
grad i
j
k
x
y
z
przy przemieszczeniu o odcinek
dr i dx j dy k dz
następuje przyrost funkcji o wartość
d grad dr
dx
dy
dz
x
y
z

27. Slajd 27

wektor
E p ( x, y, z ) E p ( x, y, z ) E p ( x, y, z )
F i
j
k
x
y
z
i
j
k E p ( x, y, z ) grad E p ( x, y, z )
y
z
x
grad
skalar
wektor
wektor · skalar = wektor
wektor · wektor = skalar
wektor x wektor = wektor
a
a
a
gradient
diwergencj a
rotacja