Введение. Метод проекций как основа построения чертежа. Точка в ортогональной системе координат. Лекция 1

1.

Лекция 1.Введение. Метод
проекций как основа
построения чертежа. Точка в
ортогональной системе
координат.
Инженерная и компьютерная графика Б1.В.07
09.03.01. Информатика и вычислительная техника
Доцент Ткачук Евгений Остапович
2019/2020

2.

Структура учебной дисциплины, модульнорейтинговая система оценки
• Модуль 1 (50 баллов).
• Модуль содержит 6 лекционных занятий, 1 практическое
занятие, 2 лабораторных занятия, 1 домашнее задание. Знание
лекционного материала оценивается по результатам тестового
контроля, максимальное количество баллов за тестовый
контроль составляет 10. За выполненное и защищенное
практическое занятие - максимум 10 баллов. За выполненное и
защищенное лабораторное занятие - максимум 10 баллов. За
выполненное и защищённое домашнее задание - максимум 10
баллов. Общее максимальное количество баллов за модуль 1
составляет 50

3.

• Модуль 2 (50 баллов).
• Модуль содержит 2 лекционных занятий, 1 практическое занятие, 4
лабораторных занятия, 2 домашних задания. Знание лекционного
материала оценивается по результатам тестового контроля,
максимальное количество баллов за тестовый контроль составляет
10. За выполненное и защищённое практическое занятие - максимум 5
баллов. За выполненное и защищённое лабораторное занятие максимум 5 баллов. За выполненное и защищённое домашнее задание
№2 - максимум 7 баллов, домашнее задание №3 – 8 баллов. Общее
максимальное количество баллов за модуль 2 составляет 50.

4.

Распределение баллов по блокам модулей
дисциплины «Инженерная и компьютерная
графика»
Модуль
Модуль 1
50
10
Практический блок
(Распределение
баллов по
занятиям)
40=10+10+10+10
Модуль 2
50
10
40=5+5+5+5+5+7+8
Зачет
Всего баллов Теоретический
(Максимальн блок
ое значение) (тестирование)
100
Для получения зачета студенту достаточно набрать 41 и более
баллов.

5.

Рекомендуемая литература
• Большаков В.П., Тозик В.Т., Чагина А.В. Инженерная
и компьютерная графика Спб. «БХВ-Петербург». 2013.
• Основы начертательной геометрии. Краткий курс и
сборник задач.: Учебное пособие/Буланже Г. В.,
Гущин И. А., Гончарова В. А. http://znanium.com/catalog.php?bookinfo=479429
• Начертательная геометрия: Учебник / С.А. Фролов.
http://znanium.com/catalog.php?bookinfo=489831
• Забелин А.В. ОСНОВЫ НАЧЕРТАТЕЛЬНОЙ ГЕОМЕТРИИ.
Под редакцией зав. кафедрой «Инженерная графика»
ТГТУ д.т.н., профессора В.И.Горячева. 2006 год.
http://window.edu.ru/resource/651/58651/files/tstu-tver53.pdf

6.

Структура курса
• Учебный курс «Инженерная и компьютерная графика» условно
можно разбить на три раздела:
• элементы начертательной геометрии;
• элементы черчения и конструирования;
• элементы компьютерной графики.

7.

Предмет начертательной геометрии
• Начертательная геометрия изучает методы изображения
пространственных геометрических фигур на плоскости, а также
сами эти фигуры по их изображениям.
• Среди других ветвей геометрии, начертательную геометрию
выделяет то, что для решения общегеометрических задач она
использует графический способ.

8.

Хронология развития начертательной геометрии
• Альберти Леон Баттиста (1404-1472) – итальянский философ и
архитектор, сформулировал основы теоретической перспективы.
• Леонардо да Винчи (1452-1519) – итальянский художник и ученый,
дополнил линейную перспективу учением « об уменьшении цветов и
отчетливости очертаний», что позволило ему получать удивительно
рельефные реалистичные изображения.
• Альбрехт Дюрер (1471-1528) – немецкий математик, художники гравер,
высказывал идеи об ортогональном проецировании пространственных
фигур на плоскость, разработал метод ортогонального изображения
конических сечений и способ построения перспективы по двум
ортогональным проекциям предмета.
• Гаспар Монж (1746-1818) – французский геометр и инженер, обобщил
все научные труды предшественников, всю теорию о методах
изображения пространственных фигур и создал единую науку об
ортогональном проецировании – начертательную геометрию. В
своем труде «Начертательная геометрия», изданном в 1798году, он
определил ее как «искусство представлять на листе бумаги,
имеющем только два измерения, предметы, имеющие три размера,
которые подчинены точному определению».

9.

Виды, способы проецирования.
Начертательная геометрия является одним из
разделов геометрии, в котором пространственные
фигуры (оригиналы), представляющие собой
совокупность геометрических элементов, изучаются
по их изображениям на плоскости (или какой-либо
другой поверхности).
• К геометрическим элементам относятся:
• точка — бесконечно малая величина, не имеющая
размера;
• линия — состоящая из последовательности
бесчисленного множества точек;
• поверхность — состоящая из совокупности
множества точек и не имеющая толщины.

10.

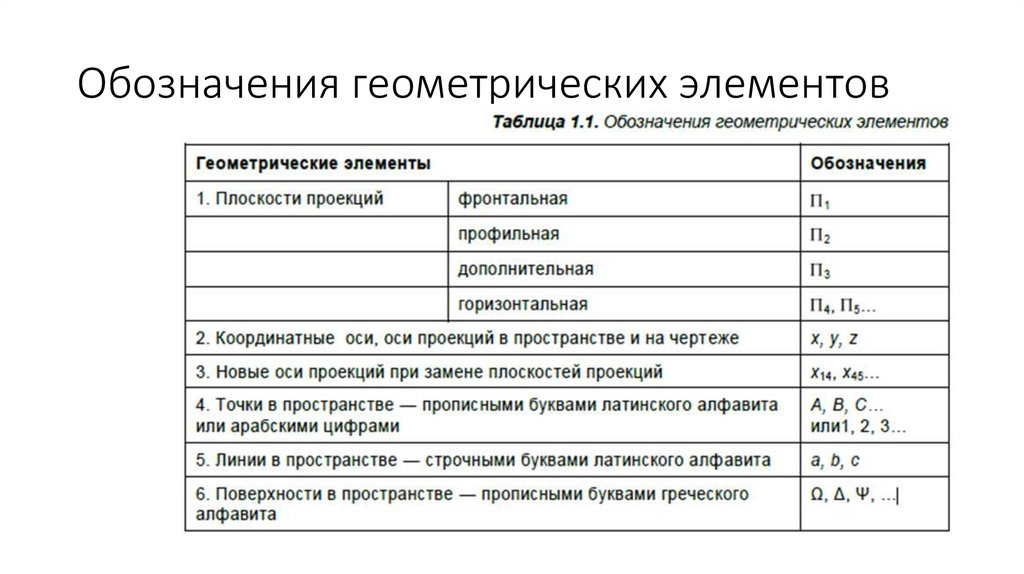
Обозначения геометрических элементов

11.

Обозначения геометрических элементов
(продолжение)

12.

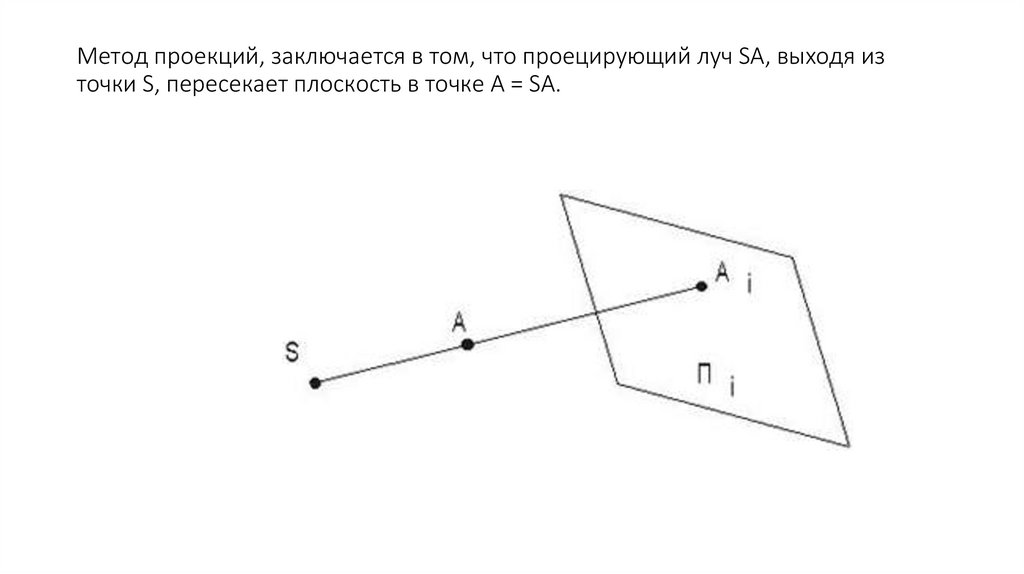
Метод проекций, заключается в том, что проецирующий луч SA, выходя из
точки S, пересекает плоскость в точке А = SA.

13.

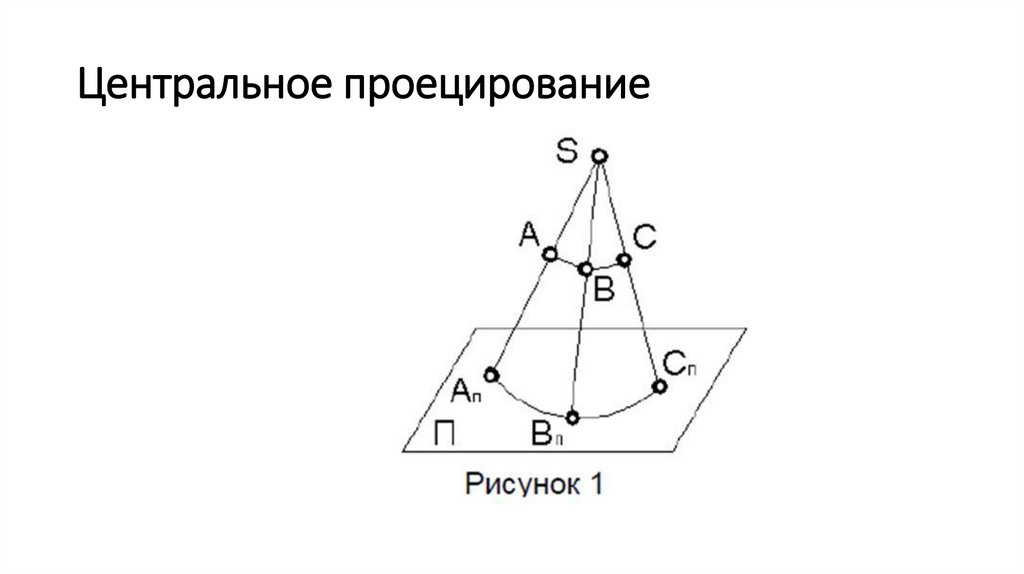
Центральное проецирование

14.

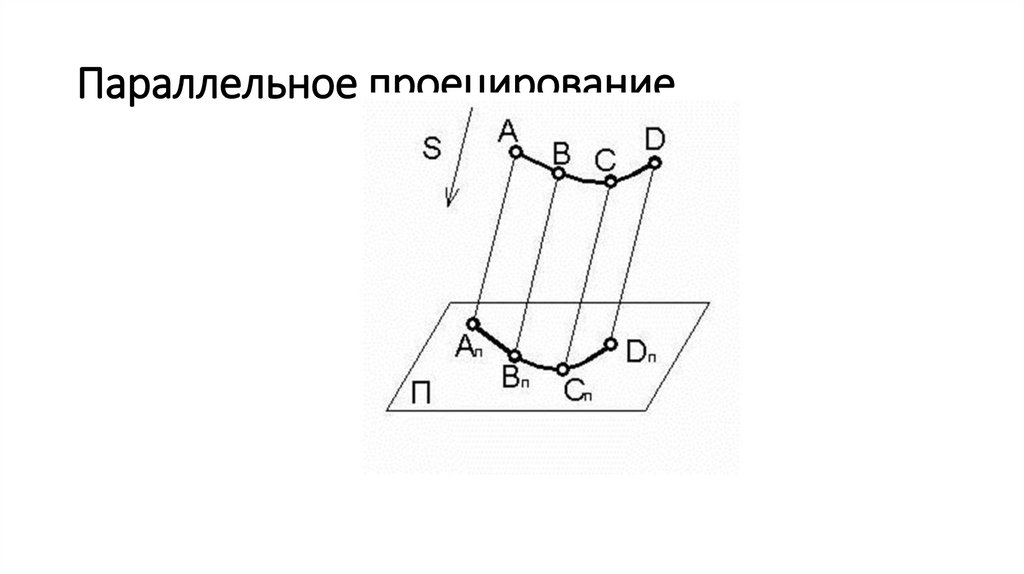
Параллельное проецирование

15.

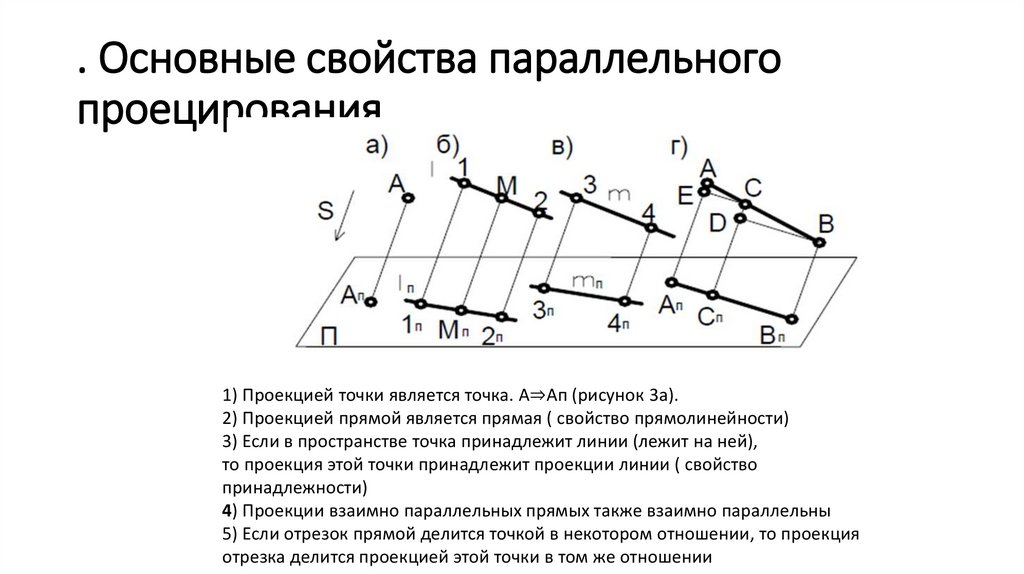
. Основные свойства параллельного
проецирования
1) Проекцией точки является точка. А⇒Ап (рисунок 3а).
2) Проекцией прямой является прямая ( свойство прямолинейности)
3) Если в пространстве точка принадлежит линии (лежит на ней),
то проекция этой точки принадлежит проекции линии ( свойство
принадлежности)
4) Проекции взаимно параллельных прямых также взаимно параллельны
5) Если отрезок прямой делится точкой в некотором отношении, то проекция
отрезка делится проекцией этой точки в том же отношении

16.

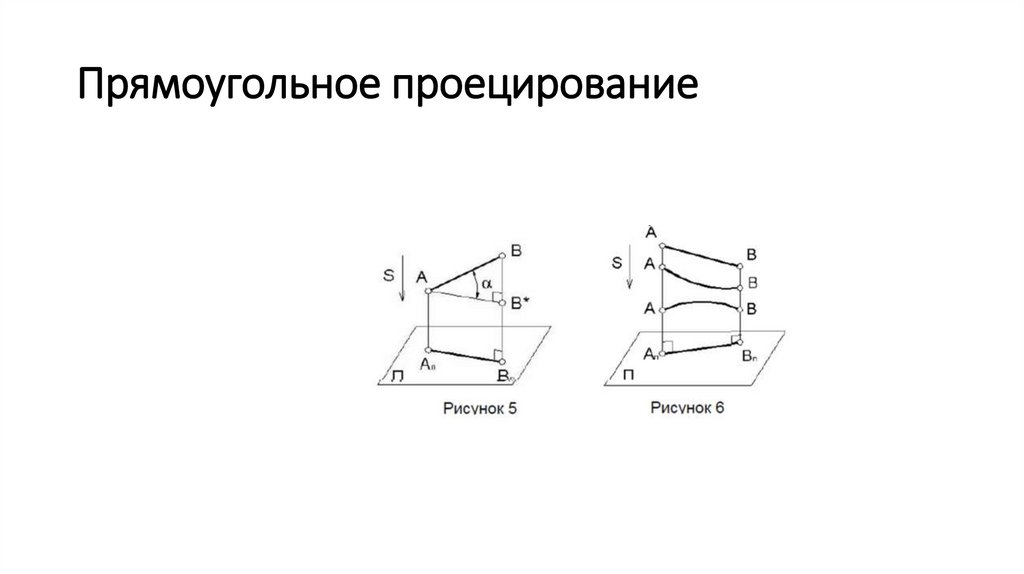
Прямоугольное проецирование

17.

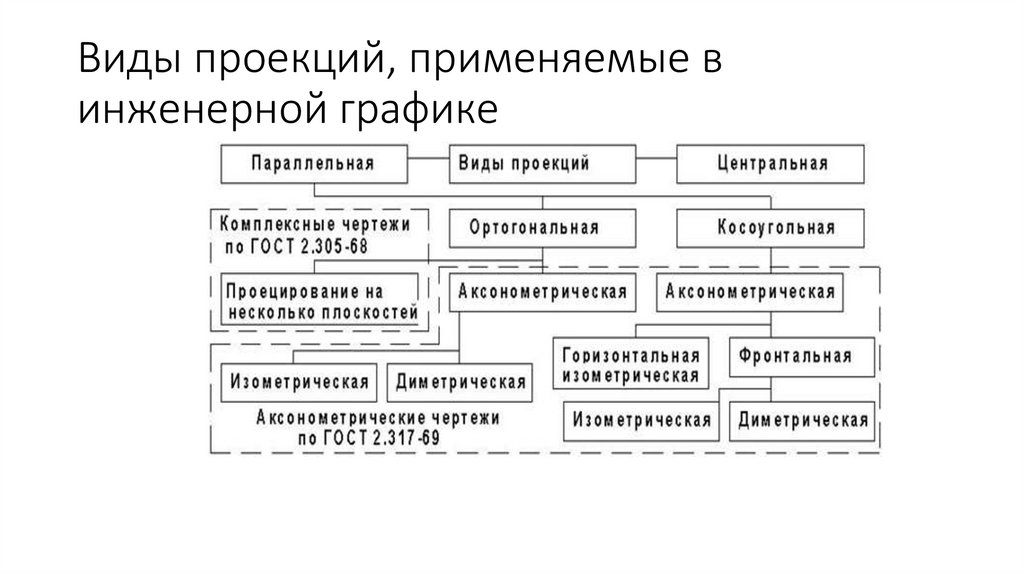
Виды проекций, применяемые в
инженерной графике

18.

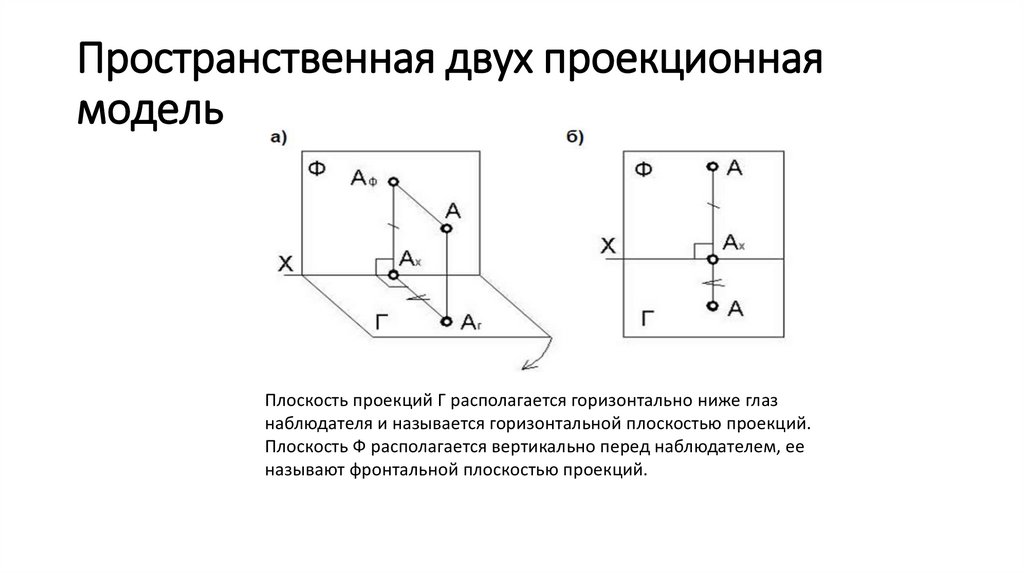
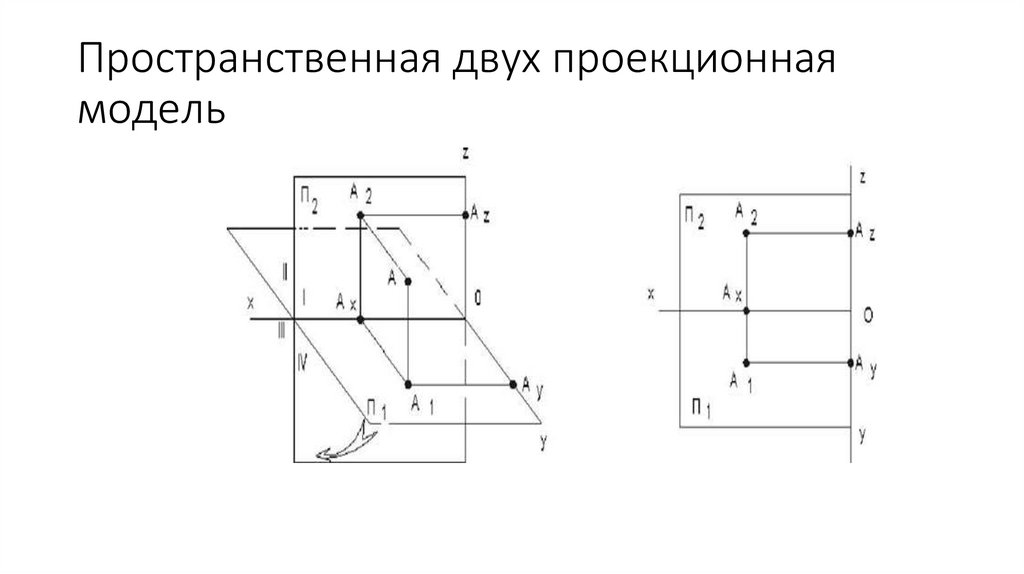
Пространственная двух проекционная
модель
Плоскость проекций Г располагается горизонтально ниже глаз
наблюдателя и называется горизонтальной плоскостью проекций.
Плоскость Ф располагается вертикально перед наблюдателем, ее
называют фронтальной плоскостью проекций.

19.

Пространственная двух проекционная
модель

20.

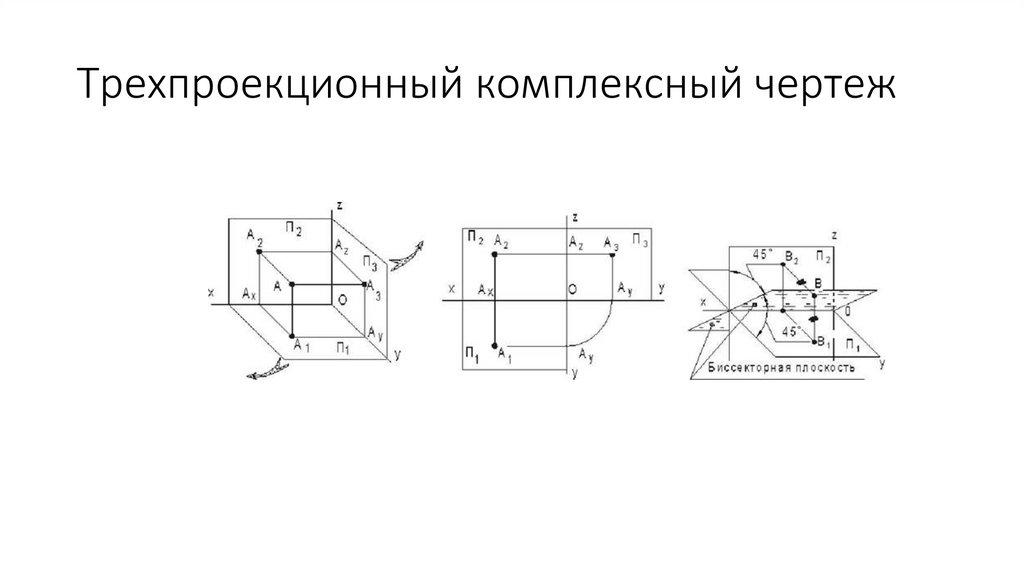
Трехпроекционный комплексный чертеж

21.

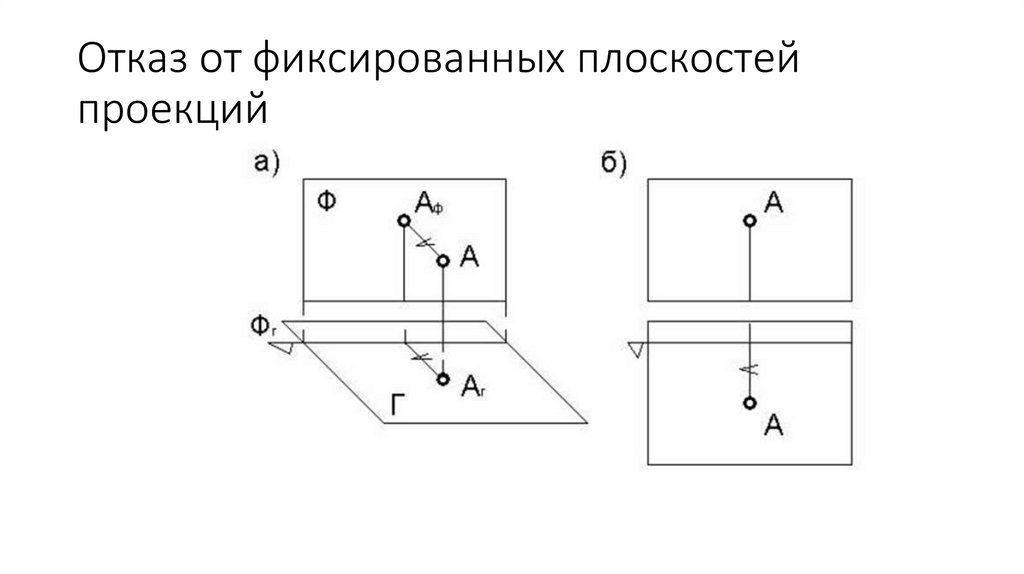
Отказ от фиксированных плоскостей
проекций

22.

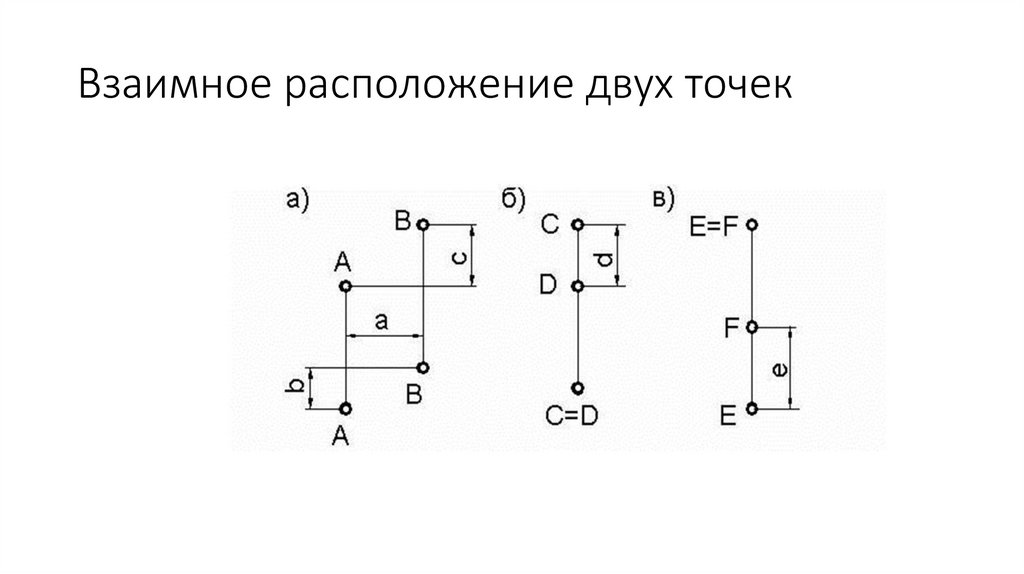
ОСНОВНЫЕ ПОЗИЦИОННЫЕ ЗАДАЧИ
• Позиционными называют задачи, в которых
определяется взаимное расположение различных
геометрических фигур.
• К таким задачам относятся задачи на
взаимопринадлежность (построение точки на линии или
поверхности,
• проведение линии на поверхности или поверхности
через заданные линии и другие)
• на пересечение (пересечение линии с плоскостью и
поверхностью, пересечение плоскости с плоскостью и
поверхностью, пересечение поверхностей).
• Различают « прямые» и « обратные» позиционные
задачи. В прямых задачах необходимо построить
чертежи оригиналов, расположенных определенным
образом относительно друг друга.
• В обратных позиционных задачах по имеющемуся
чертежу определяется взаимное расположение точек,
прямых и плоскостей относительно друг друга

23.

Взаимное расположение двух точек