Similar presentations:
Метод проекций. Проекции точки
1.
Инженерная графика1 семестр
для студентов гр. ИУ 8
Семинар 2
Метод проекций
Проекции точки
Подготовили:
доценты кафедры РК-1 Сенченкова Л.С., Палий Н.В.
2.
ВведениеПредметы (пространственные формы) в евклидовом пространстве
имеют три измерения. Изображения на плоскости – двухмерные. На плоскости
могут быть изображены только линии.
Пространственные формы ограничены поверхностями.
Поверхность – результат перемещения линии в пространстве (линия –
образующая поверхности). Перемещение линии также может быть задано с
помощью линий (линия – направляющая поверхности).
Линия – результат перемещения в пространстве точки или результат
пересечения поверхностей. Линия – однопараметрическое множество точек.
Точка – элементарный геометрический объект. Точка – результат
пересечения двух линий. Точка – элемент множества (пространства).
Т. о., любая поверхность может быть представлена как некоторое
упорядоченное, двухпараметрическое множество точек.
Пространство представляет собой множество точек.
3.
1. Метод проекцийВ основе правил построения изображений,
рассматриваемых в начертательной геометрии и
применяемых в инженерной практике, лежит метод
проекций. Так как пространственные формы
рассматриваются как множество принадлежащих
им точек, то все правила будем рассматривать на
примере построения проекций точки.
4.
Принятые обозначенияВ пространстве
На плоскости
точки
A, B, C…
A′; B′; C′; A′′; B′′; C′′…
линии
a , b , c , l…
a′; b′; … a′′; b′′…
поверхности
α, β, γ…
α′; β′; γ′…
5.
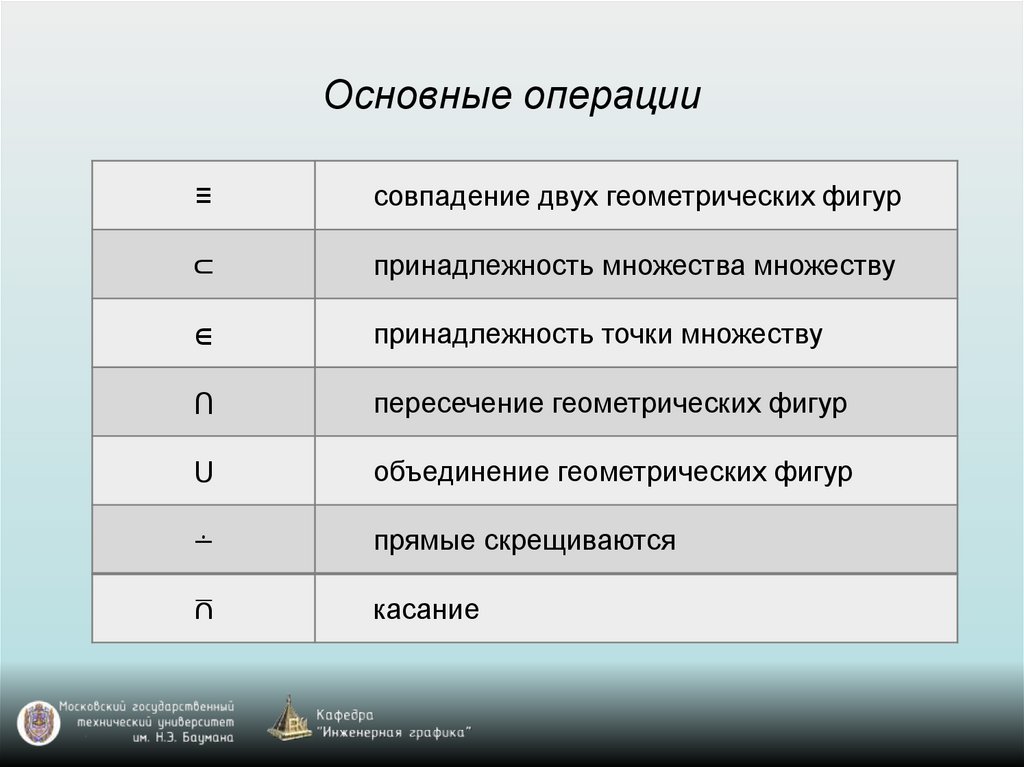
Основные операции≡
совпадение двух геометрических фигур
⊂
принадлежность множества множеству
∊
принадлежность точки множеству
⋂
пересечение геометрических фигур
⋃
объединение геометрических фигур
∸
прямые скрещиваются
⩃
касание
6.
Условия получения изображений1) Каждому предмету должно соответствовать
только ему присущее изображение на плоскости.
2) Каждому изображению должен соответствовать
только один предмет пространства с заданными
геометрическими характеристиками (форма,
размер, положение в пространстве).
7.
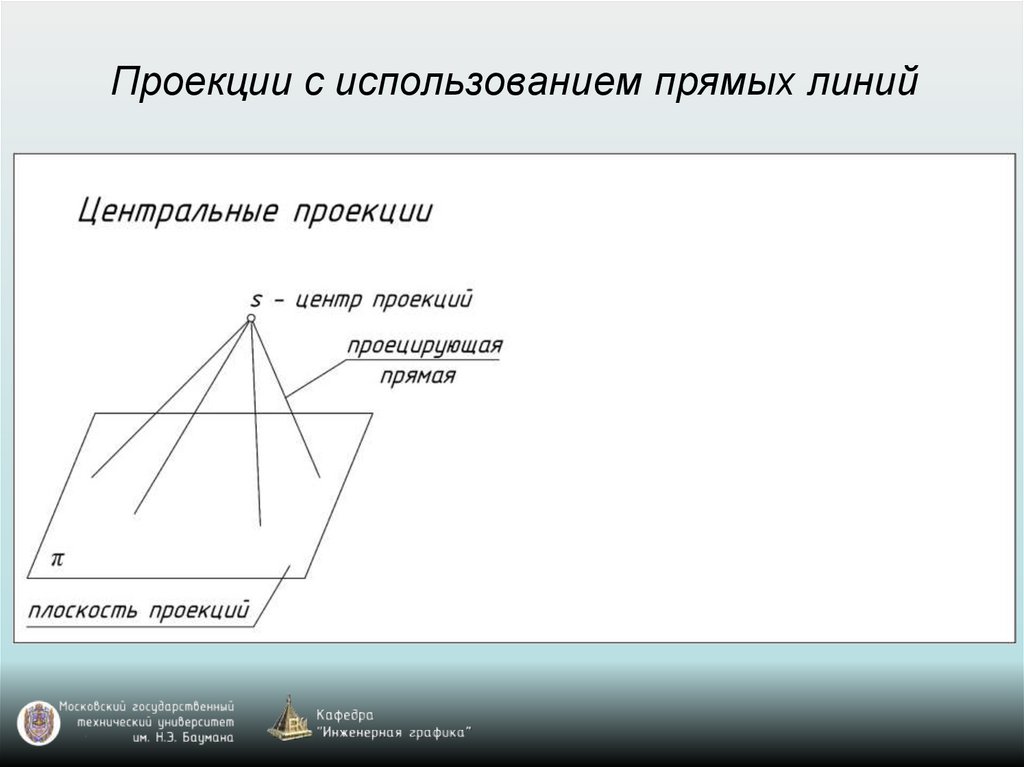
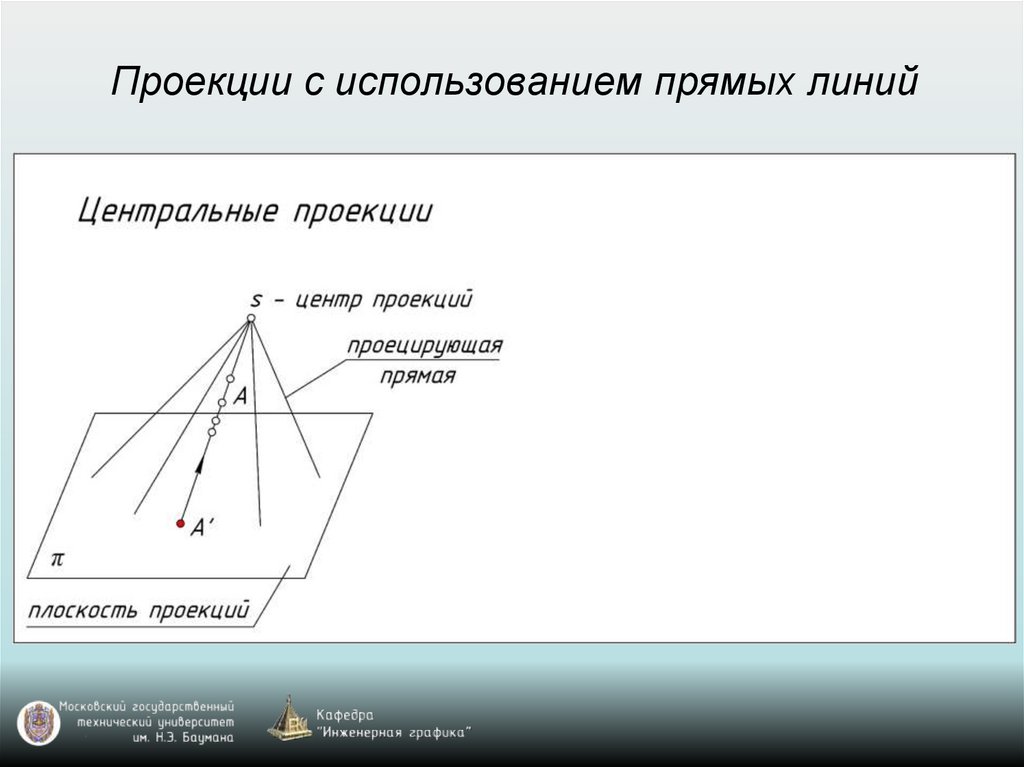
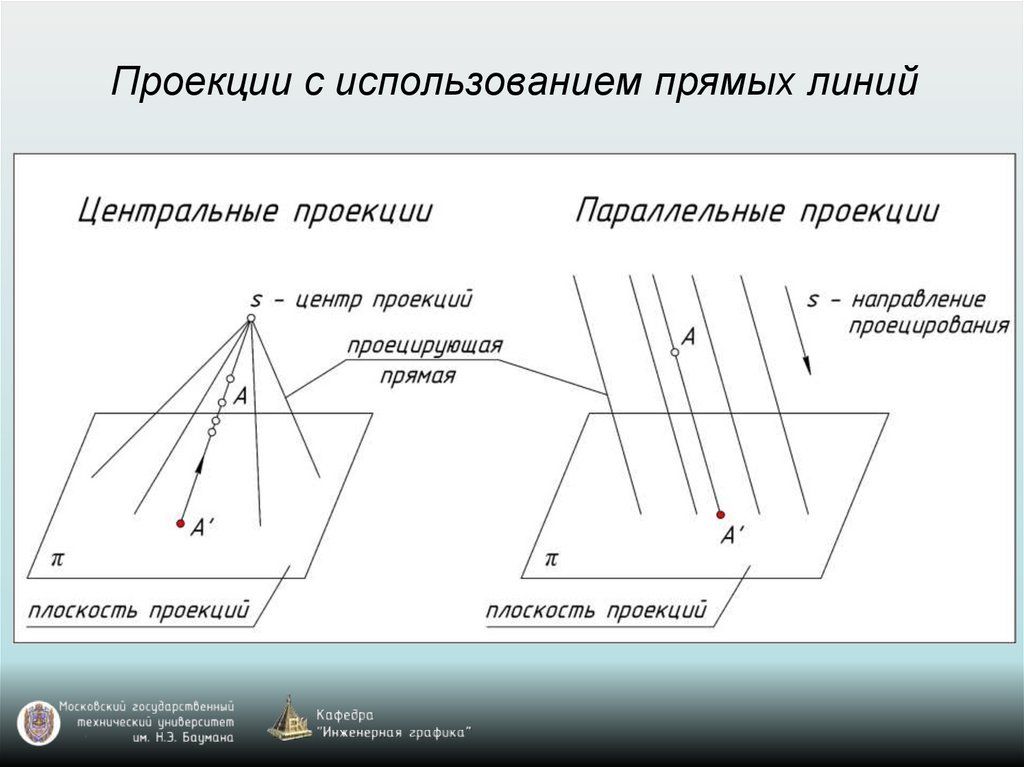
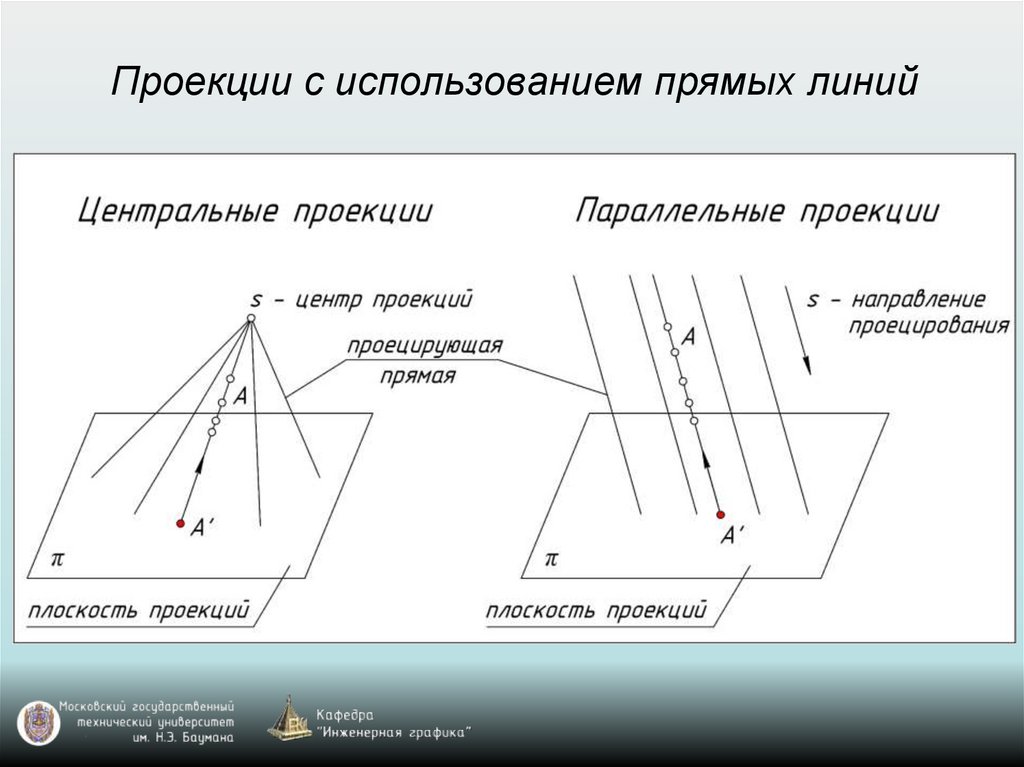
Проекции с использованием прямых линий8.
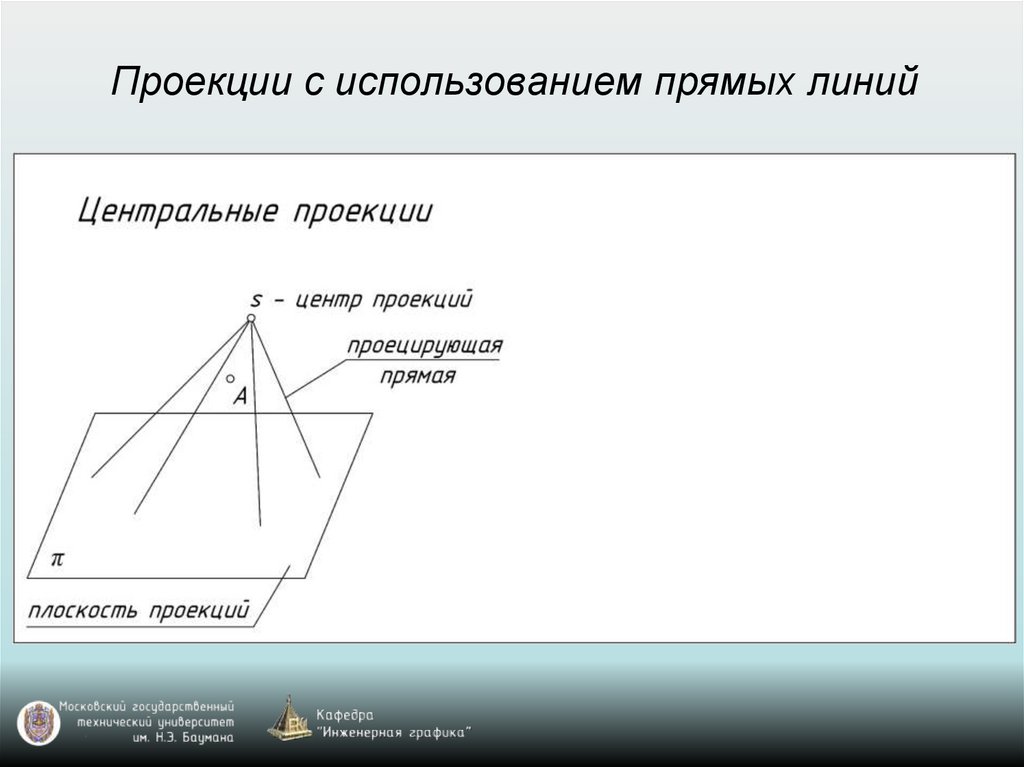
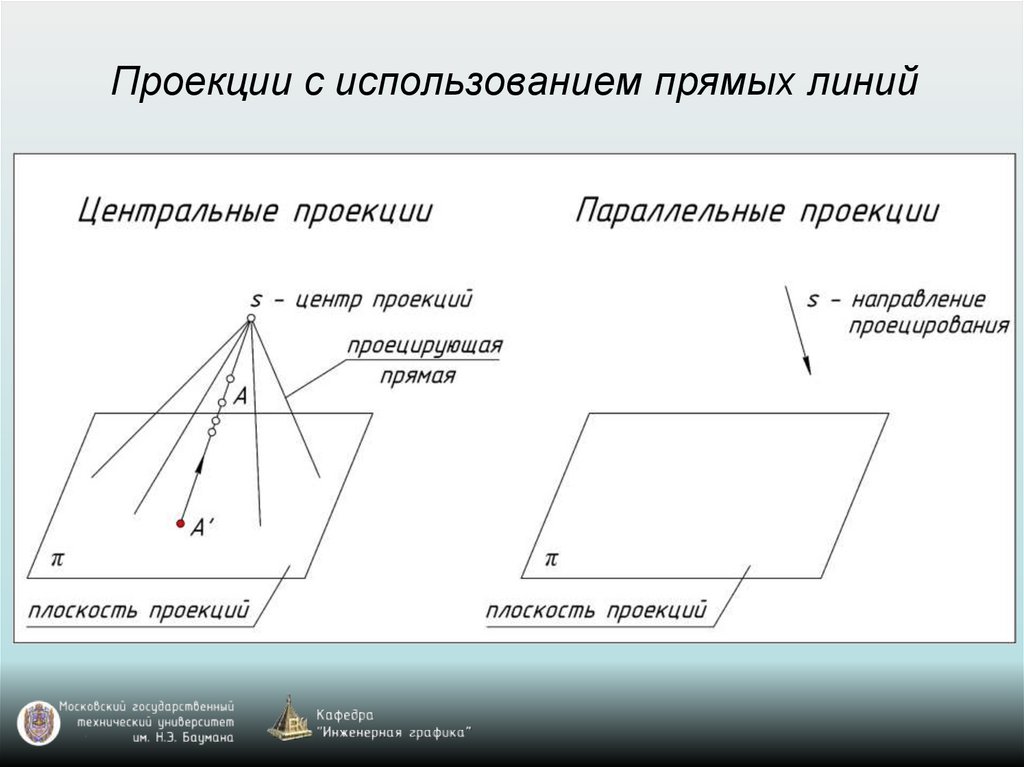
Проекции с использованием прямых линий9.
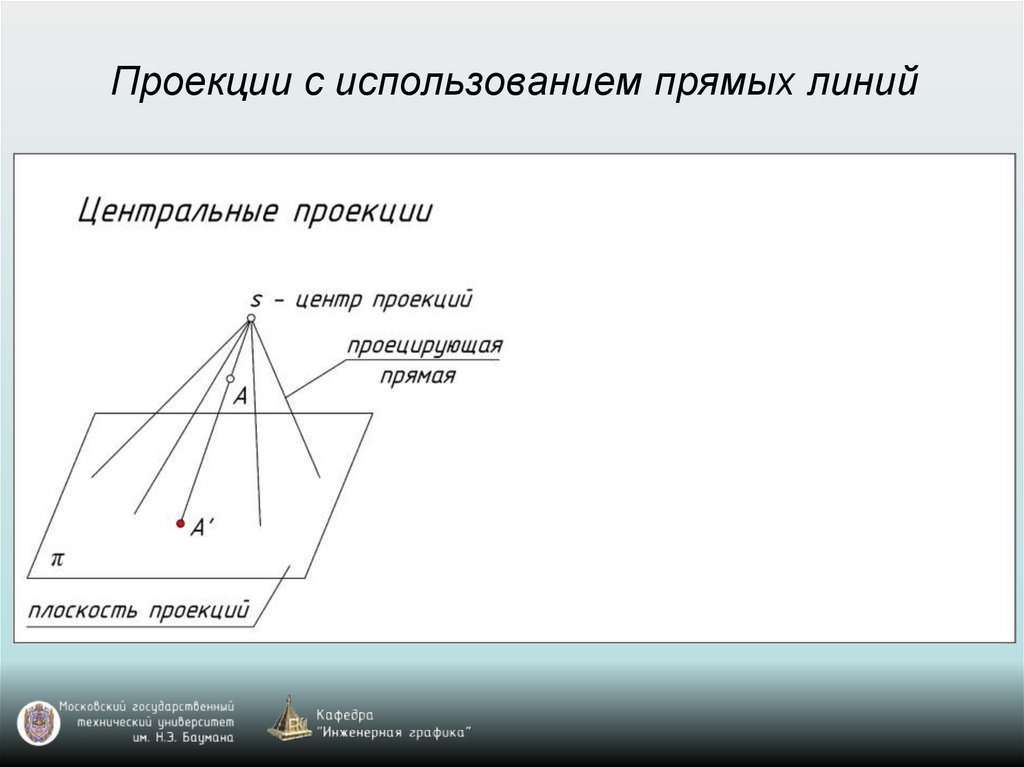
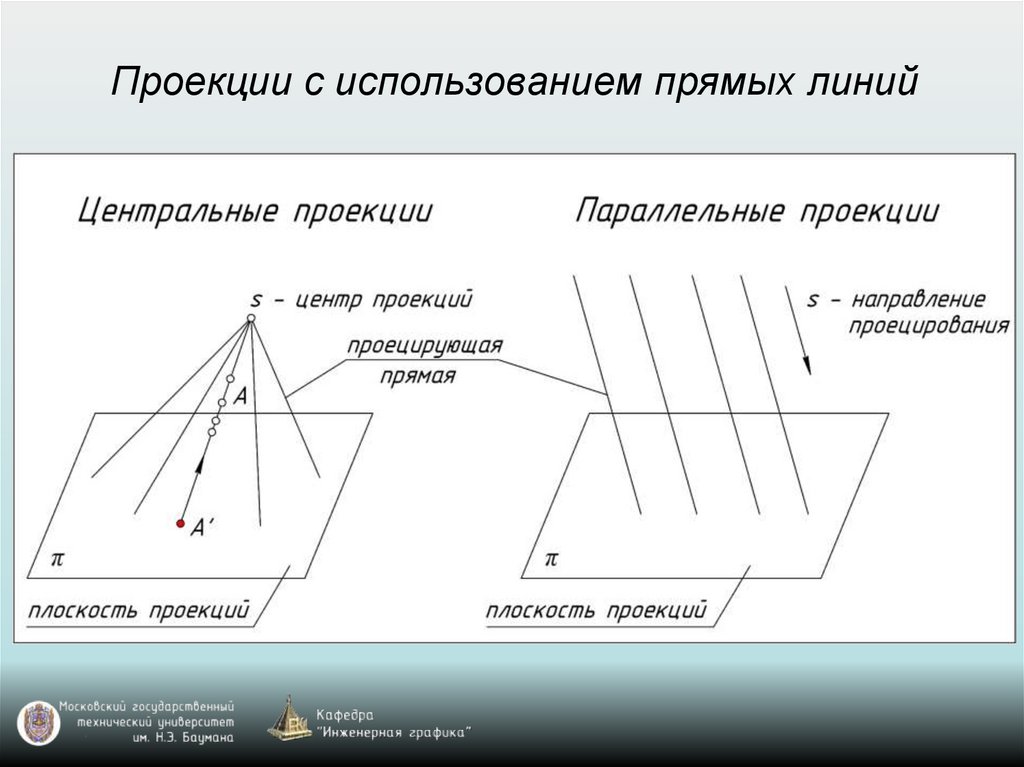
Проекции с использованием прямых линий10.
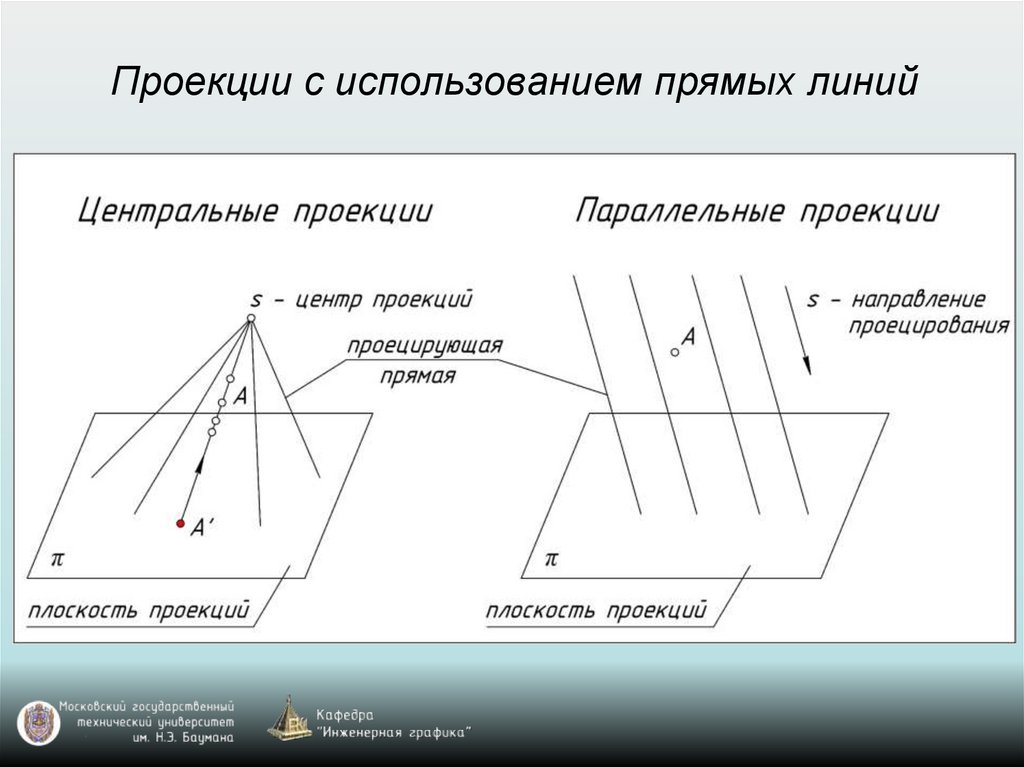
Проекции с использованием прямых линий11.
Проекции с использованием прямых линий12.
Проекции с использованием прямых линий13.
Проекции с использованием прямых линий14.
Проекции с использованием прямых линий15.
Проекции с использованием прямых линий16.
Проекции с использованием прямых линий17.
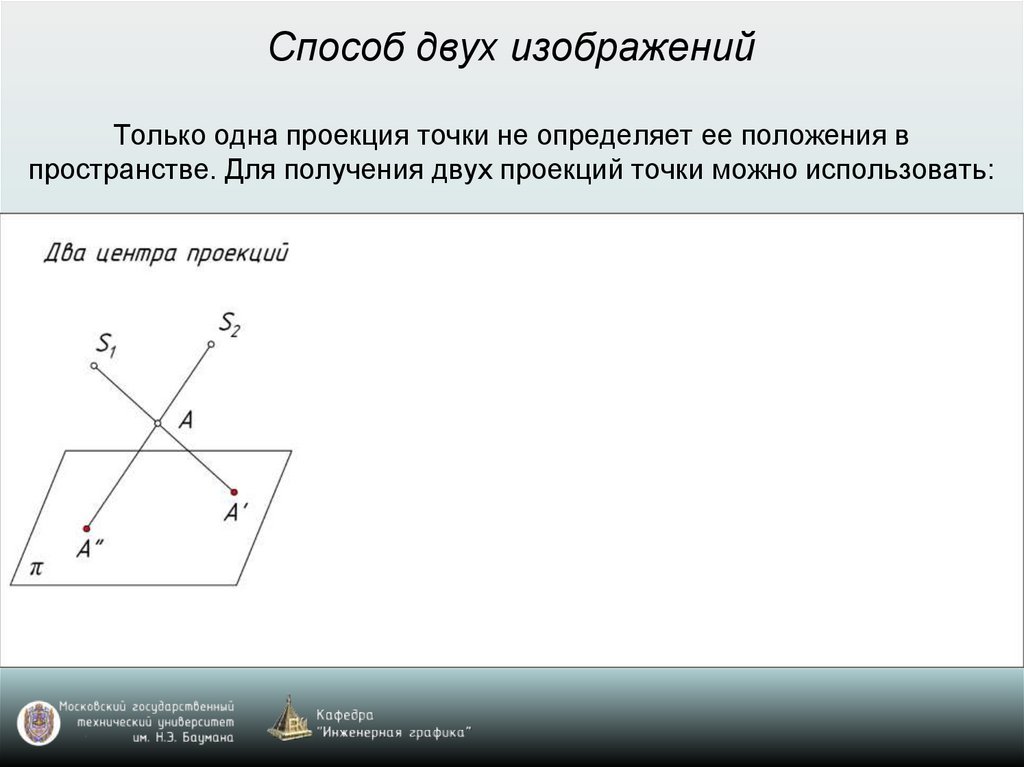
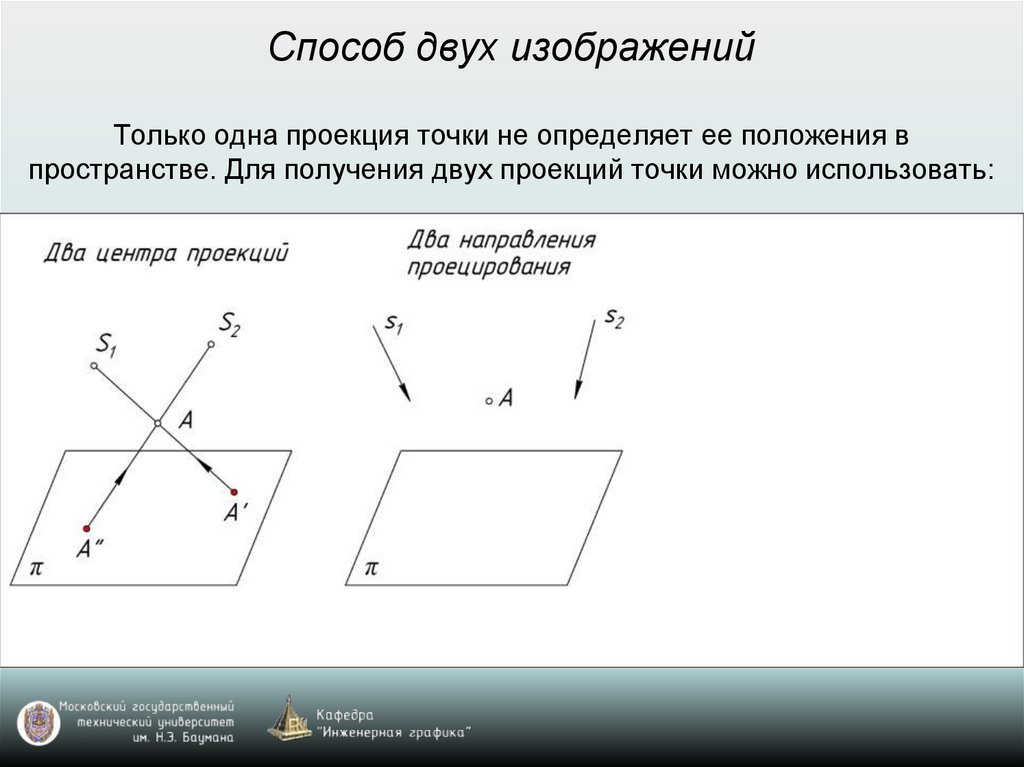
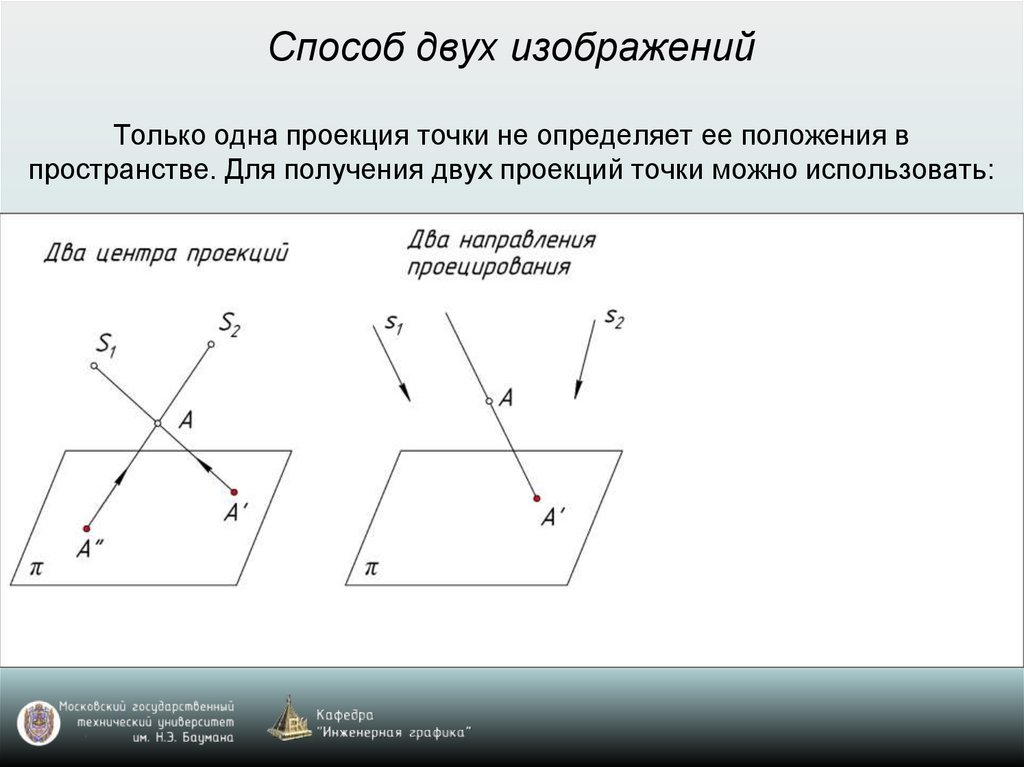
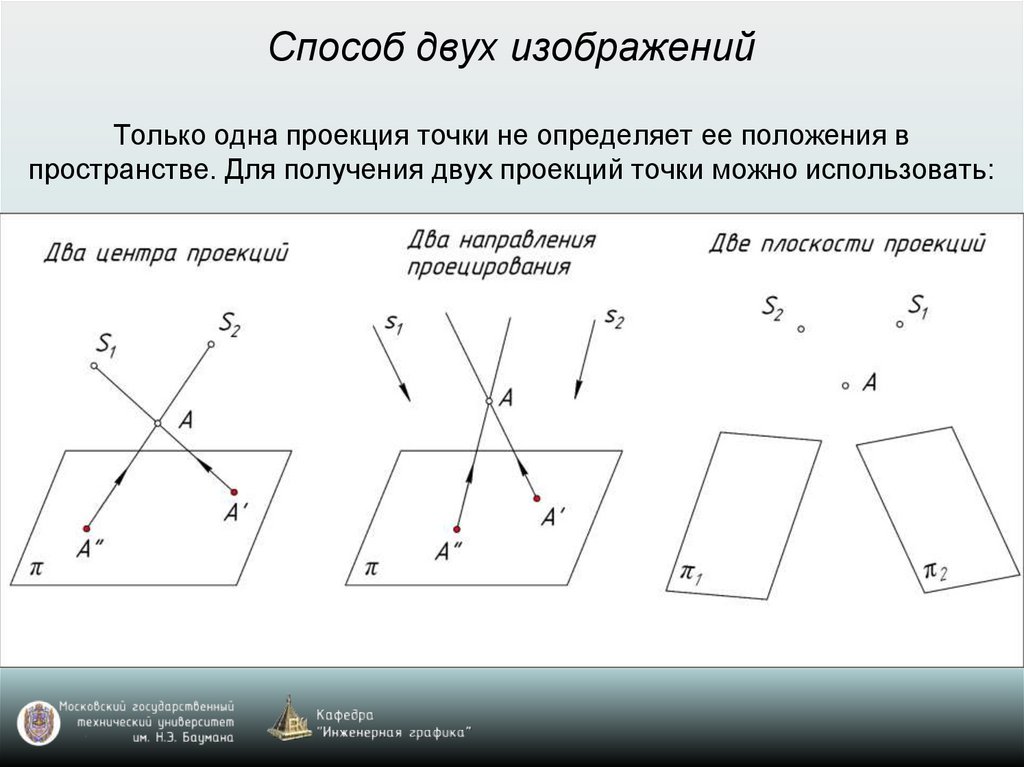
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
18.
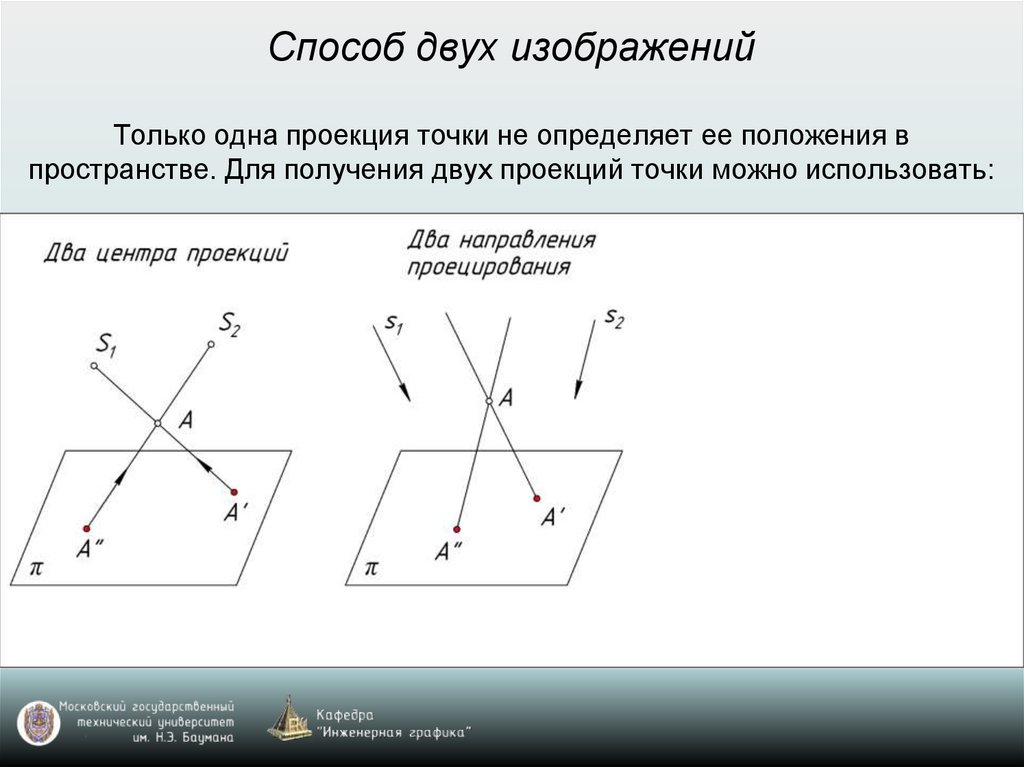
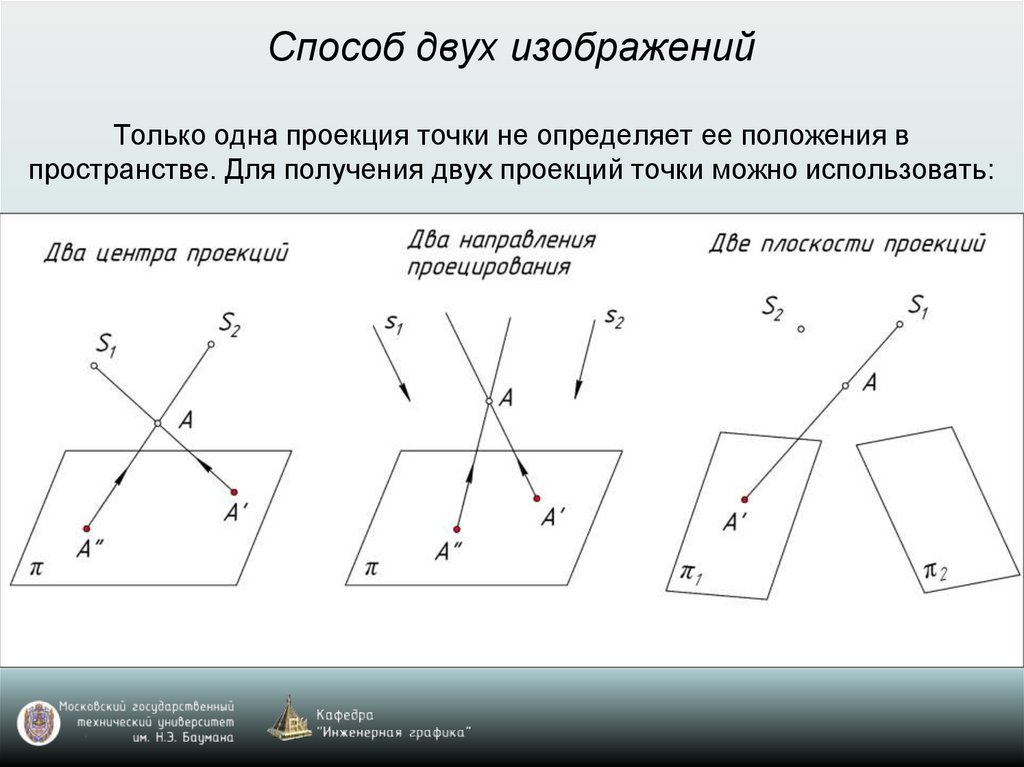
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
19.
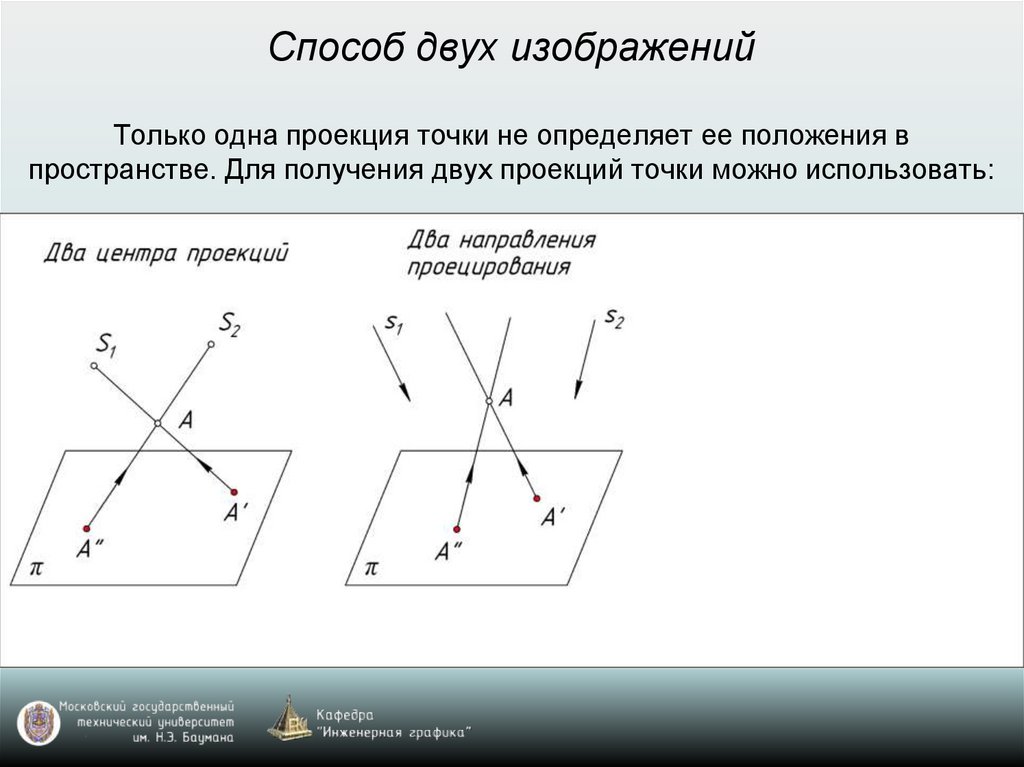
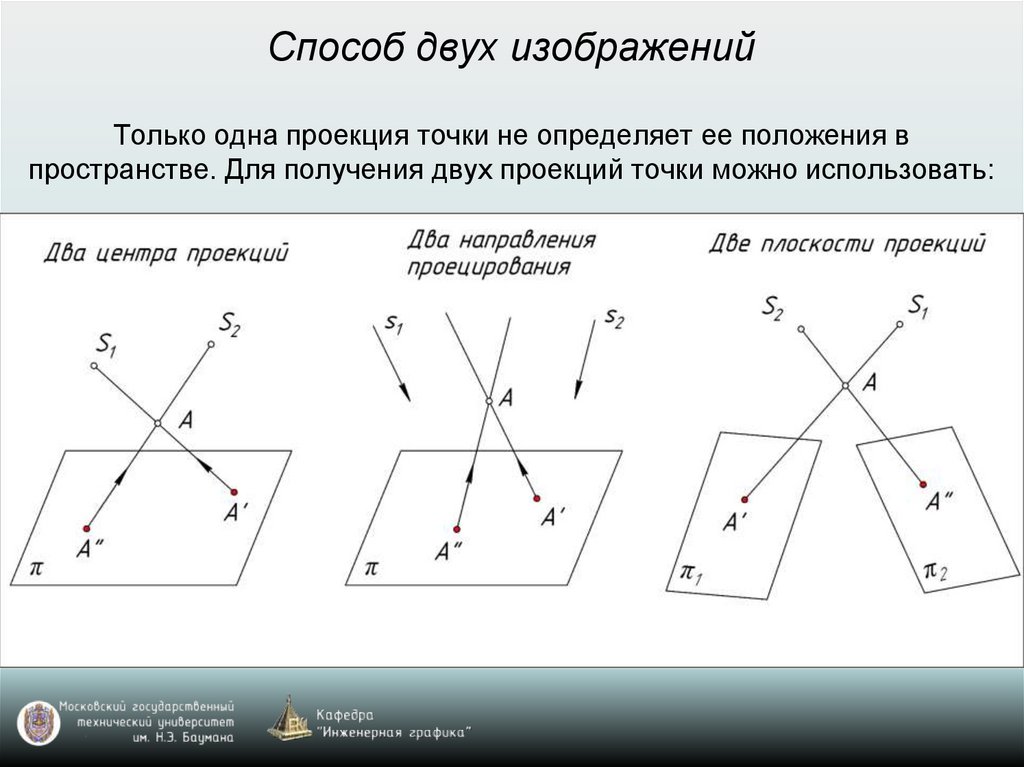
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
20.
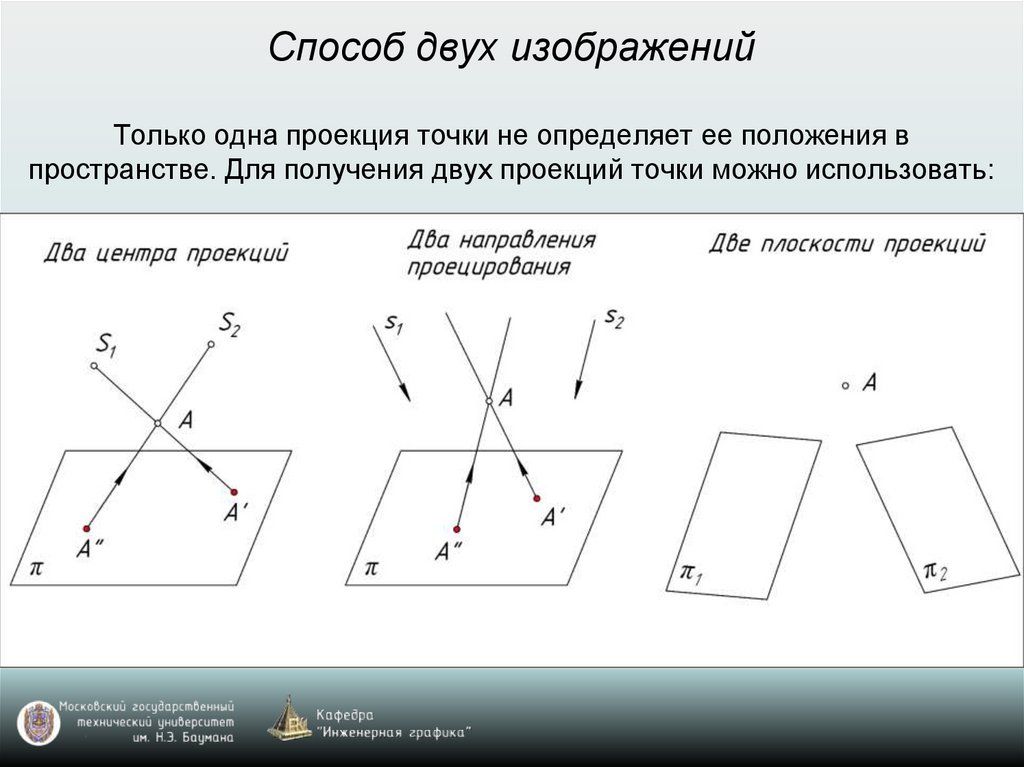
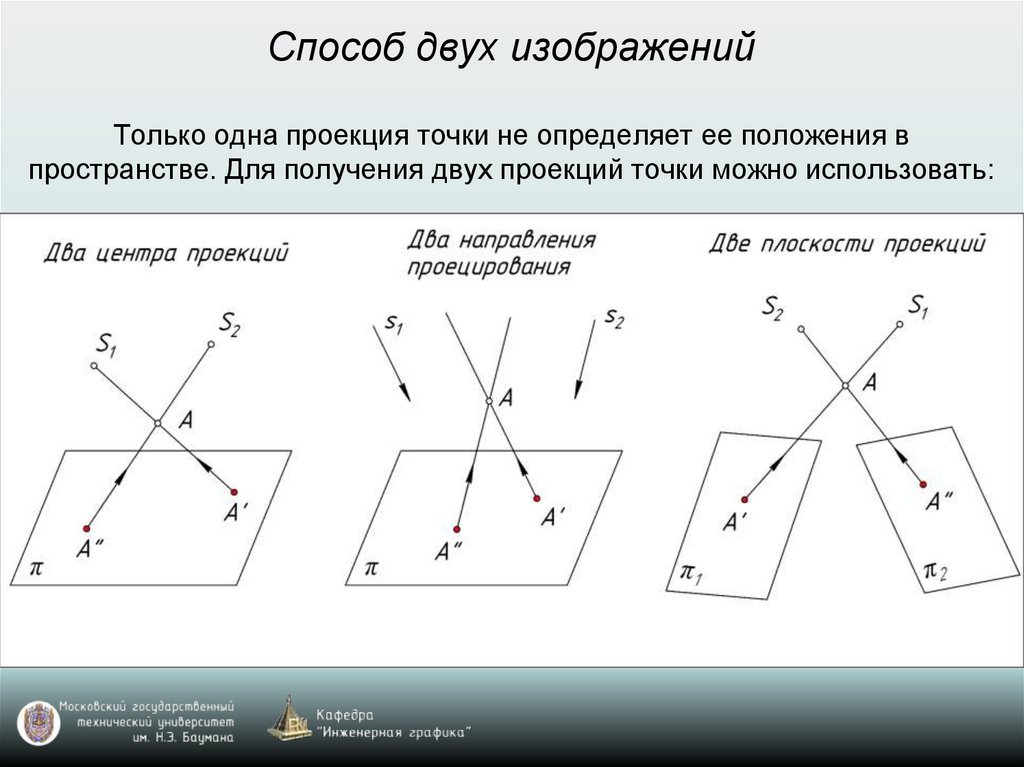
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
21.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
22.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
23.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
24.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
25.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
26.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
27.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
28.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
29.
Способ двух изображенийТолько одна проекция точки не определяет ее положения в
пространстве. Для получения двух проекций точки можно использовать:
30.
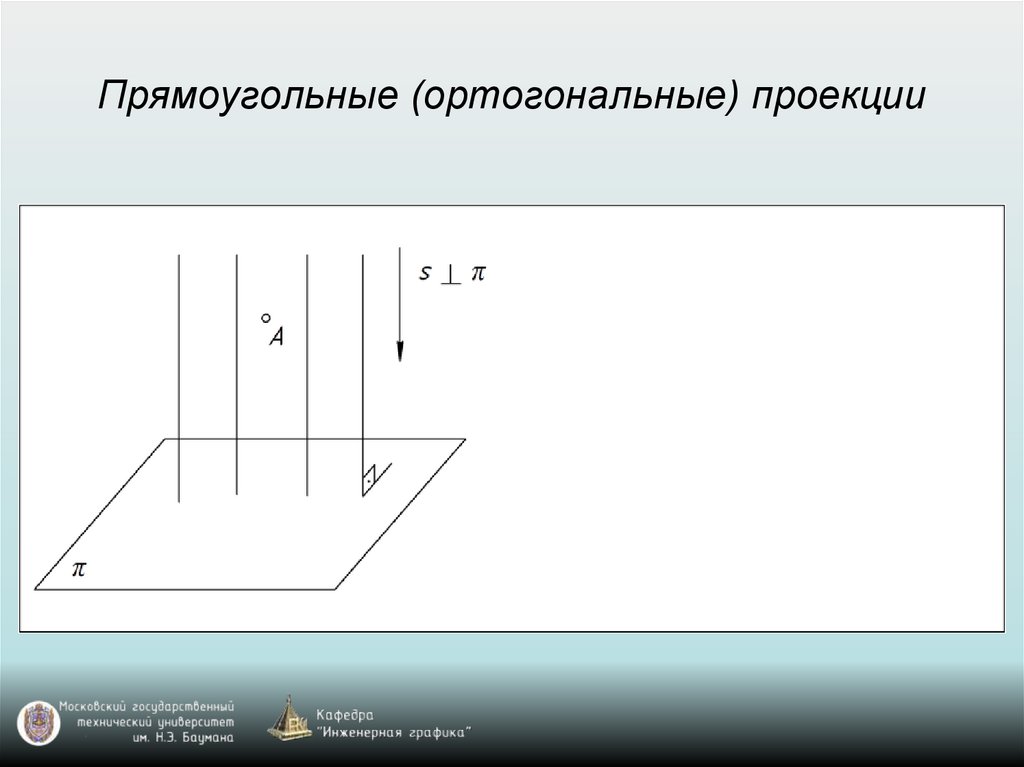
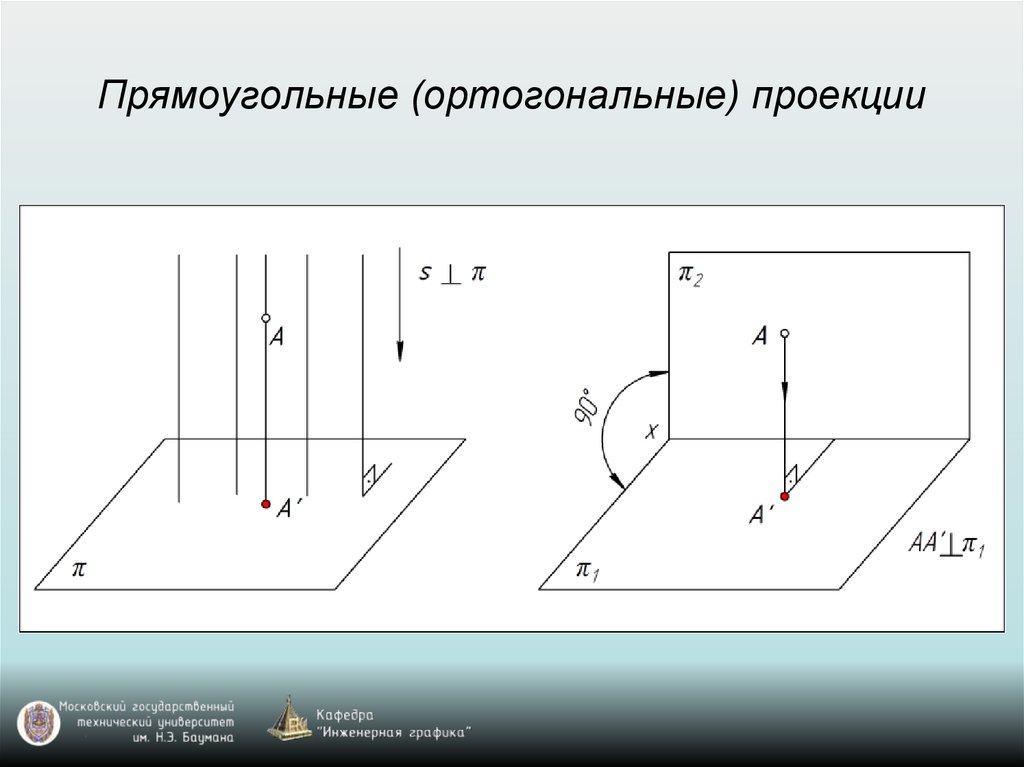
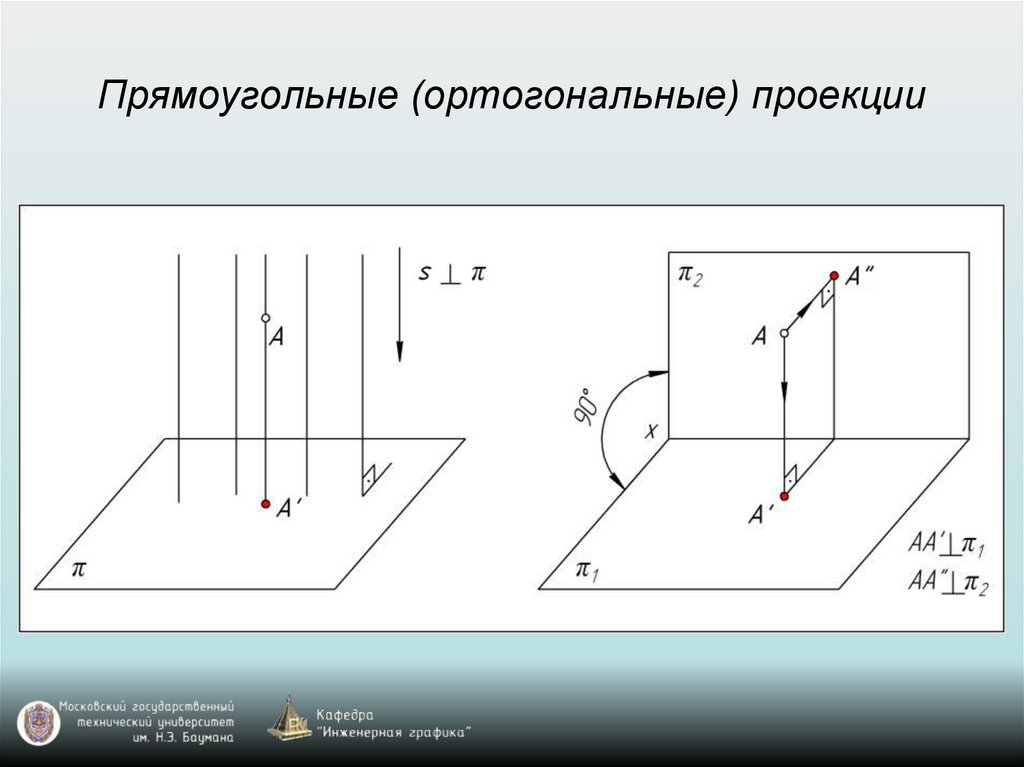
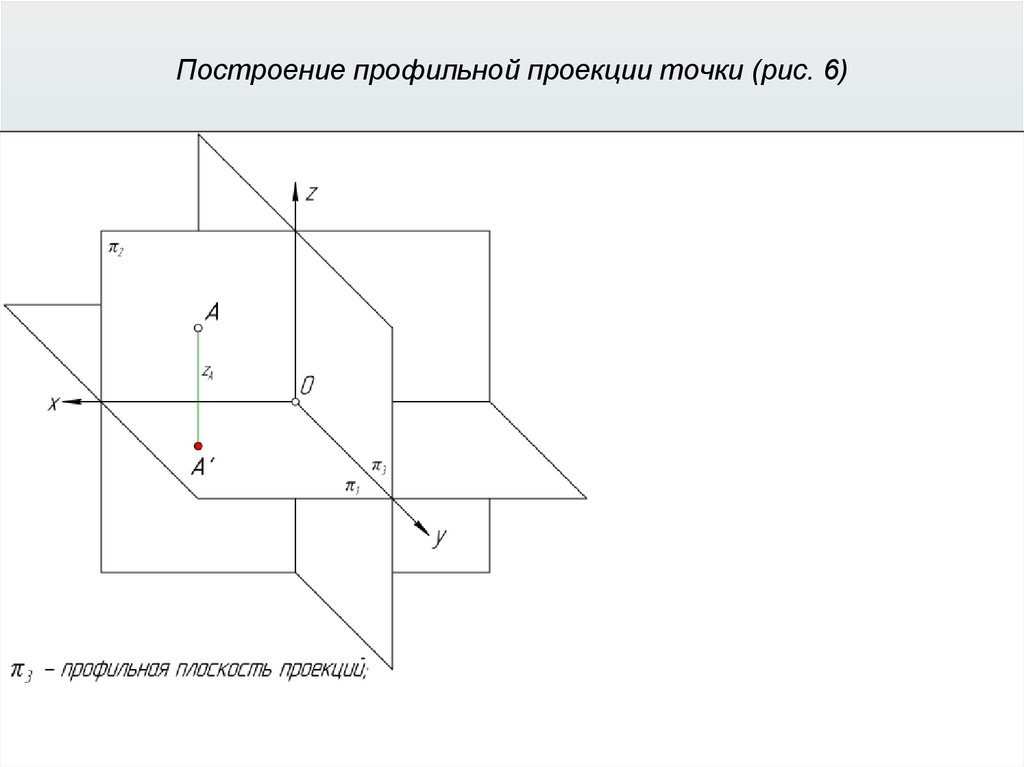
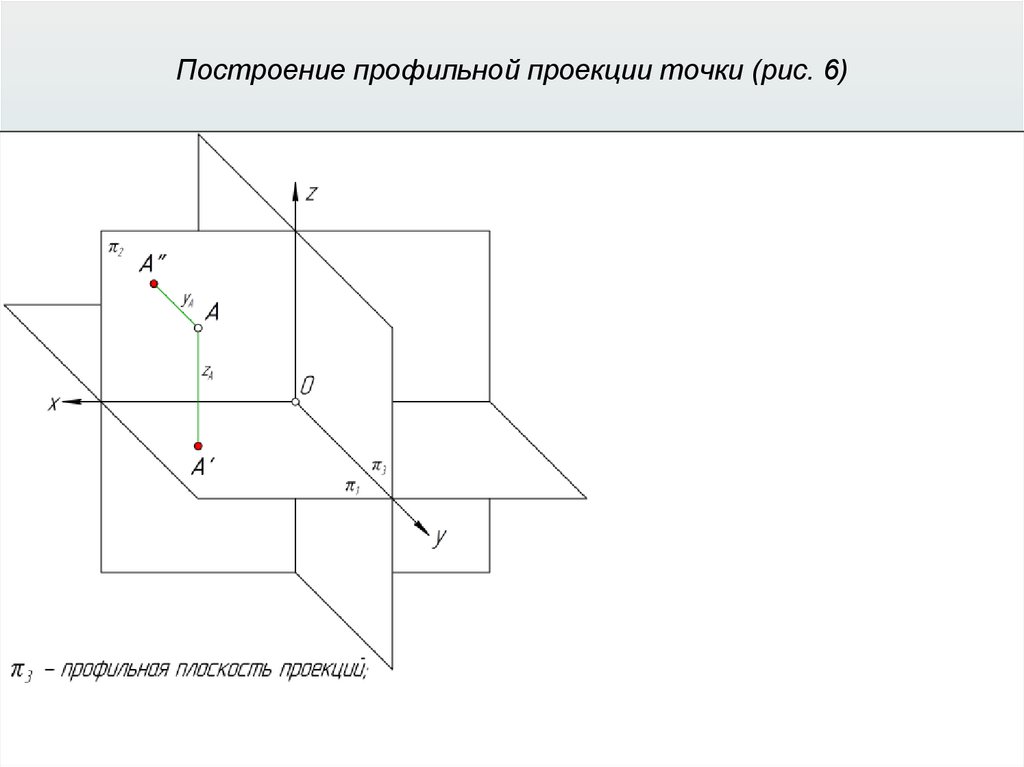
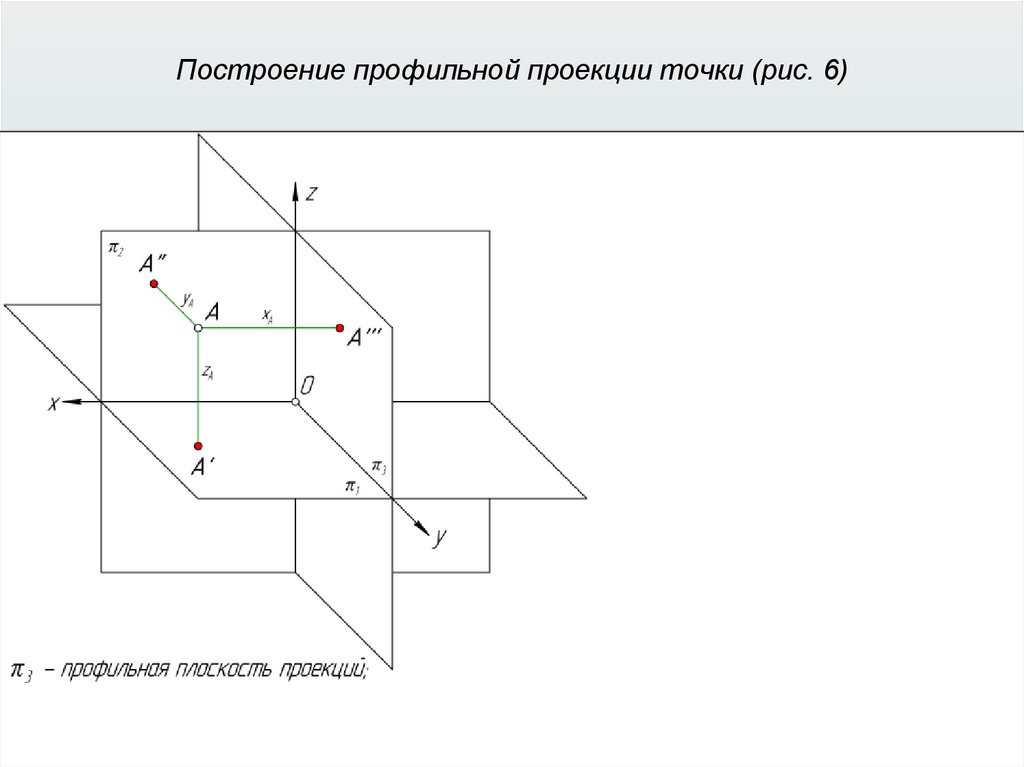
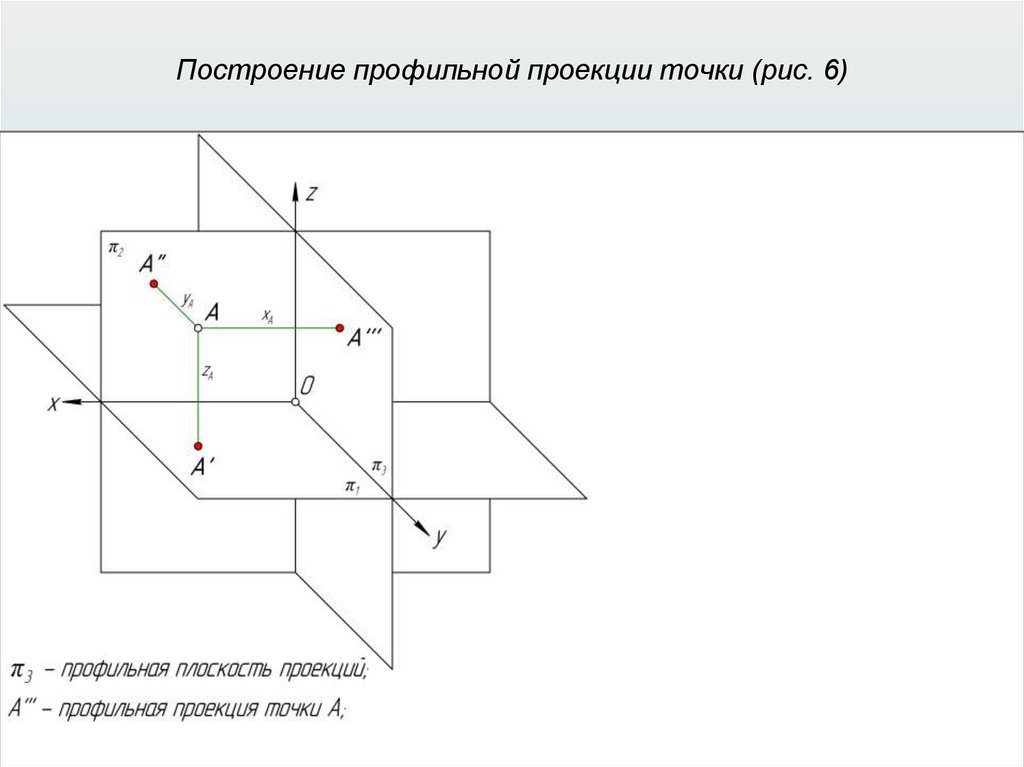
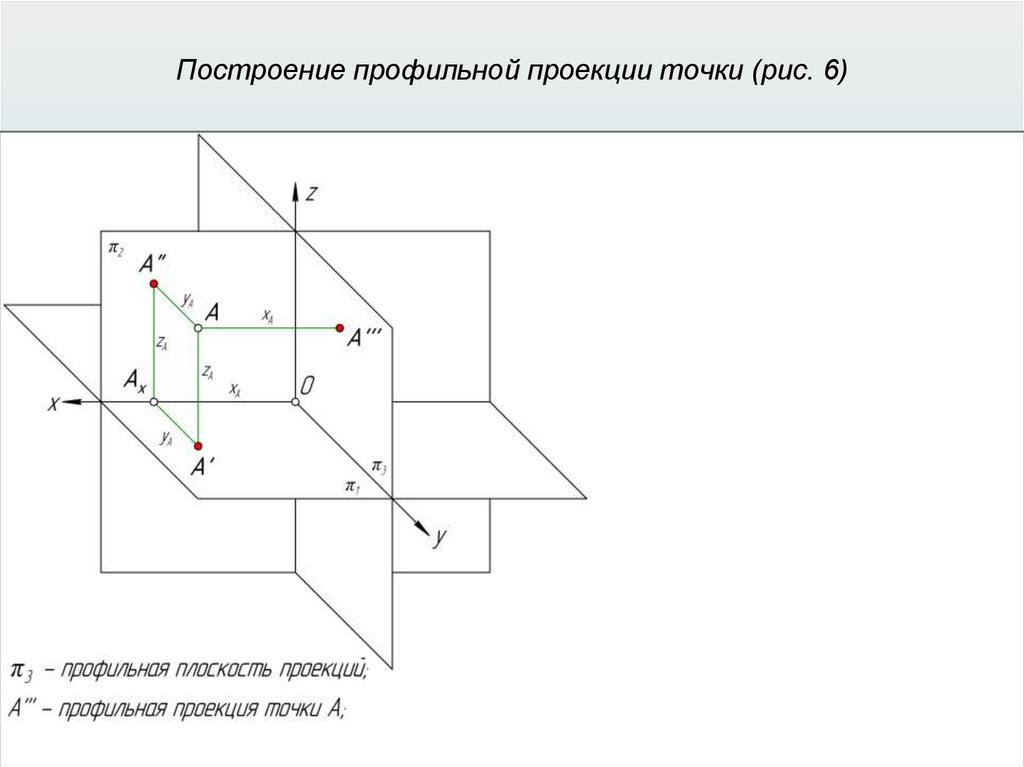
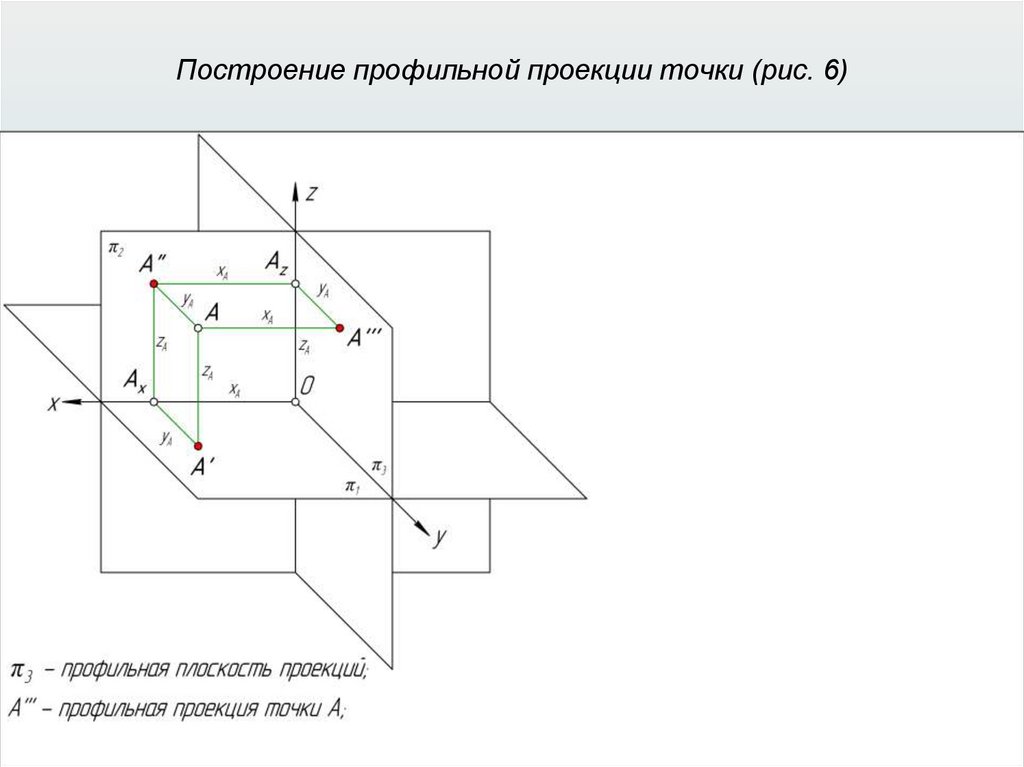
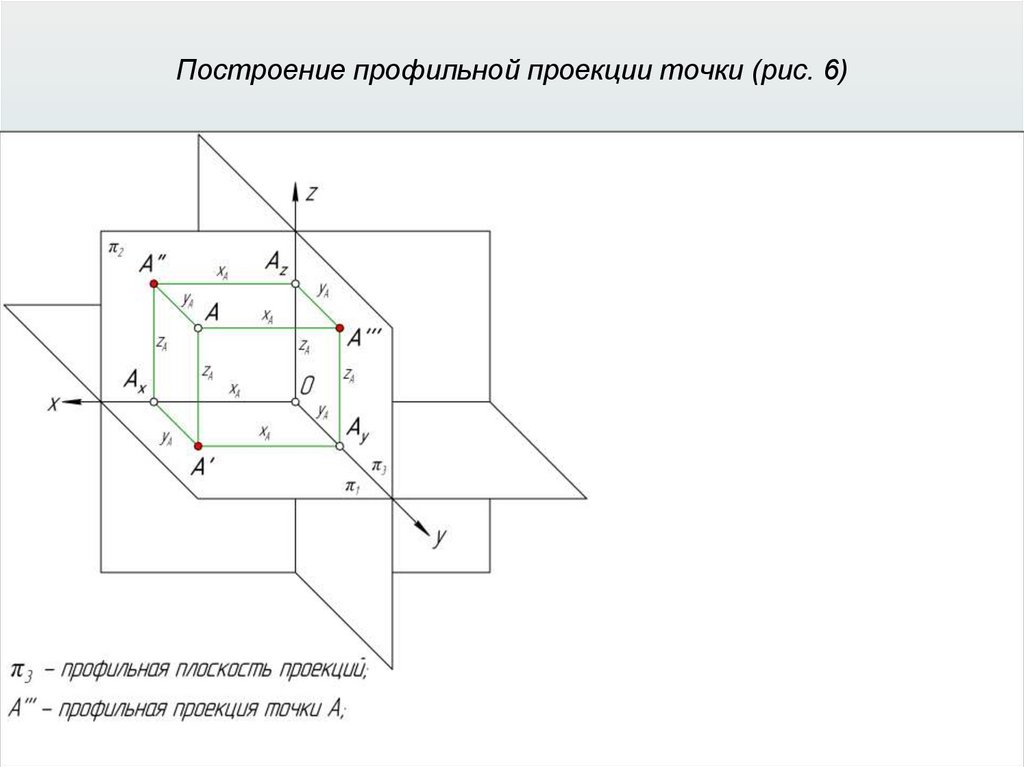
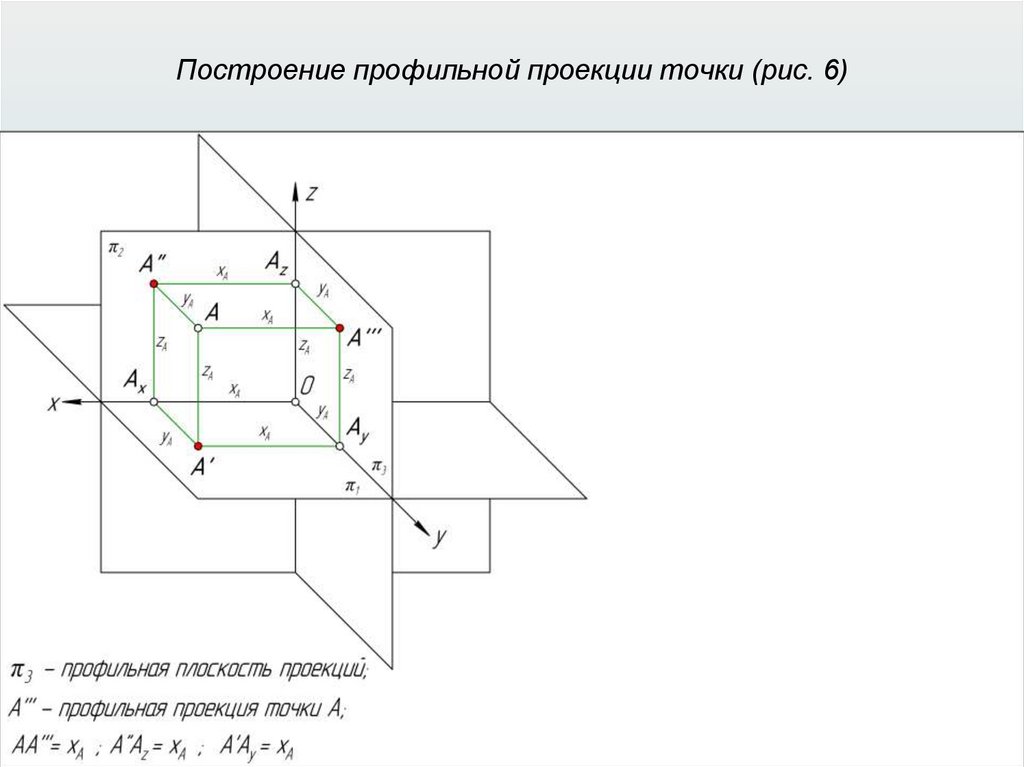
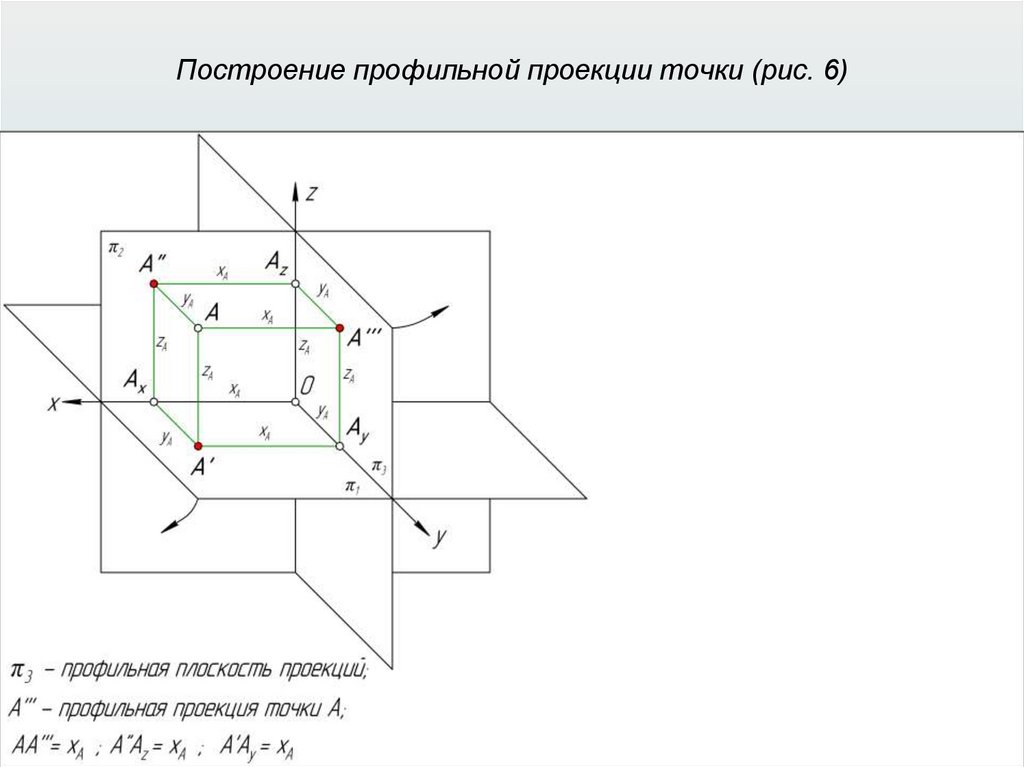
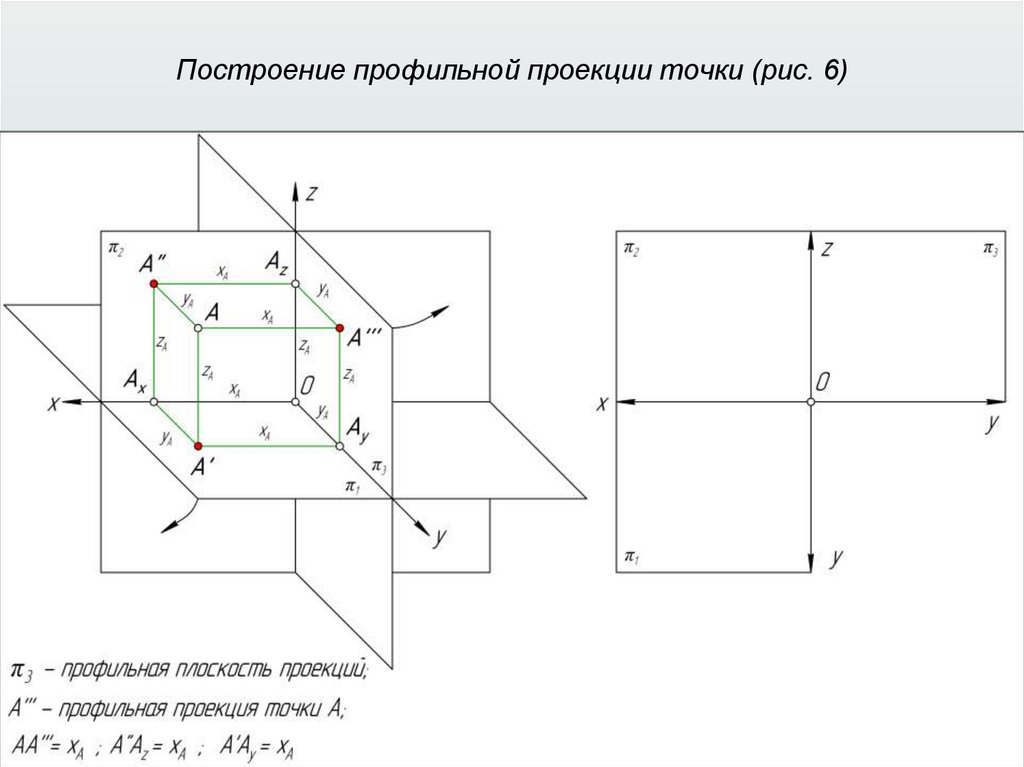
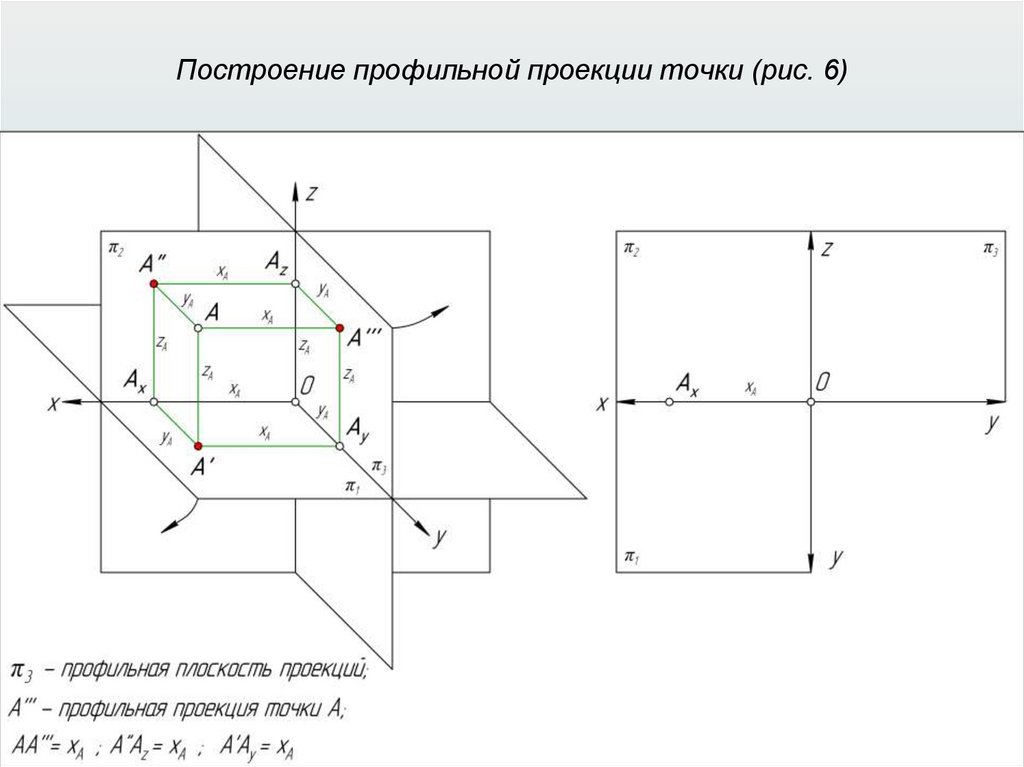
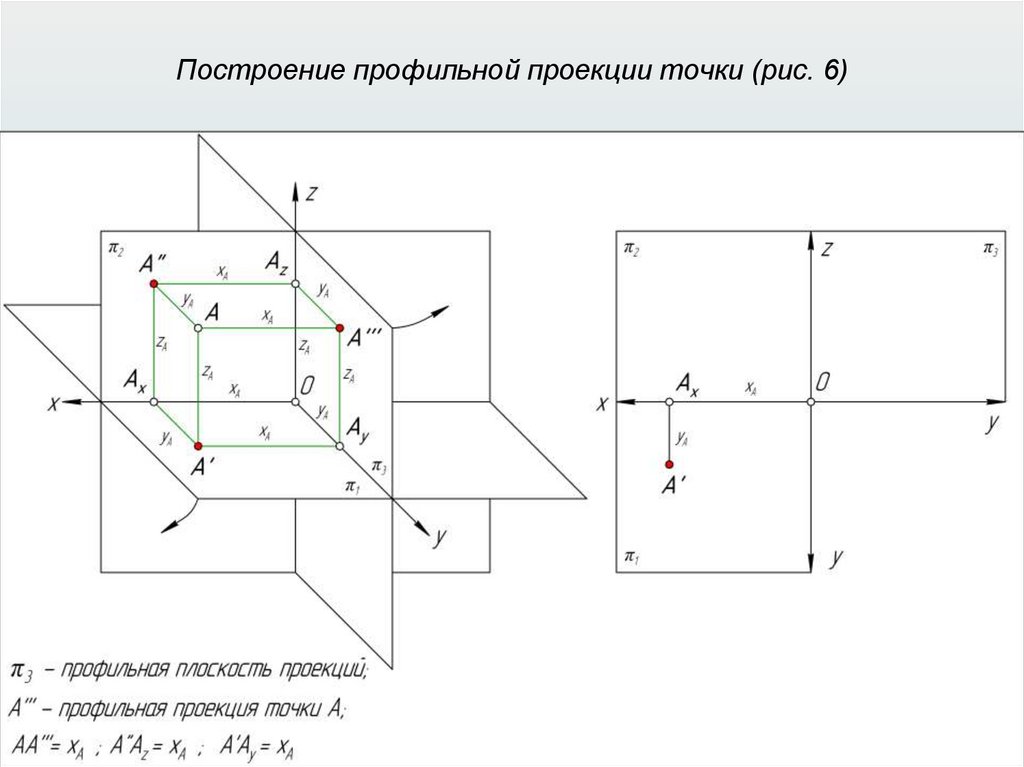
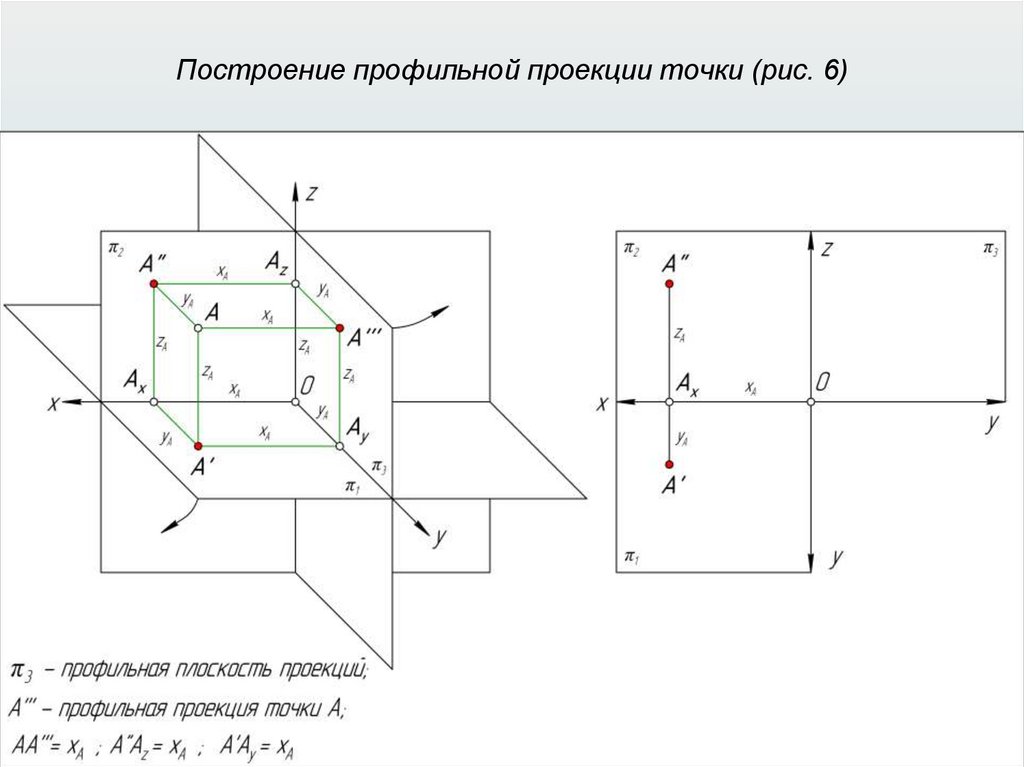
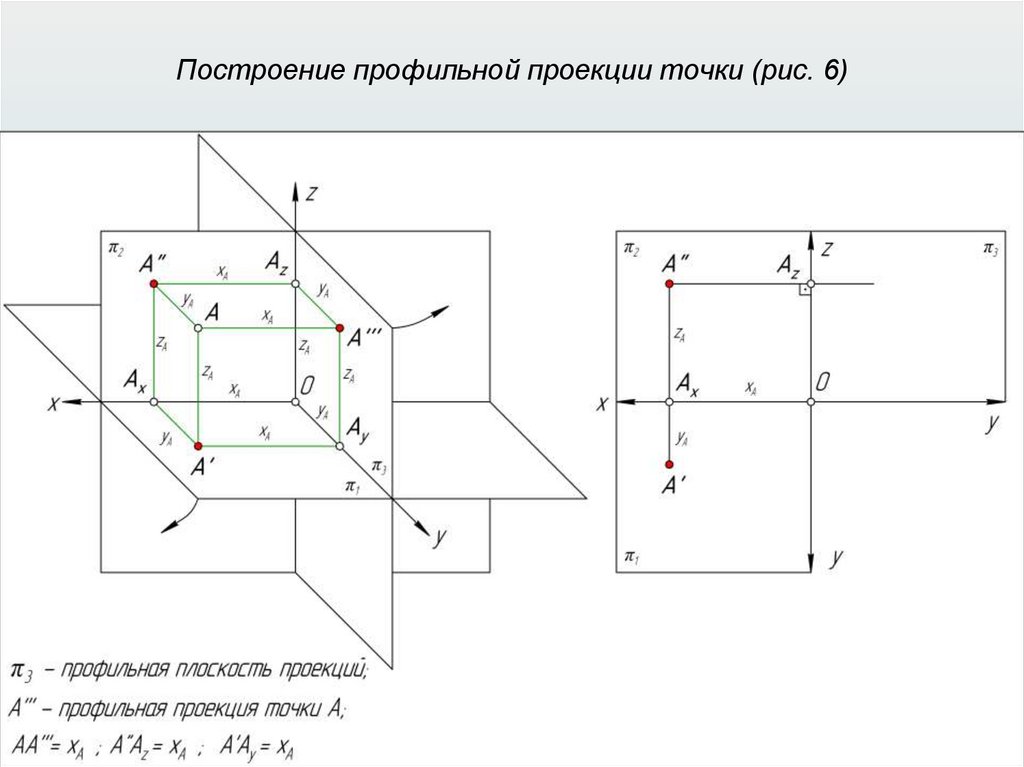
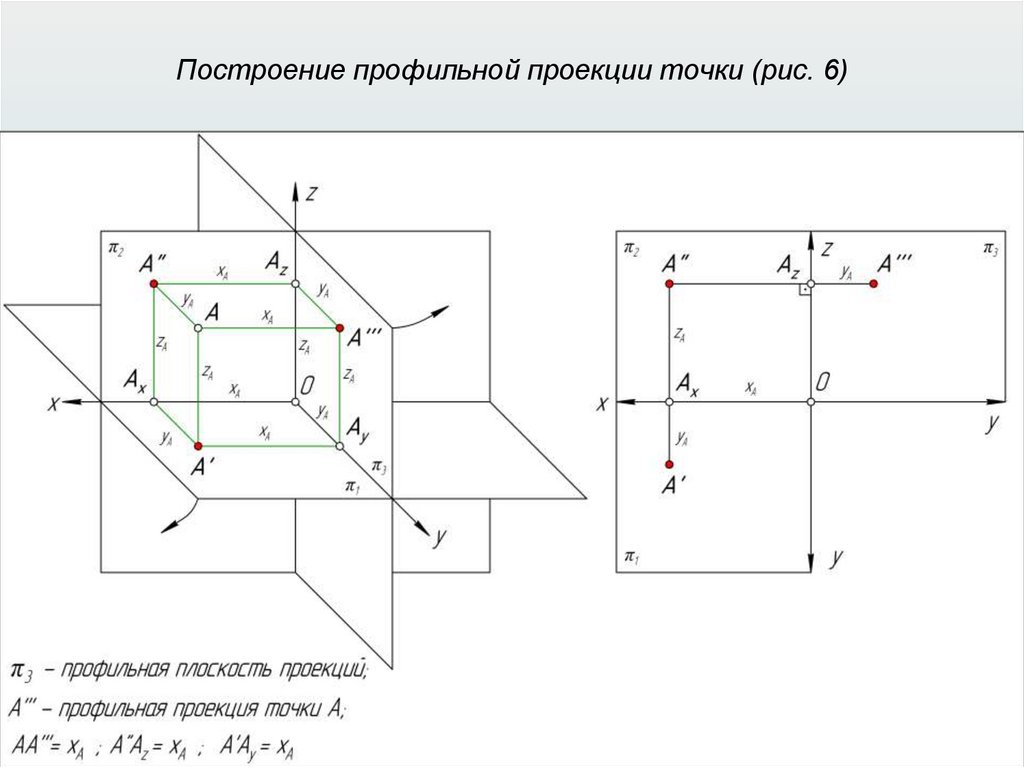
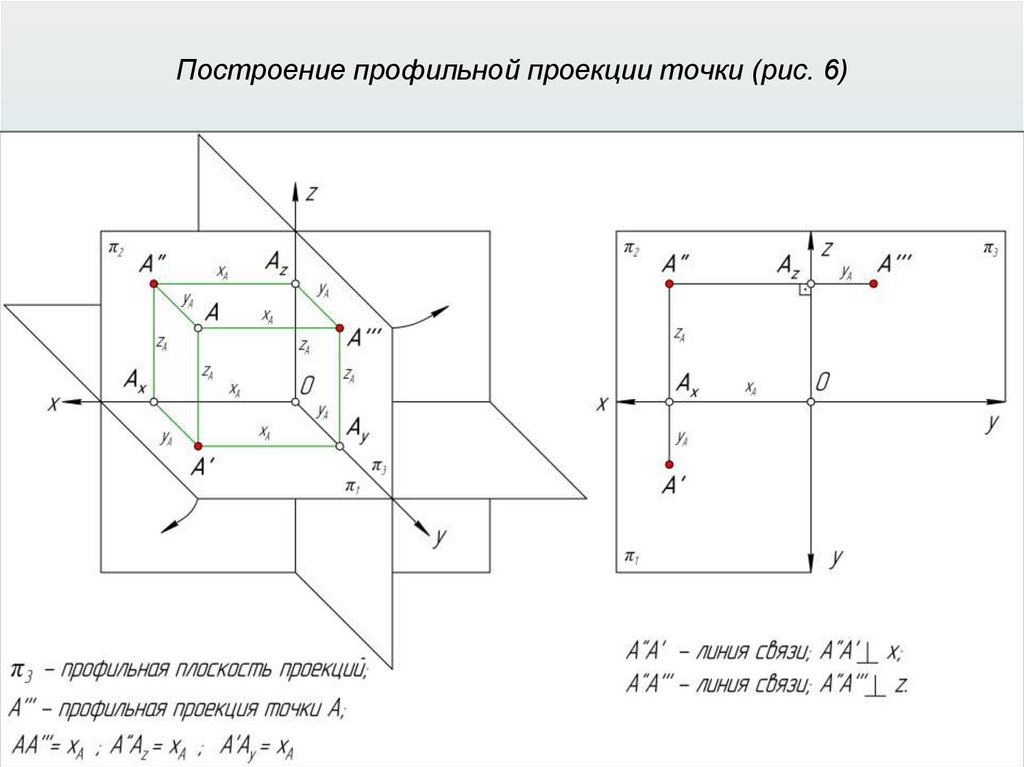
Прямоугольные (ортогональные) проекции31.
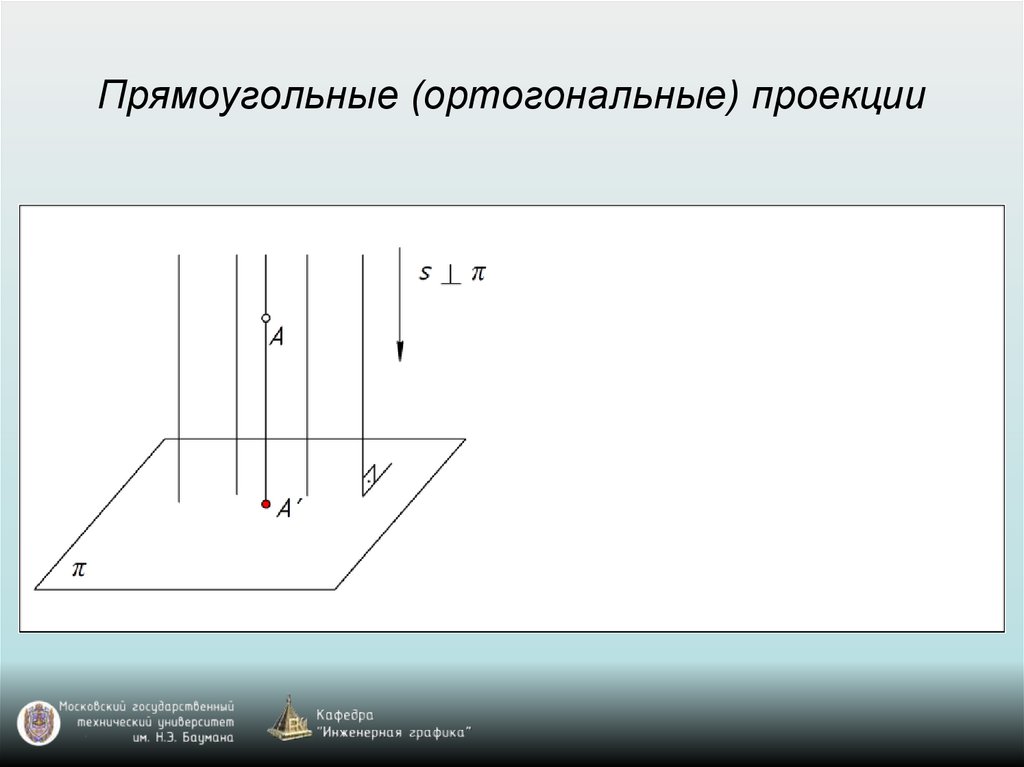
Прямоугольные (ортогональные) проекции32.
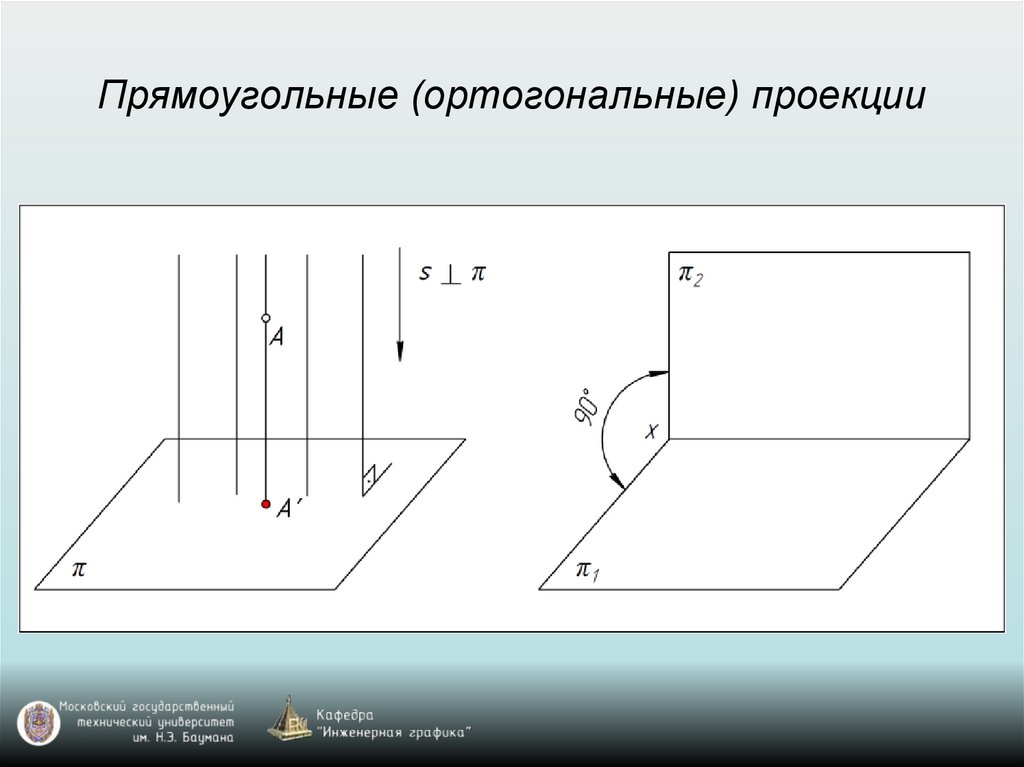
Прямоугольные (ортогональные) проекции33.
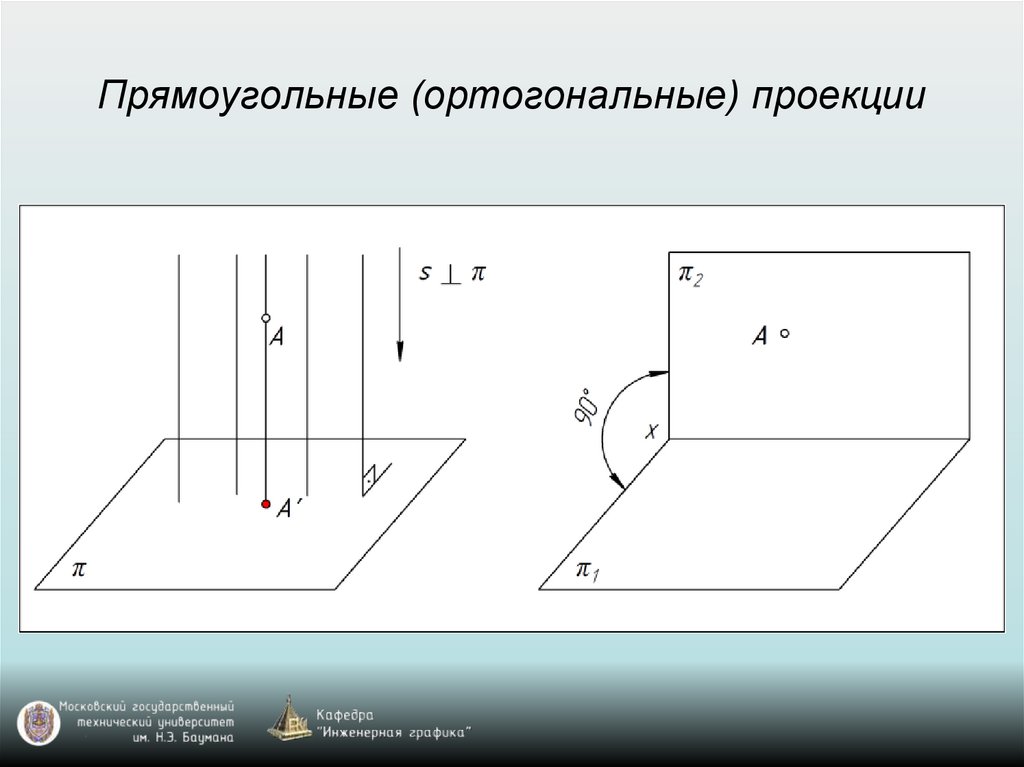
Прямоугольные (ортогональные) проекции34.
Прямоугольные (ортогональные) проекции35.
Прямоугольные (ортогональные) проекции36.
Прямоугольные (ортогональные) проекции37.
Свойства прямоугольного проецирования1. Проекция точки есть точка.
2. В общем случае проекция прямой есть прямая
линия; проекция кривой линии есть кривая.
3. Свойство принадлежности. При проецировании
сохраняется принадлежность точки А линии l:








































 drafting
drafting








