Прямоугольный волновод. Лекция 12

1.

Лекция
Прямоугольный волновод
Учебные вопросы:
• 1. Волны Е - класса в прямоугольном волноводе
• 2. Волны Н - класса в прямоугольном волноводе
3. Анализ волновых процессов в прямоугольном
волноводе

2.

Рязанское гвардейское высшее воздушно-десантное командное училище
Кафедра РУС
Электродинамика и РРВ
Евдокимов Владимир Иванович
кандидат технических наук, доцент

3. Литература:

• 1. Вольман В.И. Пименов Ю.В., Техническая
электродинамика: Учеб. пособие для вузов:– М.: «Связь»,
1971 г. – С.280-288;
• 2. Семенов Н.А. Техническая электродинамика: Учеб.
пособие для вузов:– М.: «Связь», 1973 г. – С.189-202;
• 3. Никольский В.В., Никольская Т.И. Электродинамика
и распространение радиоволн: Учеб. пособие для вузов:–
М.: «Наука», 1989 г. – С.257-267.

4. СВЧ тракты тропосферной станции Р-423

5.

Волновод- устройство или канал в неоднородной
среде, вдоль которого могут распространяться
направленные волны.
Радиоволновод – это элемент радиоэлектронной
аппаратуры, выполненный из хорошо проводящих
материалов (или диэлектрика) и предназначенный
для передачи радиоволн за счет многократного
отражения от стенок волновода

6. В направляющих системах могут распространяться следующие классы волн

ТЕМ -волна
Е-волна
Н-волна

7. 1. Волны Е - класса в прямоугольном волноводе

Анализ процессов в волноводах прямоугольного сечения
производится в декартовой системе координат. Поскольку
поперечные и продольные составляющее электрического поля
связаны друг с другом, то трехмерное уравнение может быть
упрощено :
2 Åz 2 Åz
2
Åz 0
2
2
x
y
y
b
z
ε,μ,σ
а
χ - поперечный волновой коэффициент
(волновое число стоячей волны)
Распространяющаяся волна в
любом направлении является
плоской. Данная система уравнений
решается с учетом граничных
условий для конкретной
направляющей системы.
x

8. Искать решение данного уравнения будем методом разделения переменных

Ez ( õ, ó ) Õ( õ ) Y ( y )
Выполнив преобразования, получаем уравнение:
1 Õ 1 Y
2
2 2 0
X x
Y y
2
2
Удовлетворение данного равенства возможно, если при
произвольных значениях переменных можно записать:
2
1 2Y
1
Õ
2
2 0,
2 2 0
Y y
X x
2 2 2
- уравнение для поперечных волновых коэффициентов,
ξ - поперечный волновой коэффициент по оси ОУ,
η- поперечный волновой коэффициент по оси ОХ,

9. Полученные уравнения можно представить в виде:

y
b
z
Полученные уравнения можно
представить в виде:
ε,μ,σ
2Y
2 Õ
2
2
Y
0
,
Õ 0
2
2
x
y
x
а
Решение этих равнений хорошо известны
Y ( ó ) À sin ó Â cos y ,
Õ( õ ) Ñ sin x D cos x
С учетом граничных условий для прямоугольного волновода
E 0, H n 0
Х(х) = 0 если х = 0 и а; Y(у) у = 0 и в находятся значения
коэффициентов В = 0 и D = 0.
Для дальнейшего выполнения граничных условий можно
потребовать:
â n , n 0,1,2,3... à m , m 0,1,2,3....
n
m
,
â
a
Волновые коэффициенты принимают
дискретные значения и зависят от
геометрических размеров волновода

10.

Составляющее поля для волн Е- класса в прямоугольном
волноводе описываются следующими соотношениями
m
m
n
Ex D
cos
x sin
y
a
a
b
n
m
n
E y D
sin
x cos
y
b
a
b
2
2
m
j t Z
n
m
n
e
Åz jD
x sin
y
sin
b
a
b
a
n
m
n
H x D a
sin
x cos
y
b
a
b
m
m
n
H y D a
cos
x sin
y
a
a
b
1
D Åmz 2
k 2
n 0 ,1,2,3...
m 0,1,2 ,3....
10

11.

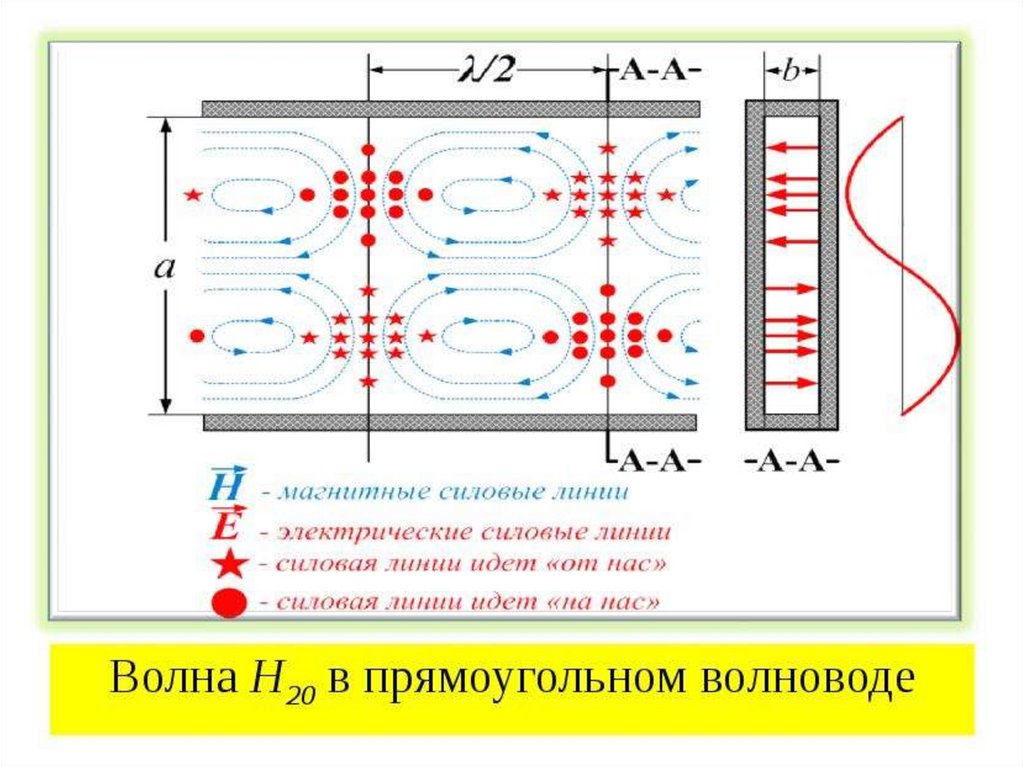
Полученные соотношения позволяют графически
представить распределение полей в прямоугольном
волноводе.
Для обозначения каждого конкретного типа волны в
прямоугольном волноводе применяют два цифровых
индекса, которые ставятся у буквы, обозначающей класс
волны
Е11, Н10
Первая цифра характеризует количество полуволн
электромагнитного поля, укладывающихся вдоль
широкой стенки волновода (если изменения поля нет, т. е. оно
постоянно, то индекс — нуль, изменение на полпериода — индекс 1,
изменение на полный период — индекс 2 и т. д.).
Второй индекс характеризует изменение поля вдоль
узкой стенки волновода.

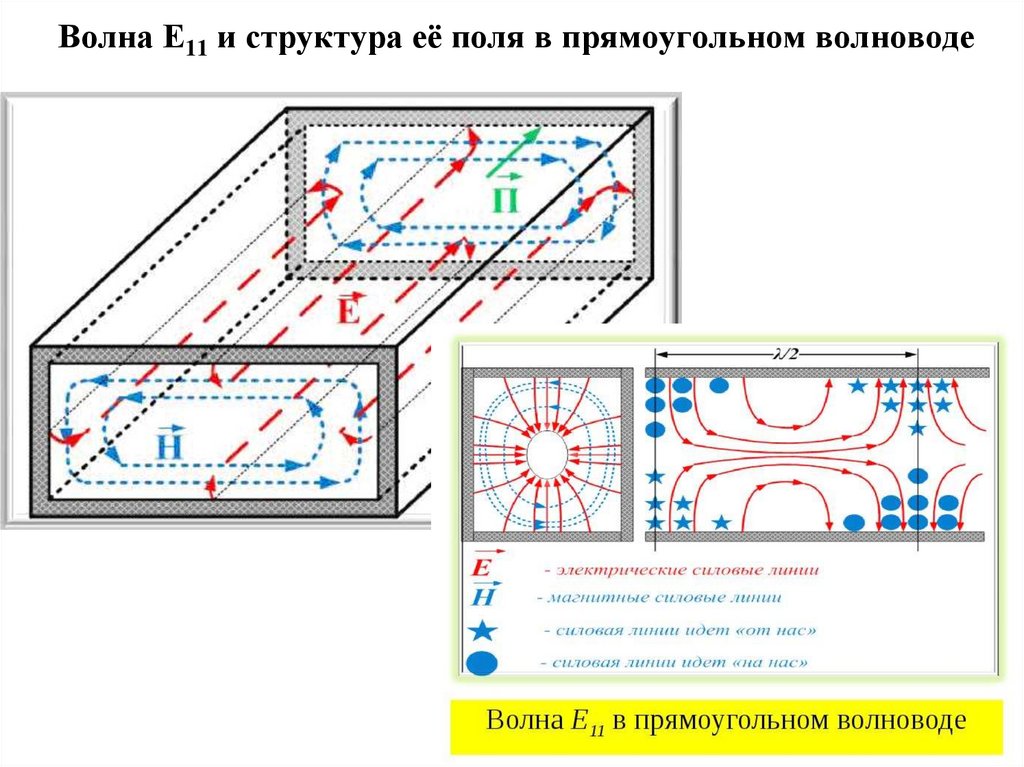
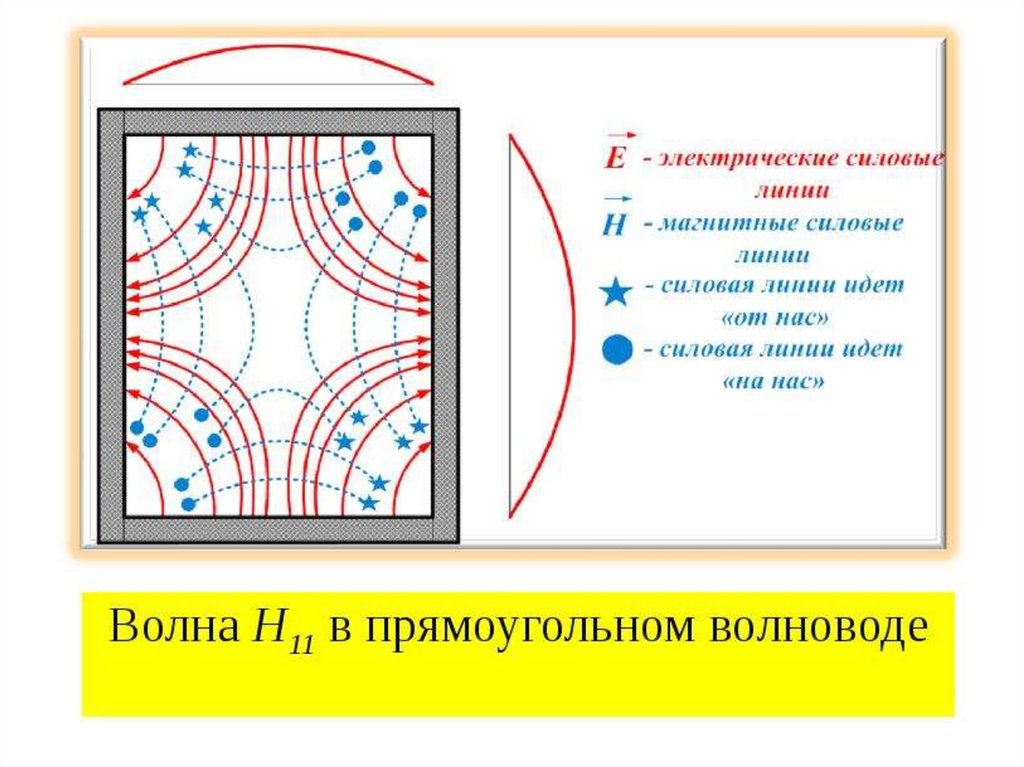
12. Волна Е11 и структура её поля в прямоугольном волноводе

13. Искать решение данного уравнения будем методом разделения переменных

2. Волны Н - класса в прямоугольном волноводе
Анализ процессов для Н- волны в прямоугольном волноводе
осуществляется с помощью соотношения :
2Í z 2Í z
2
2
(
k
)Í z 0
2
2
x
y
Искать решение данного уравнения будем методом
разделения переменных
Í z ( õ, ó ) Õ( õ ) Y ( y )
Выполнив преобразования, получаем уравнение:
1 2 Õ 1 2Y
2
2 2 0
X x
Y y
Удовлетворение данного равенства возможно, если при
произвольных значениях переменных можно записать:
2 2 2
2
1 2Y
1
Õ
2
2 0,
2 2 0
Y y
X x
- уравнение для поперечных волновых коэффициентов,
ξ - поперечный волновой коэффициент по оси ОУ,
η- поперечный волновой коэффициент по оси ОХ,

14. Полученные уравнения можно представить в виде:

y
b
z
Полученные уравнения можно
представить в виде:
ε,μ,σ
2Y
2 Õ
2
2
Y
0
,
Õ 0
2
2
x
y
x
а
Решение этих равнений хорошо известны
Y ( ó ) À sin ó Â cos y ,
Õ( õ ) Ñ sin x D cos x
Поперечные составляющее вектора Е в прямоугольном
волноводе связаны с Нz соотношениями:
Í z
Ex
0 ïðè õ 0,à
x
Ez
Ey
0 ïðè ó 0,â
y
С учетом граничных условий для касательной составляющей
Еτ находятся значения коэффициентов А=0 и С=0.

15.

Для дальнейшего выполнения граничных условий поперечные
коэффициенты должны описываться выражениями:
â n , n 0,1,2,3... à m , m 0,1,2,3....
n
m
,
â
a
Следовательно, для Е и Н – волн выражения для
поперечных волновых коэффициентов, критических частот и
критических длин волн одинаковы.
Таким образом, продольная составляющая Нz должна
описываться выражением:
H z Í mz cos ó cos õ e
j t z
15

16.

С учетом выполнения граничных условий все составляющие
поля для волн Н-класса в прямоугольном волноводе могут быть
представлены следующими выражениями:
D jD1
m m n
E x D
cos
x sin
y
a
a b
1
k 2 2
n 0 ,1,2 ,3...
m
0
,
1
,
2
,
3
..
n m n
E y D sin
x cos
y
b
a b
1 m m n
H x D
sin
x cos
y
a a
a
b
1 n m n
H y D
cos
x sin
y
a b
a b
2
2
1 m n m n
H z jD
x cos
y
cos
a a b a b

17. Волна Н10 и структура её поля в прямоугольном волноводе

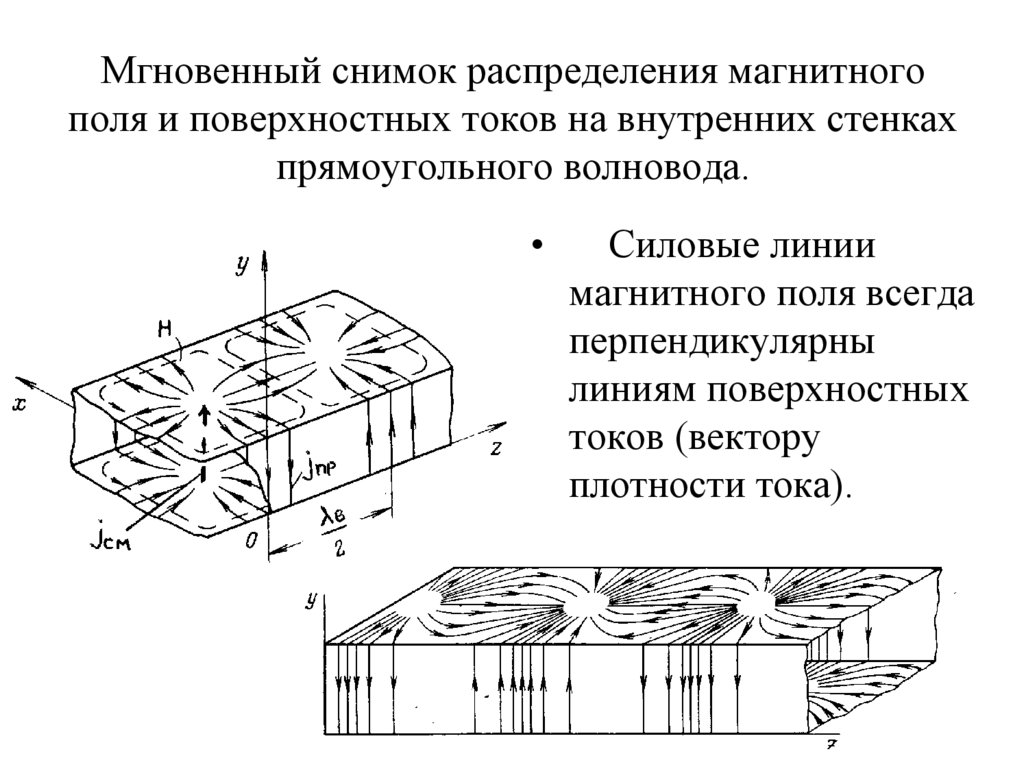
18. Мгновенный снимок распределения магнитного поля и поверхностных токов на внутренних стенках прямоугольного волновода.

Силовые линии
магнитного поля всегда
перпендикулярны
линиям поверхностных
токов (вектору
плотности тока).

19.

20.

21.

3. Анализ волновых процессов в
прямоугольном волноводе
1. В прямоугольном волноводе может распространяться
бесконечное множество электромагнитных полей Е и
Н классов, структура которых определяется значениями
чисел n и m.
• 2. Составляющие поля Е┴ и Н┴ отстают по фазе на 900
( т.е. сдвинуты в пространстве на λ/4) от продольных
составляющих Еz и Нz.
• Поперечные составляющие поля Е┴ и Н┴ синфазны,
перпендикулярны и пропорциональны друг – другу.

22.

3. В прямоугольных волноводах плоская однородная
ЭМВ распространяется зигзагообразно, многократно
отражаясь от поперечных стенок этого волновода
(концепция парциальных волн).
Суперпозиция парциальных волн, удовлетворяющих
граничным условиям на внутренних стенках волновода,
образует поперечные стоячие волны и бегущие вдоль
оси Z.

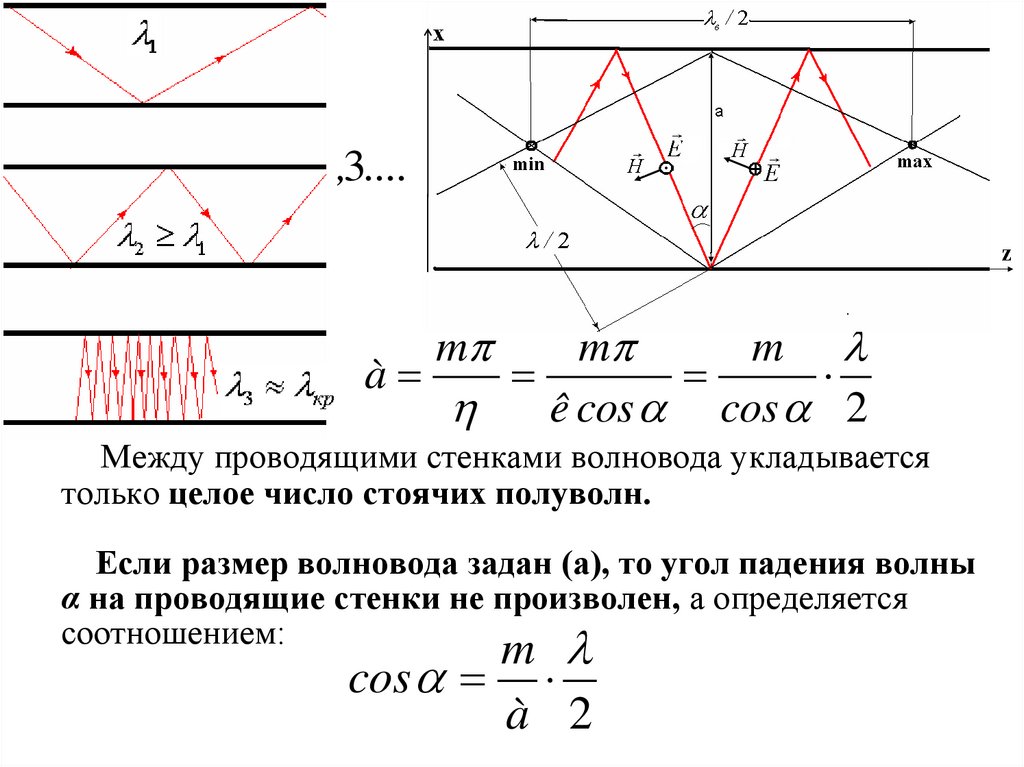
23. Между проводящими стенками волновода укладывается только целое число стоячих полуволн. Если размер волновода задан (а), то угол

à m , m 0,1,2,3....
m
m
m
à
ê cos cos 2
Между проводящими стенками волновода укладывается
только целое число стоячих полуволн.
Если размер волновода задан (а), то угол падения волны
α на проводящие стенки не произволен, а определяется
соотношением:
m
cos
à 2

24.

4. В любой точке фронта плоской волны фаза
электрического и магнитного полей перемещается с фазовой
скоростью vф, превышающей скорость света
vô ñ / sin
5. Групповая скорость в волноводах vГР равна скорости
перемещения вдоль оси волновода высокочастотной
энергии, связанной с волной, и определяется значениями
меньше скорости света
vãð ñ sin

25.

6. Фазовая и групповая скорость в прямоугольном
волноводе связаны с критической частотой (длиной волны)
Vф
c
f кр
1
f0
0
f кр
c 1
Vг р c 1
f
0
кр
2
2
2
Зависимость фазовой скорости и длины волны в волноводе
от частоты называется дисперсией.

26.

7. Критической длиной волны называется такая длина
волны, измеренная в свободном пространстве, а не волноводе,
при которой прекращается передача энергии и распространение
волны по волноводу.
Значение критической длины волны определяется
размерами волновода (а и в) и значениями чисел n и m.
2
n
m
2
2
2
,
кр
2
2
â
a
êð
2
m2 n2
2
2
a
b
f êð
ñ
2
2
2
m n
2
2
a
b
8. В волноводе смогут распространяться и переносить
энергию только волны, для которых λ < λкр

27.

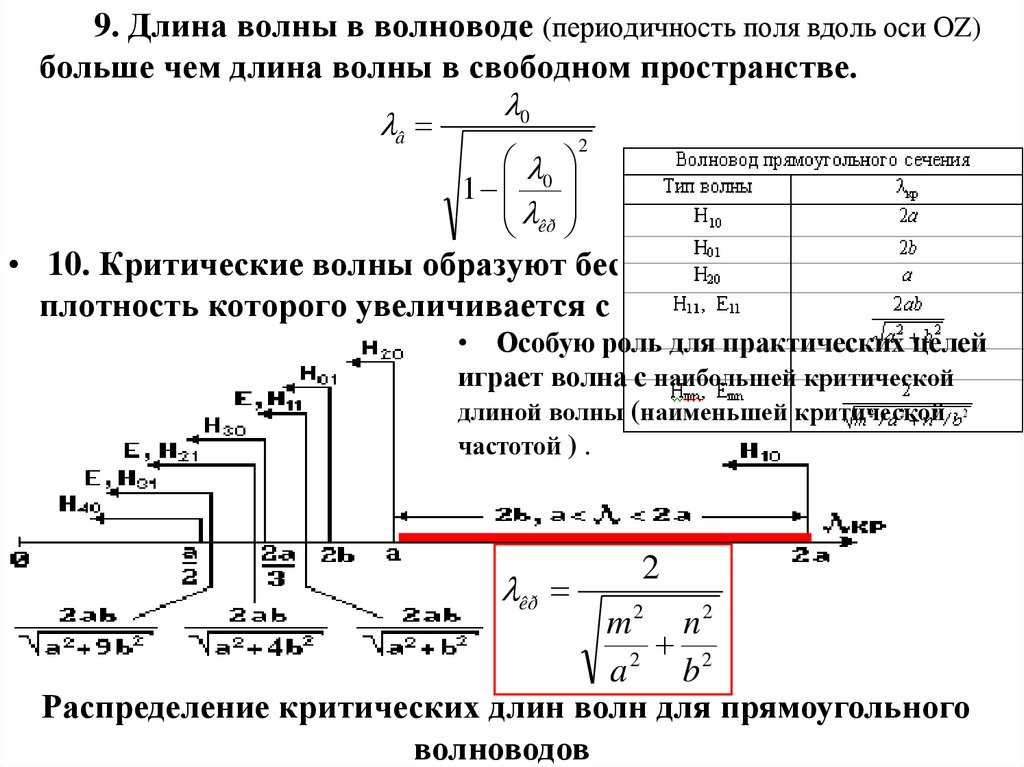
9. Длина волны в волноводе (периодичность поля вдоль оси ОZ)
больше чем длина волны в свободном пространстве.
0
â
2
0
1
êð
• 10. Критические волны образуют бесконечный спектр,
плотность которого увеличивается с ростом m и n.
• Особую роль для практических целей
играет волна с наибольшей критической
длиной волны (наименьшей критической
частотой ) .
êð
2
m2 n2
2
2
a
b
Распределение критических длин волн для прямоугольного
волноводов

28.

11. Наиболее часто для передачи СВЧ энергии по
прямоугольному волноводу применяют основную волну типа
Н10,
12. Волны высших порядков не находят практического
применения, т.к. для их передачи необходимо увеличивать
сечение волновода и потери энергии при этих волнах
увеличиваются.
13. Предельная мощность основной волны
прямоугольного волновода определяется соотношением:
2
f êð
1
àâ
f 2
Ðïðåä
Åïðîá
4
Zâ
Епроб= 30 кВ/см

29. 14.Выбор размеров прямоугольных волноводов

Общее условие существования только основной волны
можно сформулировать так: рабочая длина волны должна
быть меньше критической длины волны основного типа,
но больше критической длины волны ближайшего
высшего типа.
Для волновода прямоугольного сечения с волной λкр
должны выполнятся следующие неравенства:
λкр/2< а < λкр,
в < λкр/2
Обычно размер широкой стенки волновода выбирают
равным примерно а ≈ 0.7 λкр.
Размер узкой стенки волновода b определяет пробивную
прочность и потери в стенках волновода. Обычно его
выбирают равным b = (0,4-0,5)а.
Если потери не имеют большого значения, а передаваемая
мощность невелика, то можно использовать «узкие»
волноводы, для которых b/а = 0.1…0.2