Электромагнитные колебания в полых резонаторах. Лекция 12

1. Лекция №12. Электромагнитные колебания в полых резонаторах.

1. Электромагнитные колебания в объемных
резонаторах.
2. Поля в полых прямоугольных и круглых
резонаторах.
3. Добротность объемных закрытых резонаторов.
Электромагнитные поля и волны. Лекция 12.
1

2. 1 Электромагнитные колебания в объемных резонаторах

Рисунок 3.1 – Схема колебательного контура
в низкочастотной цепи
Принцип работы: переход энергии электрического поля
конденсатора в магнитное поле катушки и наоборот.
Основное свойство - частотная избирательность по отношению к
внешнему гармоническому воздействию: амплитуда его
колебаний максимальна на резонансной частоте и уменьшается
по мере удаления от нее.
Основное назначение –поддержание в течение длительного
времени периодических колебаний, вызванных внешним
импульсом.
Применение резонаторов - неотъемлемая часть многих
усилителей, большинства генераторов, приемников, частотных
фильтров и измерителей частоты.
2
Электромагнитные поля и волны. Лекция 12.

3.

Аналог колебательного контура в
высокочастотной области – резонатор.
Рисунок 3.2 – Геометрия закрытого
резонатора
Принцип работы: использование
колебательного процесса перехода
электрического поля в магнитное в электромагнитной волне. (В
теореме Умова-Пойнтинга данный процесс описывается
слагаемым
B
D
H t E t dv
V
Для исключения потерь на излучение объем, в котором
сосредоточено поле, изолируется металлом. Конструкция
называется объемным резонатором.
Электромагнитные поля и волны. Лекция 12.
3

4.

а
б
Рисунок 3.3 – Примеры конструкции резонаторов:
а – в виде короткозамкнутого отрезка волновода;
б - отрезок диэлектрического стержня.
Электромагнитные поля и волны. Лекция 12.
4

5.

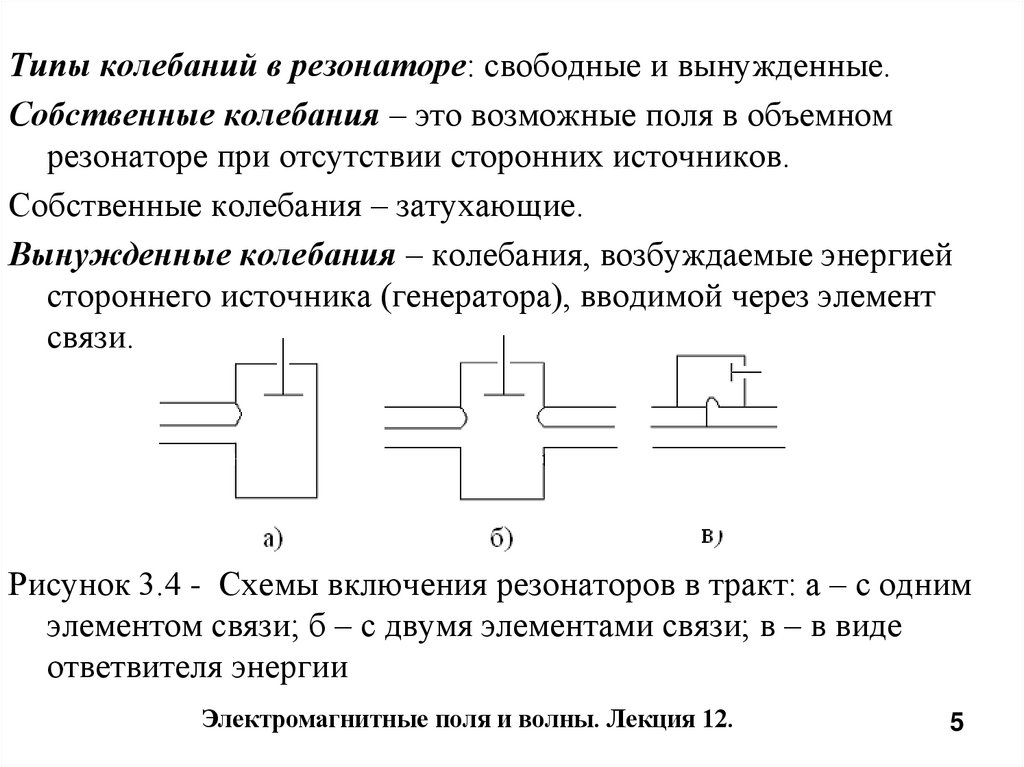
Типы колебаний в резонаторе: свободные и вынужденные.
Собственные колебания – это возможные поля в объемном
резонаторе при отсутствии сторонних источников.
Собственные колебания – затухающие.
Вынужденные колебания – колебания, возбуждаемые энергией
стороннего источника (генератора), вводимой через элемент
связи.
Рисунок 3.4 - Схемы включения резонаторов в тракт: а – с одним
элементом связи; б – с двумя элементами связи; в – в виде
ответвителя энергии
Электромагнитные поля и волны. Лекция 12.
5

6. 2 Поля в полых прямоугольных и круглых резонаторах

Структура поля в резонаторе
Наиболее простым вариантов выполнения полого закрытого
резонатора является введение металлических стенок
(закороток) в волновод.
Введение стенок выполняется так, чтобы внутри отрезка
волновода укладывалось целое число полуволн.
Получающаяся стоячая волна - результат многократных
упорядоченных отражений исходной бегущей волны
регулярного волновода от обеих поперечных стенок.
Электромагнитные поля и волны. Лекция 12.
6

7.

Комплексные амплитуды полей:
m n y l z
Ex Ex 0 cos
x sin
sin
a b d
m n y l z
E y E y 0 sin
x cos
sin
a b d
m n y l z
E z E z 0 sin
x sin
sin
a b d
z E y y Ez
m n y l z
H x i
sin
x cos
cos
a b d
x Ez z Ex
m n y l z
H y i
cos
x sin
cos
a b d
y Ex x E y
m n y l z
H z i
cos
x cos
sin
a b d
Электромагнитные поля и волны. Лекция 12.
(3.1)
(3.2)
(3.3)
(3.4)
(3.5)
(3.6)
7

8.

Длины волн собственных колебаний: s
2
2
1
2
d кр
(3.7)
Тип колебаний в резонаторе, имеющий наибольшую длину волны
собственных колебаний, называют основным.
Типы колебаний, имеющие различные структуры, но одинаковые
собственные длины волн, называют вырожденными.
Вырождение рабочего типа колебаний приводит к усложнению
структуры поля в резонаторе, увеличению потерь в нем и
искажению его частотных характеристик.
Подавление вырожденного паразитного типа осуществляется
обеспечением его сильного затухания в резонаторе.
Электромагнитные поля и волны. Лекция 12.
8

9.

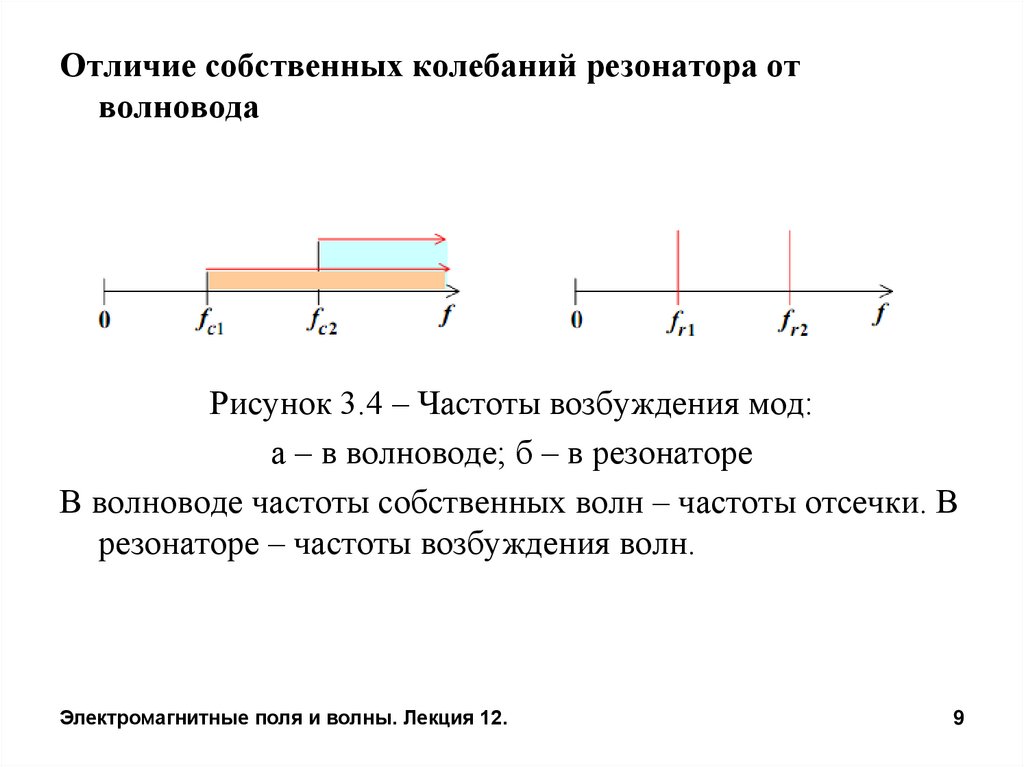
Отличие собственных колебаний резонатора от
волновода
Рисунок 3.4 – Частоты возбуждения мод:
а – в волноводе; б – в резонаторе
В волноводе частоты собственных волн – частоты отсечки. В
резонаторе – частоты возбуждения волн.
Электромагнитные поля и волны. Лекция 12.
9

10.

В прямоугольном резонаторе все три координатных оси
равноправны. Разделение на типы колебаний чисто условное.
Длина волны собственных колебаний:
2
mnl
2
2
2
(3.8)
m
n
a b d
Наибольшее значение критической длины волны (при основном
типе колебаний) получается, если индекс при наименьшем ребре
резонатора равен нулю и оба остальных индекса равны единице.
Типы колебаний с тремя отличными от нуля индексами, по
крайней мере, двукратно вырождены.
Наибольшая собственная длина волны сравнима с линейными
размерами резонатора.
Наиболее часть используемым типом колебаний в прямоугольном
резонаторе является колебание Н101.
Электромагнитные поля и волны. Лекция 12.
10

11.

В круглых резонаторах длина
колебаний определяется формулой:
волны
собственных
2
mnl
mn
a d
2
2
где mn mn - для волны типа Н и
,
(3.9)
mn 'mn - типа Е.
Другой вид формулы (3.9):
D
mnl
2
D mn
,
4 d
2
2
2
(3.10)
где D 2a - диаметр резонатора.
Основными типами колебаний в кругом волноводе являются
Н011 и Е010.
Электромагнитные поля и волны. Лекция 12.
11

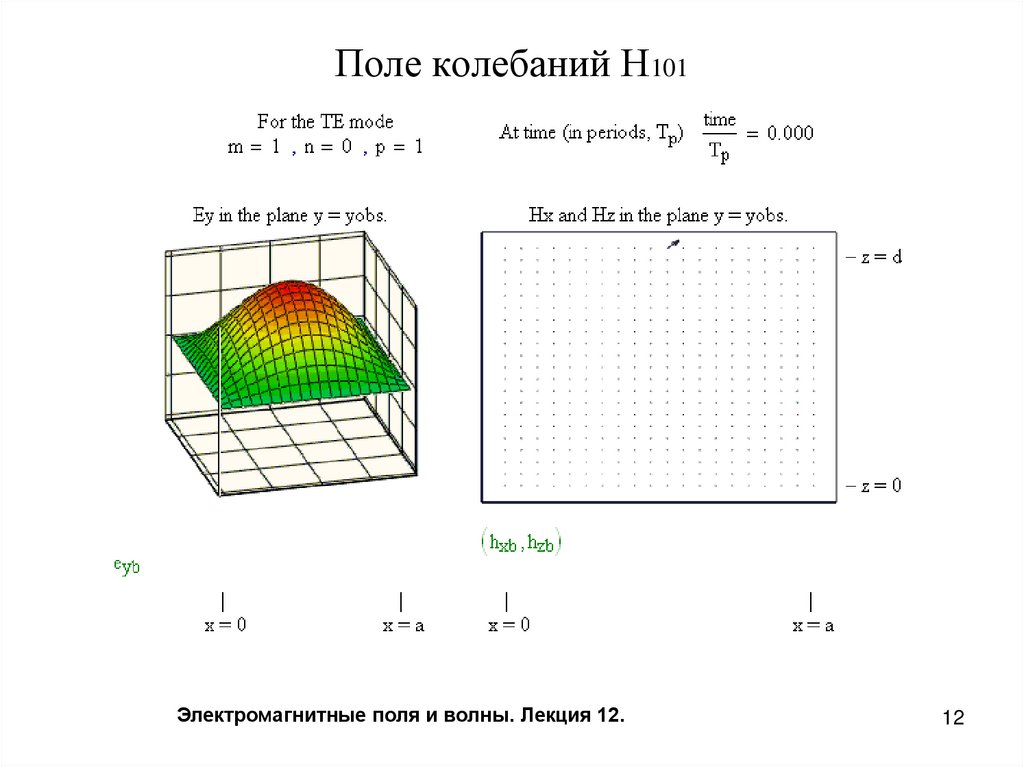
12. Поле колебаний Н101

Электромагнитные поля и волны. Лекция 12.
12

13.

3 Добротность объемных резонаторов
Добротностью объемного резонатора для s-го типа, определяющей
полосу пропускания системы и скорость затухания собственных
колебаний, называют отношение
w
w
Qs 2
s
(3.11)
wп
Pп.ср.
где w – запасенная при резонансе внутри полости электромагнитная
энергия s-го типа колебаний;
wп Pп.срTs – энергия полных потерь за время одного
периода Ts ;
Pп.ср - средняя за период мощность полных потерь;
s - частота собственных колебаний.
Связь между добротностью и длительностью колебаний:
W Wнач exp(
Q
t)
Электромагнитные поля и волны. Лекция 12.
(3.12)
13

14.

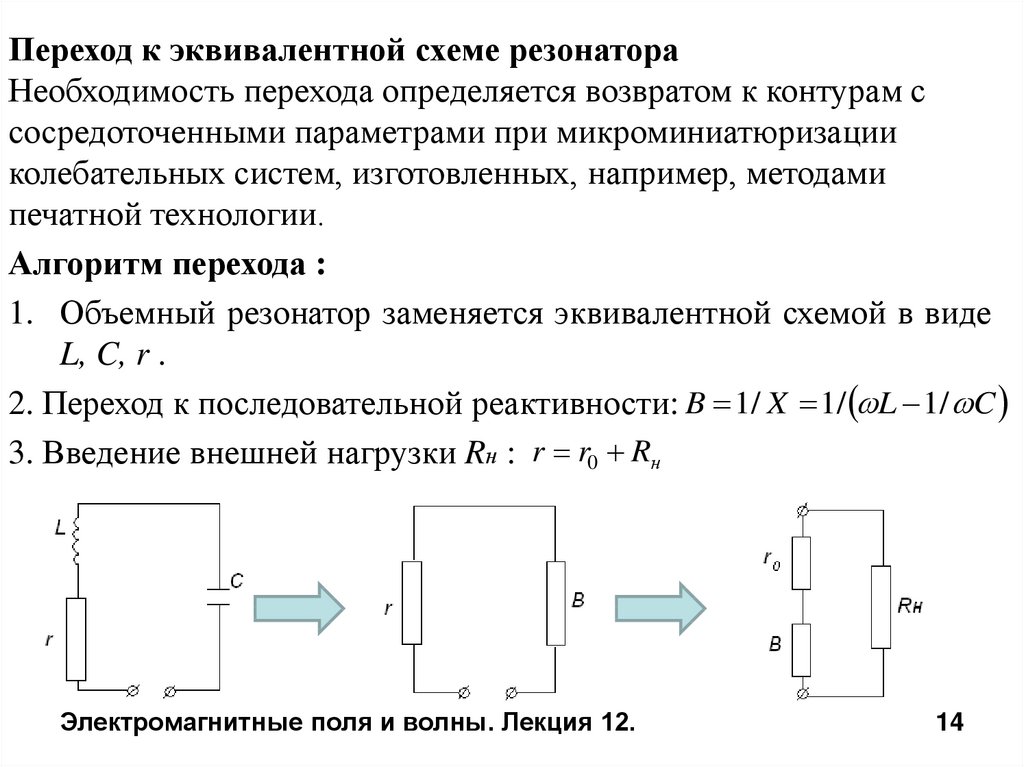
Переход к эквивалентной схеме резонатора
Необходимость перехода определяется возвратом к контурам с
сосредоточенными параметрами при микроминиатюризации
колебательных систем, изготовленных, например, методами
печатной технологии.
Алгоритм перехода :
1. Объемный резонатор заменяется эквивалентной схемой в виде
L, C, r .
2. Переход к последовательной реактивности: B 1/ X 1/ L 1/ C
3. Введение внешней нагрузки Rн : r r0 Rн
Электромагнитные поля и волны. Лекция 12.
14

15.

Нагруженная добротность Qн включает:
- собственную (ненагруженную) Q0 ;
- внешнюю Qвн.
Собственная (ненагруженная) добротность Q0 учитывает энергию,
рассеянную в самом резонаторе на резонансной частоте.
Добротность, зависящую от мощности полных потерь, часто
называют нагруженной добротностью резонатора Qн.
(3.13)
1 / Qн 1 / Q0 1 / Qвн
С учетом эквивалентной схемы величина собственной добротности:
CЭ
(3.14)
Q
R L/r
0
LЭ
Э
0
0
Величина собственной добротности не зависит от применяемой
эквивалентной схемы, т.к. не зависит от вида связи.
Внешняя нагрузка:
Qвн 0 L / rвн
(3.15)
Электромагнитные поля и волны. Лекция 12.
15

16.

Определение частичных добротностей
Энергия, запасенная в резонаторе, может быть найдена через
максимальную энергию одного из этих полей:
a1
a1
(3.16)
2 V
2 V
Частичная добротность при заполнении материалом с потерями:
a1
w
w
1
Qsд s
s
s
э
1
(3.15)
Pд.ср
2
tg
1
1
E
dV
m
2 V
Частичная добротность, обусловленная потерями в стенках:
2
H
m dV
a1 V
w
(3.16)
Qs.м s
s
Pм.ср
rs H 2 m dS
w wэ.макс
Em2 dV
wм.макс
2
H
m dV
a 2 s
rs
- активное поверхностное сопротивление стенок;
2 2
H m
- амплитуда касательной к стенке компоненты вектора .
S
Электромагнитные поля и волны. Лекция 12.
16

17.

Собственные добротности для различных типов колебаний
Прямоугольный резонатор:
mnp a
abd(a 2 b2 )
(3.17)
Q
H101
a3 (d 2b) d 3 (a 2b)
rS
Круглый резонатор:
QE010
QE011
QH 011
mnp a ad
2rS
mnp a
2rS
a d
(3.18)
ad
2a d
(3.19)
2
mnp a mnp
a a a 2d
2
2rS 02 d
2 a
2
a
Электромагнитные поля и волны. Лекция 12.
(3.20)
d
17