Similar presentations:
Пирамида. Сечения пирамиды
1. Добрый день! Начинаем урок!
2.
Отгадав загадку, Вы узнаете тему урока.Загадка.
Кто в Египте побывал
Сразу же ее узнал
Основание, вершины,
Грани три или четыре
Что же это? Назовите.
И на слайде покажите.
3.
ПИРАМИДА4. Тема урока:
«Пирамида.Сечения
пирамиды»
5. Какие у вас возникают ассоциации, когда вы слышите слово «пирамида»?
Пирамида (геометрия) — тип многогранников.Пирамида (архитектура) — вид архитектурного сооружения в
форме пирамиды.
Пирамида (бильярд) — разновидность бильярда.
Финансовая пирамида — сомнительная схема привлечения
инвестиций, описываемая моделью пирамиды.
Пирамида знаний — это условная фигура, в рамках которой
человека можно классифицировать по уровню и охвату знаний,
которые схематично отображаются в виде уровней этой
фигуры.
6. Пирамида (павильон) — один из первых павильонов пейзажной части Екатерининского парка в Царском Селе.
ПирамидаВ 1770–1772 годах по проекту архитектора
В. И. Неелова был возведен один из первых
павильонов
пейзажной
части
Екатерининского парка — Пирамида, уже в
1774 году разобранная и в 1782–1783 годах
отстроенная
заново
Ч.
Камероном.
Позеленевшая, заросшая мхом поверхность
этого традиционного для парков конца XVIII
столетия романтической эпохи сооружения
придает ему черты древнего мавзолея.
Пирамида сознательно была расположена в
стороне от главной дорожки, чтобы
гуляющий,
умиротворенный
тишиной
тенистого парка, мог случайно набрести на
нее
и
отдаться
нахлынувшим
воспоминаниям.
Внутреннее
помещение
павильона
перекрыто
сферическим
куполом
с
отверстием в центре; в стенах устроены
ниши для хранения урн.
С противоположной от входа стороны, у
подножия Пирамиды, похоронены три
любимые собачки Екатерины II: Том
Андерсон, Земира и Дюшес.
7. Пирамида — элемент художественной, силовой и пластической акробатики (либо в парашютном спорте), групповое расположение
акробатов, которые, поддерживая друг друга,образуют сложные фигуры.
8. Пирамида здорового питания — схематическое представление принципа здорового питания
9. Пищевые отношения в Природе. Отображение цепи питания - “экологическая пирамида”
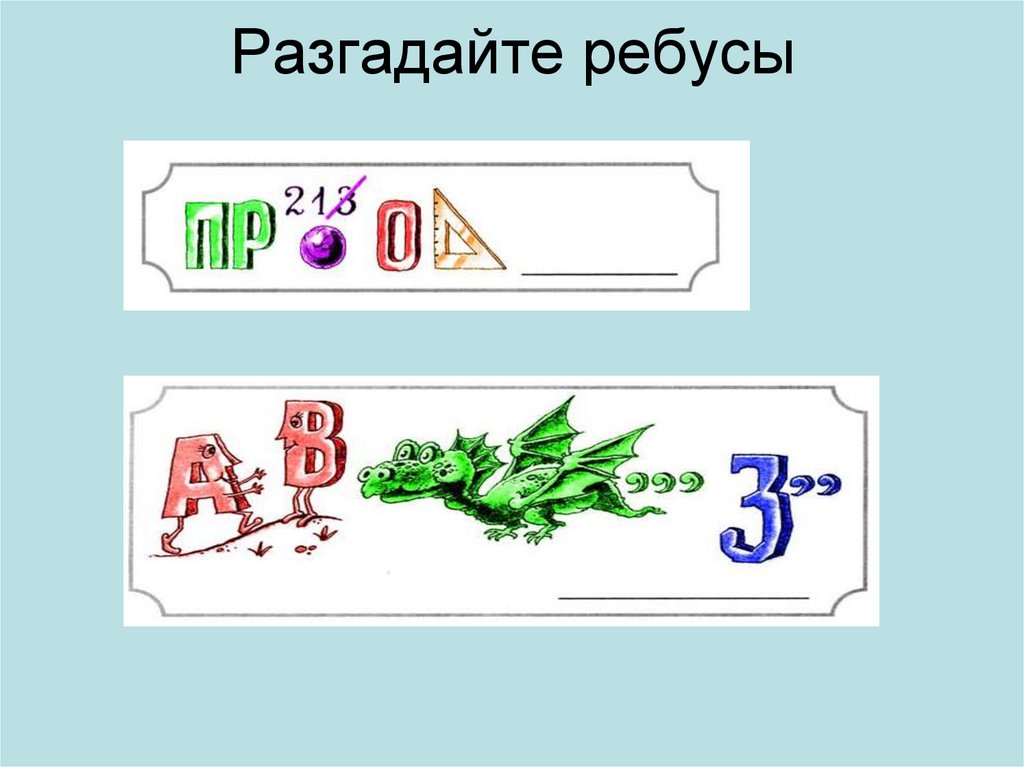
10. Разгадайте ребусы
11.
12. Запишите в тетрадь
Пирамидой называется многогранник, которыйсостоит из плоского многоугольника – основания
пирамиды, точки, не лежащей в плоскости
основания, - вершины пирамиды и всех отрезков,
соединяющих вершину пирамиды с точками
основания.
Отрезки, соединяющие вершину пирамиды с
вершинами основания, называются боковыми
ребрами.
Поверхность пирамиды состоит из основания и
боковых граней.
Каждая боковая грань – треугольник. Одной из его
вершин является вершина пирамиды, а
противолежащей стороной – сторона основания
пирамиды.
Высотой пирамиды называется перпендикуляр,
опущенный из вершины пирамиды на плоскость
основания.
Основание – многоугольник A1A2…An.
Вершина пирамиды – P.
Боковые ребра – PA1, PA2, …, PAn.
Боковые грани – ΔPA1A2, ΔPA2A3, ….
Высота пирамиды – PH.
13.
вершиныребро
основания
боковое
ребро
боковая
грань
основание
14.
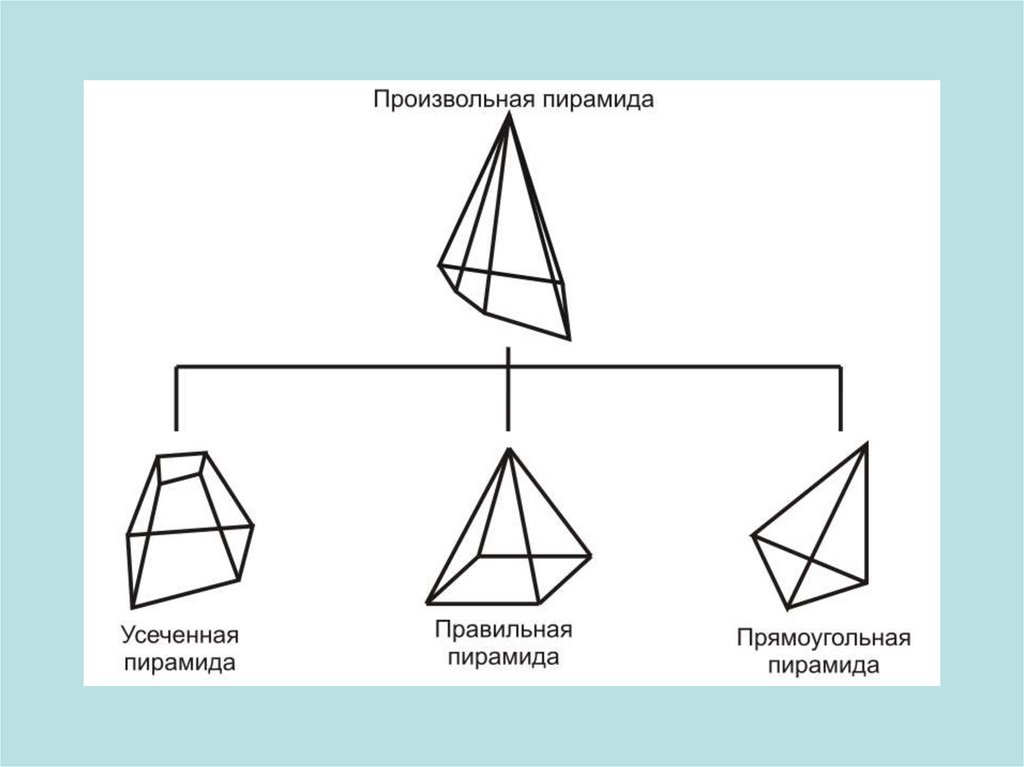
Пирамида называется n-угольной, если ее основанием являетсяn-угольник.
Пирамида называется правильной, если ее основание –
правильный многоугольник, а высота проходит через центр
основания. Ее высота – отрезок, соединяющий вершину
пирамиды с ее центром.
Апофемой боковой грани правильной пирамиды называется
высота этой грани, проведенная из вершины пирамиды.
Плоскость, пересекающая пирамиду и параллельная ее
основанию, отсекает ее на подобную пирамиду и усеченную
пирамиду.
Пирамида называется прямоугольной, если одно из боковых
рёбер пирамиды перпендикулярно основанию. В данном
случае, это ребро и является высотой пирамиды.
15.
16.
17. Формулы, связанные с пирамидой
1Объём пирамиды может быть вычислен по формуле: V Sh
3
где S — площадь основания и h — высота;
Боковая поверхность — это сумма площадей боковых граней:
Sb Si
Полная поверхность — это сумма боковой поверхности и
площади основания: Sp = Sb + So
Для нахождения боковой поверхности в правильной
i
пирамиде можно использовать формулы:
1
n 2
Sb Pa b sin
2
2
где a — апофема боковой грани, P — периметр основания,
n — число сторон основания, b — боковое ребро, α —
плоский угол при вершине пирамиды.
18.
ТестЗадача 1.
Чему равна площадь боковой поверхности
правильной
четырёхугольной пирамиды со
стороной в основании 4,5см и апофемой 5см?
А. 90см2
Задача 2.
В. 101,25см2
Вычислите объём правильной
треугольной
пирамиды со стороной в основании 6 дм и высотой
пирамиды 8дм.
А. 24 3 дм3
Задача 3.
Б. 45см2
Б. 72 3 дм3
В.144 3 дм3
Какой объём имеет деревянная шпала длиной 2,7м, толщиной 0,18м и
шириной 0,25м.
А. 3,13 м3
Б. 0,1215 м3
В. 0,531 м3
19.
Что означает этот Ребус?‛‛
РАЗ ОТВЁРТКА
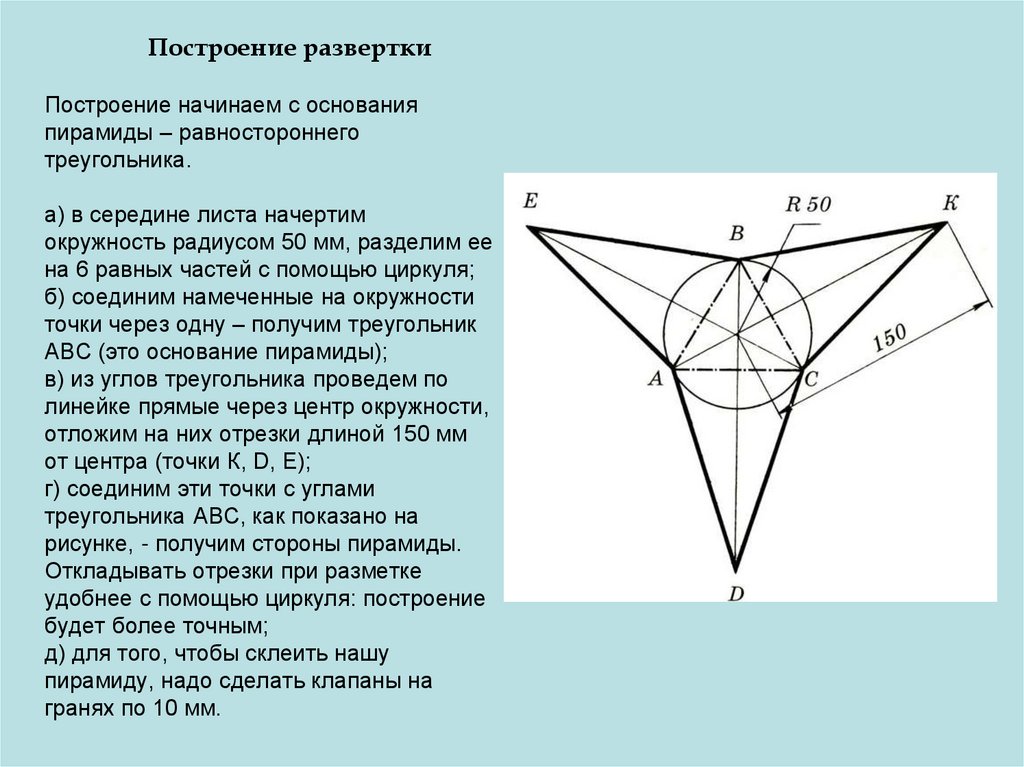
20. Построение развертки Построение начинаем с основания пирамиды – равностороннего треугольника. а) в середине листа начертим
окружность радиусом 50 мм, разделим еена 6 равных частей с помощью циркуля;
б) соединим намеченные на окружности
точки через одну – получим треугольник
ABC (это основание пирамиды);
в) из углов треугольника проведем по
линейке прямые через центр окружности,
отложим на них отрезки длиной 150 мм
от центра (точки К, D, Е);
г) соединим эти точки с углами
треугольника ABC, как показано на
рисунке, - получим стороны пирамиды.
Откладывать отрезки при разметке
удобнее с помощью циркуля: построение
будет более точным;
д) для того, чтобы склеить нашу
пирамиду, надо сделать клапаны на
гранях по 10 мм.
21.
Пирамида, у которой 4грани - четырехгранная.
22.
Трехгранная пирамида,у которой 3 грани.
23.
Пятигранная пирамида24. ПОСТРОЕНИЕ ПИРАМИДЫ И ЕЕ ПЛОСКИХ СЕЧЕНИИ
В соответствии с правилами параллельного проектированияизображение пирамиды строится следующим образом. Сначала
строится основание. Это будет некоторый плоский
многоугольник. Затем отмечается вершина пирамиды, которая
соединяется боковыми ребрами с вершинами основания.
Сечения пирамиды плоскостями, проходящими через ее
вершину, представляют собой треугольники.
25.
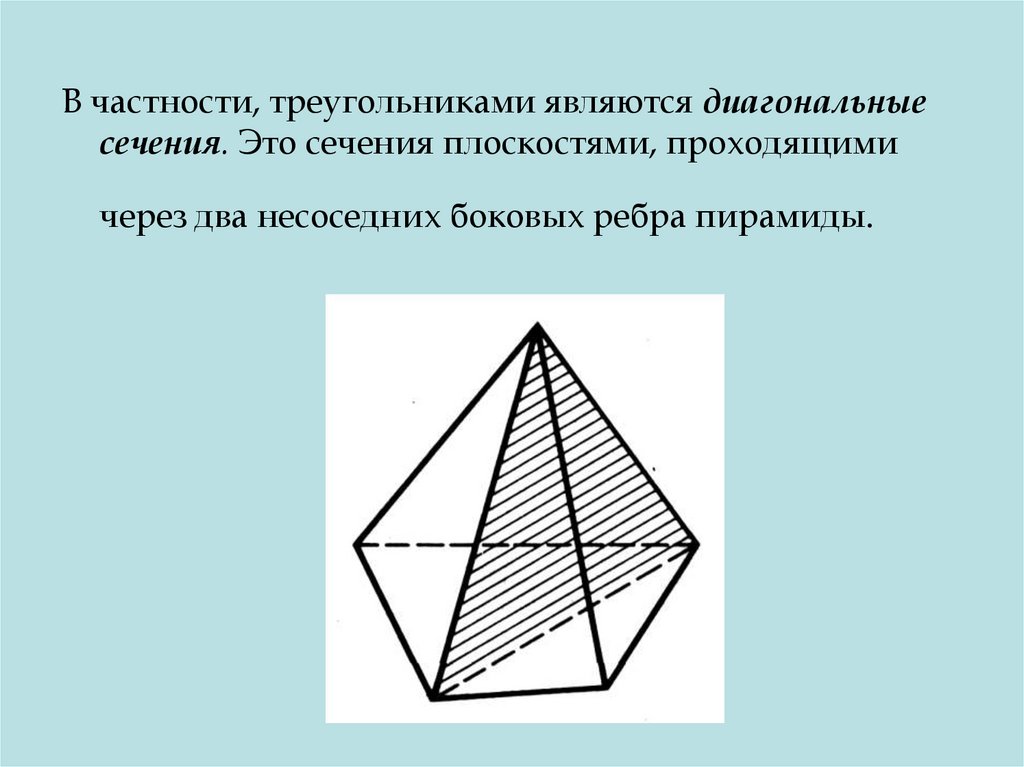
В частности, треугольниками являются диагональныесечения. Это сечения плоскостями, проходящими
через два несоседних боковых ребра пирамиды.
26. Для построения сечения пирамиды плоскостью с заданным следом g на плоскости основания достаточно построить пересечения ее
боковых граней с секущей плоскостью.Если на грани, не параллельной следу g, известна какаянибудь точка А, принадлежащая сечению, то сначала строится
пересечение следа g секущей плоскости с плоскостью этой
грани — точка D на рисунке.
Точка D соединяется с точкой А прямой. Тогда отрезок
этой прямой, принадлежащий грани, есть пересечение этой
грани с секущей плоскостью.
27. Если точка А лежит на грани, параллельной следу g, то секущая плоскость пересекает эту грань по отрезку, параллельному прямой
g. Переходя к соседней боковой грани, строят ее пересечение ссекущей плоскостью и так далее. В итоге получается требуемое
сечение пирамиды.
На рисунке построено сечение четырехугольной пирамиды
плоскостью, проходящей через сторону основания и точку А на
одном из ее боковых ребер.
28. Задача. Дан тетраэдр ABCD. Построить сечение тетраэдра плоскостью, параллельной грани ACD и проходящей через точку M ребра DB.
РN
М
Построение:
1. строим MP, MP || DA;
2. MN, MN || CD;
3. Соединяем PN;
4. ∆MNP – искомое сечение.
























 mathematics
mathematics








