Пирамида. Определение пирамиды и её элементов

1. Пирамида

2. Основные вопросы:

• Определение пирамиды и её элементов:
основания, вершины, боковых ребер и
граней, высоты.
• Определение n – угольной пирамиды:
тетраэдра.
• Правильная пирамида.
• Площадь поверхности пирамиды.
• Усеченная пирамида и её элементы.
Свойства параллельных сечений в
пирамиде.
2

3.

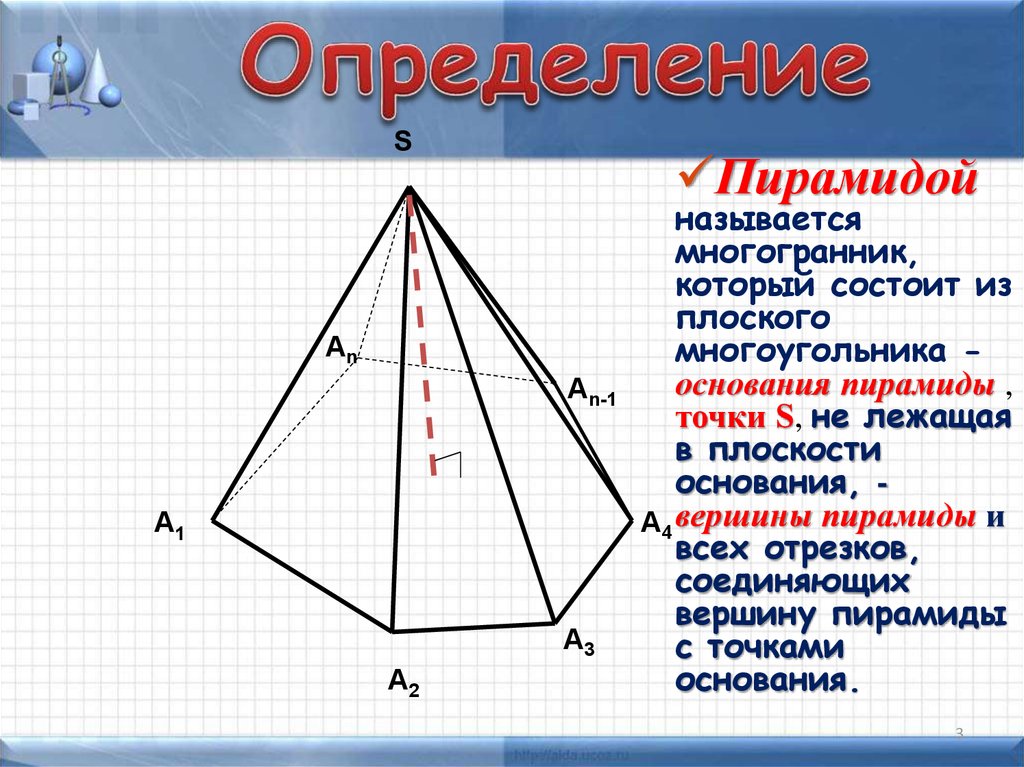
S
Пирамидой
Аn
Аn-1
А1
А3
А2
называется
многогранник,
который состоит из
плоского
многоугольника основания пирамиды ,
точки S, не лежащая
в плоскости
основания, А4 вершины пирамиды и
всех отрезков,
соединяющих
вершину пирамиды
с точками
основания.
3

4.

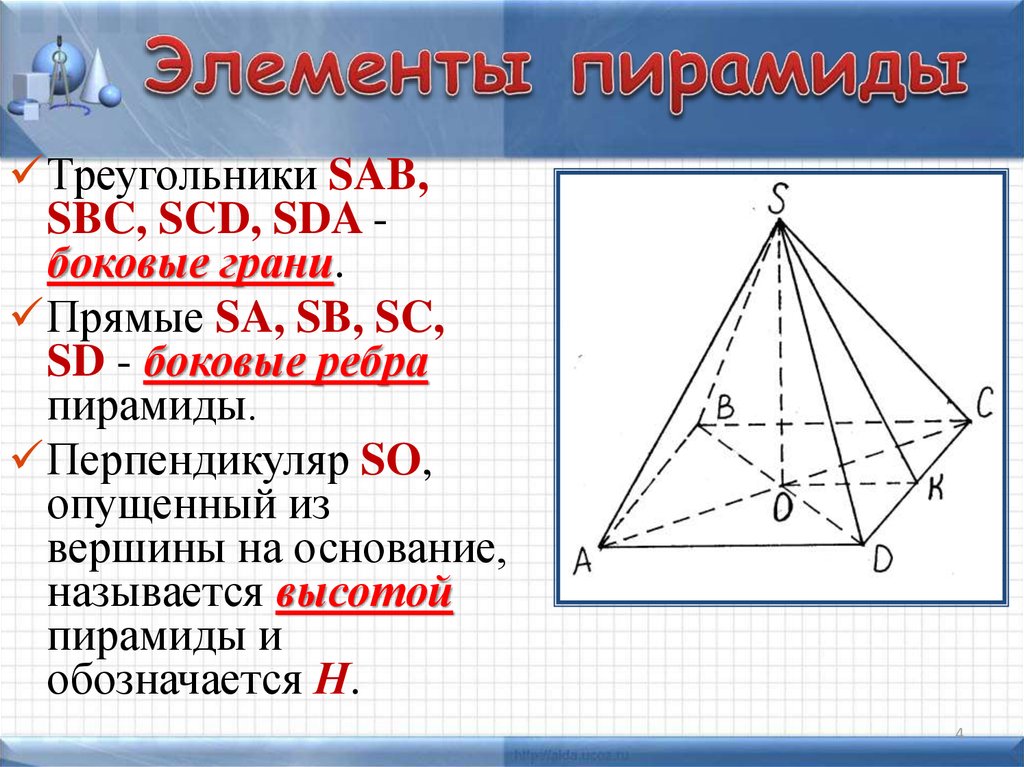
Треугольники SAB,
SBC, SCD, SDA боковые грани.
Прямые SA, SB, SC,
SD - боковые ребра
пирамиды.
Перпендикуляр SO,
опущенный из
вершины на основание,
называется высотой
пирамиды и
обозначается Н.
4

5. Высота проецируется

В вершину
основания
На сторону
основания
Во внутреннюю
область
основания
Во внешнюю
область
основания
5

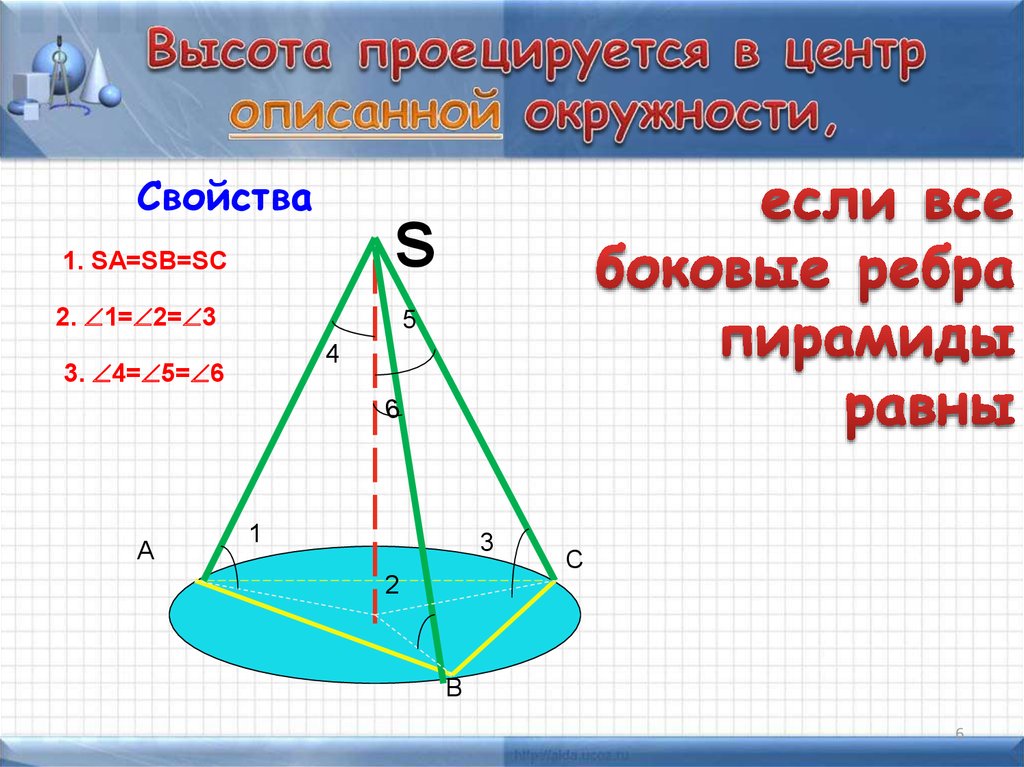
6. Высота проецируется в центр описанной окружности,

Свойства
s
1. SA=SB=SC
2. 1= 2= 3
5
4
3. 4= 5= 6
A
1
3
C
2
B
6

7. Высота проецируется в центр вписанной окружности,

Свойства
S
1.SM=SN=SK
2. 1= 2= 3
5
3. 4= 5= 6
K
1
4
3
2
N
M
7

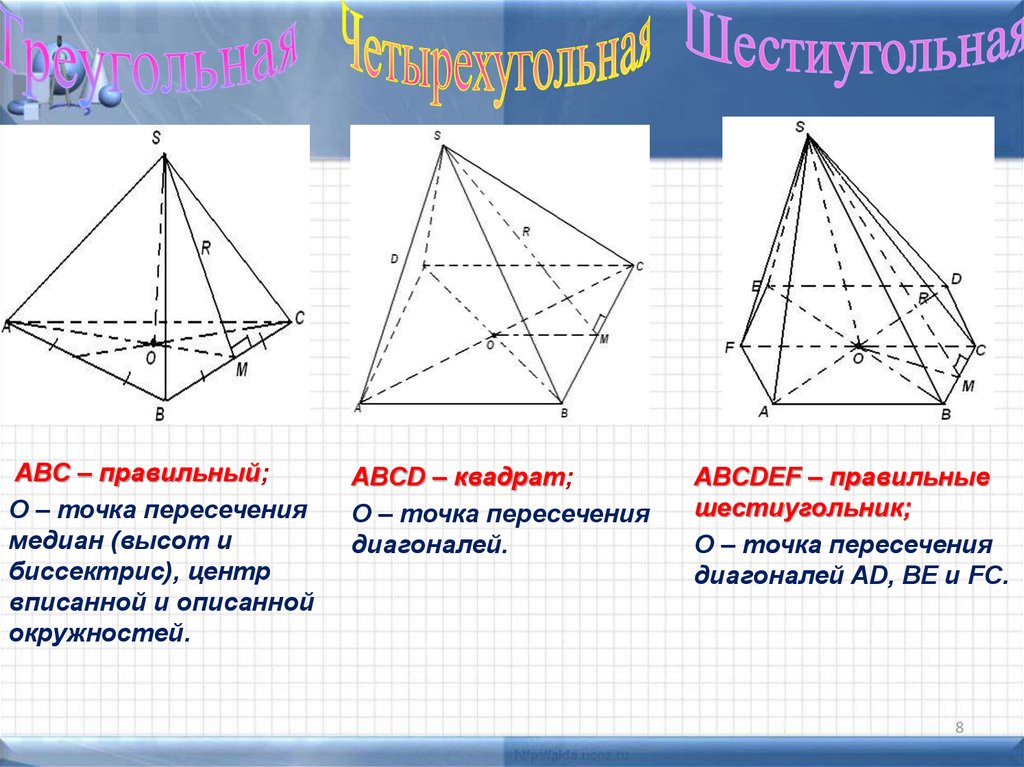
8.

ABC – правильный;
О – точка пересечения
медиан (высот и
биссектрис), центр
вписанной и описанной
окружностей.
ABCD – квадрат;
О – точка пересечения
диагоналей.
ABCDEF – правильные
шестиугольник;
О – точка пересечения
диагоналей AD, BE и FC.
8

9. Тетраэдр -

S
B
A
H
SABC - тетраэдр
C
треугольная
пирамида,
все четыре грани
которой –
треугольники, и
любая из них
может быть
принята за
основание.
9

10. Свойства тетраэдра

10

11. Правильная пирамида

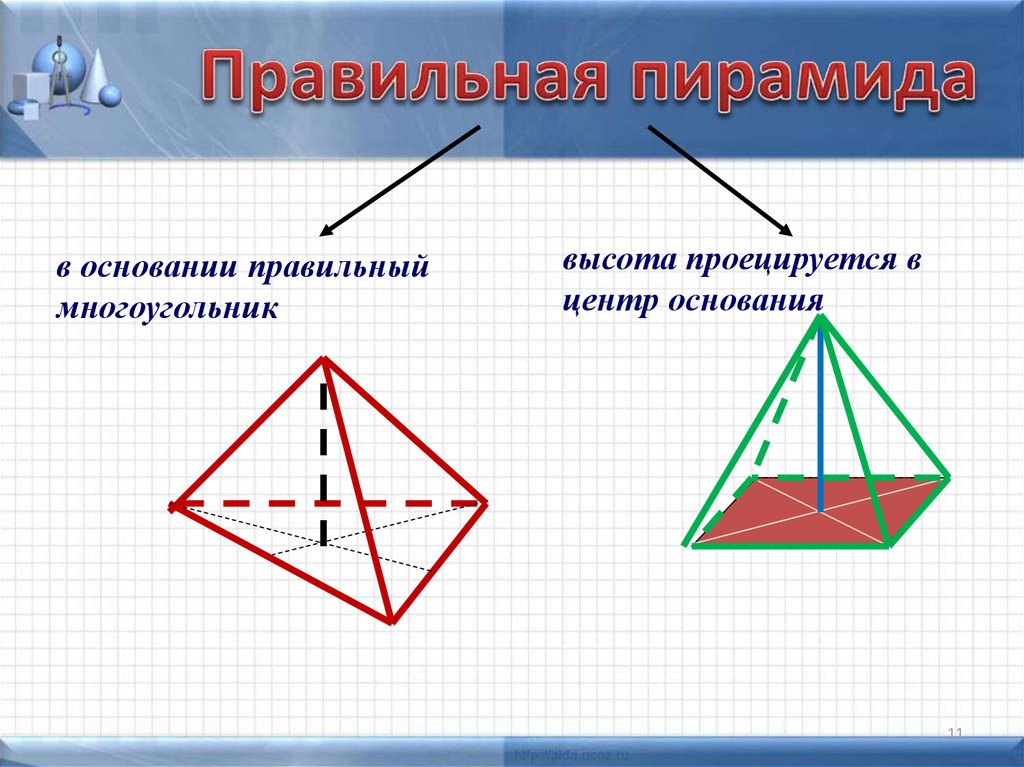
в основании правильный
многоугольник
высота проецируется в
центр основания
11

12. Правильная пирамида

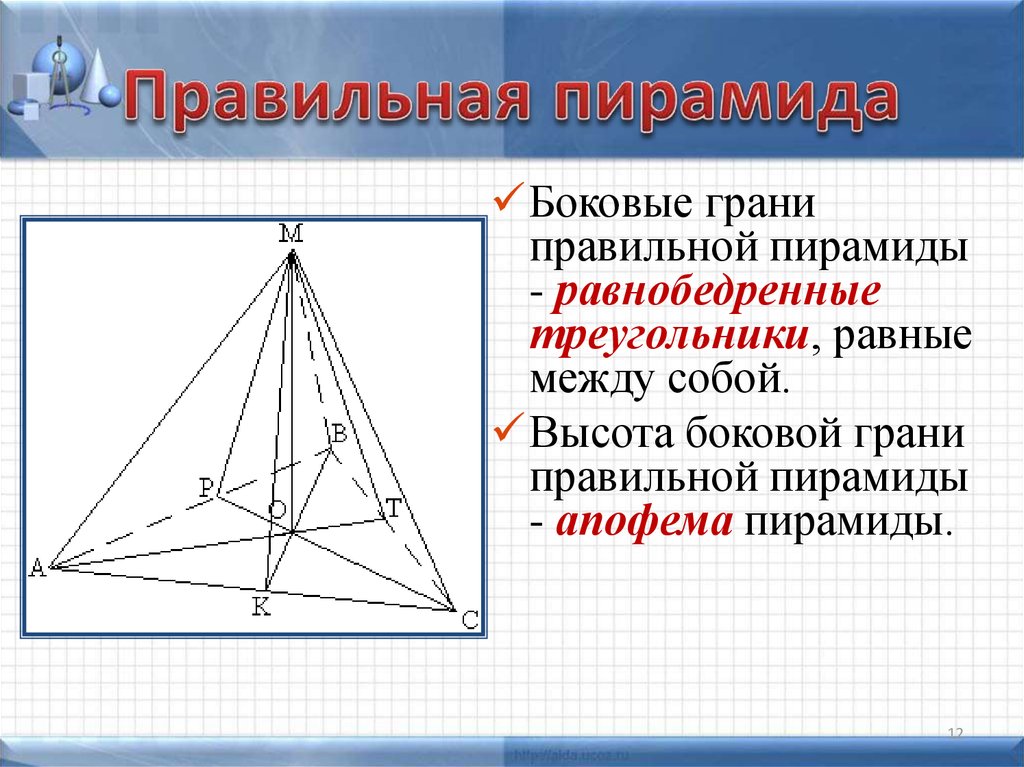
Боковые грани
правильной пирамиды
- равнобедренные
треугольники, равные
между собой.
Высота боковой грани
правильной пирамиды
- апофема пирамиды.
12

13. Свойства правильной пирамиды

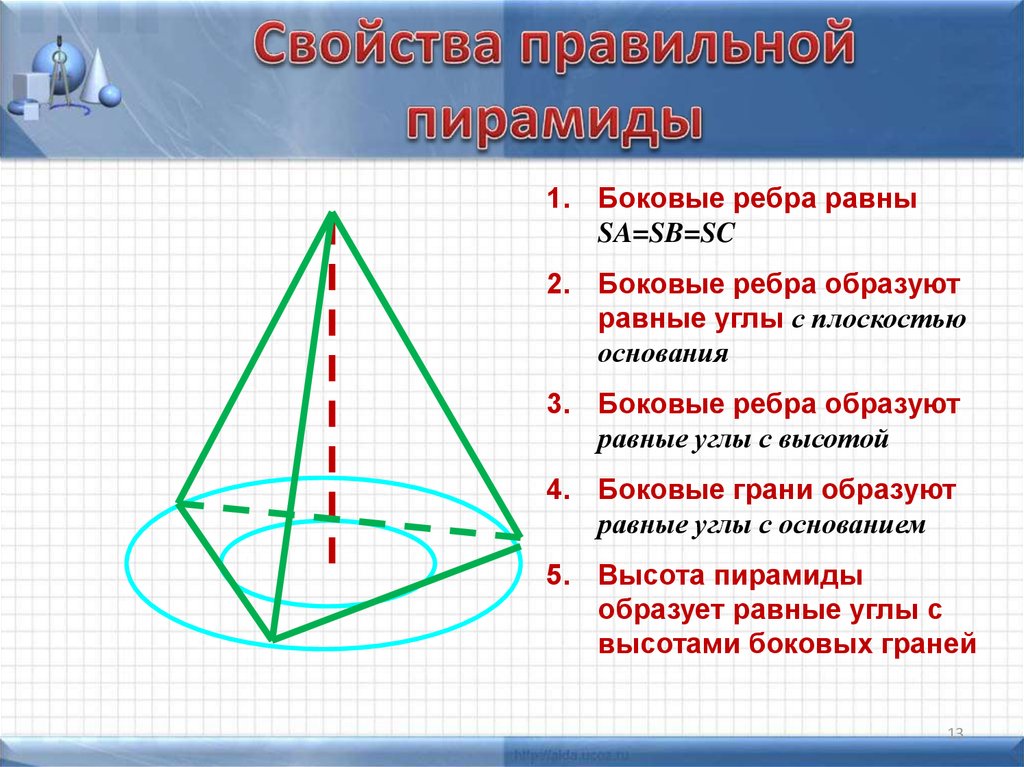
1. Боковые ребра равны
SA=SB=SC
2. Боковые ребра образуют
равные углы с плоскостью
основания
3. Боковые ребра образуют
равные углы с высотой
4. Боковые грани образуют
равные углы с основанием
5. Высота пирамиды
образует равные углы с
высотами боковых граней
13

14.

Площадь боковой
поверхности
правильной пирамиды
равна половине
произведения
периметра основания
на апофему.

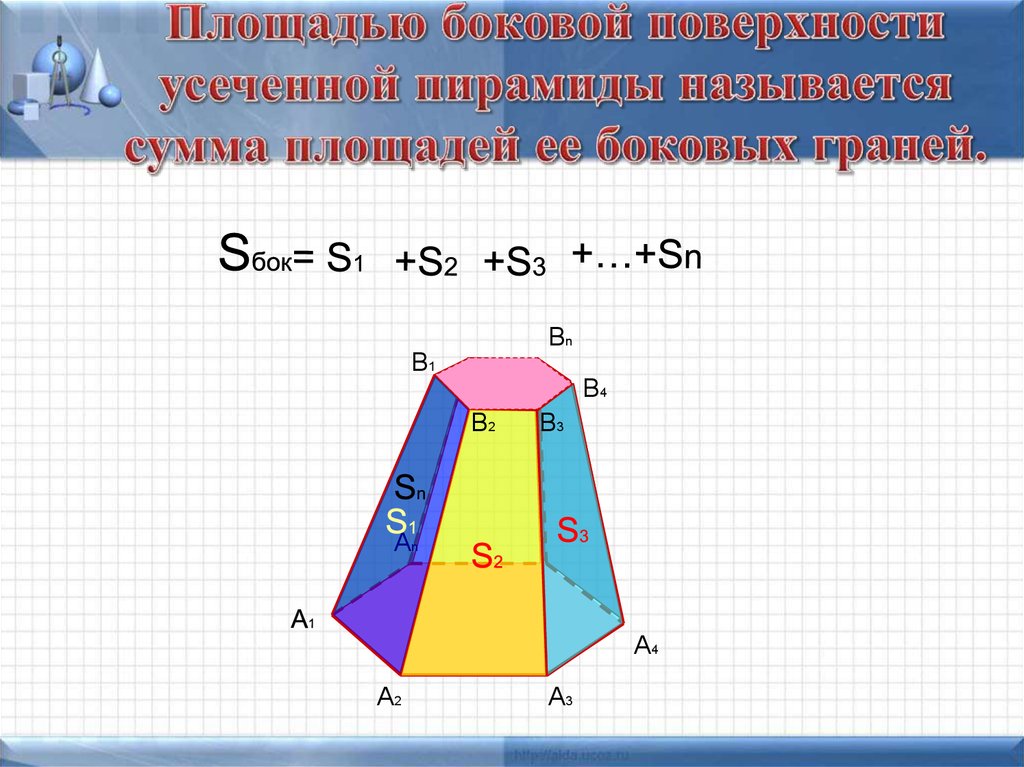
15. Площадь пирамиды

Площадью полной
поверхности
пирамиды называется сумма
площадей
всех его граней
Площадь боковой
поверхности пирамиды равна
сумма
площадей ее боковых граней
15

16.

боковые ребра и высота делятся
этой плоскостью на
пропорциональные отрезки в
отношении :
площади сечения и основания
пирамиды относятся как
квадраты их расстояний до
вершины пирамиды:
16

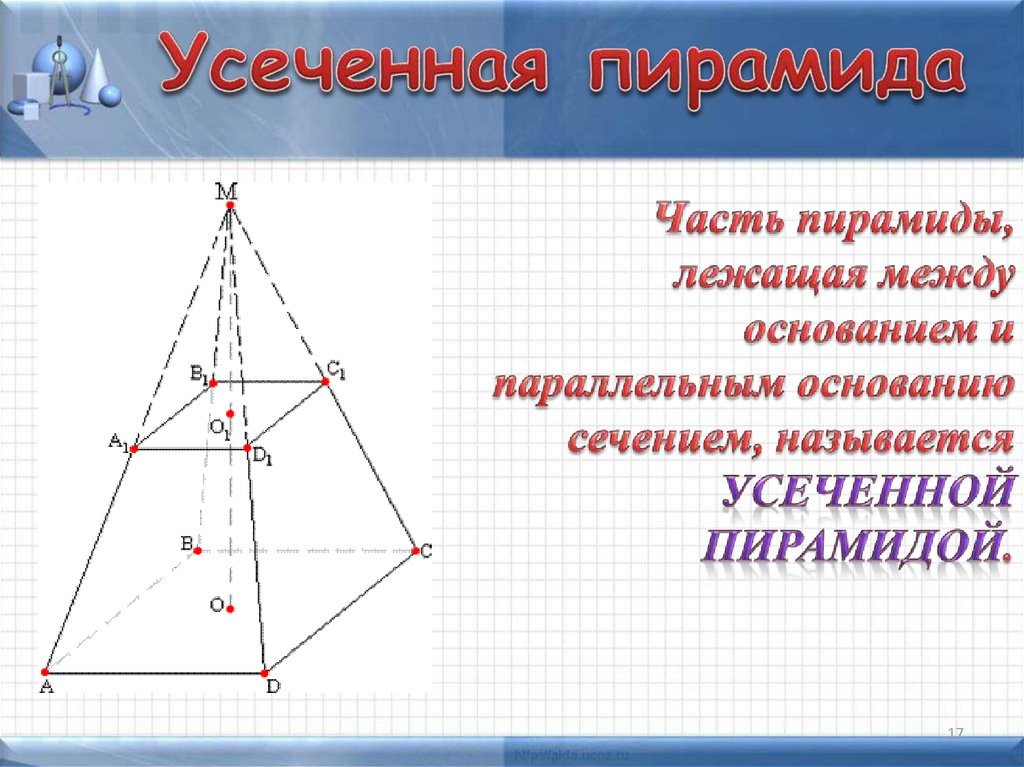
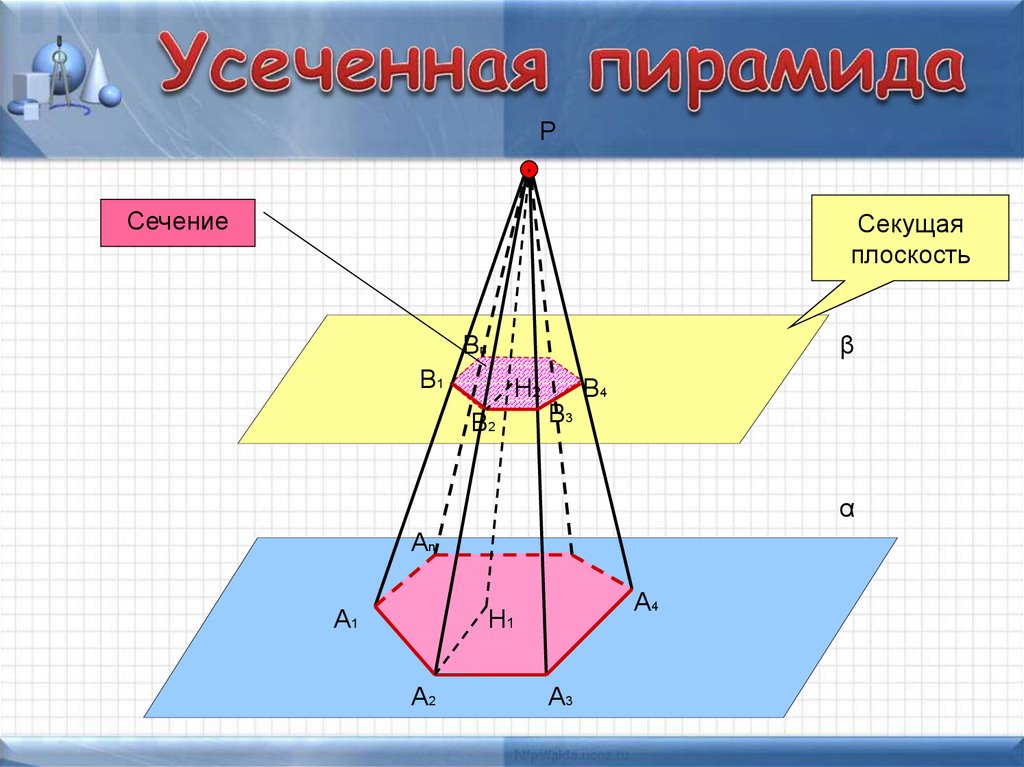
17. Усеченная пирамида

17

18. Усеченная пирамида

P
Сечение
Секущая
плоскость
Вn
β
В1
Н2
В2
В3
В4
α
An
A4
Н1
A1
A2
A3

19. Усеченная пирамида

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости
другого основания, называется ВЫСОТОЙ усеченной пирамиды
Вn
В1
В4
В2
В3
An
A4
A2
A3

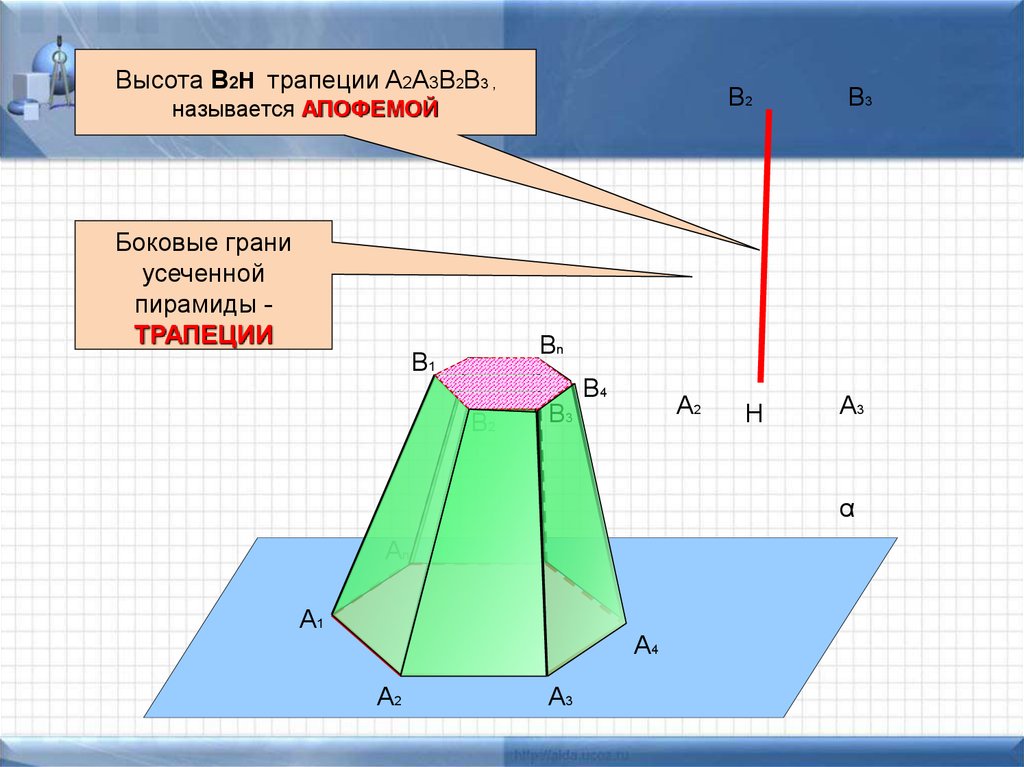
20.

Высота B2H трапеции A2A3B2B3 ,
В2
называется АПОФЕМОЙ
Боковые грани
усеченной
пирамиды ТРАПЕЦИИ
В3
Вn
В1
В2
В3
В4
A2
H
A3
α
An
A1
A4
A2
A3

21.

Усеченная пирамида называется правильной, если она
получена сечением правильной пирамиды
плоскостью, параллельной основанию.
Основания правильной усеченной пирамиды — правильные
многоугольники, а боковые грани — равнобедренные
P
трапеции.
Равнобедренная трапеция
Правильный многоугольник
В1
β
Вn
В4
В2
В3
An
α
A1
A4
A2
A3

22.

Вn
В1
В4
В2
В3
An
A4
A2
A3

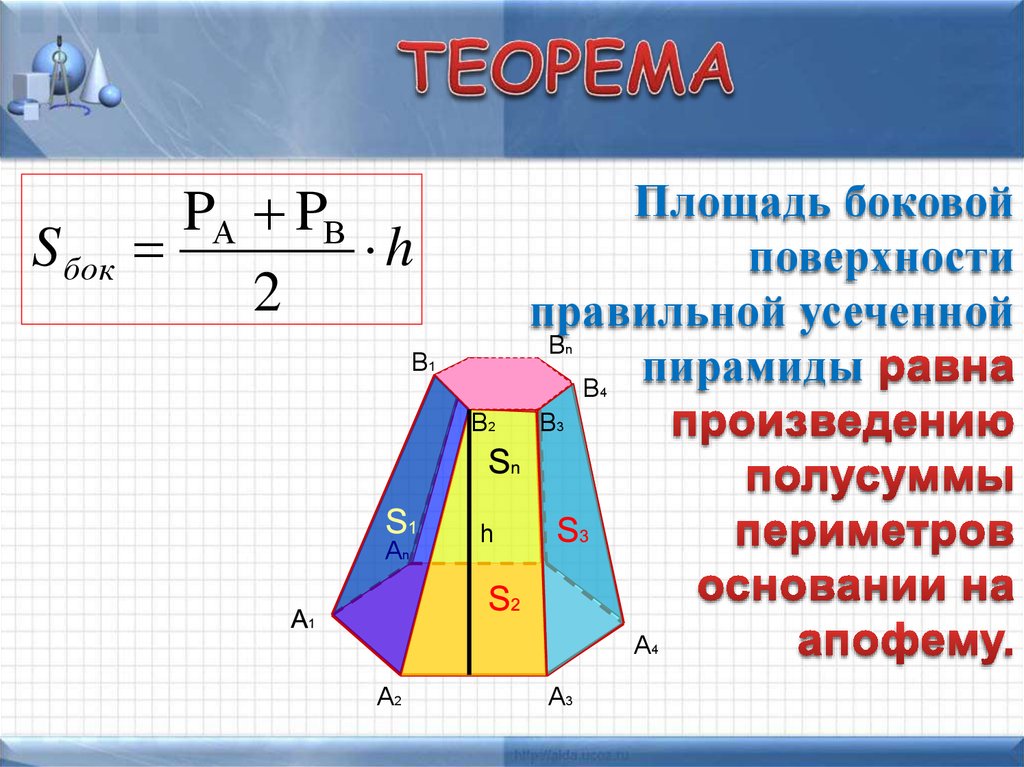
23.

S бок
PА PВ
h
2
Площадь боковой
поверхности
правильной усеченной
В
пирамиды
В
n
В1
4
В2
An
В3
h
A4
A2
A3

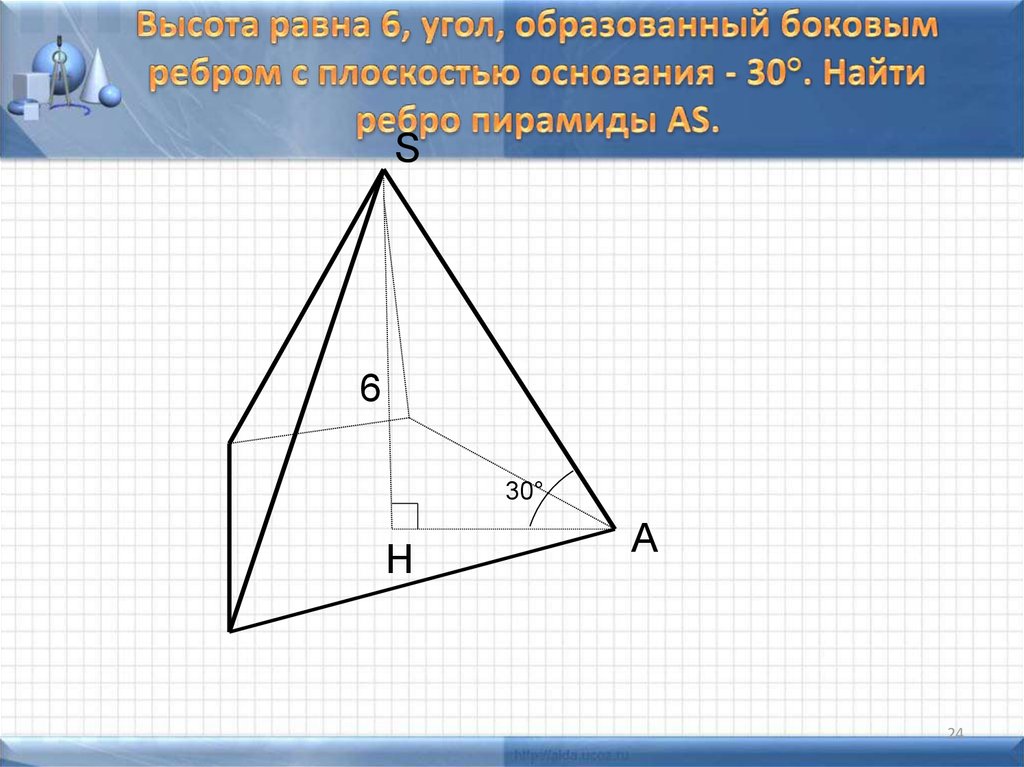
24. Высота равна 6, угол, образованный боковым ребром с плоскостью основания - 30°. Найти ребро пирамиды AS.

S
6
30°
H
A
24

25. ДОМАШНЕЕ ЗАДАНИЕ:

25