Similar presentations:
Площадь параллелограмма, треугольника, трапеции. Геометрия. 8 класс
1. Геометрия 8 класс Решение задач по теме «Площадь параллелограмма, треугольника, трапеции»
2.
Задачи урока:•закрепить навыки вычисления
площади фигур по формуле
•научиться применять изученные
свойства фигур для решения задач
на вычисление площади
•вычисление площадей фигур на
клетчатой бумаге(подготовка к
ГИА )
3.
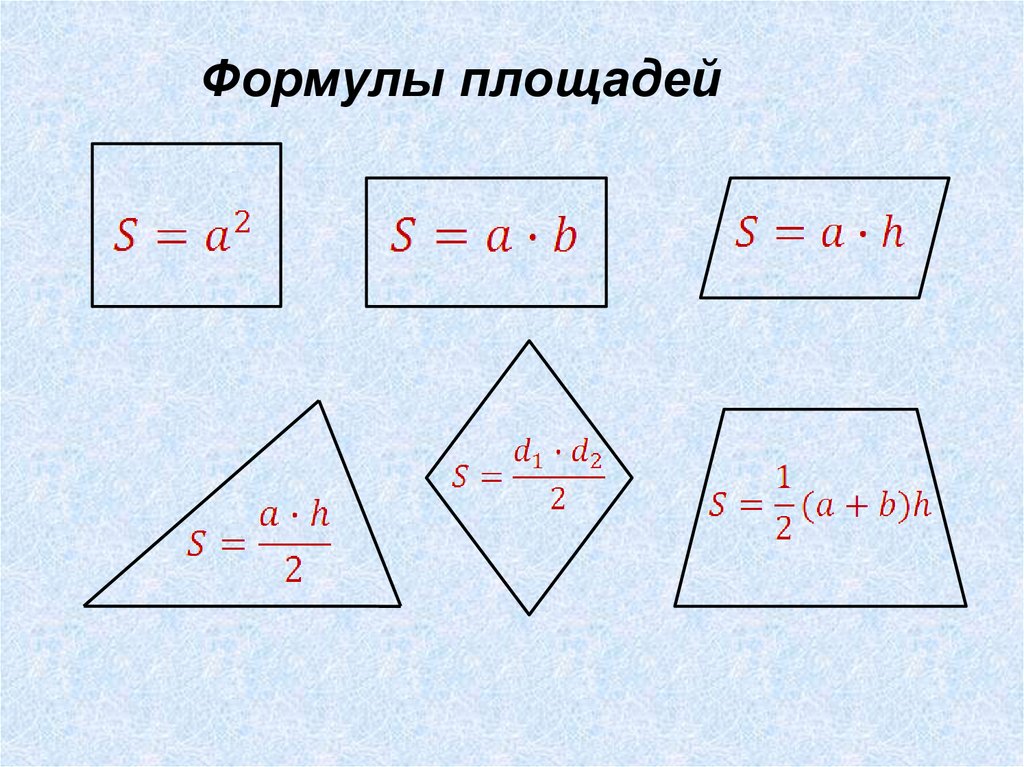
Формулы площадей4.
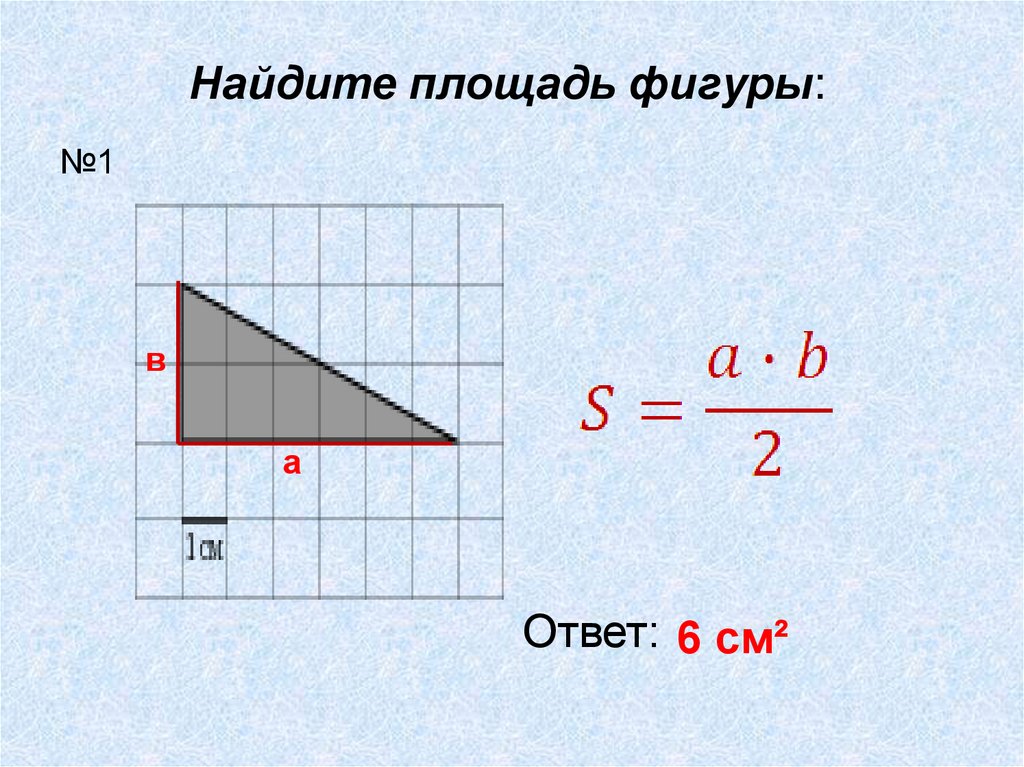
Найдите площадь фигуры:№1
в
а
Ответ: 6 см²
5.
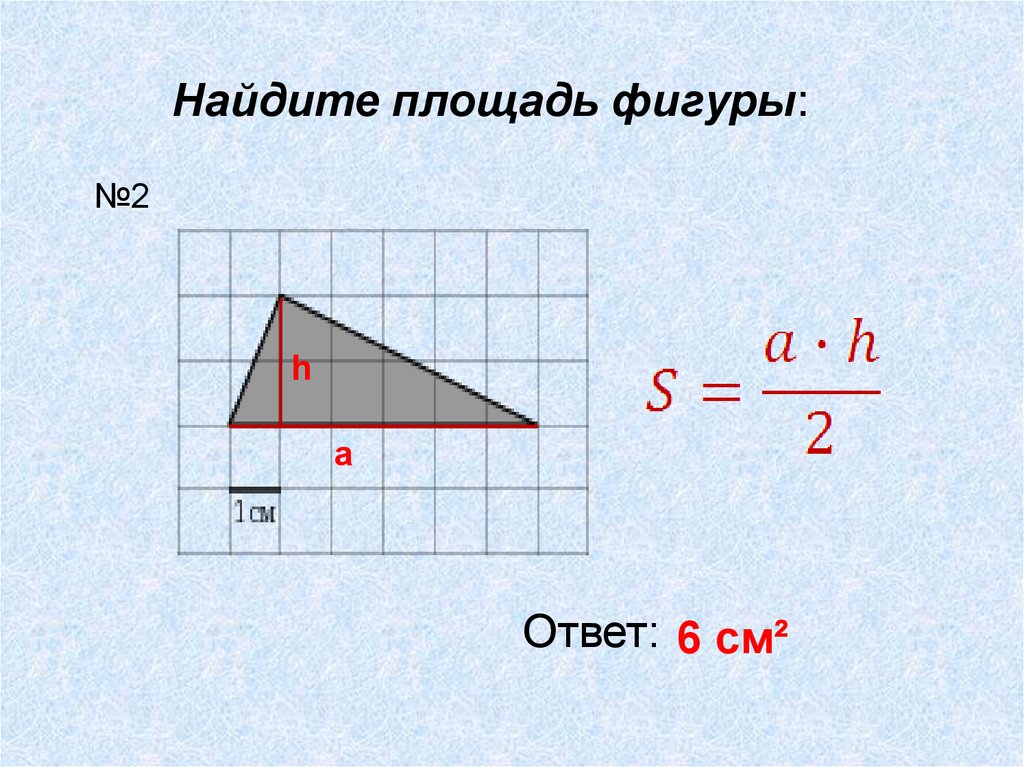
Найдите площадь фигуры:№2
h
а
Ответ: 6 см²
6.
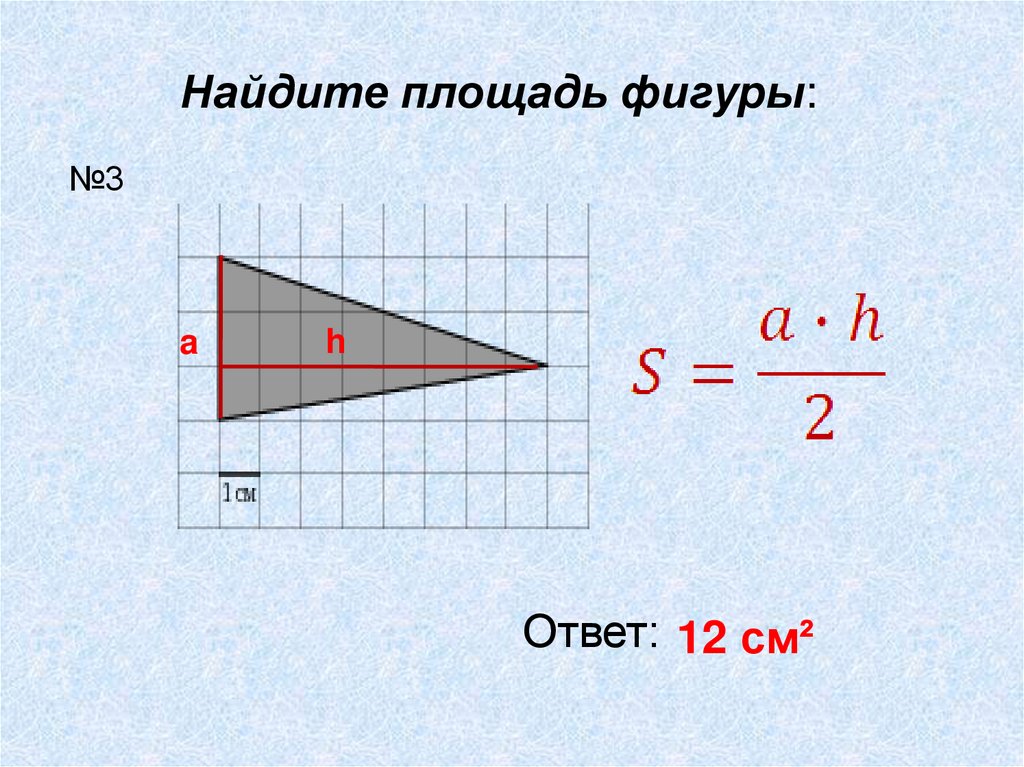
Найдите площадь фигуры:№3
a
h
Ответ: 12 см²
7.
Найдите площадь фигуры:№4
h
a
Ответ: 6 см²
8.
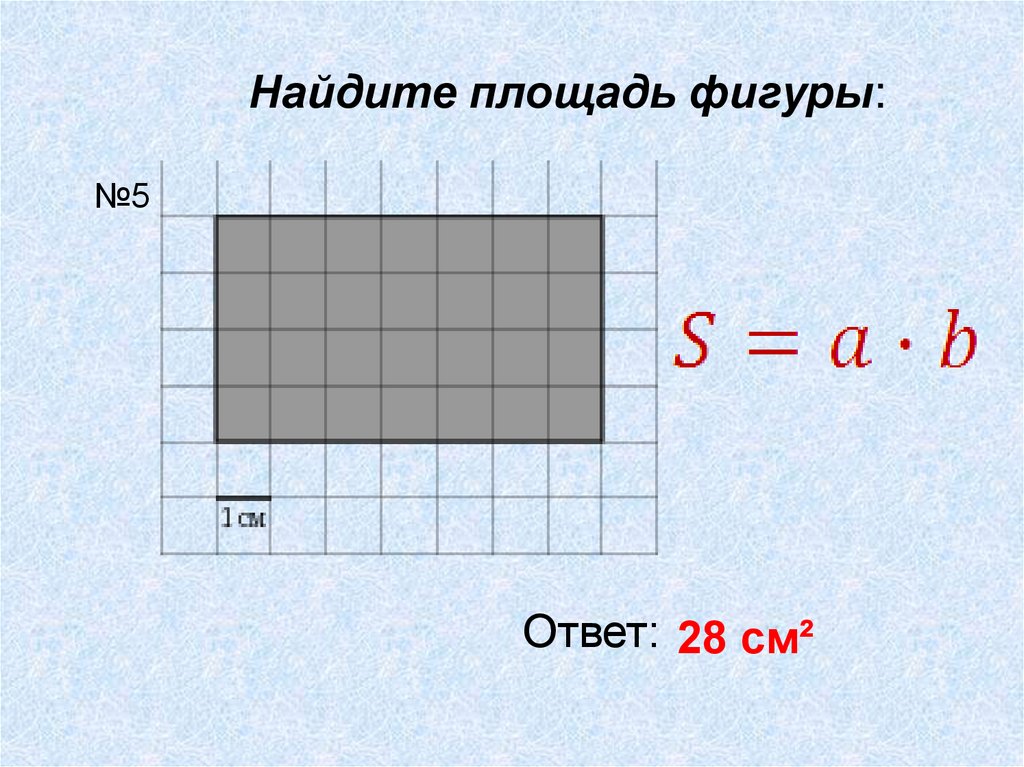
Найдите площадь фигуры:№5
Ответ: 28 см²
9.
Найдите площадь фигуры:№6
d2
1
d1
Ответ: 12 см²
2
10.
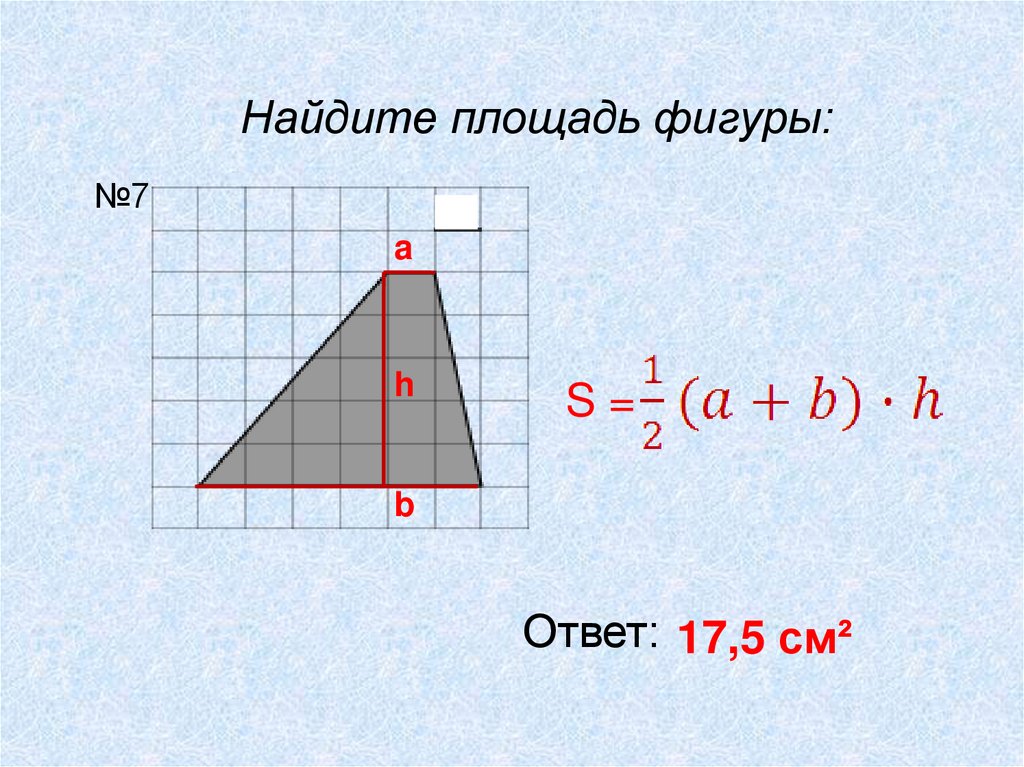
Найдите площадь фигуры:№7
a
h
S=
b
Ответ: 17,5 см²
11.
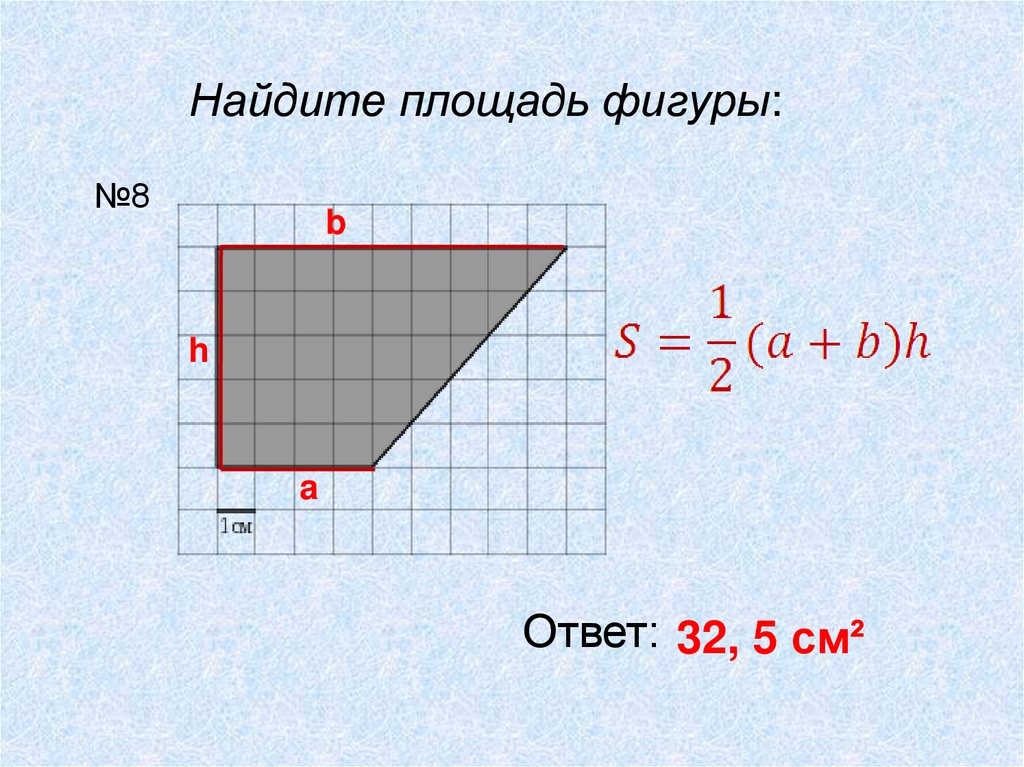
Найдите площадь фигуры:№8
b
h
a
Ответ: 32, 5 см²
12.
Найдите площадь фигуры:№9
h
b
a
Ответ: 15 см²
13.
Найдите площадь фигуры:№10
h
a
Ответ: 12 см²
14.
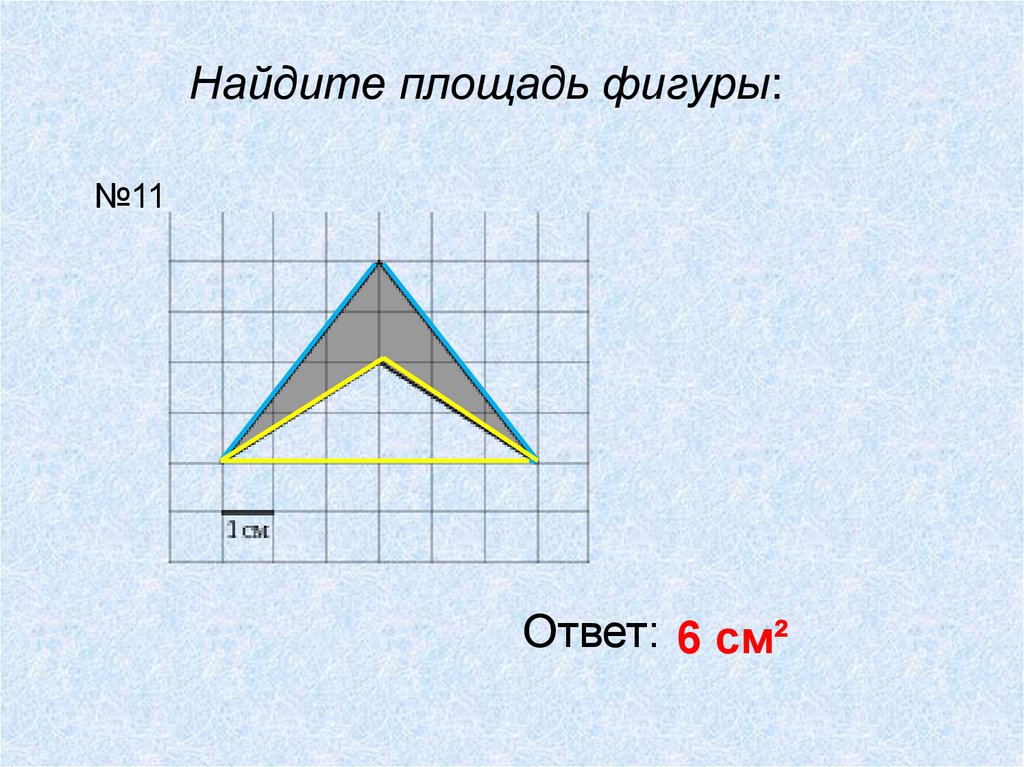
Найдите площадь фигуры:№11
Ответ: 6 см²
15.
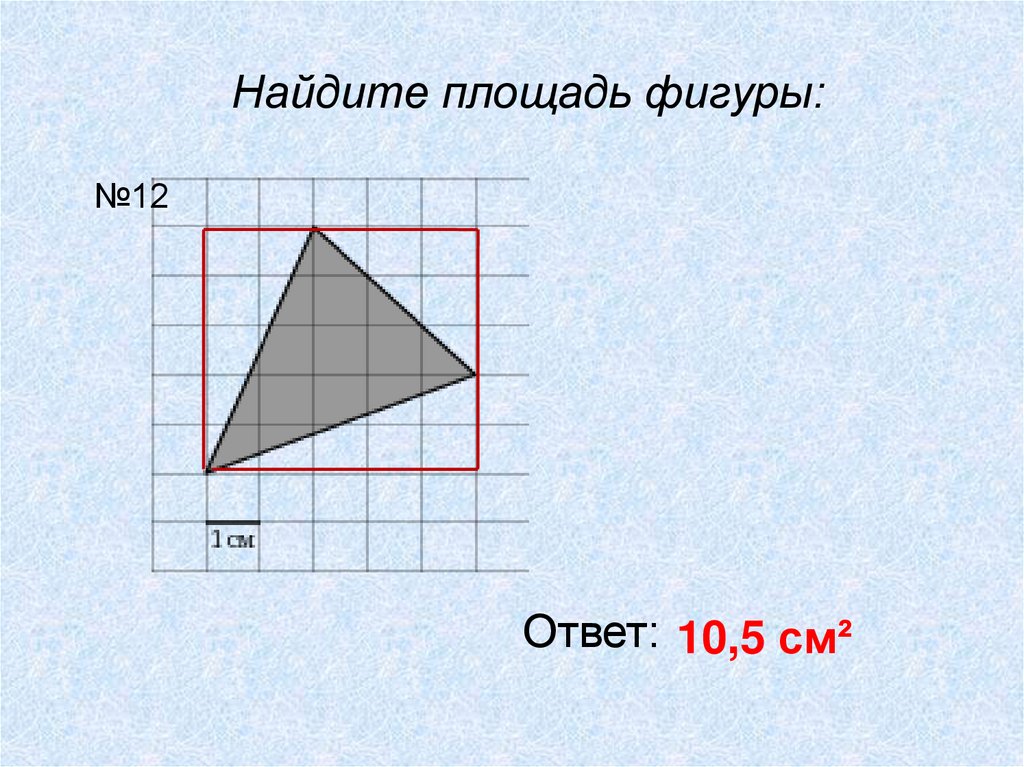
Найдите площадь фигуры:№12
Ответ: 10,5 см²
16.
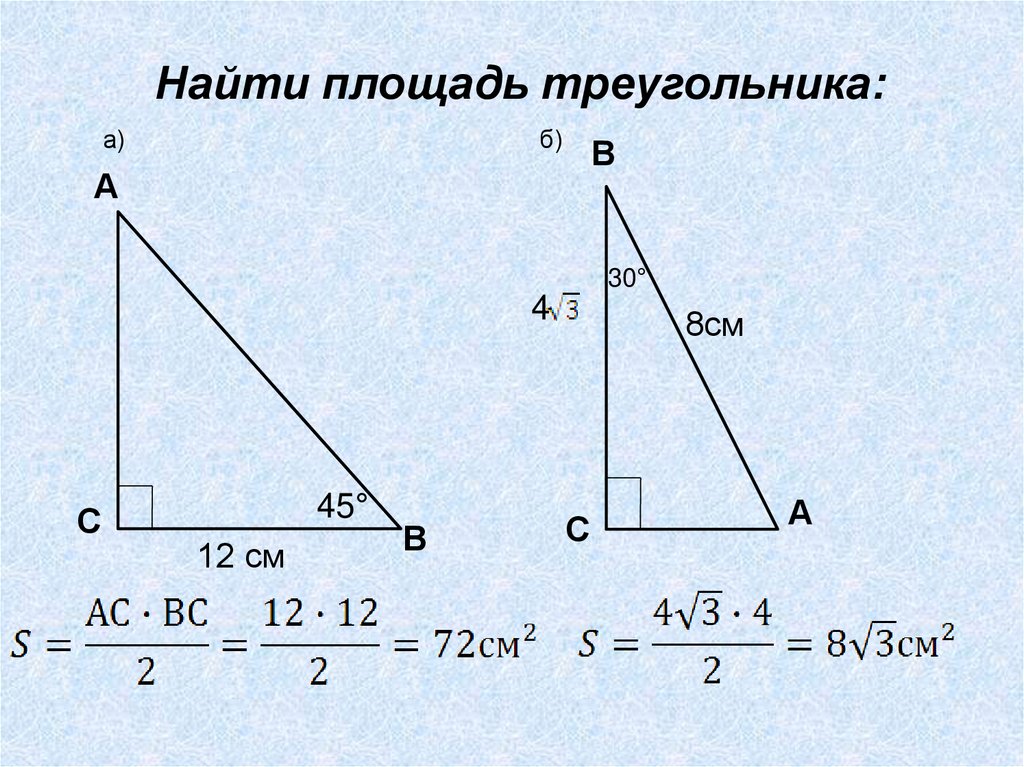
Найти площадь треугольника:а)
б)
В
А
30°
4
С
45°
12 см
В
8см
С
А
17.
1. В треугольнике АВС С = 135 ,АС = 6 дм, высота ВД равна 2 дм. Найти
площадь треугольника АВД.
В
Решение:
АВД- прямоугольный
А
С
Д
ВСД – прямоугольный, ВСД = 180 -135 = 45
СВД =45 ВСД- равнобедренный, СД = ВД =
=2 дм АД = АС + СД = 8 дм
Ответ: 8дм²
18.
№ 463Дано:
Решение:
АВСД - параллелограмм 1. Из вершины В
А
В
проведём высоту на
продолжение стороны
ДС
2. SАВСД = ДС∙ВН
30
Д
С
Н
ВД= 14 см, ДС = 8,1 см
3. ВДН – прямоугольный,
ВДС = 30
ВДС = 30
Найти :
SАВСД
SАВСД = ДС∙ВН =8,1∙ 7 = 56,7 см²
Ответ: 56,7 см²
19.
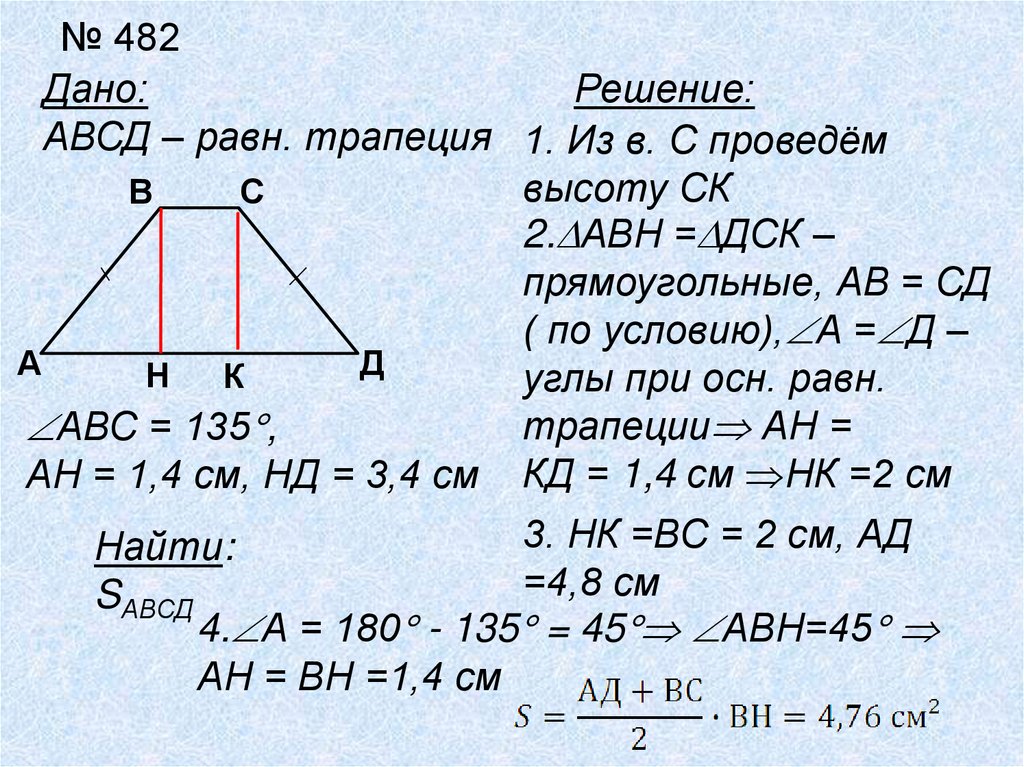
№ 482Дано:
Решение:
АВСД – равн. трапеция 1. Из в. С проведём
высоту СК
В
С
2. АВН = ДСК –
прямоугольные, АВ = СД
( по условию), А = Д –
А
Д
Н
К
углы при осн. равн.
трапеции АН =
АВС = 135 ,
АН = 1,4 см, НД = 3,4 см КД = 1,4 см НК =2 см
3. НК =ВС = 2 см, АД
Найти:
=4,8 см
SАВСД
4. А = 180 - 135 = 45 АВН=45
АН = ВН =1,4 см








 mathematics
mathematics








